挤压辊是高压辊磨机最重要的部件之一。采用圆锥过盈配合的组合辊是目前公认的矿山粉磨工艺最合理的挤压辊结构^[1]。组合辊的工作环境极为复杂, 且承受着巨大的载荷, 因此准确预测、控制和分析组合辊承载能力, 对研发高强度、长寿命及高可靠性的磨辊十分重要。许多学者对组合辊做了大量的实验研究, 如李伟建等^[2]对圆锥面过盈配合联接的静应力计算方法进行了研究, 提出了一种基于平面应变的工程算法; 高航等^[3]在辊面磨损方面通过理论分析和实验研究, 获得了辊面的磨损规律; 刘义等^[4]在组合磨辊强度方面进行了有限元仿真分析, 得出了磨辊工作时的静态压力分布规律。以往的研究多集中于辊面磨损及磨辊强度分析以及结构参数对组合辊转矩承载能力的影响规律, 而针对鼓形误差对组合辊转矩承载能力影响的研究相对较少。准确地估计鼓形误差关系到组合辊扭矩传递的可靠性, 目前组合辊鼓形误差的确定在很大程度上依赖于设计者的经验和应用中的反馈信息, 不同的生产厂家或不同的设计者可能确定不同的鼓形公差, 导致组合辊的承载转矩有较大的差异^{[5, 6]}。

本文以GM1800× 1400高压辊磨机的圆锥过盈配合组合辊为研究对象, 根据高压辊磨机的工作原理, 建立组合辊圆锥过盈联接的几何模型, 得到组合辊承载扭矩的关键结构参数, 在确定过盈量参数范围和选取适当的过盈量基础上, 分析了鼓形误差对组合辊最大承载扭矩的影响, 寻找其对组合辊结合面径向应力的影响, 以及与最大承载扭矩之间的固有规律, 从而为在组合辊的设计中提高过盈连接承载能力和可靠性提供依据。

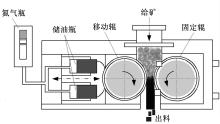
高压辊磨机主要由组合辊、机架、压力提供系统、传动系统、扭转平衡系统、给料系统、电控系统及冷却系统等组成, 其工作原理如图1所示。物料由给料系统产生一定的给料压力(重力或预压螺旋给料机)进入两平行相向旋转的挤压辊之间, 通过挤压辊的连续转动带入辊间, 使其受到50~300 MPa的高压作用后, 物料颗粒相互挤压而破碎成极细的粒度, 以密实的饼料形式从机下挤出, 饼料中不仅含有一定比例的细微成品, 同时非成品颗粒内也形成了大量的微裂纹, 使得在后续的设备破碎粉磨过程中显著地降低能耗^[7]。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 高压辊磨机工作原理图Fig.1 Working principle diagram of high pressure grinding rolls

以GM1400× 800高压辊磨机的组合辊为研究对象, 其主要技术参数指标如下:电机额定功率为500 kW(2× 250 kW), 额定转速为1480 r/min, 额定转矩为3326 Nm; 安全联轴器扭矩为11 200 Nm, 对应组合辊的最大外载扭矩为789 kN· m; 动辊质量为14 000 kg, 正常转速为21 r/min; 油缸推力为463 kN, 预挤压应力为135 MPa。

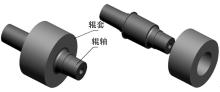
高压辊磨机组合辊主要由辊套、辊轴、合金柱钉及辊面护板等组成, 其三维模型如图2所示, 辊套和辊轴的结构参数见表1, 材料性能参数见表2。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 圆锥过盈配合组合辊三维模型Fig.2 Three-dimensional model of cone- interference-fit combined roller

表1

Table 1

表1(Table 1)

表1 辊套与辊轴的结构参数(圆锥小端) Table 1 Structure parameters of roller sleeve and shaft (small cone end) 零件名称 外径/mm 内径/mm 结合长度/mm 结合面锥度 辊套 1400 700 800 1∶ 50 辊轴 700 160 800 1∶ 50

表1 辊套与辊轴的结构参数(圆锥小端) Table 1 Structure parameters of roller sleeve and shaft (small cone end)

表2

Table 2

表2(Table 2)

表2 辊套与辊轴材料的主要性能参数 Table 2 Main material performance parameters of rollersleeve and shaft 零件名称 材料名称 弹性模量 E/GPa 泊松比 屈服强度 σ /MPa 辊套 34CrMoNi 206 0.30 930 辊轴 45钢 210 0.30 450

表2 辊套与辊轴材料的主要性能参数 Table 2 Main material performance parameters of rollersleeve and shaft

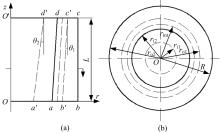
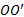
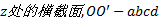
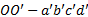
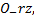
建立圆锥过盈联接组合辊的几何模型, 如图3所示, 图3(a)可视为图3(b)沿轴中心线 剖开的半轴截面, 而图3(b)为图3(a)在轴向 表示辊套, 表示辊轴。由于圆锥过盈联接组合辊为典型的轴对称结构, 所以建立图中所示的柱坐标系 各几何参数的计算式如下:

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 圆锥过盈联接组合辊的几何模型Fig.3 Geometric model of cone-interference-connection combined roller

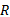
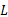
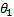
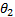
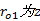
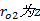
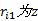
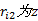
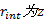
图3与式(1)中各参数含义如下: 为组合辊外半径, mm; 为过盈配合段长度, mm; 为辊套接触面锥角或内锥角; 为辊轴结合面锥角; 处辊轴外半径, mm; 处辊套外半径, mm; 处辊轴内半径, mm; 处辊套内半径, mm; 为过盈量, μ m; 处过盈面半径, mm。

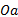
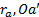
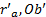
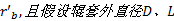
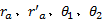
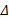
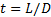
为分析和计算方便, 令 为 为 为 为不变常量, 及 为独立的参变量, 并设长径比 在某一设定范围内取值。

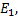
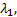
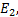
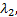
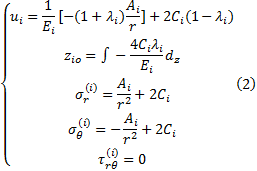
根据圆锥联接的几何模型, 设辊轴材料的弹性模量为 泊松比为 辊套材料的弹性模量为 泊松比为 且假设分析计算时, 辊轴与辊套的变形产生在弹性变形范围内。由此, 可根据轴对称平面应力问题求解方法, 得出辊轴、辊套的位移分量和应力分量表达式为:

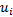
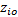
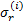
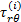
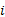
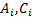
式中: 为径向位移, mm; 为轴向位移, mm; 为径向应力, MPa; 为周向应力, MPa; 为剪切应力, MPa; 取值为1时, 表示辊轴, 为2时表示辊套; 为待定系数, 根据辊轴、辊套的边界条件确定。

式(2)的边界条件为:

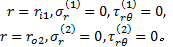
辊轴、辊套结合面接触处径向应力值相等, 即:

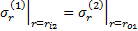
将式(2)中应力分量式代入上面边界条件中可得:

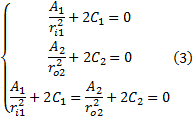
辊轴、辊套结合面接触处的径向位移满足:

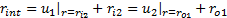
根据式(2)中的径向位移计算式, 上式可改写为:

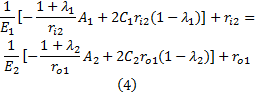
联立式(3)(4)可求解4个系数的值:

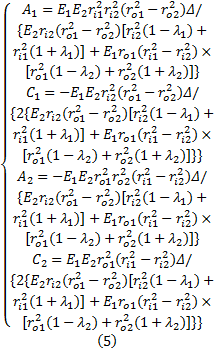
式中: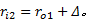

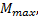
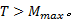
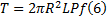
根据高压辊磨机的工作原理可知:组合辊的圆锥过盈联接主要用以承载传递扭矩, 设安全联轴器所承载最大转矩为 则应保证在此转矩下辊轴与辊套结合面上相对应的接触对不产生周向滑移, 即组合辊的承载扭矩大于安全联轴器扭矩,

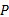
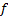
式中: 为结合面压力; 为结合面摩擦因数。

将式(3)(4)(5)代入式(6)可得:

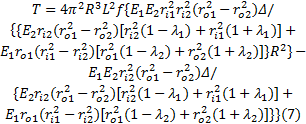
由式(7)可知, 组合辊的扭矩承载能力与过盈量、结合面长度、结合面半径、组合辊外径、辊轴内径以及结合面锥度等关键结构参数密切相关。

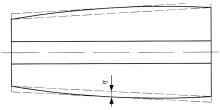
圆锥过盈联接组合辊是利用辊轴与辊套的过盈配合在结合面上产生阻碍两者间相互滑动的正压力, 使得辊套与辊轴相互抱紧, 借助摩擦力矩实现传递扭矩的目的^{[8, 9]}。鼓形误差是指组合辊辊轴或辊套的结合面相对于理论轮廓的凸起量, 定义如下:包容被测轮廓的两同心轴圆锥面的最小距离, 辊轴鼓形误差的定义如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 辊轴鼓形误差的定义Fig.4 Definiton of drum-shaped error of roller shaft

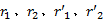
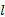
根据图4可知:组合辊辊轴和辊套的鼓形误差由包容圆锥组合辊轮廓的两圆锥的大小端圆半径 和圆锥轴线距离 确定。根据上述定义, 可建立圆锥组合辊鼓形误差的数学模型:

式中: 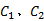为常数。

根据组合辊的工作原理, 由式(6)可得辊轴与辊套间的最小正压力为:

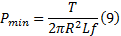
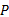
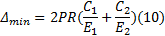
根据弹性力学有关厚壁圆筒的计算理论, 径向压力为 时的过盈连接传递载荷所需的最小过盈量应为:

所以配合面的承载扭矩 为:

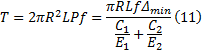
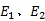
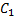
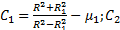
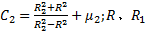
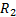
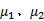
式中: 分别为辊芯与辊套材料的弹性模量; 为辊芯的刚性系数, 为辊套的刚性系数, 和 分别为配合面处半径、辊芯内径和辊套外径; 分别为辊芯与辊套材料的泊松比。

由式(11)可知, 组合辊正常工作所需的摩擦因数值为:

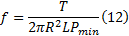
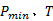
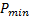
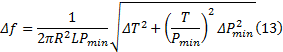
由式(12)可知:辊轴与辊套结合面间摩擦因数的计算准确值取决于 本身的计算精度。由于组合辊结构尺寸误差可以控制到很小, 而且可通过测量手段加以控制, 因此忽略不计。由多元函数的全微分理论可知, 当 、 的测量精度在同一等级时, 结合面间的摩擦因数可按误差绝对值的大小来评定:

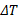
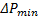
式中: 为外载扭矩误差的绝对值; 为结合面间正压力的误差绝对值; 为结合面间摩擦因数误差的绝对值。

影响组合辊辊轴辊套间结合面摩擦因数的因素有 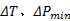误差项, 其中 可根据高压辊磨机工作时的载荷情况及测量仪器确定, 但对于圆锥过盈联接的组合辊辊轴与辊套结合面正压力准确值很难测量, 通常采用计算方法获得。又因为结合面间正压力与辊轴与辊套的过盈量有关, 而实际的过盈量除了与配合处尺寸有关外, 还与结合面的形状误差有较大关系。由此可推得, 结合面间的接触正压力是影响摩擦因数准确程度的主要因素。

根据拉美公式(Lame), 辊轴与辊套间的接触正压力表示为:

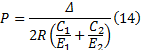
由式(14)可知:结合面间的正压力的误差取决于过盈量的误差和结合面间的尺寸精度, 通常情况下, 结合面间的尺寸精度保证其误差很小, 故而对结合面间正压力的影响可忽略不计, 因此结合面间的正压力绝对误差为:

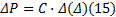
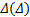
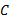
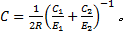
式中: 为过盈量误差; 为常数,

组合辊辊轴与辊套的形状误差引起了过盈量在配合表面纵向和横向的变化, 从而造成结合面间的正压力在整个结合表面的误差不等, 导致了结合面间摩擦因数的变化。因此, 鼓形误差的存在改变了结合面间的摩擦因数, 也改变了辊轴和辊套间的应力分布状况, 从而影响了组合辊辊轴与辊套间的扭矩承载能力。

在分析鼓形误差对组合辊扭矩承载能力的影响之前, 需确定过盈量 参数值范围, 选取适当的过盈量。由高压辊磨机组合辊的工作原理和式(7)可知, 组合辊辊芯与辊套过盈装配所需的过盈量, 应满足的基本要求是能够传递挤压扭矩载荷。为了保证过盈连接传递扭矩的可靠性, 就要求配合面处有较大的径向压力, 而较大的径向压力要求过盈量尽可能取大些。但过大的过盈量可能在配合处产生超过强度条件所允许的应力, 所以在满足基本要求的前提下, 过盈量应尽可能取小些^[10]。图5给出了GM1400× 800高压辊磨机组合辊结合面半径 为350 mm、摩擦因数为0.12时组合辊的承载扭矩随过盈量增加的变化规律。

图5

Fig.5

	Figure Option ViewDownloadNew Window
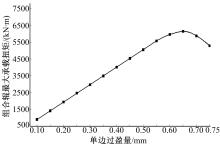	图5 单边过盈量对组合辊承载扭矩的影响Fig.5 Influence of unilateral interference quantity on combined roller bearing torque

由图5可知:过盈量对组合辊结合面径向应力分布和承载扭矩影响较大, 单边过盈量小于0.60 mm时, 组合辊最大承载扭矩随过盈量增加呈线性增大; 单边过盈量大于0.60 mm后, 组合辊最大承载扭矩随过盈量增加而增大的趋势逐渐减小; 单边过盈量等于0.68 mm时, 最大承载扭矩达到最大值6129 kN· m; 此后, 组合辊承载扭矩随过盈量的增加而减小, 且减小趋势逐渐增大。综合分析可知, 单边过盈量的取值范围为0.30~0.55 mm, 所以后续的影响分析中, 过盈量 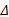一般取0.45 mm。

以GM1400× 800高压辊磨机组合辊结构参数为参照, 假设组合辊辊套内孔面无形位误差, 而辊轴外表面在配合处的中心存在η =0.07 mm的鼓形误差, 如图4所示, 对该情况进行仿真计算。图6为辊轴外表面存在鼓形形状误差的条件下组合辊过盈配合中辊套内表面径向应力分布曲线图。图中曲线a为理想状况下无形位公差的应力分布; 曲线b为过盈量Δ =0.45时存在η =0.07 mm鼓形误差的应力分布情况; 曲线c为过盈量Δ =0.40时存在η =0.07 mm鼓形误差的应力分布情况。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 不同过盈量时鼓形误差对组合辊辊套内表面径向应力的影响Fig.6 Influence of drum-shaped error on radial stress of combined roller sleeve contact surface when interference quantity is different

由图6可以得出, 存在鼓形误差时, 组合辊辊套内表面的径向接触应力发生了改变。曲线c与曲线a相比, 在配合段中心处, 径向应力增大, 两端的集中应力减小, 改善了应力集中现象, 使得接触应力在整个配合段分布趋于均匀。由此可得出结论:存在适当的鼓形误差有利于减小组合辊过盈联接在配合段两端存在的应力集中现象。

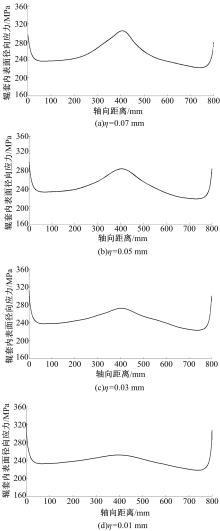
当过盈量Δ =0.45 mm、鼓形误差η 分别取0.07、0.05、0.03、0.01 mm时, 组合辊过盈配合中辊套内表面径向应力分布曲线如图7所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 同一过盈量时鼓形误差对组合辊辊套内表面径向应力的影响Fig.7 Influence of drum-shaped error on radial stress of combined roller sleeve contact surface when interference quantity is identical

由图7可知:鼓形误差越大, 组合辊出现鼓形误差配合处的径向应力越大, 两端的集中应力越小。GM1400× 800高压辊磨机组合辊的鼓形误差η =0.07 mm时, 结合面间的最大径向应力出现在配合段的中点(鼓形误差最大值处), P_max=308 MPa, 径向应力平均值P=266 MPa; 鼓形误差η =0.03 mm时, 结合面间的最大径向应力出现在圆锥小端端点处, P_max=312 MPa, 径向平均应力值P=255 MPa; 鼓形误差η =0.01 mm时, 结合面间的最大径向应力出现在圆锥小端端点处, P_max=324 MPa, 径向平均应力值P=249 MPa; 无鼓形误差的理想状况, 结合面间的最大径向应力出现在圆锥小端端点处, P_max=329 MPa, 此时径向平均应力值P=242 MPa。综上可以得出, 适当的鼓形误差不仅能减小出现在结合面两端的应力集中, 使得结合面径向应力分布更均匀, 而且径向平均应力值得到了提高。

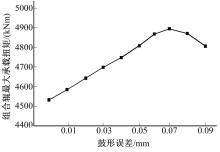
鼓形误差对GM1400× 800高压辊磨机组合辊承载扭矩的影响如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 鼓形误差对组合辊承载扭矩的影响Fig.8 Influence of drum-shaped error on combined roller bearing torque

由图8可知:组合辊配合段中点存在的鼓形误差η 大于0.02 mm时, 最大承载扭矩明显增大, η =0.07 mm时, 达到最大值, 此后, 随着鼓形误差的增大, 其承载扭矩逐渐减小。

综上分析可知:为了减小组合辊结合面两端的应力集中, GM1400× 800高压辊磨机组合辊的鼓形误差η 的最佳范围应控制在0.03~0.07 mm。

建立了组合辊圆锥过盈联接的几何模型, 以GM1400× 800高压辊磨机组合辊为研究对象, 得到组合辊承载扭矩的关键结构参数, 在确定过盈量参数范围(0.30~0.55 mm)以及选取适当的过盈量(Δ =0.45 mm)的基础上, 分析了组合辊接触表面鼓形误差对组合辊承载扭矩的影响。由于鼓形误差的存在, 导致结合面间的正压力分布不均, 从而影响了结合面间的摩擦因数, 进一步影响了组合辊承载扭矩的能力。利用有限元分析软件ANSYS分析了鼓形误差对GM1400× 800高压辊磨机组合辊承载扭矩的影响, 得到如下结论:适当的鼓形误差能减小组合辊结合面两端的应力集中, 使得结合面径向应力分布更均匀, 径向平均应力值得到提高。当过盈量Δ =0.45 mm, 鼓形误差η 小于0.07 mm时, 最大承载扭矩随鼓形误差单调递增, η =0.07 mm时, 达到最大值, 此后, 随着鼓形误差的增大, 其承载扭矩逐渐减小。因此为了减小组合辊结合面两端的应力集中, 组合辊的鼓形误差η 的最佳范围应控制在0.03~0.07 mm内。除了鼓形误差, 还有圆度误差、锥度误差等对高压辊磨机组合辊承载扭矩的影响, 还有待进一步研究。