孟广伟(1959-),男,教授,博士生导师.研究方向:疲劳与断裂.E-mail:mgw@jlu.edu.cn
针对材料的非均质、多尺度问题,提出了光滑多尺度有限元法。将该方法用于求解裂隙介质的渗流问题,采用双重介质模型进行模拟。利用初始时刻的全局细尺度解确定边界条件构造多尺度基函数,从而将局部非均质信息和孔隙-裂隙流体流动耦合的全局信息同时反映到多尺度基函数上,由此在粗尺度上获得精确解。光滑多尺度有限元将应变光滑技术引入到传统多尺度有限元中,简化了宏观矩阵的组装,克服了常规有限元计算刚度过硬的缺陷。计算结果表明:光滑多尺度有限元的结果与常规有限元的细尺度解有很好的一致性,并且比传统多尺度有限元计算效率高、精度好。
Smoothed Multiscale Finite Element Method (SMsFEM) is proposed to solve the problems associated with heterogeneous and multiscale materials. SMsFEM is used to study the fliud flow in fractured madia with a dual porosity model. Using the global fine-scale solution at initial time to determine the boundary conditions of the basis function, local information of material heterogeneity and coupled global information, such as fluid flow in porous and fractured media, are simultaneously reflected in the multiscale finite element basis functions. As a result, an accurate solution can be achieved in the coarse scale. SMsFEM introduces the strain smoothing technique into conventional Multiscale Finite Element Method (MsFEM), therefore, simplifies the assembly of the macro matrix and overcomes the overly-stiff phenomenon existing in the traditional finite element method. Simulation results indicate that the proposed SMsFEM is highly consistent with the fine-scale solutions from standard finite element method. It is also demonstrated that SMsFEM has better efficiency and accuracy than MsFEM.
裂隙介质广泛存在于地层结构中, 其内部裂隙结构复杂、分布随机、裂隙长度同基质材料差异很大, 具有强烈非均质和明显多尺度特征。为了解决这类问题, 各种多尺度、升尺度算法[1, 2]被相继提出, 其中多尺度有限元法(MsFEM)[3, 4]的应用最为广泛。近两年, 裂隙介质渗流的多尺度分析成为力学界的研究热点之一。Zhang等[5]提出了基于离散裂隙模型的多尺度有限元法; Hajibeygi等[6]提出了基于分层断裂模型的迭代多尺度有限体积法。由于离散裂隙模型和分层断裂模型的裂隙特征参数获取困难, 对于裂隙较多的地层计算量巨大, 为此, 本文采用双重介质模型求解裂隙介质的渗流问题, 并将多尺度有限元法引入到该模型中。
传统多尺度有限元法求解实际问题时多尺度基函数的构造和组装程序编写复杂, 运算耗费大量时间。为了解决这一问题, 本文对传统多尺度有限元法进行了改进, 将应变光滑技术引入到多尺度有限元法中, 提出了光滑多尺度有限元法(SMsFEM), 并编写了计算程序, 通过求解裂隙岩体渗流问题验证了该算法的正确性和高效性。
双重介质模型最初由前苏联学者Barenblatt[7]于1960年提出, 是目前在水文地质领域应用最广的裂隙介质渗流模型。该模型将裂隙和孔隙系统地处理为两个平行的连续体, 两者之间存在水交换, 其值取决于两者的水头差。控制方程如下:
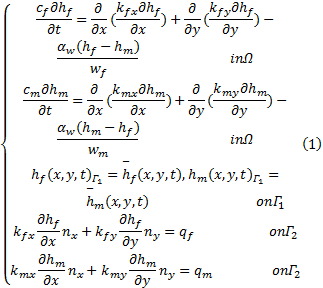
式中:下标f表示裂隙; m表示孔隙; Ω 为求解域; h为压力水头; c为贮水系数; k为渗透系数, 一般是随机非均质的; α w 为一阶质量传递系数, w为孔隙度; Γ 1为已知水头边界; 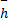
在双重介质模型中, 裂隙和孔隙的渗透系数均存在强烈的非均质性, 并且裂隙和孔隙内流体的流动存在耦合关系。本文分别构建裂隙水头和孔隙水头的多尺度基函数, 使其满足各自的椭圆微分方程。采用初始时刻的全局细尺度解确定多尺度基函数的边界条件, 使基函数在捕捉局部非均质性的同时可以捕捉到裂隙和孔隙内流体流动的耦合信息。并采用应变光滑技术构造宏观矩阵, 进一步提高算法的精度和效率。
基于双重介质模型对裂隙介质渗流进行分析时选择裂隙水头hf和孔隙水头hm作为基本变量, 采用加权残余法推导其多尺度有限元求解列式, 在每个单元内hf和hm为:
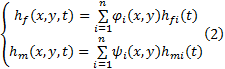
式中: 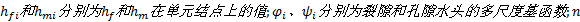
将权函数取为对应的多尺度基函数, 由Green公式及Galerkin法, 双重介质模型的多尺度有限元列式为:
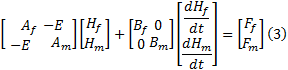
式中: 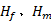
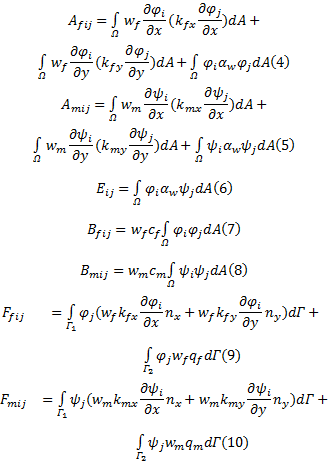
式(3)可表示为:
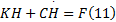
矩阵 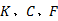
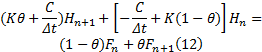
式中:Δ t为时间步长; 带下标n+1、n的矩阵为tn+1 、tn 时刻的状态矩阵; θ 为插值参数。
多尺度有限元法的关键是构造可以反映材料微观结构信息的多尺度基函数。多尺度基函数是满足给定边界条件的简化控制方程的解。因此, 对于双重介质模型, 裂隙和孔隙的多尺度基函数满足:
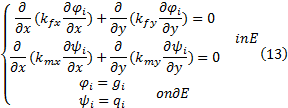
式中: 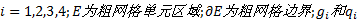
本文采用有限全局信息构造多尺度基函数的边界条件[8], 将局部的非均质信息和孔隙-裂隙流体流动相互耦合的全局信息同时反映到多尺度基函数上。
采用有限全局信息构造多尺度基函数的主要思想是利用初始时刻方程的细尺度解确定多尺度基函数的边界条件。将方程(12)在初始时刻细尺度的值表示为 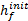
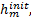
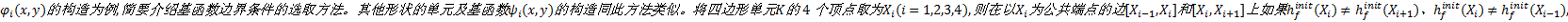
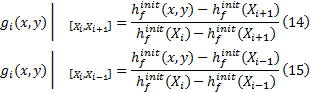
如果 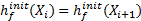
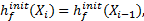
应变光滑技术最初由Chen[9]在无网格伽辽金法中提出, 为了消除固有结点积分中弱式的欠积分造成的不稳定现象。2007年, Liu[10]将该技术引入到有限元中, 提出了光滑有限元法(Smoothed finite element method, SFEM)。SFEM[11]采用应变光滑技术构建应变场, 计算应变能, 利用光滑伽辽金弱形式对系统方程进行离散。由此构造的应变场只需要在光滑区域边界上进行简单的线积分, 并且不需要整体坐标同局部坐标的转换, 在提高了计算效率的同时使域的离散更加灵活。
光滑应变场采用公式(16)构造:
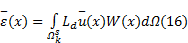
式中: 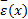
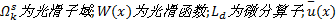
取 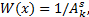
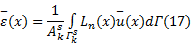
式中: 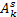
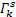
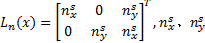
在光滑子域内的连续位移场函数为:
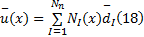
式中: 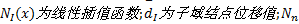
将式(18)代入式(17), 则光滑应变场可表示为:
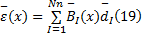
式中: 
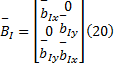
矩阵中各元素为:
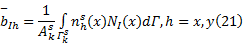
采用单高斯点对式(21)进行求解, 得:
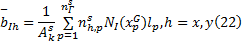
式中: 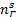
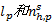
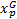
将应变光滑技术引入到多尺度有限元法中对宏观矩阵进行组装时, 首先选取细网格单元作为光滑子单元, 子单元结点处的基函数值取为该点的多尺度基函数值。通过取平均值得到光滑区域各边中点(高斯点)处的基函数值。然后, 引入应变光滑技术, 构造光滑水头梯度矩阵。最后, 利用光滑伽辽金弱形式对裂隙介质渗流控制方程进行离散, 计算各矩阵的值。下面以矩阵 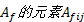
将 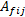
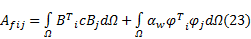
式中: 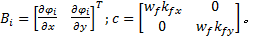
将问题域划分为若干光滑子区域后, 采用应变光滑技术, 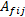
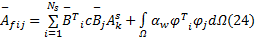
式中: 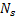
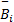
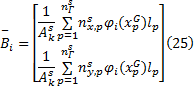
式(3)中其他矩阵的构造同 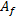
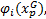
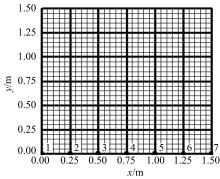
选取1.5 m× 1.5 m的裂隙岩体作为研究对象进行分析。首先对模型进行空间离散, 将研究区域划分为6× 6的粗网格和30× 30的细网格, 如图1所示。在每个细网格内, 材料参数是均质的, 以便使用常规有限元法在细网格上进行求解。
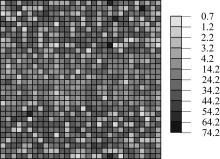
为了体现裂隙和孔隙介质的非均质性, 将细网格单元的渗透率参数取为不同值, 图2为裂隙介质的渗透率分布图。孔隙的渗透率取为坐标 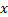
分别采用光滑多尺度有限元(SMsFEM)、多尺度有限元(MsFEM)和在细网格上的常规有限元(FEM-F)三种算法求解裂隙介质渗流问题, 对计算的结果和耗时进行对比分析。
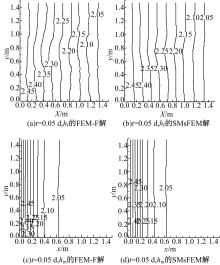
选取0.05 d的裂隙和孔隙水头的SMsFEM和FEM-F的结果绘制等值线图进行比较, 如图3所示。从图中可以看出:采用常规有限元在细网格上的计算结果与光滑多尺度有限元在粗网格上的计算结果基本一致。可见, 采用有限全局信息的光滑多尺度有限元法可以有效地捕捉材料的微观信息, 在较粗的网格上得到较精确的结果, 验证了SMsFEM的正确性。
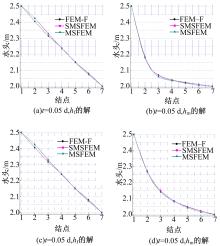
图4为SMsFEM、MsFEM和FEM-F三种算法在t=0.05 d和t=0.1 d, 1~7点处(如图1所示)求解的裂隙及孔隙水头值对比曲线。从图中可以看出:SMsFEM和MsFEM的值与FEM-F的值吻合得很好, 其中SMsFEM的结果更接近FEM-F的值。主要是由于SMsFEM算法在组装宏观矩阵时将面积分转化为线积分, 克服了传统有限元计算刚度过硬的缺点, 由此提高了计算结果的精度。
用SMsFEM、MsFEM两种算法计算宏观矩阵时计算耗时分别为14.3512 s和19.1325 s, 采用SMsFEM的计算时间比MsFEM快25%。对于网格数目众多的实际工程问题, 此种优势会更加明显。可见, 将应变光滑技术引入到多尺度有限元中可以有效提高计算效率。
表1为SMsFEM、FEM两种算法的计算耗时对比。通过对表中数据进行处理可以得到, 在t=0.5 d时SMsFEM的计算耗时仅为FEM-F的17.5%; 在t=2.5 d时SMsFEM的计算耗时仅为FEM-F的7.4%; 在t=5 d时SMsFEM的计算耗时仅为FEM-F的6.1%。可见, 采用SMsFEM算法在粗网格上计算非均质裂隙介质的渗流问题大大节省了计算时间, 并且随着运算时间的增加, SMsFEM同FEM-F计算耗时的比值越来越小, SMsFEM算法的优势越来越明显。
| 表1 SMsFEM和FEM计算耗时对比 Table 1 Comparison of CPU time between SMsFEM and FEM |
(1)采用光滑多尺度有限元法求解的结果同有限元法在细网格上求解的结果基本一致, 并且大大节省了计算的时间。
(2)本文提出的光滑多尺度有限元法比常规的多尺度有限元法计算耗时更少, 精度更高。
(3)利用有限全局信息构造的多尺度基函数可以更好地捕捉材料的非均质性及裂隙和孔隙介质内流体流动的耦合关系。
本文提出的光滑多尺度有限元法可以解决几乎所有常规多尺度有限元法可以解决的问题。比如:多孔介质内单相流和多相流的流动问题、复合材料的热传导问题等, 可见该方法具有广阔的应用前景。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|