张锐(1975-),男,教授,博士.研究方向:松软地面仿生行走及数值计算.E-mail:zhangrui@jlu.edu.cn
采用逆向工程技术,完成了鸵鸟足底曲面三维重构和分区,基于离散元法和有限元法,进行了鸵鸟足底曲面/沙土相互作用数值模拟。鸵鸟足底曲面下沙土颗粒流动程度沿足宽方向大于沿足长方向,表明鸵鸟足底曲面形貌更好地减缓了鸵鸟足在沙地上的前行滑移程度。在鸵鸟足多曲面结合形貌中,第Ⅲ趾底中间凹槽面固沙限流效果最好,此区域的沙土颗粒群受力呈现网格状稳态紧固分布。鸵鸟足第Ⅲ趾底中间凹槽面数学模型的建立,为鸵鸟足底曲面仿生设计提供了重要理论依据。
3D model reconstruction and partition of the plantar surface of ostrich didactyl foot were achieved using reverse engineering. Discrete element method and finite element method were employed to simulate the interactions between the plantar surface of ostrich didactyl foot and sand. It was shown that the flowing extent of sand particles under the plantar surface along the foot breadth direction was greater than that along the foot length direction. This may indicate that the plantar surface morphology of ostrich foot can preferably retard the slippage during ostrich foot moving ahead on sand. Within the plantar surface of ostrich foot, the middle groove in the third toe plantar surface has most obvious effect of sand flow fixation, under which the forces on the sand particle groups present the grid-patterned stable tight distribution. A mathematical model of the middle groove in the third toe plantar surface was established, which may provide theoretical reference for bionic design of the plantar surface of ostrich foot.
地球的沙漠和戈壁以及深空的月球和火星, 它们的共同特点是具有松散介质工作环境。作为在松散介质工作环境中完成探测、运输及开采任务的重要装备, 车辆(或机器人)的基本功能是松散介质表面的通过能力。车辆(或机器人)的通过性能在很大程度上取决于直接与地面发生作用的行走机构, 尤其在深空探测中, 行走机构在月球和火星表面松散介质工作环境中的通过性直接关系到太空车任务的成败。美国“ 勇气” 号火星车就是由于受到火星表面松软地面环境的影响出现严重沉陷不能脱身, 最终被迫终止探测任务[1]。因此, 松软地面行走机构研究已经成为地(月)面车辆系统领域的热点问题之一[2]。
研究人员通过分析松软地面环境生存动物优异运动性能, 采用工程仿生学技术, 设计和优化松软地面行走机构, 以提高其沙地环境通过性能, 取得了一系列创新研究成果[3, 4]。王志浩等[5, 6, 7]根据驼足结构及其与沙地的独特作用方式, 研制仿驼步行足和仿驼足轮胎, 前者可以限沙流动和提高承载, 后者具有弹性缓冲、增面固沙及倾斜蹬沙作用。Daniel等[8, 9]根据沙漠蜥蜴和蟑螂的四肢腾空及与沙地接触时的速度变化, 设计了SandBot“ 六肢” 机器人, 使运行速度至少是美国宇航局火星探测器行进速度的15倍。作为典型的沙地环境生存动物之一, 鸵鸟在沙漠环境中具有高速机动的通过性能, 研究鸵鸟关键触沙部位的越沙机制, 将为松散介质工作环境中车辆(或机器人)行走机构的仿生设计提供重要理论依据和全新研究思路。
鸵鸟原产于非洲沙漠地带, 属于平胸类鸟, 不会飞翔, 但具有沙地环境中超强奔跑能力和持久耐力, 持续奔跑速度约50~60 km/h, 冲刺速度超过70 km/h, 是陆地上(尤其是沙地环境)奔跑速度最快的两条腿动物[10]。鸵鸟优异的越沙性能是身体结构、腿、足及运动形态等多方面共同作用的结果[11, 12, 13, 14]。其中, 鸵鸟二趾足是鸵鸟奔跑的唯一触沙部位, 在鸵鸟高速持久奔跑中发挥着极其重要的作用[15, 16, 17, 18]。鸵鸟二趾足长期与沙土直接接触, 经过进化优化, 足底形成了能固沙、限流、防滑移、高效越沙的特殊曲面形态。因此, 分析鸵鸟二趾足底曲面与沙土相互作用关系, 研究鸵鸟足底曲面形态的高效越沙机制, 不仅有助于探究鸵鸟优越的越沙运动性能机理, 而且为鸵鸟足底曲面的工程仿生学应用提供了重要的理论和技术基础。
本文采用逆向工程技术, 重构了鸵鸟足底曲面三维模型, 运用离散元软件EDEM, 并结合有限元软件对鸵鸟二趾足底曲面/沙土相互作用关系进行了数值模拟, 从宏、细观角度研究了鸵鸟足趾底曲面的固沙限流机理和影响因素。
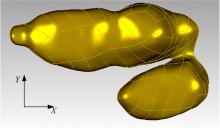
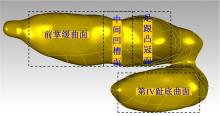
挑选一只具有成年非洲鸵鸟(以下简称鸵鸟)足部典型形貌特征的鸵鸟足作为研究对象, 如图1所示。鸵鸟足仅有两趾, 第Ⅲ 趾(内趾)较大, 末端具有较大的坚硬足趾甲, 第Ⅳ 趾(外趾)较小, 末端足趾甲退化为很小甚至消失, 并且鸵鸟足两趾底部均具有典型的曲面形貌。
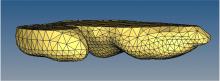
鸵鸟足底包括柱状乳突群和曲面结构, 剔除乳突群显露出鸵鸟足底曲面, 通过手持式非接触三维激光扫描仪对鸵鸟足底曲面进行扫描, 获取鸵鸟足底曲面三维数据点云图, 如图2所示。将三维点云数据导入逆向工程分析软件Geomagic Studio中进行处理, 经过噪声去除、点云删减、缺陷填补等修复工作, 得到鸵鸟足底曲面典型点云, 连接点云中的数据点得到三角形单元组成的几何体。经过轮廓线抽取及曲面片划分, 获得鸵鸟足底曲面重构模型。为了使鸵鸟足底触沙模拟界面接近鸵鸟站立姿态, 调整鸵鸟足在坐标系中的位置, 使鸵鸟足底基本与 
将Geomagic Studio中的文件导入Hypermesh中进行网格划分。在保证数值模拟准确性的前提下, 考虑到离散元数值模拟的计算时间, 针对不同功能区域进行不同尺度的网格划分。在网格划分时, 把整个足部分成上、下两部分, 在数值模拟时, 鸵鸟足下部分(足底及侧面)与颗粒直接接触, 是本研究的主体部分, 划分成细网格, 网格大小为1.5 mm; 鸵鸟足上部分(剖切平面及附近)仅用于施加约束和设定边界条件, 受力及形变精度对本研究结果影响较小, 划分成粗网格, 网格大小为6 mm, 如图4所示。本文研究鸵鸟足底曲面结构与沙土的相互作用, 尚未考虑材料特性的影响, 为便于将离散元软件EDEM与有限元软件Patran/Nastran结合来模拟分析, Hypermesh中鸵鸟足材料设置为钢, 密度为7.8 g/cm3, 泊松比为0.3, 弹性模量为1.82× 109 Pa, 并导出* .msh和* .bdf两个文件, 分别用于EDEM软件进行离散元模拟和Patran/nastran软件进行有限元静力学分析。
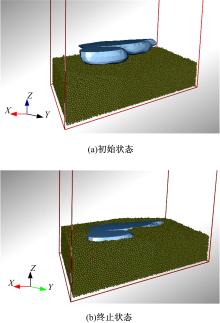
在EDEM离散元模拟中, 沙土密度为1.54 g/cm3, 泊松比为0.4, 弹性模量为4.7× 107 Pa[19], 鸵鸟足以2 mm/s的速度垂直下压, 当鸵鸟足整体沉陷在沙土颗粒中时, 模拟过程结束。图5为数值模拟起止状态, 初始到终止状态的计算时间为5.35 s。
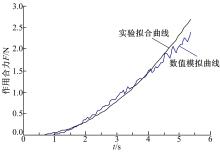
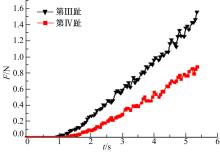
图6为实验和模拟中鸵鸟足底受到作用合力的动态变化图。从图6可以看出, 数值模拟结果与实验拟合曲线变化趋势基本一致, 表明鸵鸟足底/沙土相互模拟系统能够满足计算要求。
为了研究鸵鸟二趾足两趾底曲面形貌对沙土颗粒流动的影响, 文中分别选取鸵鸟足第Ⅲ 趾底曲面的前掌缓曲面、中间凹槽面和足跟凸冠面以及第Ⅳ 趾底曲面4个鸵鸟足底特征区域, 如图7所示。
在图7中, 各特征区域内的典型位置分别选取4个颗粒进行锁定跟踪, 通过分析区域内4个颗粒在模拟过程中的运动轨迹, 研究鸵鸟足底各特征曲面对沙土颗粒流动的影响规律。图8为鸵鸟足底特征区域内选定颗粒的模拟初始位置及模拟终止位置。由图8可以看出, 从鸵鸟足底接触沙土开始到鸵鸟足完全沉入沙土结束, 鸵鸟足底4个特征区域内选定颗粒位置发生变化, 总体上颗粒均向各自特征区域边缘运动。其中, 中间凹槽面的颗粒沿槽 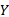
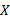
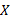

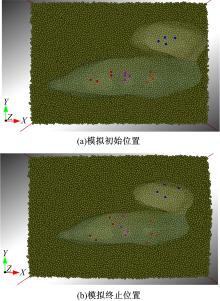 | 图8 鸵鸟足底特征区域内选定颗粒Fig.8 Final simulation position of the selected particles within each plantar characteristic zone of ostrich foot |
图9为鸵鸟足底特征区域内颗粒的模拟起止运动位移量。从图9可以看出, 在所有选定追踪颗粒中, 除了足跟凸冠面的94688号颗粒和中间凹槽面的6558号颗粒在 
 | 图9 鸵鸟足底特征区域内颗粒的模拟起止运动位移量Fig.9 Displacement amounts of the selected particles within each plantar characteristic zone of ostrich foot from the initial to the final simulation states |
将每个特征区域内选定的颗粒作为整体来看, 足跟凸冠面内颗粒在 
图10为鸵鸟二趾足两趾底曲面的动态受力图。从图10可以看出:从鸵鸟足底曲面接触沙土颗粒开始, 随着鸵鸟足下沉量增大, 与足底曲面接触的沙土颗粒逐渐增多, 鸵鸟足两趾底曲面受到的动态作用力均逐渐加大, 并呈近似于线性变化趋势。另外, 从鸵鸟足底接触沙土开始直到鸵鸟足完全沉没沙土结束, 鸵鸟二趾足第Ⅲ 趾底曲面受到的沙土动态作用力始终大于第Ⅳ 趾足底曲面, 并且受力差值越来越大。这一结果源于鸵鸟足第Ⅲ 趾和第Ⅳ 趾底曲面的面积和形貌影响。鸵鸟足第Ⅲ 趾底曲面面积是第Ⅳ 趾底曲面面积的两倍多, 将会导致第Ⅲ 趾底曲面受到的作用力相对较大。鸵鸟足第Ⅲ 趾底曲面由前掌平面、中部凹槽和后跟凸冠3个部分组成, 三者综合作用有助于固沙限流; 第Ⅳ 趾底曲面仅有凸冠, 沙土颗粒易于滑移, 因此也将造成第Ⅲ 趾底曲面比第Ⅳ 趾底曲面受到的作用力大。
鸵鸟足第Ⅲ 趾底曲面由三部分特征区域组成, 在鸵鸟足与沙土相互作用中发挥着决定性作用, 因此研究鸵鸟足第Ⅲ 趾底曲面下沙土颗粒的细观力学行为及趾底曲面典型特征区域建模具有重要意义。
图11为鸵鸟足第Ⅲ 趾底曲面作用下沙土颗粒动态接触力场。从图11(a)可以看出:当鸵鸟足第Ⅲ 趾底曲面与沙土颗粒刚接触时, 足跟凸冠面的冠顶部与颗粒接触, 产生应力集中现象, 颗粒受力迅速增大; 前掌缓曲面接近平面, 使沙土颗粒以较小力值与其完成初始均匀接触; 中间凹槽面此时尚未与沙土颗粒接触。从图11(b)可以看出:随着前掌缓曲面与沙土接触面积的增大, 平缓的前掌曲面使沙土颗粒主要产生向下的运动趋势, 而不易向周围方向运动, 从而增加了沙土颗粒的受力面积和接触力值; 足跟凸冠面的大曲率半径圆弧形貌使接触沙土颗粒易于沿凸冠表面向周围运动, 消弱了颗粒向下运动趋势, 从而颗粒受力范围和受力值较小; 此时前掌缓曲面下的沙土颗粒逐渐向中间凹槽面涌动并填充凹槽面区域, 并存在向足跟凸冠面移动的趋势。从图11(c)可以看出:颗粒受力密集区主要集中在前掌缓曲面、中间凹槽面及足跟凸冠面的前曲面, 并且颗粒受力面积和接触力值增大迅速, 这是由于涌向中间凹槽面的沙土颗粒受到足跟凸冠面前曲面的阻挡和前掌缓曲面下流动颗粒挤压的共同作用。从图11(d)可以看出:中间凹槽面的沙土颗粒群受力呈现网格状稳态分布, 并且沙土颗粒受力较大, 表明此区域已经形成“ 紧固” 状态。前掌缓曲面下的沙土颗粒受力较均匀并呈现后压趋势, 足跟凸冠面前曲面的阻挡加强了“ 紧固” 中间凹槽面沙土颗粒的作用。足跟凸冠面的大曲率半径圆弧难以稳定与其接触的颗粒, 使颗粒沿后斜下方运动趋势明显, 进一步解释了图8中足跟凸冠面下沙土颗粒位移变化的情况。
 | 图11 鸵鸟足第Ⅲ 趾底曲面作用下沙土颗粒动态接触力场Fig.11 Dynamic contact force fields of sand particles subjected to the third toe plantar surface of ostrich foot |
通过鸵鸟足第Ⅲ 趾底曲面下沙土颗粒的细观力学行为分析发现, 鸵鸟足第Ⅲ 趾底曲面的中间凹槽面具有明显的固沙限流作用, 因此本文利用激光扫描点云数据, 采用逆向工程技术和数学模型建立策略, 初步建立了鸵鸟足第Ⅲ 趾底中间凹槽面的数学模型, 为以后建立仿生数学模型及其应用奠定理论和技术基础。
首先, 基于鸵鸟足底曲面三维点云数据, 采用逆向工程技术处理软件, 分割并提取出鸵鸟足第Ⅲ 趾底中间凹槽面的三维点云数据; 其次, 通过三维点云数据过滤和修整, 获取适当数量并可显著表征鸵鸟足第Ⅲ 趾底中间凹槽面的三维典型点云数据; 最后, 采用MATLAB软件, 获取鸵鸟足第Ⅲ 趾底中间凹槽面的拟合曲面, 如图12所示。
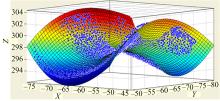 | 图12 鸵鸟足第Ⅲ 趾底中间凹槽面的拟合曲面Fig.12 The fitted curve surface of the middle groove in the third toe plantar surface of ostric |
鸵鸟二趾足第Ⅲ 趾底中间凹槽面的拟合曲面方程为:
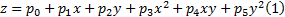
式中: 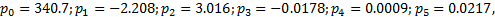
该拟合曲面方程的残差平方和为441.6, 标准误差为0.4604(小于1), 确定系数为0.9607(接近1), 表明该曲面方程具有较高的拟合精确度。
为了研究沙土颗粒对鸵鸟足趾底曲面形变的影响, 将Hypermesh软件划分网格后导出的* .bdf文件以及EDEM软件中数值模拟终止时刻鸵鸟足每个网格单元的三维作用力导入Patran/nastran软件中, 设置边界条件及相关参数, 进行有限元数值计算。
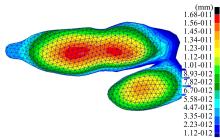
图13为有限元数值计算以后鸵鸟足底曲面变形图。从图13可以看出, 鸵鸟足底曲面变形位置集中在第Ⅲ 趾底曲面的前掌缓曲面后半段、足跟凸冠面前半段以及两段之间的中间凹槽面, 其中最大变形值位于中间凹槽面的两侧壁位置。第Ⅳ 趾底曲面变形明显小于第Ⅲ 趾底曲面。鸵鸟二趾足底曲面形变规律表明, 鸵鸟足第Ⅲ 趾底多曲面结合形貌在鸵鸟足越沙过程中发挥着至关重要的作用, 同时进一步验证了鸵鸟足第Ⅲ 趾底中间凹槽面的固沙限流作用。
(1)采用逆向工程技术, 进行了鸵鸟足底曲面三维重构。将鸵鸟足底曲面分为鸵鸟足第Ⅲ 趾底曲面的前掌缓曲面、中间凹槽面和足跟凸冠面以及第Ⅳ 趾底曲面四个鸵鸟足底特征区域, 并进行了鸵鸟足底曲面/沙土相互作用离散元模拟。
(2)鸵鸟足底曲面下沙土颗粒流动程度沿足宽方向大于沿足长方向, 表明鸵鸟足底曲面形貌减缓鸵鸟足前行滑移程度明显优于侧向滑移。鸵鸟足第Ⅲ 趾底曲面比第Ⅳ 趾底曲面受到更大的沙土颗粒作用力, 这一结果源于鸵鸟足第Ⅲ 趾和第Ⅳ 趾底曲面的面积和形貌差异。
(3)在鸵鸟足第Ⅲ 趾底曲面特征区域的固沙限流效果方面, 中间凹槽面最好, 此区域的沙土颗粒群受力呈现网格状稳态紧固分布, 前掌缓曲面次之, 此区域的平缓曲面易于下压沙土颗粒, 减缓了周向运动; 足跟凸冠面最差, 此区域的大曲率半径圆弧形貌使接触沙土颗粒易于沿凸冠表面向周围运动, 使沙土颗粒处于不稳定状态。
(4)基于鸵鸟足底曲面三维点云数据, 进行了鸵鸟足第Ⅲ 趾底中间凹槽面的曲面拟合及方程获取, 该曲面方程具有较高的拟合精确度, 为鸵鸟足底曲面仿生设计提供了重要理论依据。
(5)鸵鸟二趾足底曲面形变有限元分析表明:鸵鸟足第Ⅲ 趾底多曲面结合形貌在鸵鸟足越沙过程中发挥着至关重要的作用, 并进一步验证了鸵鸟足第Ⅲ 趾底中间凹槽面的固沙限流作用。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|