董冰(1982-),男,博士研究生.研究方向:复杂系统建模,优化与控制,电动汽车.E-mail:dongbing_jlu@126.com
以纯电动汽车能量管理系统为研究对象,通过分析动力电池系统与高压系统部件结构,确定了能量管理系统功率流关系。针对常用的能量管理系统控制策略,依据整车及电池特性,引入了能量管理系统功率分配系数,设计了以模糊控制器为核心的优化控制方法,并进行了仿真分析与验证。最后,通过转鼓台架的控制策略对比实验,验证了该优化方法可以有效地降低整车能量消耗率,且在动力电池总能量不变的前提下,使整车拥有较理想的经济性能和动力性能。
This paper studies the energy management of pure electric vehicles. By analyzing the structure of the power battery system and the components and parts of high voltage system, the power flow relationship of the energy management system is confirmed. Aiming at the controlling strategy of common energy management system, the power distribution coefficient of the system is introduced based on the characteristics of the vehicle and battery. An optimal control method based on fuzzy controller is designed, analyzed and validated by simulation. Finally, comparison experiments of the control strategy are carried out on a drum test bench. Results show that this optimal control method can reduce the energy consumption ratio effectively, and under the condition that the total energy of the battery is steady, the vehicle can keep ideal economic performance and ideal dynamic property.
纯电动汽车能量管理系统的功用就是在满足整车基本动力性、驾驶平稳性等技术性能和成本等要求的前提下, 根据各高压系统部件的特性及汽车的运行工况, 实现能量在能源转换装置之间按最佳路线流动, 使整车的能源利用效率达到最高。
目前国内外能量管理系统控制方法主要有两种:一是降低整车能量使用率法, 它通常不使用热管理系统[6, 7], 只保留车辆行驶必需的高压负载, 以此来最大程度地降低整车高压系统功耗, 把有限的功率全部分配到驱动系统; 二是提高电池使用效率法, 它通过热管理系统的使用, 把电池控制在高效能区间[8, 9]。对于方法一, 虽然可以最大程度上节约电能, 但电池的加速老化会牺牲整车的经济性。对于方法二, 最常用的是门限值控制法, 虽然控制策略简单稳定, 但由于控制规则固定, 不能最优地解决功率分配问题, 影响整车动力性。
本文通过分析动力电池系统与高压系统部件结构, 确定了能量管理系统功率流关系, 在深入分析现有能量管理系统控制方法的基础上, 对能量管理系统控制方法进行了数学抽象, 引入了能量管理系统功率分配系数, 使上述两种方法在数学模型上达到统一。同时, 提出了能量管理系统优化控制目标, 并确立了可实现优化目的模糊控制方法。通过合理设计模糊控制器, 完成了对能量管理系统控制结果的优化。通过转鼓台架上的控制策略对比实验, 证明了该方法有较理想的经济性和动力性。
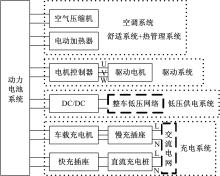
纯电动汽车高压系统部件主要分为:空调系统部件, 驱动系统部件, 低压供电系统部件和充电系统部件, 如图1所示。其中, 低压供电系统部件通过DC/DC将高压电转化为低压电, 用以支持全车电子零部件、助力转向、水泵和风机等低压设备的运转; 充电系统部件通过充电机或其他充电设备从电网补充能量; 空调系统部件主要用于提升驾驶员舒适度和动力电池的热管理, 空调系统部件中消耗功率的高压部件为加热使用的电动加热器和制冷使用的空气压缩机; 驱动系统部件用于驱动电机对外做功, 也可以制动回收部分能量。
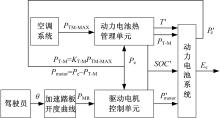
由上述动力电池系统和高压系统部件结构, 可得到如图2所示的整车能量管理系统功率流示意图。它描述了动力电池系统及整车高压系统之间功率流的输入输出关系。图中, Pbat为动力电池系统的最大输出功率; 能量管理系统分配到空调系统的最大功率为PA-C, 由于舒适系统和热管理系统共用功率器件, 为直观描述其功能, 将空调系统等效为热管理系统, 称之为PT-M; Pmotor为能量管理系统可分配给驱动系统的最大功率; PL-P为低压供电系统的需求功率; Pcha为充电系统最大可充电功率。
在车辆行驶过程中, Pcha(t)为0, PL-P(t)为定值, 数值上等于DC/DC额定功率, 是必须分配的量。PT-M(t)和Pmotor(t)的大小则根据不同工况下功率总线需求功率来确定, 是可调节分配的量。令整车能量管理系统可分配的功率为Pe(t), 则:
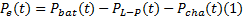
显然, 整车能量管理系统的目的是合理地将Pe(t)分配给PT-M(t)和Pmotor(t), 使得整车的能源利用效率达到最高。
能量管理系统控制策略通常采用门限值控制方法, 即:设置一个关于剩余能量的 
现引入一个能量管理系统功率分配系数KT-M(t), 它表示Pe(t)分配给热管理系统的最大功率的权值, 定义域为[0 1], 则分配到热管理系统的最大功率为:

式中:PTM-MAX(t)为热管理系统高压部件的峰值功率。
分配给驱动系统的最大功率为:
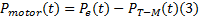
将式(2)代入式(3)得:

当KT-M(t)恒为0时, 即为降低能量使用率方式, 最大程度上把有限的电池功率分配到驱动系统。
在能量管理系统门限值控制方法中, KT-M(t)为变化量, 控制策略如下:对于Pmotor(t)=Pe(t)-KT-M(t)PTM-MAX(t), 当KT-M(t)=0时, SOC(t)≤ SOCTH; 当KT-M(t)=1时, SOC(t)> SOCTH。其中, SOCTH为门限阈值。
能量管理系统门限值控制流程如图3所示。驾驶员踩踏加速踏板, 通过加速踏板开度(θ )曲线, 了解驾驶员驾驶意图[10], 获得电机需求功率PMR; 能量管理系统可分配功率Pe, 依据门限值控制策略, 将功率分配到热管理系统和驱动系统。当系统完成做功后, 动力电池能量变成了E'e, 最大可分配功率变成P'e, 同时动力电池的温度变成T'和荷电状态变成SOC'。
能量管理系统的优化目的是在动力电池能量一定的条件下, 通过合理分配驱动系统和热管理系统承担的功率(即调节两者的功率分配因子), 使得车辆的能量消耗率 
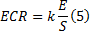
式中: 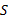


本文在常规能量管理系统控制策略上增加了一个优化单元, 通过在[0, 1]区间动态调整 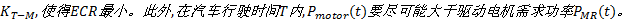
由上述分析可建立如下的纯电动汽车能量管理系统优化问题的数学模型:
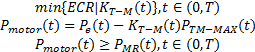
可以看出, 此问题属于典型的带约束非线性优化问题。
影响纯电动汽车能量管理系统功率分配的主要参数有:t时刻加速踏板开度变化率dθ /dt; t时刻电池温度与电池最佳温度工作区间的温度差Δ T。当Topti-min≤ Tbat≤ Topti-max时, Δ T=0; 当Tbat≥ Topti-max或Tbat< Topti-min时, Δ T=min{|Topti-min-Tbat|, |Topti-max-Tbat|}。其中, Topti-max为电池最优工作温度区间上限值; Topti-min为电池最优工作温度区间下限值; Tbat为电池温度, 由于动力电池本体温度的不一致性, 在实际计算中取其平均值。
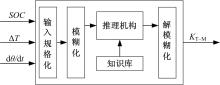
依据上述分析, 建立如图4所示的优化控制流程, 它在原控制策略基础上增加了能量管理系统功率分配模糊控制器, 以SOC(t)、dθ /dt和Δ T为参数输入, 输出控制参数KT-M, 热管理系统和驱动系统按KT-M 的功率分配系数做功后, SOC(t)和Δ T发生改变, 再反馈给模糊控制器作为下一次的输入, 形成闭环。
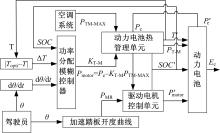 | 图4 基于模糊逻辑的能量管理系统优化控制流程图Fig.4 Procedure of the energy management system based on fuzzy logic optimal control |
纯电动汽车能量管理系统模糊控制器采用三输入、单输出的mamdani结构, 如图5所示。三输入分别为:电池荷电状态SOC, 温度差Δ T和加速踏板开度变化率dθ /dt, 输出为能量管理系统功率分配系数K_T-M(t)对控制器的输入输出进行归一化, 使得所有输入与输出的论域都为[0, 1]。对于SOC, 0表示动力电池剩余电量较低; 1表示动力电池剩余电量较高。对于Δ T, 0表示当前电池温度与最优电池温度的温差较小; 1表示当前电池温度与最优电池温度的温差较大。对于dθ /dt, 0表示驾驶员踩加速踏板的频率较低, 即车辆正常行驶; 1表示驾驶员踩加速踏板的频率较高, 即车辆急加速或爬坡行驶。对于KT-M (t), 0表示需要热管理的程度较低; 1表示需要热管理的程度较高。
由于受设计者主观因素的影响, 隶属度函数的确定往往呈现出多样性, 常见确定隶属度函数的方法有模糊统计方法、指派方法、专家法、二元对比排序法和借用已有的“ 客观” 尺度法[12]。经查阅与本领域相近的参考文献, 采用高斯型隶属度函数的相对较多, 因此借用已有的“ 客观” 尺度, 所设计的模糊控制器输出变量和输入变量的隶属度函数均采用高斯型, 且输入变量的高斯点相同, 如图6所示。
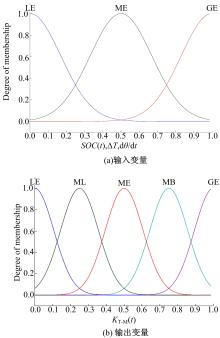 | 图6 模糊控制器的输入变量和输出变量的隶属度函数图Fig.6 Membership function between output and input variable in fuzzy controller |
输出和输入变量的模糊子集分别定义如下:
KT-M(t):{LE, ML, ME, MB, GE};
SOC(t):{LE, ME, GE};
Δ T:{LE, ME, GE};
dθ /dt:{LE, ME, GE};
其中, LE为较小(Little); ME为中(Mediurn); GE为较大(Greater); M为中小(MediumLittle); MB为中大(MediumBig)。
纯电动汽车能量管理系统工作过程描述如下:
(1)当车辆起步时, 如果动力电池工作温度Tbat较低, 优先满足PT-M。
(2)当车辆起步时, 如果动力电池工作温度Tbat正常, 优先满足Pmotor。
(3)当汽车急加速或爬坡行驶时, 即dθ /dt大于某设定的阈值, 优先启动Pmotor, 满足驱动电机高功率需求, 再启动PT-M。
(4)当汽车以正常速度行驶时, 即dθ /dt小于某设定的阈值, 优先满足PT-M, 提高充放电效率, 再满足Pmotor, 保证驱动电机普通功率需求。
(5)如果电池 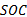
(6)如果电池 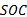
依据上述工作过程, 在制定模糊控制规则时, 遵循如下基本原则:
(1)电池剩余电量 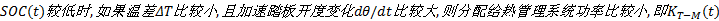
(2)电池剩余电量 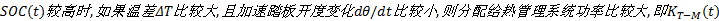
能量管理系统优化模糊控制策略采用IF-THEN规则, 共建立了27条规则库。规则如表1所示, 模糊推理曲面如图7所示。
| 表1 模糊控制规则表 Table 1 Rule of the fuzzy control |
选取车辆常见的坡路、平路、空载和满载4种工况, 对模糊控制器进行模拟工况的仿真验证, 结果如图8所示。
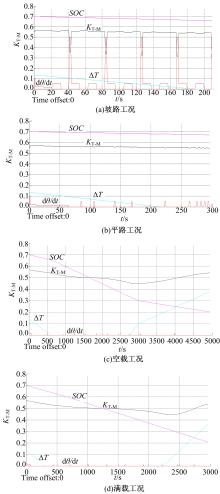 | 图8 模糊控制器的不同模拟工况仿真验证Fig.8 Simulation and verification under the differentdriving cycle by fuzzy controller |
对于坡路工况, dθ /dt比较大, 因此KT-M 会随着dθ /dt的陡然升高而迅速降低; 而平路工况, dθ /dt变化并不明显, KT-M只会沿着SOC的趋势慢慢走低, 由于坡路和平路的循环时间不长, SOC和温度的变化并不明显。对于满载工况, 在300 s附近电池升温到最优工作温度区间, KT-M降低, 当运行到2300 s附近时, 电池温度超过最优工作温度区间, KT-M升高; 而空载工况, 在600~2700 s内电池处于最优工作温度区间, KT-M相对较低, 在超出这个范围之后, 即使 
基于模糊逻辑的能量管理系统优化控制方法的求解过程如图9所示。其中, EBAT为电池额定能量, 数值上等于标称电压乘以标称容量; Topti为最优工作温度区间的上下限值, 可以通过实验获得; 
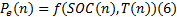
函数对应关系如图10所示。
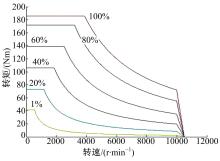
由加速踏板开度 θ 及电机当前转速N可离线标定获得电机需求转矩T, 如图11所示。而电机需求功率满足:
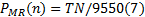
P'motor (n)为电机实际输出功率。当Pmotor(n)≥ PMR (n)时, 表示当前能量管理系统功率可以满足整车动力性要求, 令:P'motor (n)=P_MR (n); 当Pmotor (n)< P_MR (n)时, 表示当前能量管理系统功率不能满足整车动力性要求, 为欠功率状态, 令:P'motor (n)=Pmotor (n)。显然, 欠功率状态时间越短, 整车动力性越好。
Ee (n+1)为当前整车完成做功后剩余的动力电池能量, 在记录下行驶里程后, 可依据式(5)计算得到ECR。
 | 图9 基于模糊逻辑的能量管理系统优化控制方法求解过程Fig.9 Solution procedure of the energy management system optimal control method based on fuzzy logic |
为了评价模糊控制方法的有效性, 利用AVL Cruise仿真软件, 对比门限值控制法进行仿真验证实验, 车辆仿真参数如下:整备质量为1510 kg; 满载质量为1960 kg; 迎风面积为2.15 m2; 风阻系数为0.315; 摩擦因数为0.015; 电池额定能量为23 kWh; 电机额定功率为42 kW; DC/DC额定功率为1.8 kW; 空调压缩机峰值功率为6 kW; 电动加热器峰值功率为5.2 kW。
图12是NEDC、EUDC、UDC和US06四种不同工况下的 SOC变化图。从图中清晰可见:电池SOC在行车过程中不断下降, 且在使用模糊控制方法时, 比使用门限值控制方法下降得要缓慢。这说明在相同条件下, 模糊控制方法的电池使用效率比门限值控制法要高。4种工况下不同控制策略的ECR仿真结果如表2所示。由表2清晰可见:模糊控制的ECR比门限值法有大幅度的提高。
| 表2 不同工况的ECR仿真结果 Table 2 ECR simulation result of the different driving cycle |
实验1 电池最优工作温度区间的获取。
实验设备为电池整包充放电柜, 上限电压为600 V, 上限电流为500 A, 峰值功率为150 kW。温度仓容积为3 m× 2 m× 1 m, 温度范围为-60~120 ℃。
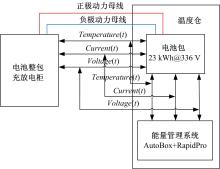
实验目的:测得电池最优工作温度区间, 作为优化控制方法的重要输入参数。实验用电池系统测试台架结构如图13所示。
电池整包充放电柜为温度仓中的电池包输入高压电源, 同时与电池包及能量管理系统进行温度、电流和电压的数据交互与存储。能量管理系统通过快速原型(RCP)实现。
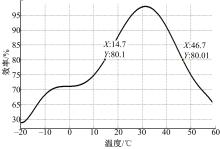
整车行驶过程中提高电池使用效率, 实际是提升电池放电效率。电池放电效率是指电池在一定放电制度下放电至电池放电截止电压所放出来的实际电量与额定电量之比[14]。电池在不同环境温度下, 100%DOD放电可以测得不同环境温度下的电池放电效率。图14为多组放电实验后拟合获得的电池放电效率曲线。
从图14可以看出, 在环境温度高于46.7 ℃或者低于14.7 ℃时, 实验用锂离子动力电池的放电效率下降很快。因为在低温下电解液的浓度变大, 锂离子从负极材料脱嵌出来的速度变慢, 同时由于电池的内阻增大, 导致放电平台迅速下降, 提前达到放电截止电压, 所以其放电容量下降, 放电效率降低; 在温度处于常温区时, 电池内部材料的活性增强, 锂离子扩散速度增加, 其放电容量上升, 放电效率升高; 但是在过高的温度下, 电池电极材料的物理特性将发生不可逆的衰减, 反应强度减弱, 所以其放电容量下降, 放电效率降低。在温度高于46.7 ℃或者温度低于14.7 ℃时, 电池的放电效率均低于80%。
通过实验可以得到以下结论:在固定倍率(1/3C)放电时, 实验用锂离子电池在14.7~46.7 ℃温度范围之内, 放电效率可以达到80%以上, 即14.7~46.7 ℃为最优工作温度区间。由于放电倍率越大, 电池呈现的放电能力越低, 所以小倍率(1/3C)的最优工作温度区间一定包含大倍率的最优工作温度区间。由于电动汽车工况的复杂性, 研究选择更宽泛的小倍率最优工作温度区间作为实验用的最优工作温度区间。
实验2 控制策略的转鼓实验台架验证。
实验设备为转鼓实验台, 最大吸收/驱动功率≥ 145 kW, 最大吸收/驱动扭矩≥ 6000 Nm, 最高测试车速≥ 200 km/h。转鼓实验设备如图15所示。
 | 图15 相同条件下的不同控制策略转鼓台架实验Fig.15 Experiment of the drum test bench with different control method under the same driving cycle |
实验目的:在转鼓控制台上输入实验工况, 设定驱动系统需求功率。通过修改RCP的能量管理系统控制策略, 在整车上进行相同工况下不同控制策略的结果对比验证。实验分为3组, 第1组测无热管理控制法, 第2组测门限值控制法, 第3组测模糊控制法。其中每组实验重复3次, 最终取剩余 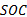
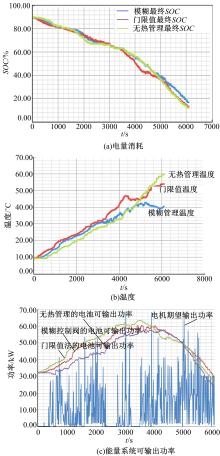 | 图16 相同条件不同控制方法下的电量消耗、温度及能量系统可输出功率Fig.16 Energy consumption, temperature and energy system power output of the different control method under the same driving cycle |
由图16(a)可见, 在工况初期, 无热管理方式的 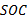
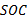
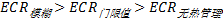
图16(c)是相同条件下不同控制方法的能量系统可输出功率对比图, 蓝色为驱动电机需求功率, 紫色为无热管理法, 绿色为门限值法, 红色为模糊法。由图可知, 门限值法在初期优势比较明显, 模糊法居中, 无热管理法稍差。这是因为带热管理系统的控制方式电池使用效率较高; 中后期时模糊法优势比较显著, 因为模糊控制方式电池使用效率较高, 且能量消耗率较低, 可调节的KT-M系数可以有效地兼顾温度和能量消耗率, 使得欠功率的时间少于其他两种方法。因此整个工况结束后, 采用模糊法的纯电动汽车动力性优于门限值和无热管理两种控制方式。
通过确定纯电动汽车能量管理系统的功率流关系, 在充分了解当前控制策略的基础上, 引入了能量管理系统功率分配系数, 提出能量管理系统优化控制目标, 制定了基于模糊逻辑的纯电动汽车能量管理系统优化方法。对优化方法中核心的模糊控制器进行了不同工况下的仿真分析, 表明模糊控制器符合设计规则要求。实验结果表明:优化控制方法的ECR低于门限值控制法和无热管理控制法, 相比两者有较好的经济性。而在低 
本文的研究主要基于某车厂示范运营项目的城市实际工况和一些常用的工况循环, 并没有涵盖太多的特殊情况。因此, 下一步的研究方向可以根据不同循环工况的特点, 通过调整模糊控制模型输入输出隶属度函数的方法, 改善所制定控制策略的工况适应性, 并制定基于循环工况和动态规划的全局优化控制策略, 目的是解决能量管理系统分阶段决策过程中前一阶段的控制效果会严重影响下一阶段控制效果的优化控制问题, 使所制定的控制算法能够保证整个循环的全局最优。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|