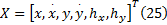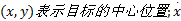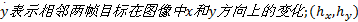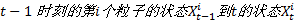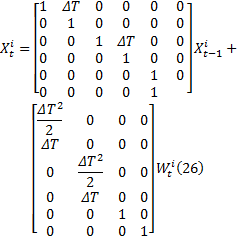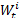引用本文
杨欣, 刘加, 周鹏宇, 周大可. 基于多特征融合的粒子滤波自适应目标跟踪算法. 45(2): 533-539
YANG Xin, LIU Jia, ZHOU Peng-yu, ZHOU Da-ke. Adaptive particle filter for object tracking based on fusing multiple features. Journal of Jilin University Engineering and Technology Edition, 45(2): 533-539  
Permissions
Copyright©2015, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于多特征融合的粒子滤波自适应目标跟踪算法
杨欣1,2,3, 刘加1, 周鹏宇1, 周大可1
1. 南京航空航天大学 自动化学院,南京 210016
2.东南大学 自动化学院,南京 210096
3.光电控制技术重点实验室,河南 洛阳 471000
刘加(1989-),男,硕士研究生.研究方向:模式识别与图像处理.E-mail:lergliu@126.com

杨欣(1978-),男, 副教授, 博士.研究方向:模式识别与智能系统.E-mail:yangxin@nuaa.edu.cn

基金:国家自然科学基金项目(61172135, 61101198).航空科学基金项目(40145152027)
摘要

为解决用单一特征无法保持在复杂环境下跟踪的鲁棒性以及粒子数量增多导致的算法效率低下的问题,选择多个特征融合的策略来保证跟踪的持续稳定,并自适应地调整每个特征的权值来适应环境的变化;为提高算法的实时性,采用自适应的粒子数量。实验结果表明:本文算法有效地解决了目标旋转、目标遮挡以及背景混淆等诸多问题,具有较高的鲁棒性。

关键词: 自动控制技术; 目标跟踪; 粒子滤波; 多特征融合; 自适应
中图分类号:TP29 文献标志码:A 文章编号:1671-5497(2015)02-0533-07
Adaptive particle filter for object tracking based on fusing multiple features
YANG Xin1,2,3, LIU Jia1, ZHOU Peng-yu1, ZHOU Da-ke1
1.College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016,China
2.School of Automation, Southeast University, Nanjing 210096,China
3.Key Laboratory of Photoelectric Control Technology,Luogyang 471000,China
Abstract

In target tracking using a single feature, the tracking robustness can not be guaranteed in the case of complex environments, and the increase in particle number will lead to in low efficiency of the algorithm. To overcome these problems, a multiple feature fusion strategy is chosen to ensure sustained and stable tracking. Using this strategy, the weights of features will be adjusted adaptively to the environmental changes, and the number of particles is adaptive to improve the efficiency of the algorithm. Experimental results show that the proposed algorithm can effectively solve the target rotation, target occlusion, background confusion and many other issues with high robustness.

Keyword: automatic control technology; objects tracking; particle filter; multi-feature fusion; adaptive
引言

视频目标跟踪是人工智能研究领域的热点之一, 在很多场合下都有非常重要的应用, 如视频监控、人机交互等。目标跟踪的本质是通过对视频序列进行统计分析, 获得观测数据, 以对目标的状态进行估计与预测。其中, 目标的状态包括目标在每帧图像中的位置、大小、运动速度、加速度等。对目标状态进行估计与预测的问题可转化为在贝叶斯(Bayesian)理论框架下已知目标状态的先验概率及新的观测值来求取状态的最大后验概率的过程。对于线性、高斯系统下的跟踪问题, 可以用卡尔曼滤波(Kalman Filter)来解决, 然而实际的跟踪问题往往是非线性、非高斯的, 这类情况下可以用扩展卡尔曼滤波(Extended Kalman filter, EKF), 此方法需对模型线性化, 并要求期望的概率密度函数满足高斯分布。为此, 一种称之为序贯蒙特卡洛(Sequential monte carlo, SMC)的方法被提出用于解决这类非线性非高斯系统问题。序贯蒙特卡洛的方法也称为粒子滤波(Partical filter)。

基于粒子滤波的目标跟踪可以认为是序列图像帧间目标相关特征的对应匹配。对粒子滤波算法而言, 有一个重要的缺陷是粒子数匮乏。文献[1]提出遗传粒子滤波器, 使重采样阶段粒子退化问题得到了解决。文献[2]采用CamShift优化的粒子滤波跟踪方法, 有效地解决了粒子的退化问题。但该文献只使用了颜色特征来进行跟踪, 易受背景中颜色相似物体的干扰, 且颜色特征对光照较为敏感。文献[3]提出了基于颜色特征和纹理特征相结合的方法来提高目标跟踪的鲁棒性, 但特征权值固定, 跟踪精度得不到保证。跟踪稳定性和鲁棒性是衡量目标跟踪问题的重要性能指标。为了保证跟踪精度, 在跟踪过程中, 随着粒子数的增加, 会出现计算复杂度增大的问题, 使粒子滤波的性能恶化。文献[4]引入估计窗概念, 用来降低算法的计算复杂度。文献[5-6]对算法重采样阶段的计算复杂性进行了详细分析, 并给出了硬件的设计方法。为解决用单一特征无法保持在复杂环境情况下跟踪的鲁棒性以及粒子数量增多导致的算法效率低下的问题。本文选择多个特征融合的策略来保证跟踪的持续稳定, 为提高算法的实时性, 采用自适应的粒子数量。

1 基本粒子滤波算法

所谓粒子滤波, 是指通过寻找一组在状态空间中传播的粒子, 对概率密度函数进行近似, 以样本均值代替积分运算, 从而获得状态的最小方差估计的过程。它的实质是构造状态变量的后验概率密度, 经过状态更新和时间更新, 当粒子数目足够多时, 粒子的概率密度函数就逐渐逼近状态的概率密度函数, 粒子滤波的估计就逼近最优贝叶斯估计。

系统的模型可表示为[7]:

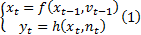
式中: xt 和yt分别为系统在t时刻的状态值和观测值; vt 和nt分别为过程噪声和观测噪声。

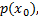
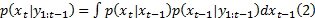
假设状态的先验分布为 则状态预测方程为:

状态更新方程为:

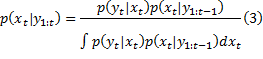
式(3)中存在积分运算, 对非线性非高斯系统, 得不到解析解。蒙特卡罗方法可将积分运算变为有限样本点的求和运算。从状态从状态从状态x0:t 的概率分布密度函数p(x0:t |y1:t)中抽取N个样本{xi0:t, i=1, 2, …, N}, 状态概率密度分布可近似表示为:状态概率密度分布可近似表示为:状态概率密度分布可近似表示为:

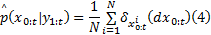
式中:δ (· )为狄拉克函数。

根据序列重要性采样原理, 当样本数量足够多时, 状态的概率密度函数可表示为:

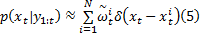
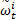
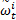
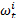
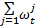
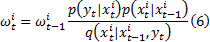
式中: 为归一化粒子重要性权值, = / , 其中 为:

式中: 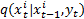为重要性密度函数, 粒子由采样得来。

2 多特征融合的观测模型
2.1 颜色特征

颜色特征是目标最主要的特征之一, 对目标的旋转及姿态变化具有一定的鲁棒性和持续性, 经常用于目标跟踪。为消除RGB颜色空间中R、G、B通道的相关性, 本文在HSV空间内对目标进行建模, 将特征空间平均划分为m个等级。假设目标区域内总像素个数为N, 中心为x0=(x, y), 半径为h=(hx, hy), 目标区域内单个像素为xi, 则目标区域内的颜色直方图可表示为[8]:

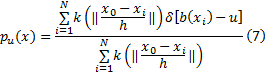
式中:函数函数b(xi)为xi处的像素对应直方图的索引值; u=1, 2, …, m表示直方图中颜色的等级索引; ‖ x0-xi‖ 表示xi 到x0 的距离; k(· )为一权值函数, 其主要是使离目标中心近的像素被赋予较大的权值, 定义如下:为一权值函数, 其主要是使离目标中心近的像素被赋予较大的权值, 定义如下:

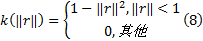
在得到颜色分布后, 采用Bhattacharyya距离来描述目标模板和候选目标的相似性, 假设目标模板的颜色分布为p(x)={pu (x)} u=1, …, m, 候选目标的颜色分布为q={qu }u=1, …, m, 则p(x)和q的Bhattacharyya系数为[9]:

的相似程度可表示为:

的值越小, 说明两者的相似度越大, 则候选目标为真实目标的可能性就越大。

2.2 边缘特征

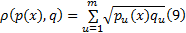
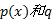
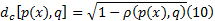
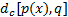
基于颜色特征的跟踪能够适应大多数的背景, 但当目标和背景存在着相似的颜色特征时, 单一特征的跟踪往往会把背景误当作目标。而边缘直方图描述了目标的结构信息, 包括目标的形状和边缘信息, 使用边缘特征能够很好地适应背景的颜色变化。

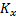
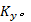
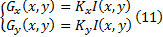
边缘信息是在灰度图像中获取的, 所以先把彩色图像转换为灰度图像。边缘检测采用水平Sobel算子 和垂直Sobel算子

式中: 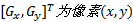处的梯度向量。

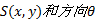
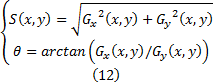
边缘的大小 分别为:

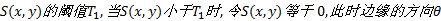
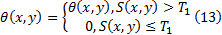
为消除噪声的影响, 设置了 也为0, 即:

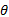
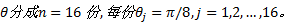
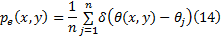
边缘方向 的取值范围是0~2π , 将 统计各个角度区间内边缘的大小并归一化, 得到目标的边缘直方图:

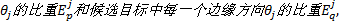
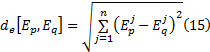
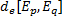
统计出目标模板中每一个边缘方向 两者的相似度可用如下公式来度量:

的值越小, 说明两者的相似度越大, 则候选目标为真实目标的可能性就越大。

2.3 纹理特征

纹理特征是一种很重要的描述图像信息的特征, 它反映了图像本身的属性, 具有很强的抗光照突变性。灰度共生矩阵是图像纹理分析方法中的一种, 它通过研究灰度的空间相关特性来描述纹理, 是纹理分析领域中最经常采用的特征之一。基于灰度共生矩阵的纹理特征具有抗噪声和遮挡的能力, 且提取简单, 处理速度快, 很好地满足了目标跟踪的实时性和精度要求。

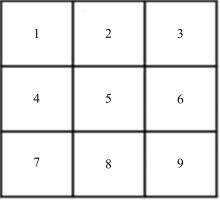
灰度共生矩阵表示了灰度的空间依赖性, 它表示了在一种纹理模式下的像素灰度的空间关系。灰度共生矩阵是对图像上保持某距离的两像素分别具有某灰度的状况进行统计得到的。基于灰度共生矩阵纹理特征的描述如图1所示。

图1 像素分布图Fig.1 Pixel distribution

假设位于位置5上的像素灰度值为Gx, y, 其中横向为x方向, 纵向为y方向。针对选中跟踪目标区域(假设为M× N像素大小)的灰度图像, 分别计算每个像素与45° 、135° 、90° 和0° 方向上像素的灰度之差, 即:

根据式(16)得到G1 、G2 、G3 和G4 共4个灰度差值共生矩阵。此时提取的灰度共生矩阵并不能直接作为纹理特征, 需进行二次统计量的计算, 这里采用和均值G5矩阵:

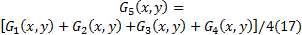
类似颜色直方图, 可得到图像的基于纹理特征的灰度直方图, 进而可得到目标模板与候选目标的纹理相似度dt[Ep, Eq]。

2.4 融合策略

对于多特征的粒子滤波跟踪算法, 会有多个观测似然函数, 单个特征的观测似然函数可设计为:

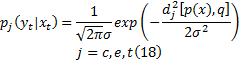
式中: 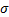为高斯方差。

式(18)的值越大, 说明候选目标与目标模板的特征分布越接近, 则候选目标为真实目标的可能性就越大。

多特征融合得到的基于多个观测值的融合概率密度函数会具有多个单特征的优点, 跟踪效果更好。假设颜色、边缘和纹理这三个观测过程是独立的, 则基于多个观测值的融合概率密度函数可定义为:

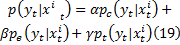
式中: 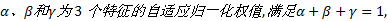3个权值会在跟踪过程中根据特征的相似度自适应地调整, 相似性越大的特征, 赋予的权值也应越大。

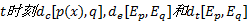
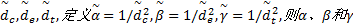
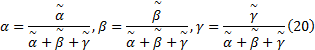
分别取 的平均值 可表示为:

为减小当环境突变导致某一特征突然变化带来的跟踪偏差, 可设定一阈值消除这种影响, 即特征的相似度达到阈值时特征才能响应, 设定响应阈值T2, 响应规则如下:

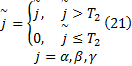
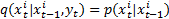
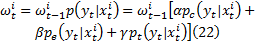
本文选择 为重要性密度函数, 则由式(6)推导得到粒子的权值的递推公式为:

2.5 粒子数自适应调整策略

当背景较简单、目标状态估计的误差较小时, 采用较少数量的粒子即可达到稳定的跟踪; 当目标所处的背景较复杂、目标本身变化较大或者目标被遮挡时, 则需要增加粒子的数量来搜索目标的可能位置。本文对粒子数的选取所采取的自适应策略是:若当前时刻目标预测比较准确, 则在下一时刻可适当减少粒子数; 反之, 若发生目标被遮挡或者背景突变等导致跟踪误差较大, 则应适当增加粒子数。定义当前目标预测状态与真实目标状态的相似度为:

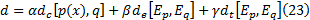
粒子数可按如下策略自行调整:

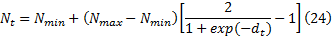
式中:Nmax和Nmin分别为设定的粒子数量的最大值和最小值。

3 算法实现
3.1 运动模型

目标的状态可表示如下:

式中: 和 表示目标的大小。

可描述如下[10]:

式中:Δ T为采样周期; 为高斯白噪声。

3.2 算法步骤

本文采取的基于多特征融合的自适应粒子滤波跟踪算法的实现步骤如下:

步骤1 初始化。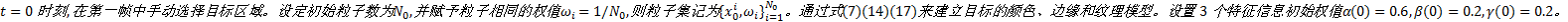

步骤2 重要性采样。根据式(26)进行采样, 得到新粒子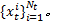

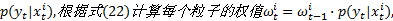
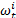
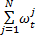
步骤3 权值更新。根据式(19)计算每个粒子状态对应的融合观测似然函数值 归一化权值, ti= / 。

步骤4 重采样:

(1)计算有效粒子数Neff=1/ 。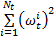

(2)若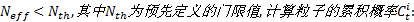

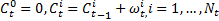
(3)在[0 1]区间生成一组均匀分布的随机数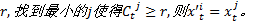

步骤5 状态预测, = 。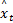

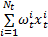
步骤6 多特征权值的更新。根据式(20)来调整在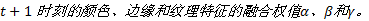

步骤7 粒子数量更新。根据式(24)计算在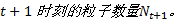

步骤8 置 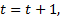返回步骤2。

4 实验结果与分析

为验证本文算法的检测结果, 在AMD A6-3420M, 1.50 GHz的PC机上用Matlab进行了仿真实验。实验中选取高斯函数作为核函数, 高斯方差 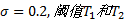分别被设为90和0.15。

图2 飞机模型跟踪实验Fig.2 Model aircraft tracking experiment

实验1 选取在空中飞行的飞机模型作为跟踪目标, 此时背景不复杂, 粒子数选择为较小的值50。图2(a)是使用单一颜色特征跟踪的结果。可以看出:跟踪初期, 矩形框的中心一直在目标中心摆动, 随着时间的累积, 矩形框开始漂移, 到30帧时, 矩形框的中心已不在目标身上, 到40帧时, 跟踪失败。本文的算法结合了颜色、边缘和纹理3个特征, 能够使矩形框的中心稳定在目标中心的周围。图2(b)中第90帧里出现了干扰物, 第290帧里目标被干扰物遮挡, 第480帧里目标所处环境变得复杂, 跟踪结果显示, 基于多特征融合的跟踪具有较强的鲁棒性, 能够满足跟踪要求。

实验2 选取较为复杂的人脸作为跟踪目标来验证特征权值的自适应对跟踪性能的影响。图3(a)为文献[3]固定权值的跟踪结果, 第244帧和第310帧分别是身体发生转动和头部发生转动的画面, 目标的颜色和边缘都发生了变化, 如果权值仍保持不变, 则跟踪效果不理想, 甚至会失败。本文的多特征自适应权值可以很好地解决这一问题。

图3 人脸跟踪实验Fig.3 Face tracking experiment

图3(c)给出了两种跟踪算法结果的误差对比, 可以看出, 使用固定权值的跟踪算法具有较大的误差。在目标旋转、缩小、被遮挡时, 文献[3]算法很难满足精度要求。本文所提的算法能够保证跟踪误差在一定的范围内, 可以有效提高跟踪的稳定性。图3(d)给出了粒子的数量随帧数的变化曲线, 可以看出, 当跟踪误差较大时, 粒子数量会自适应增加来响应跟踪误差。

表1为文献[3]算法和本文算法平均耗时对比表, 由表中数据可知:本文算法的粒子数不是固定的, 可随着背景的复杂程度变化而变化, 所以平均耗时较少。而在文献[3]算法中, 由于粒子数固定, 当场景中的背景变简单时, 算法的效率会降低, 耗时增加。

表1 算法平均每帧耗时对比 Table 1 Comparison of each frame’ s time-consuming
5 结束语

提出了一种基于多特征融合的自适应粒子滤波算法, 将目标的颜色、边缘和纹理特征引入到粒子滤波中。实验表明:在非高斯非线性的环境中, 该算法能避免单一特征以及固定权值跟踪中的不足, 有效地解决了目标旋转、目标遮挡以及背景混淆等诸多问题, 具有较高的鲁棒性。当视频序列的尺寸较大或者背景较复杂需要数量较多的粒子时, 算法处理的时间较长, 会导致实时性变差。所以, 如何提高粒子的质量来减少粒子的数量是下一步将要研究的问题。

The authors have declared that no competing interests exist.

参考文献
[1] 叶龙, 王京玲, 张勤. 遗传重采样粒子滤波器[J]. 自动化学报, 2007, 33(8) : 885-887.
Ye Long, Wang Jing-ling, Zhang Qin. Genetic resampling particle filter[J]. Acta Automatica Sinica, 2007, 33(8): 885-887. [本文引用:1] [CJCR: 0.572]
[2] Wang Zhao-wen, Yang Xiao-kang, Xu Yi, et al . CamShift guided particle filter for visual tracking[J]. Pattern Recognition Letters (S0167-8655), 2009, 30(4): 407-413. [本文引用:1]
[3] 高秀斌, 丁盼盼, 蒋长帅, 等. 一种基于多特征融合的粒子滤波目标跟踪算法[J]. 扬州大学学报: 自然科学版, 2013, 16(1): 57-60.
Gao Xiu-bin, Ding Pan-pan, Jiang Chang-shuai, et al. A particle filter algorithm for objects tracking based on multi-feature fusion[J]. Journal of Yangzhou University(Natural Science Edition), 2013, 16(1): 57-60. [本文引用:1] [CJCR: 0.3067]
[4] Kwok C, Fox D, Meil A M. Adaptive real-time particle filters for robot localization[C]∥IEEE International Conference on Robotics and Automation. USA: IEEE Press, 2003: 2836-2841. [本文引用:1]
[5] Bolic M, Djuric P M, Hong S. Resampling algorithms for particle filters: a computational complexity perspective[J]. Eurasip Journal on Applied Signal Processing (S1687-0433), 2004, 15(15): 2267-2277. [本文引用:1]
[6] Bolic M, Djuric P M, Hong S. Resampling algorithms and architectures for distributed particle filter[J]. IEEE Transaction on Signal Processing (S1053-587X), 2005, 53(7): 2442-2450. [本文引用:1]
[7] 胡士强, 敬忠良. 粒子滤波原理及其应用[M]. 北京: 科学出版社, 2010: 21-23. [本文引用:1]
[8] 刘士荣, 朱伟涛, 杨帆, 等. 基于多特征融合的粒子滤波目标跟踪算法[J]. 信息与控制, 2012, 41(6): 752-759.
Liu Shi-rong, Zhu Wei-tao, Yang Fan, et al. Multi-feature fusion based particle filter algorithm for object tracking[J]. Information and Control, 2012, 41(6): 752-759. [本文引用:1] [CJCR: 0.669]
[9] Comaniciu D, Ramesh V, Meer P. Kernel-based object tracking[J]. IEEE Trans on Pattern Analysis and Machine Intelligence (S0162-8828), 2003, 25(5): 564-577. [本文引用:1]
[10] Katja N, Esther K M. Object tracking with an adaptive color-based particle filter[C]∥Proceedings of the 24th DAGM Symposium on Pattern Recognition, Zurich, 2002: 353-360. [本文引用:1]