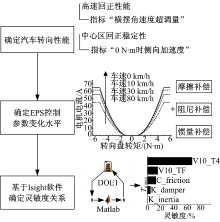
仿真研究EPS系统参数与车辆转向性能的关系。基于Matlab/Simulink搭建EPS系统模型, 车辆模型采用Carsim商用软件, 从而建立EPS系统与车辆模型联合仿真平台, 如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 EPS系统模型与Carsim联合仿真平台Fig.1 Co-simulink platform for EPS system model and Carsim model

EPS系统模型输入为左右车轮的轮胎力和车轮定位参数, 输出为左右车轮的转向角。Carsim车辆模型的输入为左右转向车轮的转向角, 输出为轮胎力和车轮定位参数。通过调整EPS系统参数, 进行Simulink与Carsim的联合仿真。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 灵敏度分析方案Fig.2 Scheme of sensitivity analysis

灵敏度分析方案如图2所示。首先转向性能评价指标为高速回正性能指标“ 横摆角速度超调量” 及中心区回正稳定性能评价指标“ 0 N· m时侧向加速度” 。其次, 确定进行灵敏度分析的EPS系统参数包括助力特性参数和系统补偿参数, 并定义系统参数的3个变化水平值。最后, 基于Isight软件设计EPS系统参数的正交试验表, 并通过Matlab与Carsim联合模型进行仿真试验, 计算每组正交试验下的指标值, 然后采用极差分析法确定EPS系统参数与转向性能的灵敏度关系。

助力曲线为多点折线拟合曲线特性, 助力特征点的确定参照文献[9], 助力死区和助力饱和区临界转向盘力矩分别为1 N· m和5 N· m。随着助力特征点数量的增多, 助力特性会逐步接近理想的曲线型助力效果, 但会导致调试工作量增大。对于本文的灵敏度分析方法, 不同的特征点数量只会导致程序运算量存在差异, 故将助力特性曲线转矩间隔定义为1 N· m。既能获得近似于曲线型的助力特性, 又能减少调试工作量, 提高灵敏度分析时的程序运算效率。

通过统计5款以上A级对标车的操纵稳定性试验数据, 转向轻便区和强路感区的分界值是3 N· m。Ⅰ 区为助力死区(0~1 N· m), Ⅱ 区为强路感区(1~3 N· m), Ⅲ 区为转向轻便区(3~5 N· m), 5 N· m以上为助力饱和区, 如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 EPS助力特性曲线区域Fig.3 Areas for the power characteristic curve of EPS

在进行高速回正性能试验时, 转向盘转矩基本为0 N· m, 故定义100 km/h车速下的助力曲线上的助力死区临界转向盘转矩值为灵敏度分析参数。根据EPS调试经验, 助力死区的临界转向盘转矩基准值设定为1 N· m, 另外两个水平值分别设定为0.5 N· m和1.5 N· m。

在进行中心区连续正弦试验时, 转向盘力矩不超过4 N· m, 故只需考察100 km/h下助力死区Ⅰ 和强路感区Ⅱ 的助力特性参数。根据各参数的实际取值范围, 定义各特性参数水平值如表1所示。

表1

Table 1

表1(Table 1)

表1 助力特性参数水平值 Table 1 Levels of power characteristic parameters 助力特性参数 基准值 偏小水平值 偏大水平值 助力死区值/(N· m) 1.0 0.5 1.5 2 N· m助力电流值/A 4.5 0.0 10.5 3 N· m助力电流值/A 13.5 11.0 21.0

表1 助力特性参数水平值 Table 1 Levels of power characteristic parameters

EPS系统补偿参数包括惯量补偿系数、阻尼补偿系数和摩擦补偿电流。系数值以完全克服转向系统的惯性力矩、阻尼阻力矩和摩擦阻力矩为依据来确定, 并取最大值。通过在K& C试验台上对某EPS试验车的多次测量, 得到转向系统的惯性力矩、阻尼阻力矩和摩擦阻力矩的统计值分别为0.107 kg· m²、0.29 N· m(rad/s)、3.62 N· m。然后根据实车调试经验在变化范围内定义了系统补偿参数的基准值, 经过计算得到各个系统补偿参数的偏小水平值和偏大水平值, 如表2所示。

表2

Table 2

表2(Table 2)

表2 系统补偿参数水平值 Table 2 Levels of system compensation parameters 系统补偿参数 基准值 偏小水平值 偏大水平值 惯量补偿系数 /(A· rad-1· s2) 0.05 0 0.09 阻尼补偿系数 /(A· rad-1· s) 0.15 0 0.25 摩擦补偿电流/A 2.00 0 3.10

表2 系统补偿参数水平值 Table 2 Levels of system compensation parameters

Isight软件旨在解决在产品设计中, 设计参数多、运行环境复杂、性能指标相互制约等问题, 能够快速分析出参数的敏感性, 并能进行品质优化^[10]。它能代替工程人员处理重复性强、易出错的数字处理及设计工作^[11]。

正交试验设计通过正交表的方式考虑多因素、多水平的影响, 应用统计学方法如极差分析方法、方差分析方法等对试验结果进行分析^{[12, 13, 14]}。

本文采用正交设计极差分析方法, 对EPS系统参数与转向性能的灵敏度进行分析。该灵敏度关系体现的是系统参数变化对转向性能指标的相对影响关系, 而非绝对关系。但该方法能使各参数、各水平分布均匀, 试验次数减少, 从而有效地提高试验效率。同时在每组正交系统参数下, 易于对灵敏度分析结果进行实车试验验证。

正交试验正交表定义为L_N(Q^M), N为试验次数, M为系统参数数量, Q为每个参数的水平值数量。以3个系统参数为例, 每个系统参数取3个变化水平值, 正交试验设计正交表为L₉(3³), 如表3所示。V1、V2、V3为3个变化水平值, V2为基准值, V1为偏小水平值, V3为偏大水平值。

表3

Table 3

表3(Table 3)

表3 L9(33)正交表设计 Table 3 Orthogonal design table for L9(33) 试验次数 参数1 参数2 参数3 1 V1 V1 V1 2 V1 V2 V2 3 V1 V3 V3 4 V2 V1 V2 5 V2 V2 V3 6 V2 V3 V1 7 V3 V1 V3 8 V3 V2 V1 9 V3 V3 V2

表3 L9(33)正交表设计 Table 3 Orthogonal design table for L9(33)

EPS系统参数与“ 横摆角速度超调量” 、“ 0 N· m时的侧向加速度” 的灵敏度关系如图4、图5所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
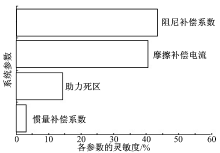	图4 系统参数与横摆角速度超调量的灵敏度关系Fig.4 Sensitivity relationship between system parameters and yaw rate overshoot

图5

Fig.5

	Figure Option ViewDownloadNew Window
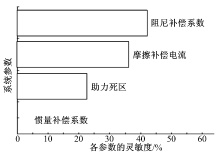	图5 系统参数与0 N· m时侧向加速度的灵敏度关系Fig.5 Sensitivity relationship between system parameters and lateral acceleration at 0 N· m

由图4可知, 阻尼补偿系数和摩擦补偿电流与横摆角速度超调量具有较大的灵敏度关系, 助力死区的转向盘力矩和惯性补偿系数具有相对较弱的敏感性, 为次要的影响参数。

由图5可知, 0 N· m时侧向加速度与横摆角速度超调量具有相同的影响参数, 助力死区为次要影响参数, 惯量补偿系数的敏感度几乎为零, 可以忽略。

本文取对转向性能影响力较高的前两位影响参数, 即阻尼补偿系数和摩擦补偿电流。对比图4和图5两幅图可知, 两个指标与系统参数之间的敏感性程度相似。两个指标的相关性系数为-0.88, 说明两个指标具有较大的负相关性, 即调试系统参数使指标“ 横摆角速度超调量” 减小, 而指标“ 0 N· m时侧向加速度” 会增大。

从系统动力学角度分析以上影响关系如下:

(1)0 N· m时侧向加速度表征了转向盘转向中间位置过程中, 转向盘力矩为零, 即回正力矩等于系统阻力矩时的侧向加速度值。回正力矩包括系统结构回正力矩和系统补偿回正力矩, 系统阻力矩包括摩擦阻力矩、阻尼阻力矩和惯性阻力矩, 在中心区附近, 由于转向盘角加速度较小, 惯性阻力矩基本为零, 摩擦阻力矩基本恒定, 阻尼阻力矩随转向盘转速降低而减小。相同角速度下, 当增大阻尼补偿系数和摩擦补偿电流时, 系统补偿回正力矩变大, 摩擦阻力矩和阻尼阻力矩基本不变, 故只有系统结构回正力矩值更小, 即更接近转向盘中间位置时, 转向系统回正力矩值才会收敛并等于系统阻力矩。即转向盘力矩零点对应的位置更接近转向盘中间位置, 该点的侧向加速度值也趋于零。

(2)横摆角速度超调量表征了转向盘转至并稳定到中间位置过程中, 横摆角速度的最大震荡程度。高速回正试验中, 转向盘力矩为零, 回正力矩克服系统阻力矩使转向盘回到中间位置。回正力矩成分同样包括系统结构回正力矩和系统补偿回正力矩。当增大阻尼补偿系数和摩擦补偿电流时, 系统补偿回正力矩增大, 导致转向盘回正角速度变大。转向盘转过中间位置后, 系统结构回正力矩与系统阻力矩同向, 并克服系统补偿回正力矩使转向盘角速度减小。当角速度等于零时, 转向盘开始转向中间位置。故增大的系统补偿回正力矩, 需要更大的系统结构回正力矩克服补偿回正力矩及惯性, 结构回正力矩值随转向盘至中间位置的距离增加而增加, 从而导致超调量增大。

基于永磁同步电机EPS开发原型控制器, 并基于国内某品牌车开发了EPS试验车。以该车为试验平台, 改变阻尼补偿系数和摩擦补偿电流值, 先后取基准值、偏小变化水平值、偏大变化水平值进行高速回正性能试验和中心区正弦试验。

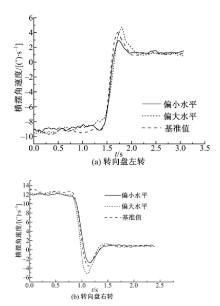
高速回正试验工况:以车速100 km/h直线行驶, 转动转向盘使侧向加速度达到2 m/s², 稳定数秒后撒手回正。记录横摆角速度时间历程曲线, 如图6所示。经数据处理程序得到指标“ 横摆角速度超调量” 值, 如表4所示。

表4

Table 4

表4(Table 4)

表4 高速回正性能试验指标 Table 4 Indice of high-speed returnability test % 转动方向 超调量 基准值 偏小水平值 偏大水平值 左转 横摆角速度 17.4 13.2 19.1 右转 横摆角速度 17.2 16.5 22.4

表4 高速回正性能试验指标 Table 4 Indice of high-speed returnability test %

中心区正弦试验工况:以车速100 km/h直线行驶, 转向盘转动频率0.2(100%± 10%)Hz, 幅值变化符合正弦曲线, 峰值使侧向加速度为2 m/s²。记录数据转向盘转矩和侧向加速度, 并画出转向盘转矩相对侧向加速度曲线, 如图5所示。通过数据处理程序得到指标“ 0 N· m时侧向加速度” 的偏大水平值、偏小水平值、基准值分别为0.52、1.04、0.68 m/s²。

由图6(a)(b)中左右方向横摆角速度的时间历程曲线可知, 在高速回正状态下, 当阻尼补偿系数和摩擦补偿电流取值依次为偏小水平值、基准值、偏大水平值时, 横摆角速度超调量有明显增大的趋势。通过实验数据处理得到的指标“ 横摆角速度超调量” 也证明了横摆角速度超调量对系统的两个参数变化的响应趋势。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 高速回正时横摆角速度对比曲线Fig.6 Correlation curve of yaw rate on high-speed returnability condition

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 中心区转向盘转矩与侧向加速度关系曲线Fig.7 On-center correlation curve of steering-wheel torque and lateral acceleration

由图7中转向盘转矩与侧向加速度曲线可知, 当阻尼补偿系数和摩擦补偿电流的取值增大时, 曲线与横轴交点的绝对值有明显变小的趋势, 即转向盘转矩为0 N· m时所对应的的侧向加速度减小, 转向盘也就越接近中间位置。4.1节中指标“ 0 N· m时侧向加速度” 也证明了该指标对阻尼补偿系数和摩擦补偿电流的响应趋势。

由于实车试验中存在着噪声等干扰, 故试验曲线会存在一定的失真, 没有反应出真实的响应量。但对比曲线及指标给出的变化规律验证了系统参数的改变与性能指标之间的响应特性, 以及两个指标之间的相关性关系。