永磁式缓速器的制动力矩分级结构设计

引用本文

何仁, 王晶, 胡东海. 永磁式缓速器的制动力矩分级结构设计. 2015, 45(4): 1056-1062
HE Ren, WANG Jing, HU Dong-hai. Design of braking torque graded structures of permanent magnet retarder. Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1056-1062 复制到剪切板

Permissions

永磁式缓速器的制动力矩分级结构设计

何仁, 王晶, 胡东海

江苏大学汽车与交通工程学院,江苏镇江 212013

作者简介:何仁(1962-)男,教授,博士生导师.研究方向:汽车机电一体化技术.E-mail:heren@mail.ujs.edu.cn

基金:2011年江苏省苏北科技发展计划项目(BC2011446)

摘要

为分析永磁式缓速器制动力矩的影响因素,设计了制动力矩可以分级的永磁式缓速器,运用解析法对永磁式缓速器的气隙磁场建立数学模型,通过分离变量法结合边界条件,获得了气隙磁通密度的表达式。再运用源和场理论推导出适合工程应用的永磁式缓速器制动力矩计算公式。在此基础上分析了磁极对数、永磁体周向宽度、永磁体轴向长度和气隙大小对气隙磁场和制动力矩的影响,并分别根据这4种参数,设计了4种可行的制动力矩分级结构。

关键词: 车辆工程; 缓速器; 制动力矩分级; 气隙磁通密度; 结构设计

中图分类号:U463.5 文献标志码:A 文章编号:1671-5497(2015)04-1056-07

Design of braking torque graded structures of permanent magnet retarder

HE Ren, WANG Jing, HU Dong-hai

School of Automobile and Traffic Engineering, Jiangsu University, Zhenjiang 212013,China

Abstract

To design the braking torque graded permanent magnet retarder, the rules of the factors that influence the braking torque retarder must be understood. In this paper, the mathematical model of the air-gap of magnetic field was established by means of analytic method. Using variable separation method and boundary conditions, the analytical expression of the magnetic induction intensity of the air-gap was obtained. According to the source and field theory, the computation model of braking torque, applicable to engineering application, was derived. The impacts of the number of magnetic pole pairs, the perimetric width and axial length of the permanent magnet, and the air-gap on the magnetic induction intensity and on the braking torque were analyzed based on the computation model. Based on the four parameters, four types of graded braking torque structures of the permanent magnet retarder were designed.

Keyword: vehicle engineering; retarder; braking torque graded; magnetic induction intensity; structure design

Show Figures

0 引言

永磁式缓速器是一种节能型辅助制动装置, 其安装维护简单, 结构尺寸小, 质量轻, 几乎不消耗电力, 连续使用自身不会产生过热, 能持续不断地保持制动力的稳定性和持久性, 在高速范围内制动力也不会过多降低, 且传动轴转速越高, 制动力越大等^{[1, 2, 3]}, 具有很好的市场应用前景。目前使用中的永磁式缓速器还存在一些不足, 较为突出的问题是永磁式缓速器不能根据路况或车速分档调节制动力矩^[4]。它只有两种工作状态:制动和非制动状态, 当驾驶员进行制动时, 车辆由运行状态突然切入到一个较大的制动状态, 产生一个较大的减速度, 使驾驶员产生类似急刹车的不良的制动感觉。如果永磁式缓速器能够实现制动力矩分级, 并且像电涡流缓速器一样将制动力矩分为多档, 让驾驶者根据不同路面环境和车速情况选择缓速器工作输出制动力矩的大小, 将会有更大的市场竞争力。因此不少学者在致力于研究永磁式缓速器制动力矩分级技术。2005年3月江苏大学何仁教授等^[5]申请了一种分级控制永磁式缓速器发明专利, 它是在磁铁周向转动式永磁缓速器结构基础上进行改进的, 主要在定子上再增加了一列永久磁铁来达到制动力矩分级和减少漏磁的目的。同一时间, 江苏大学何仁教授等^[6]还申请了一种制动力矩可分档的永久磁铁式缓速器专利, 它是通过改变磁铁周向转动式永磁缓速器上固定和活动磁极的分布, 设计出1/2最大制动力矩的档位。2010年2月北京工业大学李德胜教授等^[7]申请了转子冷却式汽车永磁液冷缓速器发明专利, 气缸通过轴承可以推动转子, 移动转子可改变永久磁铁与定子之间的相交面积的大小, 从而实现永磁式缓速器制动力矩的分级分档或连续调节。北京工业大学叶乐志在其学位论文中提出了独立磁头的方法^[8], 即每块永久磁铁由独立的气缸活塞机构控制, 可以独立地变化工作状态, 其结构与电涡流缓速器相似, 通过控制参与制动工作的磁头对数改变制动力矩的大小。

在国外, 永磁式缓速器已经产品化, 外国学者研究重点主要在理论分析与设计研究方面。日本冈山大学的Muramatsu等^[9]运用移动坐标系对永磁缓速器进行了3D直流稳态涡流分析。Natsumeda等^[10]将有限元同Rosenbrock’ s方法用于永磁式缓速器的三维优化设计。值得一提的是美国德克萨斯州农工大学的Gay等^{[11, 12]}设计了一种摩擦制动器和永磁缓速器联合制动方案, 并对联合制动器应用于传统汽车和混合动力汽车上的效果和影响进行了分析。论文中虽然没有涉及到具体的永磁式缓速器制动力矩分级方法, 但是永磁缓速器若能实现制动力矩分级, 这种联合制动方式必定能更好地运用于复杂的行车工况。

本文运用解析法推导了永磁式缓速器气隙磁通密度的计算公式, 并运用源和场理论计算制动力矩。在此基础上讨论磁极对数、永磁体周向宽度、永磁体轴向长度和气隙大小对缓速器气隙磁场和制动力矩的影响, 并根据分析结果提出了4种可行的永磁式缓速器制动力矩分级结构, 为分级式永磁缓速器的设计提供了依据。

1 永磁式缓速器的工作原理

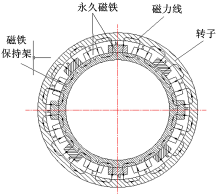
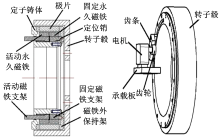
永磁式缓速器的基本工作原理是:利用电磁原理把汽车行驶的动能转化为热能而散发掉, 从而实现汽车的减速和制动^[13]。永磁式缓速器制动力矩的产生过程是:需要制动时, 在驱动装置的推动下, 永久磁铁进入工作位置, 产生的磁场在永磁体、气隙、转子毂和磁铁保持架之间构成回路, 如图1所示。这时转子毂内部有无数个闭合导线所包围的面积内的磁通量在发生变化, 从而在转子毂内部产生无数涡旋状的涡流。涡流产生后, 磁场就会对带电的转子毂产生阻止其转动的阻力, 阻力的方向可由弗莱明左手法则来判断, 阻力的合力沿转子毂周向形成与其旋转方向相反的制动力矩。

	Figure Option View Download New Window
	图1 永磁式缓速器工作原理示意图Fig.1 Schematic diagram of permanent magnet retarder

2 气隙磁场的分析计算

在对气隙磁场进行分析时, 可供选择的方法有解析法^{[14, 15]}和有限元法^[16]。

根据永磁式缓速器的工作原理, 转子是与传动轴相连, 随着传动轴一起旋转的, 一般不能设置机构来改变转子参数。因此, 在转子参数(尺寸和材料参数)确定的情况下, 要改变输出制动力矩的大小, 只有通过改变参与制动作用的定子参数, 从而改变气隙磁通密度来实现制动力矩的调节。

气隙磁通密度并非常数。严格意义上讲, 不同点的磁通密度不同, 而且随着转速变化, 同一点的磁通密度也发生变化。本文主要探讨的是改变定子参数对永磁式缓速器制动力矩的影响, 因此不考虑转速对磁通密度的影响。

基于以上两点, 本文选用解析法对气隙磁通密度求解, 使用了分离变量法结合边界条件和连续性条件对微分方程进行求解, 求解的位函数采用标量磁位。

2.1 气隙磁场的解析模型

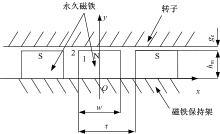
图2为永磁式缓速器气隙磁场的解析模型, 图中1为永磁区域, 2为气隙区域, w为永磁体的周向宽度, g_e为气隙, h_m为永磁体的高度, τ 为相邻永久磁铁的极距。

	Figure Option View Download New Window
	图2 永磁式缓速器的解析模型Fig.2 Analytical model of permanent magnet retarder

2.2 气隙磁场的求解

将永磁体和气隙区域设为求解区域。求解区域电流密度为0, 为无旋场, 有:

$\begin{matrix} H = - \nabla φ (1) \end{matrix}$

由麦克斯韦方程组可知:

$\begin{matrix} \nabla \cdot B = 0 (2) \end{matrix}$

在气隙和永磁区域中磁通密度可以表示为:

$\begin{matrix} \{\begin{matrix} B_{1} = μ_{0} μ_{r} H + μ_{0} M \\ B_{2} = μ_{0} H \end{matrix} (3) \end{matrix}$

式中:B₁为永磁区域磁通密度; B₂为气隙区域磁通密度; μ ₀为真空磁导率, N/A²; μ _r为相对磁导率; M为永磁体磁化强度; H为磁场强度。

从而可知, 在二维坐标系下标量磁势满足:

$\begin{matrix} \{\begin{matrix} \frac{\partial^{2} φ_{1}}{\partial x^{2}} + \frac{\partial^{2} φ_{1}}{\partial y^{2}} = \frac{\nabla \cdot M}{μ_{r}} \\ \frac{\partial^{2} φ_{2}}{\partial x^{2}} + \frac{\partial^{2} φ_{2}}{\partial y^{2}} = 0 \end{matrix} (4) \end{matrix}$

式中:φ ₁为永磁区域标量磁势; φ ₂为气隙区域标量磁势。

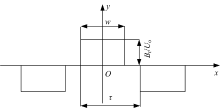
永磁体磁化强度分布如图3所示。

	Figure Option View Download New Window
	图3 磁化强度分布Fig.3 Dstribution of magnetization

将磁化强度M用傅立叶级数展开, 得:

$\begin{matrix} M = \frac{4 B_{r}}{μ_{0} π} \overset{\infty}{\sum_{i = 1, 3, 5, \dots}} \sin (\frac{iπw}{2 τ}) \cos (\frac{iπ}{τ} x) (5) \end{matrix}$

式中:B_r为永久磁铁剩磁, 单位为T; τ =π r₁/N_p, 其中r₁为磁铁保持架的外径, N_p为磁极对数。

利用分离变量法解拉普拉斯方程, 得式(4)的通解为:

$\begin{matrix} \begin{matrix} φ = \overset{\infty}{\sum_{i = 1, 3, 5, \dots}} [A_{1} s inh (\frac{iπ}{τ} y) + \\ A_{2} \cosh (\frac{iπ}{τ} y)] \cos (\frac{iπ}{τ} x) (6) \end{matrix} \end{matrix}$

式中:A₁、A₂为待定系数。

根据建立的永磁式缓速器气隙磁场的数学模型, 有如下边界条件:

$\begin{matrix} \{\begin{matrix} φ_{2} (x, y) |_{y = h_{m} + g_{e}} = 0 \\ φ_{2} (x, y) |_{y = h_{m}} = φ_{1} (x, y) |_{y = h_{m}} \\ B_{2 y} (x, y) |_{y = h_{m}} = B_{1 y} (x, y) |_{y = h_{m}} \end{matrix} (7) \end{matrix}$

由边界条件(7)与通解(6)联立, 就可以得到气隙区域任何位置的磁通密度B₂_y:

$\begin{matrix} \begin{matrix} B_{2 y} = \frac{4 B_{r}}{π} \overset{\infty}{\sum_{i = 1, 3, 5, \dots}} \frac{\cosh [i N_{p} \frac{g_{e} + h_{m} - y}{r_{1}}]}{isinh [i N_{p} \frac{g_{e} + h_{m}}{r_{1}}]} \\ \sin (\frac{i N_{p} w}{2 r_{1}}) \sinh (\frac{i N_{p} h_{m}}{r_{1}}) \cos (\frac{i N_{p}}{r_{1}} x) (8) \end{matrix} \end{matrix}$

当y=g_e+h_m时, 可以得到转子表面的气隙磁通密度:

$\begin{matrix} \begin{matrix} B_{2} |_{g_{e} + h_{m}} = \\ \frac{4 B_{r}}{π} \overset{\infty}{\sum_{i = 1, 3, 5, \dots}} \frac{\sin (\frac{iw N_{p}}{2 r_{1}}) \sinh (\frac{i h_{m} N_{p}}{r_{1}})}{isinh [\frac{i N_{p} (g_{e} + h_{m})}{r_{1}}]} \cos (\frac{i N_{p}}{r_{1}} x) (9) \end{matrix} \end{matrix}$

2.3 平均气隙磁通密度的计算

采用解析法来推导气隙磁通密度的表达式, 计算出平均气隙磁通密度, 将工作气隙中空间上不均匀分布的气隙磁场化成等值的均匀磁场处理。根据式(9), 得到平均气隙磁通密度B为:

$\begin{matrix} \begin{matrix} B = \\ \frac{\int_{0}^{2} |\frac{4 B_{r}}{π} \overset{\infty}{\sum_{i = 1, 3, 5}} \frac{\sin (\frac{iw N_{p}}{2 R}) \sinh (\frac{i h_{m} N_{p}}{R})}{isinh [\frac{i N_{p} (g_{e} + h_{m})}{R}]} \cos (\frac{i N_{p}}{R} x)| dx}{2 πR} (10) \end{matrix} \end{matrix}$

3 缓速器制动力矩的计算

本文采用源和场理论计算模型计算制动力矩。

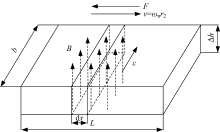
计算模型如图4所示^[17], L为以转子毂内径r₂为半径的等效周长, L=2π r₂, b为永磁铁轴向长度, 垂直穿过转子毂的磁通密度为B, 转子毂的旋转角速度为ω _n。为了简化计算过程, 作如下假设:①转子毂中的电涡流仅沿宽度方向, 且在整个转子毂上的涡电流密度相同; ②认为转子材料的电导率、磁导率为常数。

	Figure Option View Download New Window
	图4 计算模型示意图Fig.4 Schematic diagram of computational model

如图4的计算模型所示, 转子毂的速度v、磁通密度B、电动势ε 三者的方向相互垂直, 取微元dx, 微元的感应电动势为:

$\begin{matrix} ε = bvB (11) \end{matrix}$

式中:v=ω _nr₂, ω _n=2π n/60, 其中ω _n为转子毂转动的角速度, 单位为rad/s, n为转子转速, 单位为r/min。

微元部分的瞬时功率为:

$\begin{matrix} dp = \frac{ε^{2}}{dR} = \frac{B^{2} {ω_{n}}^{2} {r_{2}}^{2} b}{ρ} Δhdx (12) \end{matrix}$

式中:ρ 为转子鼓的电阻率, 单位为Ω · m; Δ h为集肤深度, Δ h= $\begin{matrix} \sqrt[]{\frac{2}{σ μ_{r} N_{p} ω_{n}}} \end{matrix}$ , 单位为m; b为永久磁铁的轴向长度; σ 为转子鼓的电导率, 单位为S/m; μ _r为转子材料的相对磁导率; N_p为磁极对数。

转子毂的制动功率为:

$\begin{matrix} P = \int_{0}^{2} d p = \frac{2 π B^{2} {ω_{n}}^{2} {r_{2}}^{3} bΔh}{ρ} (13) \end{matrix}$

因此制动力矩为:

$\begin{matrix} T = \frac{P}{ω_{n}} = \frac{2 π B^{2} ω_{n} {r_{2}}^{3} bΔh}{ρ} (14) \end{matrix}$

将式(10)带入式(14)得到制动力矩的计算式(15):

$\begin{matrix} \{\begin{matrix} T = \frac{P}{ω_{n}} = \frac{2 π B^{2} ω_{n} {r_{2}}^{3} bΔh}{ρ} \\ B = \frac{\int_{0}^{2} |\frac{4 B_{r}}{π} \overset{\infty}{\sum_{i = 1, 3, 5}} \frac{\sin (\frac{iw N_{p}}{2 R}) \sinh (\frac{i h_{m} N_{p}}{R})}{isinh [\frac{i N_{p} (g_{e} + h_{m})}{R}]} \cos (\frac{i N_{p}}{R} x)| dx}{2 πR} \end{matrix} (15) \end{matrix}$

4 缓速器制动力矩影响因素分析

根据式(15)可以得出永磁式缓速器制动力矩大小与永磁体的剩磁大小B_r、磁极对数N_p、永磁体高度h_m、永磁体周向宽度w、永磁体轴向长度b, 转子的相对磁导率μ _r、电导率σ 、角速度ω _n、磁铁保持架半径r₁、气隙大小g_e有关。

当永磁式缓速器结构设计完成时, 永磁体的剩磁大小B_r、永磁体高度h_m、转子相对磁导率μ _r、电导率σ 、磁铁保持架半径r₁等参数就确定下来。在转速一定的情况下, 可以改变的参数就是参与工作的永磁体周向宽度w、轴向长度b以及磁极对数N_p和气隙大小g_e。

4.1 磁极对数N_p的影响

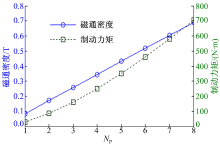
磁通密度、制动力矩与磁极对数的关系如图5所示。磁通密度与磁极对数呈线性关系, 且斜率为正值, 随着磁极对数的增加, 磁通密度增大。从图5还可看出:随着磁极对数的增加, 制动力矩也随之变大。但是, 制动力矩与磁极对数并不是线性关系, 例如, 8对磁极时, 制动力矩约为706 N· m; 4对磁极时, 制动力矩约为270 N· m, 约为8对磁极时制动力矩的38%。

	Figure Option View Download New Window
	图5 磁通密度、制动力矩与磁极对数的关系Fig.5 Relationship between magnetic induction intensity, braking torque and number of polepairs

4.2 永磁体周向宽度w的影响

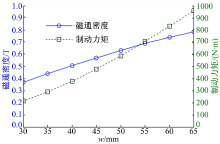
磁通密度、制动力矩与永磁体宽度的关系如图6所示, 磁通密度、制动力矩与永磁体宽度近似呈线性关系, 且斜率为正值, 随着永磁体宽度的增加, 磁通密度、制动力矩相应地变大, 与文献[18]中的分析结果一致。

	Figure Option View Download New Window
	图6 磁通密度、制动力矩与永磁体宽度的关系Fig.6 Relationship between magnetic induction intensity, braking torque and width of pole

4.3 气隙大小g_e的影响

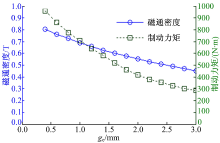
磁通密度、制动力矩与气隙大小的关系如图7所示, 磁通密度、制动力矩与气隙大小近似呈线性关系, 且斜率为负值, 磁通密度、制动力矩随着气隙大小的增大而减小, 与文献[18]的分析结果一致。

	Figure Option View Download New Window
	图7 磁通密度、制动力矩与气隙大小的关系Fig.7 Relationship between magnetic induction intensity, braking torque and length of air-gap

4.4 永磁体轴向长度b的影响

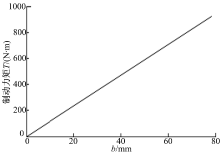
从式(9)看出, 本文采用的解析法计算气隙磁通密度, 是对空间内二维磁通密度进行分析计算, 因此没有涉及永磁体轴向长度b, 只在运用源和场理论计算制动力矩时出现永磁体轴向长度b这一项, 根据式(15), 制动力矩与永磁体轴向长度呈直线关系(见图8), 与文献[18]的分析结果一致。

	Figure Option View Download New Window
	图8 制动力矩与永磁体轴向长度的关系Fig.8 Relationship between magnetic induction intensity, braking torque and length of pole

5 永磁式缓速器制动力矩分级结构

本文介绍了4种永磁式缓速器制动力矩分级结构。

5.1 改变参与工作的磁极对数N_p(结构一)

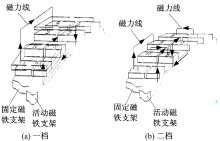
改变实际参与工作的磁极对数N_p, 江苏大学何仁教授设计如图9所示的结构^[6]。此结构改变了原先磁铁周向转动式永磁缓速器上磁极所用的N-S-N-S分布, 采用N-N-S-S的分布。在1档工作时, 实际参与工作的磁极对数只有2档的一半, 设计出1/2最大制动力矩的档位。

根据4.1节的分析结果, 此种结构1档时的制动力矩并没有达到2档时的一半, 并且采用这种结构, 制动力矩只能分为2档。

	Figure Option View Download New Window
	图9 分级式永磁缓速器的结构一Fig.9 First structure of braking torque graded of PMR

5.2 改变参与工作的永磁体周向宽度(结构二)

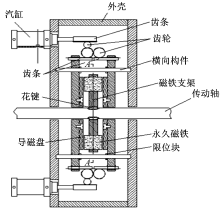
改变永磁体周向宽度w, 利用磁铁外保持架中非磁性材料的阻隔, 设计如图10所示的结构, 通过电机输出的角位移量, 控制活动磁铁支架及固定在其上的活动磁铁的旋转角度, 改变与固定永久磁铁的相对位置, 达到改变参与工作的永磁体宽度的效果, 从而实现制动力矩的变化。

	Figure Option View Download New Window
	图10 分级式永磁缓速器的结构二Fig.10 Second structure of braking torque graded of PMR

这种结构在设计时只需要改变齿轮机构的传动比, 就可以改变档位的数量, 在实际加工中易于实现。

根据4.2节的分析结果, 制动力矩和永磁体宽度之间近似呈线性关系, 在划分档位时可以平均分割活动磁铁支架的活动行程, 各个档位能提供的制动力矩大小存在确定的比例关系。

5.3 改变气隙大小g_e(结构三)

改变气隙大小, 设计如图11所示的分级式永磁缓速器结构。

	Figure Option View Download New Window
	图11 分级式永磁缓速器的结构三Fig.11 Third structure of braking torque graded of PMR

在此结构中, 气缸推动齿条运动, 经齿轮齿条啮合作用, 改变定子与转子之间气隙的大小, 改变气隙磁场分布, 实现制动力矩的变化。

根据4.3节的分析结果, 制动力矩与气隙大小近似呈线性关系, 通过气缸驱动, 可以实现制动力矩的无级调节。但由图7可见, 气隙微小的变化能够显著地影响制动力矩的大小, 因此采用这种制动力矩控制方法对零件加工的精度要求较高, 尤其对气缸活塞输出的行程精度要求很高。

5.4 改变参与工作永磁体轴向长度b(结构四)

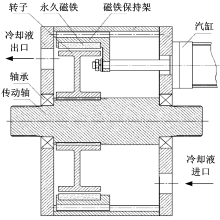
改变参与工作永磁体轴向长度, 北京工业大学李德胜教授设计如图12所示的结构^[7]。在此结构中, 转子通过花键与轴联结, 汽缸通过轴承可以推动转子, 移动转子可改变永久磁铁与定子之间的交集面, 即改变了参与制动工作的永磁体长度, 实现制动力矩变化。

	Figure Option View Download New Window
	图12 分级式永磁缓速器的结构四Fig.12 4th structure of braking torque graded of PMR

根据4.4节的分析结果, 制动力矩与永磁体轴向长度呈直线关系, 通过气缸驱动, 可以实现制动力矩的无级调节。但同时该结构气缸采用轴向布置的形式, 加大了永磁缓速器的轴向尺寸, 并且由气缸进行驱动, 缓速器起作用的时间比较长。

6 结论

(1)通过解析法对永磁式缓速器的气隙磁场进行数学建模, 以分析定子参数对气隙磁场的影响。通过分离变量法结合边界条件, 得到了气隙磁通密度的表达式。将工作气隙中空间上不均匀分布的气隙磁场化成等值的均匀磁场处理, 采用源和场理论建立永磁式缓速器制动力矩的计算模型, 推导出能够反映定子参数对制动力矩影响且计算量小, 适合工程应用的制动力矩计算公式。

(2)分析了磁极对数、永磁体周向宽度、永磁体轴向长度和气隙大小对气隙磁场和制动力矩的影响, 为分级式永磁缓速器的设计提供依据。结果表明, 气隙磁通密度、制动力矩随着磁极对数、永磁体周向宽度的增加而变大。永磁体轴向长度与制动力矩呈直线关系, 对气隙磁通密度没有影响。另一方面, 气隙磁通密度、制动力矩随着气隙的变大而减小。

(3)根据以上分析结果, 本文提供了4种可行的永磁式缓速器制动力矩分级结构, 为分级式永磁缓速器的设计提供参考。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	何仁. 汽车辅助制动装置[M]. 北京: 化学工业出版社, 2005: 116-123. [本文引用:1]
[2]	Kuwahara T, Araki K. Development of permanent magnet type eddy current retarder[J]. SAE Review, 1992, 13(1): 92-96. [本文引用:1]
[3]	朱宁, 王永华. 轻型永久磁铁式汽车缓速器[J]. 客车技术与研究, 2002, 24(4): 19-20. Zhu Ning, Wang Yong-hua. Lightweight permanent magnet retarder[J]. Bus Technology and Research, 2002, 24(4): 19-20. [本文引用:1]
[4]	牛润新. 车用永磁式缓速器设计理论与控制方法研究[D]. 镇江: 江苏大学汽车与交通工程学院, 2007. Niu Run-xin. Study on design theory and control method of permanent magnet type retarder in automobile[D]. Zhenjiang: School of Automobile and Traffic Engineering, Jiangsu University, 2007. [本文引用:1]
[5]	何仁, 牛润新, 胡青训. 一种分级控制永磁式缓速器[P]. 中国: 2005100379663, 2007-08-01. [本文引用:1]
[6]	何仁, 胡青训, 牛润新. 一种制动力矩可分档的永久磁铁式缓速器[P]. 中国: 2005200694593, 2006-07-19. [本文引用:2]
[7]	李德胜, 焦兵锋, 叶乐志, 等. 转子冷却式汽车永磁液冷缓速器[P]. 中国: 201110089667X. [本文引用:2]
[8]	叶乐志. 汽车永磁缓速器设计理论与试验研究[D]. 北京: 北京工业大学机械工程与应用电子技术学院, 2008. Ye Le-zhi. Optimization design research of automobile permanent magnet retarder[D]. Beijing: College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, 2008. [本文引用:1]
[9]	Muramatsu K, Takahash I N, Member S. 3D eddy current analysis in moving conductor of permanent magnet type of retarder using moving coordinate system[J]. IEEE Transactions on Energy Conversion, 1999, 14(4): 1312-1317. [本文引用:1]
[10]	Takahash I N, Natsumeda M, Muramatsu K. Optimization of permanent magnet type of retarder using 3D finite element method and direct search method[J]. IEEE Transactions on Magnetics, 1998, 34(5): 2996-2999. [本文引用:1]
[11]	Gay S E, Ehsani M. Optimized design of an integrated eddy-current and friction brake for automotive applications[C]∥IEEE Conference on Vehicle Power and Propulsion, IEEE, 2005: 290-294. [本文引用:1]
[12]	Gay S E, Ehsani M. Integration of eddy-current and friction brakes in conventional and hybrid vehicles[J]. SAE Transactions, 2005, 114(6): 3004-3018. [本文引用:1]
[13]	何仁, 赵万忠, 牛润新. 车用永磁式缓速器制动力矩的计算方法[J]. 交通运输工程学报, 2006, 6(4): 62-65. He Ren, Zhao Wan-zhong, Niu Run-xin. Braking torque computation method of permanent magnet retarder[J]. Journal of Transportation Engineering, 2006, 6(4): 62-65. [本文引用:1]
[14]	Aldo Canova, Bruno Vusini. Design of axial eddy-current couplers[J]. IEEE Transactions on Industry Applications, 2003, 39(3): 725-733. [本文引用:1]
[15]	Yao Y D, Chiou G J, Huang D R, et al. Theoretical computations for the torque of magnetic coupling[J]. IEEE Transactions on Magnetics, 1995, 31(3): 1881-1884. [本文引用:1]
[16]	Ye Le-zhi, Li De-sheng. Electromagnetic field analysis in permanent retarder based on finite element method[C]∥PIERS Proceedings, USA, 2010: 28-32. [本文引用:1]
[17]	何仁, 衣丰艳, 何建清. 电涡流缓速器制动力矩的计算方法[J]. 汽车工程, 2004(2): 197-200. He Ren, Yi Feng-yan, He Jian-qing. A computation method for braking torque of eddy current retarder[J]. Automobile Engineering, 2004(2): 197-200. [本文引用:1]
[18]	赵小波, 姬长英, 赵国柱. 永磁式涡流缓速器制动性能影响因素敏感性分析[J]. 农业机械学报, 2009, 40(10): 18-23. Zhao Xiao-bo, Ji Chang-ying, Zhao Guo-zhu. Sensitivity analysis on influence factors for braking performance of permanent magnet type eddy current retarder with uniform design[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(10): 18-23. [本文引用:1]

2005

0.0

... 0 引言永磁式缓速器是一种节能型辅助制动装置,其安装维护简单,结构尺寸小,质量轻,几乎不消耗电力,连续使用自身不会产生过热,能持续不断地保持制动力的稳定性和持久性,在高速范围内制动力也不会过多降低,且传动轴转速越高,制动力越大等^[1,2,3],具有很好的市场应用前景 ...

1992

0.0

2002

0.0

. 2002, 24(4):19-20 DOI:doi:10.3969/j.issn.1006-3331.2002.04.008

Lightweight permanent magnet retarder

轻型永久磁铁式汽车缓速器

Zhu Ning , Wang Yong-hua.

朱宁, 王永华

大型观光客车"GALA"是广州五十铃客车有限公司引进日本五十铃公司上世纪90年代末期的最新车型.该车采用了多种世界先进的技术和装备,永久磁铁式缓速器就是其中之一.

2007

0.0

. 2007, :-

Study on design theory and control method of permanent magnet type retarder in automobile

车用永磁式缓速器设计理论与控制方法研究[D]

Niu Run-xin.

牛润新

... 目前使用中的永磁式缓速器还存在一些不足,较为突出的问题是永磁式缓速器不能根据路况或车速分档调节制动力矩^[4] ...

2007

0.0

. 2007, :- DOI:doi:CN1329222C

一种分级控制永磁式缓速器

何仁, 牛润新, 胡青训

本发明涉及车用减速器，其能够根据路面情况的不同调节永磁式缓速器的档位，以实现提高制动力矩和提高安全性。 This invention relates to vehicle speed reducer according to different road conditions regulating permanent magnet retarder gear, in order to achieve improved braking torque and improved security. 本发明的特征在于定子增加一列固定的永磁铁，增加的一列永磁铁的块数、极数和排列与原来的一列固定磁铁完全相同；增加的一列永磁铁通过螺钉和定子的后轭板联接，原来的一列固定永磁铁则通过螺钉和固定磁铁支撑框联接。 The present invention is characterized in that the stator to increase a fixed permanent magnet, the increased a permanent magnet blocks, pole number and the arrangement of the original a fixed magnet are identical; increasing a permanent magnet by means of screws and the stator back yoke board connector, The original is a permanent magnet fixed by screws and the support frame fixed magnet coupling. 滑动磁铁依靠两组滚动轴承在固定磁铁支撑框上转动；在两列固定永磁铁之间和增加的永磁铁和磁性极片之间设有非磁性材料制成的屏蔽环。 Relying on two bearing slide magnet support frame in a fixed magnet is rotated; in between the two permanent magnets and the fixed permanent magnet and the increase between the magnetic pole pieces made of a non-magnetic shielding ring. 屏蔽环可以分别从径向和轴向撤出。 Shielding ring can be separately withdrawn from the radial and axial directions. 可实现分级控制的永磁式缓速器。 Can be realized hierarchical control of permanent magnet retarder.

... 2005年3月江苏大学何仁教授等^[5]申请了一种分级控制永磁式缓速器发明专利,它是在磁铁周向转动式永磁缓速器结构基础上进行改进的,主要在定子上再增加了一列永久磁铁来达到制动力矩分级和减少漏磁的目的 ...

2006

0.0

. 2006, :-

一种制动力矩可分档的永久磁铁式缓速器

何仁, 胡青训, 牛润新

永磁式缓速器是利用永久磁铁励磁从而获得车辆缓速效果的装置，是一种节能环保型辅助制动装置。但现有的永磁式缓速器所提供的制动力矩大小不能调节，很大程度制约了其应用。本学位论文主要目的是对分级式永磁缓速器结构设计方法进行研究，以期为国内开发具有自主知识产权的永磁式缓速器提供理论方法支持。　　首先，本文研究永磁式缓速器的工作机理、结构、性能特性，分析现有永磁式缓速器应用和发展状况，继而提出分级式永磁缓速器这一新的概念，并分析开发分级式永磁缓速器的必要性。　　其次，建立永磁式缓速器的数学模型，运用解析法推导出气隙磁通... 展开永磁式缓速器是利用永久磁铁励磁从而获得车辆缓速效果的装置，是一种节能环保型辅助制动装置。但现有的永磁式缓速器所提供的制动力矩大小不能调节，很大程度制约了其应用。本学位论文主要目的是对分级式永磁缓速器结构设计方法进行研究，以期为国内开发具有自主知识产权的永磁式缓速器提供理论方法支持。　　首先，本文研究永磁式缓速器的工作机理、结构、性能特性，分析现有永磁式缓速器应用和发展状况，继而提出分级式永磁缓速器这一新的概念，并分析开发分级式永磁缓速器的必要性。　　其次，建立永磁式缓速器的数学模型，运用解析法推导出气隙磁通密度的表达式，并在此基础上运用源和场理论推导出制动力矩计算公式。并通过台架试验对公式的正确性进行验证，为分级式永磁缓速器的结构设计、参数设计奠定了理论基础。　　然后，根据理论公式，分析各个结构参数对气隙磁场、制动力矩的影响，为分级式永磁缓速器的设计提供了理论依据。通过选择磁极对数、永磁体周向宽度、永磁体轴向长度和气隙大小这四个可以通过机构实现变化的定子参数作为分级式永磁缓速器设计的突破口，提出四类永磁式缓速器制动力矩分级的方法。将现有的国内外研究成果归并到这四类制动力矩分级的方法之下，并补充自己的结构设计，构成完整的分级式永磁缓速器结构设计理论，以填补国内分级式永磁缓速器系统研究的这一研究空白，为分级式永磁缓速器的结构设计提供参考。　　之后，根据上文提出的多种分级式永磁缓速器结构，选择其中基于改变参与制动工作的永磁体周向宽度的鼓式结构方案，以永久磁铁用量最少为目标参数，完成最大制动力矩为800N.m的分级式永磁缓速器结构参数的优化设计。并基于Visual C++，编制出分级式永磁缓速器结构参数优化求解程序，有效地提高了设计效率。　　最后，运用Ansoft Maxwell软件对所设计的分级式永磁缓速器进行三维电磁场仿真分析。通过三维静态分析获得不同制动档位下磁场的分布规律，以及通过三维瞬态电磁场分析获得不同制动档位下涡流密度的分布以及制动力矩-转速特性曲线，由此定性、定量地验证了所设计的分级式永磁缓速器具有期望的制动力矩分级效果。　　收起

... 同一时间,江苏大学何仁教授等^[6]还申请了一种制动力矩可分档的永久磁铁式缓速器专利,它是通过改变磁铁周向转动式永磁缓速器上固定和活动磁极的分布,设计出1/2最大制动力矩的档位 ...

... 1 改变参与工作的磁极对数N_p(结构一)改变实际参与工作的磁极对数N_p,江苏大学何仁教授设计如图9所示的结构^[6] ...

0.0

... 2010年2月北京工业大学李德胜教授等^[7]申请了转子冷却式汽车永磁液冷缓速器发明专利,气缸通过轴承可以推动转子,移动转子可改变永久磁铁与定子之间的相交面积的大小,从而实现永磁式缓速器制动力矩的分级分档或连续调节 ...

... 4 改变参与工作永磁体轴向长度b(结构四)改变参与工作永磁体轴向长度,北京工业大学李德胜教授设计如图12所示的结构^[7] ...

2008

0.0

. 2008, :-

Optimization design research of automobile permanent magnet retarder

汽车永磁缓速器设计理论与试验研究[D]

Ye Le-zhi.

叶乐志

汽车缓速器是一种非摩擦性的辅助制动装置，它在车辆制动之前消耗大部分行驶动能，可以有效提高车辆行驶的安全性和连续制动性能，降低车辆使用成本。上世纪中期许多欧洲国家已颁布交通法规，将缓速器列为汽车的标准配置。近年来，国内随着相关法规的颁布，汽车缓速器也逐步获得应用推广。目前，电涡流缓速器和液力缓速器是国内外应用最广泛的两种产品，但电涡流缓速器制动力矩热衰退严重，体积重量大且耗能高，而液力缓速器价格高，在性价比方面难以满足国内重型货车的要求，致使国内重型货车的缓速器安装率不足1％。因此，研究开发具有自主知识产权的高性价比... 展开汽车缓速器是一种非摩擦性的辅助制动装置，它在车辆制动之前消耗大部分行驶动能，可以有效提高车辆行驶的安全性和连续制动性能，降低车辆使用成本。上世纪中期许多欧洲国家已颁布交通法规，将缓速器列为汽车的标准配置。近年来，国内随着相关法规的颁布，汽车缓速器也逐步获得应用推广。目前，电涡流缓速器和液力缓速器是国内外应用最广泛的两种产品，但电涡流缓速器制动力矩热衰退严重，体积重量大且耗能高，而液力缓速器价格高，在性价比方面难以满足国内重型货车的要求，致使国内重型货车的缓速器安装率不足1％。因此，研究开发具有自主知识产权的高性价比缓速器，对于打破国外缓速器技术垄断，保障行车安全，提高国产汽车的自主创新能力具有重要意义。　　上世纪90年代，日本首次研制成功了一种革命性的永磁缓速器，具有不耗电、重量轻、结构紧凑等优点，但没有得到大规模推广。本文针对永磁缓速器制动力矩小和持续工作能力差等问题，系统研究了永磁缓速器设计的理论和关键技术，提出了一种采用永磁涡流制动原理和水冷散热技术相结合的新型汽车缓速器-水冷式永磁缓速器，并进行了大量的台架和实车试验，形成了水冷式永磁缓速器性能评价体系，取得了许多重要成果。本论文主要章节和内容安排如下：　　第一章绪论部分概述了汽车辅助制动装置作用，安装必要性，国内外法规和应用情况，以及研究意义。介绍了各种汽车缓速器的种类、工作原理、性能比较以及永磁缓速器设计理论和结构的研究进展。通过总结缓速器存在的共性技术问题，提出永磁缓速器的发展方向。综述涡流制动理论和多物理场理论的研究进展，从而提出永磁缓速器设计理论的研究方法。　　第二章提出水冷式永磁缓速器结构及原理。先详细介绍了日本传统永磁缓速器的结构、工作原理、控制方法、安装方法、特点以及使用效果。为克服传统永磁缓速器热衰退严重的问题，提出了一种采用水冷散热的新型永磁缓速器，并介绍了其基本结构和工作原理。该缓速器能够保持较低的工作温度，持续工作时基本不发生制动力矩热衰退，大大提高永磁缓速器的制动性能和持续工作能力。根据整车安装要求，提出了三种适配于重型货车和大型客车的水冷式永磁缓速器结构。研究了水冷式永磁缓速器与整车的电气、散热和制动性能等方面的匹配特性，设计了缓速器电子控制单元和整车冷却系统水管布置方案，并提出了水冷式永磁缓速器制动力矩与车重的匹配关系。　　第三章建立了水冷式永磁缓速器的数学模型。从制动减速度和制动距离两方面评价了缓速器对汽车制动性能的影响，详细分析了新型缓速器单独制动和联合制动时的制动过程。基于电枢反应理论和迭代法求解了缓速器瞬态涡流场，得到了制动力矩和制动功率的解析公式，揭示永磁缓速器制动过程中瞬态电磁场变化规律，建立永磁缓速器的电磁场数学模型。通过分析水冷式缓速器热量传递过程的换热方式、传递路径和边界条件，建立了永磁缓速器温度场的数学模型。分析涡流去磁场和比磁导分布，得到永磁体动态工作点，从而建立永磁体高温失磁的数学模型，提出了分析永磁缓速器中永磁体失磁分析方法。　　第四章建立了永磁缓速器多场耦合模型。建立和数值求解电-磁-热场耦合模型，应用电磁场分析软件得到了磁场和涡流分布图，可视化揭示了永磁缓速器涡流制动的机理。建立和数值求解热.流场耦合模型，应用计算流体力学(CFD)分析软件获得了缓速器定子和永磁体温度场分布图，可视化揭示了定子水道内液体冷却规律。采用半拉格朗日运动坐标系方法建立永磁缓速器的电-磁-热-流场耦合模型，通过试验表明，多场耦合计算结果比单场分析结果更接近试验值。　　第五章研究了永磁缓速器设计的关键技术。通过搭建涡流制动实验平台，发现缓速器低速区制动力矩与吸力近似呈线性的规律，提出一种静态吸力设计方法。利用数值模拟方法求解了缓速器定子材料的电导率、磁导率、铜或铝材料以及镀覆层对制动力矩的影响，并得到了制动力矩与气隙长度、定子厚度、永磁体形状、屏蔽

... 北京工业大学叶乐志在其学位论文中提出了独立磁头的方法^[8],即每块永久磁铁由独立的气缸活塞机构控制,可以独立地变化工作状态,其结构与电涡流缓速器相似,通过控制参与制动工作的磁头对数改变制动力矩的大小 ...

1999

0.0

... 日本冈山大学的Muramatsu等^[9]运用移动坐标系对永磁缓速器进行了3D直流稳态涡流分析 ...

1998

0.0

... Natsumeda等^[10]将有限元同Rosenbrock#cod#x02019 ...

2005

0.0

... 值得一提的是美国德克萨斯州农工大学的Gay等^[11,12]设计了一种摩擦制动器和永磁缓速器联合制动方案,并对联合制动器应用于传统汽车和混合动力汽车上的效果和影响进行了分析 ...

2005

0.0

2006

0.0

. 2006, 6(4):62-65 DOI:doi:10.3321/j.issn:1671-1637.2006.04.014

Braking torque computation method of permanent magnet retarder

车用永磁式缓速器制动力矩的计算方法

He Ren , Zhao Wan-zhong , Niu Run-xin.

何仁, 赵万忠, 牛润新

为了优化永磁式缓速器的结构参数和提高永磁式缓速器的制动性能,应用复矢量磁位方法,分析了缓速器内部的磁位分布,计算了转子鼓中的涡流损耗,推导了永磁式缓速器的制动力矩计算公式,以反映永磁式缓速器制动力矩与各设计参数之间的相互关系.复矢量计算方法的计算结果与缓速器台架试验结果比较和分析表明,试验值与理论值吻合较好,最大误差不大于6%,采用复矢量磁位计算方法计算永磁式缓速器制动力矩具有很好的逼近效果.

... 1 永磁式缓速器的工作原理永磁式缓速器的基本工作原理是:利用电磁原理把汽车行驶的动能转化为热能而散发掉,从而实现汽车的减速和制动^[13] ...

2003

0.0

... 2 气隙磁场的分析计算在对气隙磁场进行分析时,可供选择的方法有解析法^[14,15]和有限元法^[16] ...

1995

0.0

... 2 气隙磁场的分析计算在对气隙磁场进行分析时,可供选择的方法有解析法^[14,15]和有限元法^[16] ...

2010

0.0

... 2 气隙磁场的分析计算在对气隙磁场进行分析时,可供选择的方法有解析法^[14,15]和有限元法^[16] ...

0.0

. , 2004(2):197-200 DOI:doi:10.3321/j.issn:1000-680X.2004.02.020

电涡流缓速器制动力矩的计算方法

He Ren , Yi Feng-yan , He Jian-qing.

何仁, 衣丰艳, 何建清

运用电磁场理论推导了电涡流缓速器的电流密度和制动力矩计算公式,这些计算公式反映了电涡流缓速器各设计参数的相互关系,可用于指导电涡流缓速器的产品开发.

... 计算模型如图4所示^[17],L为以转子毂内径r₂为半径的等效周长,L=2#cod#x003c0 ...

2009

0.0

. 2009, 40(10):18-23

Sensitivity analysis on influence factors for braking performance of permanent magnet type eddy current retarder with uniform design

永磁式涡流缓速器制动性能影响因素敏感性分析

Zhao Xiao-bo , Ji Chang-ying , Zhao Guo-zhu.

赵小波, 姬长英, 赵国柱

摘　要：在分析永磁式涡流缓速器制动力矩与结构参数关系的基础上,将均匀设计和回归分析方法引入到永磁式涡流缓速器制动性能影响因素敏感性分析中。以某型号的永磁式涡流缓速器为例,建立了制动力矩随转子鼓内半径、永磁体周向长度、气隙宽度、转子鼓轴向宽度和永磁体高度5个结构参数变化的回归模型,重点讨论了结构参数间交互作用以及各结构参数对制动力矩的影响程度,基于均匀试验设计和制动性能敏感性分析的结果,采用全排列法对结构参数进行了优化。