基于向量误差修正模型的短时交通参数预测

引用本文

邴其春, 杨兆升, 周熙阳, 马明辉. 基于向量误差修正模型的短时交通参数预测. 2015, 45(4): 1076-1081
BING Qi-chun, YANG Zhao-sheng, ZHOU Xi-yang, MA Ming-hui. Short-term traffic parameters prediction method based on vector error correction model. Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1076-1081 复制到剪切板

Permissions

基于向量误差修正模型的短时交通参数预测

邴其春¹, 杨兆升^1,^2,³, 周熙阳¹, 马明辉¹

1.吉林大学交通学院,长春 130022

2.吉林大学汽车仿真与控制国家重点实验室,长春 130022

3.吉林大学吉林省道路交通重点实验室,长春 130022

杨兆升(1938-),男,教授,博士生导师.研究方向:智能交通系统理论与技术.E-mail:yangzs@jlu.edu.cn

作者简介:邴其春(1989-),男,博士研究生.研究方向:智能交通系统理论与技术.E-mail:bingqc13@mails.jlu.edu.cn

基金:“十二五”国家科技支撑计划项目(2014BAG03B03); “863”国家高技术研究发展计划项目(2012AA112307); 山东省省管企业科技创新项目(20122150251-1)

摘要

为了进一步提高短时交通参数预测的精度,针对交通参数之间存在的内在相关性,在对各交通参数时间序列进行平稳性检验、协整检验的基础上,构建了一种适应于短时交通参数预测的多变量时间序列模型-向量误差修正模型,并对模型的稳定性进行了检验。最后,利用上海市南北高架快速路的感应线圈实测数据进行了实验验证和对比分析。实验结果表明,所构建的向量误差修正模型具有较好的预测效果,能够进一步降低短时交通参数预测的误差。

关键词: 交通运输系统工程; 向量误差修正模型; 交通参数; 短时预测

中图分类号:U491.1 文献标志码:A 文章编号:1671-5497(2015)04-1076-06

Short-term traffic parameters prediction method based on vector error correction model

BING Qi-chun¹, YANG Zhao-sheng^1,^2,³, ZHOU Xi-yang¹, MA Ming-hui¹

1.College of Transportation, Jilin University, Changchun 130022, China

2.State Key Laboratory of Automobile Simulation and Control, Jilin University, Changchun 130022, China

3.Jilin Province Key Laboratory of Road Traffic, Jilin University, Changchun 130022, China

Abstract

In order to further improve the prediction accuracy of short-term traffic parameters, according to the inherent correlation between traffic parameters, on the basis of stationarity test and cointegration test for traffic parameters time series, a multivariate time series model for short-term traffic parameters forecasting is proposed, which is called vector error correction model. The stationarity of the vector error correction model was tested. Validation and comparative analysis were carried out using inductive loop data measured from the north-south viaduct in Shanghai, China. The experiment results indicate that the proposed vector error correction model has good prediction performance and can further reduce the prediction errors of short-term traffic parameters.

Keyword: engineering of communication and transportation system; vector error correction model; traffic parameters; short-term prediction

Show Figures

0 引言

准确、可靠的短时交通参数预测信息是智能交通系统(Intelligent transportation systems, ITS)的基础和关键, 其预测精度直接影响着自适应交通控制系统以及动态交通诱导系统等多项ITS核心功能的应用效果。随着智能交通系统的发展, 短时交通参数预测发挥着越来越重要的作用。传统的预测方法将交通参数数据作为一维时间序列进行预测, 如时间序列模型^[1]、支持向量机模型^[2]、最近邻模型^[3]、神经网络模型^{[4, 5]}等, 此类方法仅考虑了交通参数的时间相关性, 预测效果受到限制。随着研究的深入, 交通参数的时空相关性被应用于短时预测领域。如常刚等^[6]提出了一种基于时空依赖性的区域路网短时交通流预测模型; 高为等^[7]提出一种基于交通流时空变化特性和RBF神经网络的短时交通流预测方法; Mina等^[8]通过构建多变量的时空自回归模型实现了流量和速度的短时多步预测; Stathopoulos等^[9]以预测点的上游检测器数据为基础建立了多变量状态空间模型。上述短时交通参数预测方法大多是以单个交通流参数为基础, 考虑其时间或空间相关性建立预测模型, 忽视了交通参数(流量、速度、占有率)之间内在相关性的有效利用。

本文针对交通参数之间存在的内在相关性, 在深入分析各参数时间序列内在关系的基础上, 引入计量经济学中经典的向量误差修正模型, 构建适应于短时交通参数预测的向量误差修正模型, 并利用上海市南北高架快速路的实测数据进行实验验证。

1 向量误差修正模型

向量误差修正(Vector error correction, VEC)模型是一种具有特定形式的计量经济学模型。其基本思想是:若变量间存在协整关系, 则表明这些变量间存在长期均衡关系, 而这种长期均衡关系是在短期波动过程的不断调整下得以实现的^[10]。交通参数时间序列的一阶差分是平稳序列, 受到各参数之间长期均衡关系的影响, 各参数之间存在一种误差修正机制, 使它们的某些线性组合也是平稳序列, 以避免长期均衡关系出现较大偏差。任何一组相互之间存在协整关系的时间序列都存在误差修正机制, 通过变量之间短期的调节行为, 保持其长期均衡关系。因此, 本文通过深入分析交通参数之间的内在相关性, 试图寻找短时交通参数之间误差修正机制, 构建适应于短时交通参数的向量误差模型。

向量误差修正模型是一种将协整关系和误差修正模型结合起来的多变量时间序列模型, 它是在向量自回归模型的基础上建立起来的。

设y_t=(y₁_t, y₂_t, …, y_kt)为k维随机时间序列, 其中, t=1, 2, …, T, 且y_t~I(1), 即每一个y_it~I(1), i=1, 2, …, k, 如果y_t不受d维外生时间序列x_t=(x₁_t, x₂_t, …, x_dt)影响, 可建立VAR模型为:

$\begin{matrix} \begin{matrix} y_{t} = A_{1} y_{t - 1} + A_{2} y_{t - 2} + \dots + A_{p} y_{t - p} + u_{t} (1) \\ t = 1, 2, \dots, T \end{matrix} \end{matrix}$

式中:y_t为k维模型变量; y_t-p为变量的p阶滞后量; p为滞后阶数; A_p为k× k阶系数矩阵; u_t为随机扰动项。

对式(1)进行差分处理, 可得:

$\begin{matrix} Δ y_{t} = Π y_{t - 1} + \overset{p - 1}{\sum_{i = 1}} Γ_{i} Δ y_{t - i} + u_{i} (2) \end{matrix}$

式中:Π = $\begin{matrix} \overset{p}{\sum_{i = 1}} \end{matrix}$ A_i-I; Γ _i=- $\begin{matrix} \overset{p}{\sum_{j = i + 1}} \end{matrix}$ A_j。

若y_t存在协整关系, 则Π y_t-₁~I $\begin{matrix} (0) \end{matrix}$ , 则式(2)可写成:

$\begin{matrix} Δ y_{t} = αβ' y_{t - 1} + \overset{p - 1}{\sum_{i = 1}} Γ_{i} Δ y_{t - i} + u_{i} (3) \end{matrix}$

式中:β 'y_t-₁=ecm_i-₁为误差修正项, 反映变量之间的长期均衡关系。

式(3)可写成:

$\begin{matrix} Δ y_{t} = αec m_{t - 1} + \overset{p - 1}{\sum_{i = 1}} Γ_{i} Δ y_{t - i} + u_{i} (4) \end{matrix}$

式(4)即为向量误差修正模型, 其中的每一个方程都是一个误差修正模型。

2 数据来源

实验数据来源于上海市南北高架长约10 km快速路上感应线圈检测器采集到的交通流数据, 包括交通流量、地点速度和时间占有率数据。该路段设置有24个主线检测截面和30个匝道检测截面, 分别安装有88个主线检测器和60个匝道检测器。实验数据为2008年9月到10月间连续5个周一的24 h感应线圈数据, 数据采样间隔为20 s。由于20 s采样间隔的交通流数据波动性较大, 较少应用于短时交通参数预测, 本文将其合成为5 min数据进行预测分析。图1为上海市南北高架某路段结构示意图。

	Figure Option View Download New Window
	图1 上海市南北高架某路段结构示意图Fig.1 Road segment of north-south viaduct bridge in Shanghai

3 模型构建

3.1 交通参数时间序列平稳性检验

交通参数时间序列平稳性检验是模型构建的基础, 可以有效避免伪回归现象的出现。本文采用ADF单位根检验法对交通参数时间序列进行平稳性检验。检验结果如表1所示。检验结果表明, 流量、速度、时间占有率三个交通参数的原始时间序列是非平稳的, 而它们的一阶差分是平稳序列, 即交通参数时间序列均为一阶单整, 符合构建VEC模型的前提条件。

表1 ADF单位根检验结果 Table 1 Test results of ADF unit root

3.2 滞后阶数确定

在选取滞后阶数时, 既要满足足够数目的滞后项, 使其能完整反映模型的动态特征, 又要使模型有足够的自由度, 因为随着滞后阶数的增大, 模型的自由度减小^[11]。因此, 本文综合考虑LR、FPE、AIC、SC、HQ五个检验统计量, 通过确定无约束VAR模型的最佳滞后阶数, 进而选取VEC模型的最佳滞后阶数。检验结果如表2所示。

表2 最佳滞后阶数确定 Table 2 Optimal lag order determination

由表2的检验结果可见, 根据LR、FPE、AIC、SC、HQ五个检验统计量确定的无约束VAR模型最佳滞后阶数为3, 而VEC模型的最佳滞后阶数为一阶差分后的滞后阶数, 即为无约束VAR模型的最佳滞后阶数减1, 因此VEC模型的最佳滞后阶数取为2。

3.3 协整检验

向量误差修正模型是具有约束的向量自回归模型, 在建模之前需对交通参数进行协整检验, 只有交通参数之间存在协整关系才能构建向量误差修正模型。由稳定性检验结果可知, 交通参数时间序列均为一阶单整, 因此, 可直接对交通参数数据进行协整检验。本文采用Johansen检验方法进行协整检验, 该方法不仅能够检验出交通参数之间是否存在协整关系, 而且可以准确获得协整向量的个数。上文中确定的无约束VAR模型的最佳滞后阶数为3, 因此, 协整检验的滞后阶数取为2。协整检验结果如表3所示。

表3 Johansen协整检验结果 Table 3 Results of Johansen cointegration test

由表3检验结果可知, 在5%的显著性水平下, 交通流量、地点速度、时间占有率三参数之间存在一个协整关系, 说明交通参数之间存在长期均衡关系, 可以构建VEC模型。将交通参数之间的协整关系标准化得到协整方程为:

O=0.619922S-0.009985V+0.002866 (5)

式中:O表示时间占有率; S表示地点速度; V表示交通流量。

3.4 模型参数估计

由协整检验结果可知, 交通流量、地点速度、时间占有率三参数之间彼此存在协整关系, 在此基础上构建向量误差修正模型, 以考察交通流三参数之间的长期均衡关系。利用EViews7.0软件对VEC模型的参数进行估计, 结果如式(6)~(8)所示。

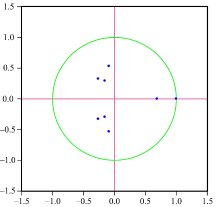
$\begin{matrix} \begin{matrix} ΔV = - 0.000092 (V (- 1) - 84.1374 S (- 1) - \\ 136.2165 O (- 1) + 6478.2725) - \\ 0.3931 ΔV (- 1) - 0.1632 ΔV (- 2) - \\ 0.2146 ΔS (- 1) + 0.0140 ΔS (- 2) + \\ 0.1200 Δ O (- 1) + 0.0517 ΔO (- 2) + 0.080 (6) \\ Δ (S) = 0.0052 (V (- 1) - 84.1374 S (- 1) - \\ 136.2165 O (- 1) + 6478.2725) + \\ 0.0474 ΔV (- 1) - 0.0217 ΔV (- 2) - \\ 0.1937 ΔS (- 1) - 0.0259 ΔS (- 2) - \\ 0.0080 ΔO (- 1) + 0.4439 ΔO (- 2) + 0.0058 (7) \\ Δ (O) = 0.000398 (V (- 1) - 84.1374 S (- 1) - \\ 136.2165 O (- 1) + 6478.2725) - \\ 0.0 234 ΔV (- 1) + 0.0032 ΔV (- 2) - \\ 0.0533 ΔS (- 1) - 0.0347 ΔS (- 2) - \\ 0.2485 ΔO (- 1) - 0.3308 ΔO (- 2) + 0.0092 (8) \end{matrix} \end{matrix}$

3.5 模型稳定性检验

在利用所构建的VEC模型进行短时交通参数预测之前需对模型进行稳定性检验, 如果被估计的VEC模型所有根模的倒数小于1, 即都位于单位圆内, 则该VEC模型是稳定的。VEC模型共有kp个特征根, 其中k为内生变量的个数, p为无约束VAR模型的最佳滞后阶数。如果VEC模型有r个协整关系, 则会有k-r个根等于1。模型稳定性检验结果如图2所示。

	Figure Option View Download New Window
	图2 模型稳定性检验结果Fig.2 Stationarity test results of model

由图2检验结果可见, 所构建的VEC模型有2个根模的倒数在单位圆上(两个点重合), 其余7个均位于单位圆内。因此, 所构建的VEC模型是稳定的, 基于该模型的短时交通参数预测结果是可靠的。

4 预测性能评估

4.1 评价指标

为了评价向量误差修正模型对于短时交通参数的预测效果, 本文引入平均绝对百分比误差(Mean absolute percentage error, MAPE)和均等系数(Equal coefficient, EC)两个评价指标。

平均绝对百分比误差(MAPE):

$\begin{matrix} MAPE = \frac{1}{n} \overset{n}{\sum_{i = 1}} |\frac{y (i) - \hat{y} (i)}{y (i)}| (9) \end{matrix}$

均等系数(EC):

$\begin{matrix} EC = 1 - \frac{\sqrt[]{\overset{n}{\sum_{i = 1}} {(y (i) - \hat{y} (i))}^{2}}}{\sqrt[]{\overset{n}{\sum_{i = 1}} {(y (i))}^{2}} + \sqrt[]{\overset{n}{\sum_{i = 1}} {(\hat{y} (i))}^{2}}} (10) \end{matrix}$

式中: $\begin{matrix} \hat{y} \end{matrix} \begin{matrix} (i) \end{matrix}$ 表示第i时刻的预测值; y $\begin{matrix} (i) \end{matrix}$ 表示第i时刻的真实值; n为样本量。

均等系数表示预测值与实际值之间演化趋势的相似度, 均等系数越大, 说明预测值与实际值之间拟合度越好。

4.2 性能评估

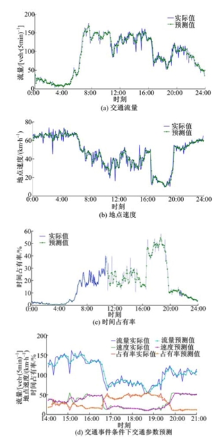
为了验证向量误差修正模型对短时交通参数预测的效果, 本文以东侧主线NBDX16(2)感应线圈检测器采集到的数据为基础, 选取2008年9月1日、9月8日、9月15日和9月22日四天的数据构建向量误差修正模型, 利用9月29日的数据对模型的预测性能进行评估。交通流三参数的预测效果如图3所示。由图3可见, 本文所构建的向量误差修正模型对于交通流量、地点速度和时间占有率三参数均具有较好的预测效果, 预测值与实际值之间拟合效果较好, 预测误差较小。由图3(d)可见, 当发生交通事件时, 交通流量和地点速度急剧下降, 时间占有率急剧升高, 向量误差修正模型能够充分利用交通参数之间的内在相关性, 及时捕获交通参数数据的变化趋势, 在突发交通事件条件下, 向量误差修正模型也具有较高的预测精度。

	Figure Option View Download New Window
	图3 交通参数预测效果图Fig.3 Traffic parameters prediction effect

4.3 对比分析

为对比分析向量误差修正模型在短时交通参数预测方面的优越性, 本文分别选取自回归移动平均模型(Autoregressive integrated moving average model, ARIMA)和文献[6]提出的多变量时间序列状态空间模型作为对比方法, 对实验线路的感应线圈数据进行预测分析。实验结果如表4所示。

表4 预测结果对比分析 Table 4 Analysis of prediction results

由表4可以看出:①不同预测模型对于交通参数的预测效果差别较大, 本文构建的VEC模型充分利用交通参数之间的内在相关性以及长期均衡性, 在MAPE和EC方面均表现最好, 文献[6]方法综合考虑了交通参数的时空相关性, 其预测效果次之, 而ARIMA模型仅考虑了交通参数之间的时间相关性, 预测效果受到限制, 在3种预测方法中预测精度最低; ②同一预测模型对于不同交通参数的预测效果相近, VEC模型对于不同交通参数的预测效果均表现较好, 其MAPE均维持在6%上下, EC在0.96上下, 能够满足短时交通参数预测的需求。综上所述, 本文构建的向量误差修正模型能够较好地适应短时交通参数预测的要求, 进一步降低了短时交通参数预测的误差。

5 结束语

针对交通参数之间存在的内在相关性, 在对各参数时间序列进行平稳性检验、协整检验的基础上, 构建了一种适应于短时交通参数预测的向量误差修正模型, 并以上海市南北高架快速路上感应线圈的实测数据进行了实验验证和对比分析。实验结果表明, 所构建向量误差修正模型的预测效果明显优于对比方法的预测效果, 能够进一步降低短时交通参数预测的误差。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Williams B M. Multivariate vehicular traffic flow prediction: an evaluation of ARIMAX modelingC]∥[The Transportation Research Board Annual Meeting, Washington D C, 2001. [本文引用:1]
[2]	杨兆升, 王媛, 管青. 基于支持向量机方法的短时交通流量预测方法[J]. 吉林大学学报: 工学版, 2006, 36(6): 881-884. Yang Zhao-sheng, Wang Yuan, Guan Qing. Short-time traffic prediction method based on SVM[J]. Journal of Jilin University(Engineering and Technology Edition), 2006, 36(6): 881-884. [本文引用:1]
[3]	周小鹏, 冯奇, 孙立军. 基于最近邻法的短时交通流预测[J]. 同济大学学报: 自然科学版, 2006, 34(10): 1494-1498. Zhou Xiao-peng, Feng Qi, Sun Li-jun. Short-term traffic flow forecasting based on nearest neighbor algorithm[J]. Journal of Tongji University(Nature Science), 2006, 34(10): 1494-1498. [本文引用:1]
[4]	龚勃文, 林赐云, 李静, 等. 基于核自组织映射-前馈神经网络的交通流短时预测[J]. 吉林大学学报: 工学版, 2011, 41(4): 938-942. Gong Bo-wen, Lin Ci-yun, Li Jing, et al. Short-time traffic flow prediction based on KSOM-BP neural network[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(4): 938-942. [本文引用:1]
[5]	樊娜, 赵祥模, 戴明, 等. 短时交通流预测模型[J]. 交通运输工程学报, 2012, 12(4): 114-119. Fan Na, Zhao Xiang-mo, Dai Ming, et al. Short-term traffic flow prediction model[J]. Journal of Traffic and Transportation Engineering, 2012, 12(4): 114-119. [本文引用:1]
[6]	常刚, 张毅, 姚丹亚. 基于时空依赖性的区域路网短时交通流预测模型[J]. 清华大学学报: 自然科学版, 2013, 53(2): 215-221. Chang Gang, Zhang Yi, Yao Dan-ya. Short-time traffic flow forecasting model for regional road network based on spatial-temporal dependency[J]. Journal of Tsinghua University(Science and Technology), 2013, 53(2): 215-221. [本文引用:1]
[7]	高为, 陆百川, 贠天鹂, 等. 基于时空特性和RBF神经网络的短时交通流预测[J]. 交通信息与安全, 2011, 29(1): 16-24. Gao Wei, Lu Bai-chuan, Yun Tian-li, et al. Short-term traffic flow forecasting based on spatiotemporal characteristics of traffic flow and RBF neural network[J]. Journal of Transportation Information and Safety, 2011, 29(1): 16-24. [本文引用:1]
[8]	Mina W, Wynterb L. Real road traffic prediction with spatio-temporal correlation[J]. Transportation Research Part C, 2011, 19(4): 606-616. [本文引用:1]
[9]	Stathopoulos A, Karlaftis M G. A multivariate state space approach for urban traffic flow modeling and prediction[J]. Transportation Research Part C, 2003, 11(2): 121-135. [本文引用:1]
[10]	万莉敏. 我国燃料油期货市场有效性研究[D]. 哈尔滨: 哈尔滨工程大学, 2010. Wan Li-min. The study on efficiency of Chinese fuel oil futures market[D]. Harbin: Harbin Engineering University, 2010. [本文引用:1]
[11]	俞立平, 潘云涛, 武夷山. 工业化与信息化互动关系的实证研究[J]. 中国软科学, 2009(1): 34-40. Yu Li-ping, Pan Yun-tao, Wu Yi-shan. Study on relationship between industrialization and information[J]. China Soft Science Magazine, 2009(1): 34-40. [本文引用:1]

2001

0.0

... 传统的预测方法将交通参数数据作为一维时间序列进行预测,如时间序列模型^[1]、支持向量机模型^[2]、最近邻模型^[3]、神经网络模型^[4,5]等,此类方法仅考虑了交通参数的时间相关性,预测效果受到限制 ...

2006

0.0

. 2006, 36(6):881-884

Short-time traffic prediction method based on SVM

基于支持向量机方法的短时交通流量预测方法

Yang Zhao-sheng , Wang Yuan , Guan Qing.

杨兆升, 王媛, 管青

College of Transportation , Jilin University, Changchun 130022,China

Summarizing the existing prediction models and considering the characteristics of the traffic itself such as nonlinearity, complexity and uncertainty, a shortterm traffic flow prediction model based on support vector machine(SVM) was proposed. The real traffic data validation and the comparison with the traffic flow prediction model based on the BP neural network resulted in a conclusion that this model is superior to the BP neural network model on the aspects of prediction accuracy, convergence time, generalization ability, optimization possibility and so on.

在总结已有多种预测模型的基础上，充分考虑了交通本身所存在的非线性、复杂性和不确定性，提出了一种基于支持向量机的短时交通流量预测模型。实例数据验证结果和基于BP神经网络的预测模型的对比结果表明，该模型在精度、收敛时间、泛化能力、最优性等方面均优于基于BP神经网络的预测模型。

2006

0.0

2011

0.0

. 2011, 41(4):938-942

Short-time traffic flow prediction based on KSOM-BP neural network

基于核自组织映射-前馈神经网络的交通流短时预测

Gong Bo-wen , Lin Ci-yun , Li Jing

龚勃文, 林赐云, 李静

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China|2.College of Transportation, Jilin University, Changchun 130022, China|3.College of Automotive Engineering, Jilin University, Changchun 130022, China

A short-term traffic flow prediction model was built based on KSOM-BP neural network. Using the kernel sample self-organizing map(KSOM) neural network, under the condition without a priori knowledge, the history samples with similar statistic character were classified into several categories by self-organizing and self-learning to enhance the statistic significance of the classified sample. A back-propagation(BP) neural network prediction model was built for the momentum-adaptive learning rate of every category sample to enhance the short-term traffic flow prediction accuracy, reduce the prediction time consumption. The model was validated using the practical road network data. The results show that the statistic index MARE of prediction error of KSOM-BP neural network is less than 7%, and less by 4% than that of BP network based on the whole sample without classification. The modeling time consumption of KSOM-BP neural network is also less than BP neural network without sample classification. All of this proves the validation and state-of-the-art of the proposed method.

提出了一种基于KSOM-BP神经网络的交通流短时预测模型。利用基于核函数的样本自组织映射神经网络(KSOM)，在没有任何先验知识的情况下，自组织、自学习地将具有相似统计特性的历史样本划分成一类，促使分类样本统计特性更集中显著。对每个类别的样本分别建立动量-自适应学习速率的BP神经网络预测模型，以期提高交通流短时预测精度，减少预测时间。结合实际城市道路数据对模型进行验证。验证结果表明：KSOM-BP神经网络的预测误差统计指标MARE小于7%，比基于全部样本训练的BP神经网络的MARE减少4%左右；同时，KSOM-BP神经网络建模时间更短，证明了本文方法的有效性和先进性。

2012

0.0

2013

0.0

... 如常刚等^[6]提出了一种基于时空依赖性的区域路网短时交通流预测模型 ...

2011

0.0

... 高为等^[7]提出一种基于交通流时空变化特性和RBF神经网络的短时交通流预测方法 ...

2011

0.0

... Mina等^[8]通过构建多变量的时空自回归模型实现了流量和速度的短时多步预测 ...

2003

0.0

... Stathopoulos等^[9]以预测点的上游检测器数据为基础建立了多变量状态空间模型 ...

2010

0.0

. 2010, :- DOI:doi:10.7666/d.y1808775

The study on efficiency of Chinese fuel oil futures market[D].

我国燃料油期货市场有效性研究[D]

Wan Li-min.

万莉敏

石油金融发展已成为现阶段我国市场经济改革的核心,石油期货市场作为一个有效的套期保值、参与定价的平台,在短短几十年内已在发达国家得到验证,其发展对于我国石油产业的可持续发展和保证我国石油安全具有重要的现实意义。　　 2004年8月25日,我国推出上海燃料油期货,为我国目前石油期货市场上的唯一品种,本文将对我国燃料油期货市场的发展和运行进行深入的研究,以我国燃料油期货推出以来的市场表现为依据,选择上海燃料油期货价格采用国内外先进的协整分析、误差修正及神经网络等方法,研究我国燃料油期货自上市以来五年多的市场表现,对我国燃... 展开石油金融发展已成为现阶段我国市场经济改革的核心,石油期货市场作为一个有效的套期保值、参与定价的平台,在短短几十年内已在发达国家得到验证,其发展对于我国石油产业的可持续发展和保证我国石油安全具有重要的现实意义。　　 2004年8月25日,我国推出上海燃料油期货,为我国目前石油期货市场上的唯一品种,本文将对我国燃料油期货市场的发展和运行进行深入的研究,以我国燃料油期货推出以来的市场表现为依据,选择上海燃料油期货价格采用国内外先进的协整分析、误差修正及神经网络等方法,研究我国燃料油期货自上市以来五年多的市场表现,对我国燃料油期货市场长期和短期的价格发现功能和避险功能等方面进行深入的实证研究,旨在明确我国燃料油期货市场的市场有效性程度并对其进行分析,发现问题并针对问题症结寻找解决措施,即围绕如何提升我国燃料油期货市场有效性的具体措施提出政策建议,旨在推进我国石油期货市场健康发展,确保我国石油期货市场的套期保值和避险功能得以最大程度的发挥,进而保证我国石油安全。收起

... 其基本思想是:若变量间存在协整关系,则表明这些变量间存在长期均衡关系,而这种长期均衡关系是在短期波动过程的不断调整下得以实现的^[10] ...

0.0

. , 2009(1):34-40 DOI:doi:10.3969/j.issn.1002-9753.2009.01.006

Study on relationship between industrialization and information

Yu Li-ping , Pan Yun-tao , Wu Yi-shan.

俞立平, 潘云涛, 武夷山

本文基于向量自回归模型对工业化与信息化的关系进行了分析.结果表明,信息化是工业化的格兰杰原因,但工业化不是信息化的格兰杰原因.信息化水平与工业化水平存在着长期稳定的动态关系,信息化的发展能够带动工业化的发展.信息化波动是影响工业化波动的主要原因,但工业化的波动不是影响信息化波动的主要原因.工业化对信息化的影响速度要大于信息化对工业化的影响速度,并且工业化对信息化的影响更为稳定.

... 2 滞后阶数确定在选取滞后阶数时,既要满足足够数目的滞后项,使其能完整反映模型的动态特征,又要使模型有足够的自由度,因为随着滞后阶数的增大,模型的自由度减小^[11] ...