协调控制交叉口短车道长度和配时参数协同优化

引用本文

姚荣涵, 彭程, 周红媚. 协调控制交叉口短车道长度和配时参数协同优化. 2015, 45(4): 1082-1087
YAO Rong-han, PENG Cheng, ZHOU Hong-mei. Synergistic optimization of short lane length and signal timing parameters for adjacent intersections with coordinated signals. Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1082-1087 复制到剪切板

Permissions

协调控制交叉口短车道长度和配时参数协同优化

姚荣涵, 彭程, 周红媚

大连理工大学交通运输学院,辽宁大连 116024

周红媚(1981-),女,讲师,博士.研究方向:智能交通系统,交通安全.E-mail:hzhou@dlut.edu.cn

作者简介:姚荣涵(1979-),女,副教授,博士.研究方向:交通流理论,交通控制,交通规划.E-mail:cyanyrh@dlut.edu.cn

基金:国家自然科学基金项目(51308092)

摘要

为了优化配置共有路段上均含左转短车道的相邻协调控制交叉口的时空资源,以最大化交叉口通行能力和最小化车辆总延误为目标,以左转短车道长度和相位有效绿灯时间为决策变量,建立了交叉口周期时长与绿信比组合优化模型。为验证优化模型的有效性,设计了一个案例,使用优化模型和韦伯斯特模型分别获得每个交叉口的配时方案,并使用已有方法计算了相邻交叉口协调相位的绿时差,进而使用VISSIM软件模拟了两种配时方案下的交通流运行状况。结果显示:与韦伯斯特方法相比,本文优化方法能使交叉口车均延误降低约30%,而通过车辆数略有增加。

关键词: 交通运输系统工程; 左转短车道; 协调控制; 通行能力; 车均延误

中图分类号:U491.1 文献标志码:A 文章编号:1671-5497(2015)04-1082-06

Synergistic optimization of short lane length and signal timing parameters for adjacent intersections with coordinated signals

YAO Rong-han, PENG Cheng, ZHOU Hong-mei

School of Transportation and Logistics, Dalian University of Technology, Dalian 116024, China

Abstract

To optimally allocate the time and space resources for two adjacent intersections with coordinated signals and short left-turn lanes on the common section of a road, an optimization model was presented to jointly obtain the signal cycle length and green slit for each intersection. The objectives are to maximize the passing capacity of the entire intersection and minimize the total delay of vehicles. The decision variables of the model are the length of each short left-turn lane and the effective green time per phase. A case was designed to verify the effectiveness of the proposed model. First, two signal timing plans for each intersection were obtained using the proposed model and Webster model, respectively. Then, the offset between coordinated phases was calculated by a known method. Finally, the traffic operations under the two signal timing scenarios were simulated using VISSIM software. The outcomes show that the unit delay is decreased by 30% and the vehicle throughput is slightly increased for each intersection under the optimization scenario.

Keyword: engineering of communications and transportation system; short left-turn lanes; coordinated signals; capacity; unit delay

Show Figures

0 引言

为提高交叉口通行能力, 进口道常常被展宽以便增加车道, 新增加的车道往往由于空间限制而形成短车道。短车道对进口道饱和流率、交叉口通行能力、车辆延误等具有重要影响。近年来, 国内外诸多学者在相关方面的研究成果主要集中于两方面:①短车道对交叉口通行能力的影响。针对含共用车道和左转短车道的信号交叉口, Wu等^[1]提出一种估计整个进口道通行能力的方法。针对不同的左转信号设计方案, Zhang等^[2]使用概率论建立了左转展宽车道及其邻近的直行车道的通行能力计算模型, 并使用CORSIM仿真软件对通行能力模型进行了验证。考虑到短车道存在排队阻塞的情况, 杨晓光等^[3]针对不同信号相位方案建立了车道组通行能力计算模型。针对拥挤交通流条件下左转展宽车道存在排队溢出和车道进口堵塞的情况, Yin等^[4]建立了保护左转通行能力模型和许可左转通行能力模型, 并使用CORSIM仿真软件对所提出的模型进行了验证; ②短车道长度的确定。Kikuchi等^{[5, 6]}针对双左转短车道和一条车道在交叉口处分为3条车道的情况分别提出短车道长度确定方法。Qi等^[7]认为左转短车道长度由排队存储长度和减速长度两部分组成, 并使用HCS+和Synchro两种分析模型以及SimTraffic和VISSIM两种仿真模型分别提出排队存储长度估计模型和减速长度估计模型。从上述研究可以看出, 左转短车道的设置对交叉口交通流的运行具有重要影响。课题组曾针对共有路段上均含左转短车道的情况建立了相邻交叉口短车道长度与配时参数的协同优化模型, 不过只考虑了非协调信号控制的情形^{[8, 9]}。在此基础上, 本文针对相邻协调控制交叉口探讨短车道长度与配时参数的协同优化问题。

1 模型建立

韦伯斯特-柯布理论是一种经典的信号配时设计方法。对于单点信号配时设计, 该理论以交叉口所有车辆总延误最小为目标获得最佳周期时长, 然后按等饱和度原则为各相位分配有效绿灯时间^[10]。对于协调信号配时设计, 该理论首先按单点信号配时方法计算各个交叉口的最佳周期时长; 然后, 将其中的最大值作为所有交叉口的共用周期时长; 最后, 按等饱和度原则, 根据共用周期时长为每个交叉口的每个相位分配有效绿灯时间。显然, 韦伯斯特-柯布理论无法考虑短车道的存在对交叉口通行能力、延误等造成的影响, 也不能优化短车道长度。鉴于此, 本文建立相邻协调控制交叉口短车道长度与配时参数的协同优化模型。

1.1 优化目标

根据已有研究^{[8, 9]}, 为了优化配置协调信号控制交叉口的时空资源, 应以最大化交叉口通行能力和最小化车辆延误为优化目标。

这里考虑固定式协调控制方式, 且不考虑存在搭接相位的情况, 则交叉口通行能力可表达为:

$\begin{matrix} Q^{η} = \{\begin{matrix} \frac{1}{C^{η}} \overset{n^{η}}{\sum_{i = 1}} \overset{m_{i}^{η}}{\sum_{j = 1}} (S_{fij}^{η} g_{i}^{η} + δ_{ij}^{η} S_{sij}^{η} g_{ij}^{η}); \\ g_{i}^{η} \geq g_{ij}^{η}, η \in \{a, b\} \\ \frac{1}{C^{η}} \overset{n^{η}}{\sum_{i = 1}} \overset{m_{i}^{η}}{\sum_{j = 1}} (S_{fij}^{η} + δ_{ij}^{η} S_{sij}^{η}) g_{i}^{η}; \\ g_{i}^{η} < g_{ij}^{η}, η \in \{a, b\} \end{matrix} (1) \end{matrix}$

式中:C^η= $\begin{matrix} \overset{n^{η}}{\sum_{i = 1}} \end{matrix} \begin{matrix} g_{i}^{η} \end{matrix}$ +L^η; $\begin{matrix} g_{ij}^{η} \end{matrix}$ = $\begin{matrix} D_{ij}^{η} \end{matrix}$ t/h; Q^η为交叉口η 的通行能力; C^η为交叉口η 的周期时长; n^η为交叉口η 的相位数; $\begin{matrix} g_{i}^{η} \end{matrix}$ 为交叉口η 第i相位的有效绿灯时间; L^η为交叉口η 的总损失时间; $\begin{matrix} g_{ij}^{η} \end{matrix}$ 为交叉口η 第i相位第j车道组短车道上排队车辆完全释放所需时间; $\begin{matrix} D_{ij}^{η} \end{matrix}$ 为交叉口η 第i相位第j车道组的短车道长度; t为短车道上每辆车驶离交叉口所需时间; h为短车道上每辆车所占空间长度; $\begin{matrix} m_{i}^{η} \end{matrix}$ 为交叉口η 第i相位的车道组数; $\begin{matrix} S_{fij}^{η} \end{matrix}$ 为交叉口η 第i相位第j车道组的完整车道饱和流率; $\begin{matrix} δ_{ij}^{η} \end{matrix}$ 为系数, 当交叉口η 第i相位第j车道组包含短车道时, $\begin{matrix} δ_{ij}^{η} \end{matrix}$ =1; 否则, $\begin{matrix} δ_{ij}^{η} \end{matrix}$ =0; $\begin{matrix} S_{sij}^{η} \end{matrix}$ 为交叉口η 第i相位第j车道组的短车道饱和流率。

根据HCM 2000^[11], 交叉口所有车辆的总延误可表达为:

$\begin{matrix} \begin{matrix} D^{η} = \overset{n^{η}}{\sum_{i = 1}} \overset{m_{i}^{η}}{\sum_{j = 1}} q_{ij}^{η} [d_{1 ij}^{η} (P F_{ij}^{η}) + d_{2 ij}^{η} + d_{3 ij}^{η}] (2) \\ η \in \{a, b\} \end{matrix} \end{matrix}$

式中: $\begin{matrix} d_{1 ij}^{η} \end{matrix}$ =0.5C^η(1- $\begin{matrix} λ_{i}^{η} \end{matrix}$ )²/[1-min(1, $\begin{matrix} x_{ij}^{η} \end{matrix}$ ) $\begin{matrix} λ_{i}^{η} \end{matrix}$ ]; $\begin{matrix} d_{2 ij}^{η} \end{matrix}$ =

900T $\begin{matrix} [(x_{ij}^{η} - 1) + \sqrt[]{{(x_{ij}^{η} - 1)}^{2} + 8 k I_{ij}^{η} x_{ij}^{η} / Q_{ij}^{η}}] \end{matrix}$ ;

$\begin{matrix} Q_{ij}^{η} \end{matrix}$ = $\begin{matrix} \{\begin{matrix} (S_{fij}^{η} g_{i}^{η} + δ_{ij}^{η} S_{sij}^{η} g_{ij}^{η}) / C^{η}; g_{i}^{η} \geq g_{ij}^{η} \\ (S_{fij}^{η} + δ_{ij}^{η} S_{sij}^{η}) g_{i}^{η} / C^{η}; g_{i}^{η} < g_{ij}^{η} \end{matrix} \end{matrix}$ ; $\begin{matrix} λ_{i}^{η} \end{matrix}$ = $\begin{matrix} \frac{g_{i}^{η}}{C^{η}} \end{matrix}$ ;

$\begin{matrix} x_{ij}^{η} \end{matrix}$ = $\begin{matrix} q_{ij}^{η} \end{matrix}$ / $\begin{matrix} Q_{ij}^{η} \end{matrix}$ ; D^η为交叉口η 所有车辆的总延误; $\begin{matrix} d_{1 ij}^{η} \end{matrix}$ 为交叉口η 第i相位第j车道组的均衡相位延误; $\begin{matrix} d_{2 ij}^{η} \end{matrix}$ 为交叉口η 第i相位第j车道组的随机附加延误; $\begin{matrix} d_{3 ij}^{η} \end{matrix}$ 为交叉口η 第i相位第j车道组的初始排队附加延误; $\begin{matrix} Q_{ij}^{η} \end{matrix}$ 为交叉口η 第i相位第j车道组的通行能力; $\begin{matrix} λ_{i}^{η} \end{matrix}$ 为交叉口η 第i相位的绿信比; $\begin{matrix} x_{ij}^{η} \end{matrix}$ 为交叉口η 第i相位第j车道组的饱和度; $\begin{matrix} q_{ij}^{η} \end{matrix}$ 为交叉口η 第i相位第j车道组的流量; P $\begin{matrix} F_{ij}^{η} \end{matrix}$ 为交叉口η 第i相位第j车道组的信号联动修正系数; $\begin{matrix} I_{ij}^{η} \end{matrix}$ 为交叉口η 第i相位第j车道组的上游调节增量延误修正系数; T为分析期持续时间; k为信号控制类型的延误修正系数。

1.2 约束条件

为了充分利用左转短车道, 相位有效绿灯时间应该不小于该相位每条短车道上排队车辆释放完毕所需时间, 即:

$\begin{matrix} g_{i}^{η} \geq g_{ij}^{η}; \forall δ_{ij}^{η} = 1, η \in \{a, b\} (3) \end{matrix}$

每个相位的有效绿灯时间应该不小于一个临界值, 即:

$\begin{matrix} g_{i}^{η} \geq g_{\min}; η \in \{a, b\} (4) \end{matrix}$

式中:g_min为最小有效绿灯时间。

对某一交叉口来讲, 所有相位有效绿灯时间之和加上总损失时间等于信号周期时长, 这一周期时长应该在合理的上、下限之间, 即:

$\begin{matrix} C_{\min} \leq \overset{n^{η}}{\sum_{i = 1}} g_{i}^{η} + L^{η} \leq C_{\max}; η \in \{a, b\} (5) \end{matrix}$

式中:C_min为最小周期时长; C_max为最大周期时长。

受交叉口空间范围限制, 每条短车道的渠化长度不应该超过实际道路的限制长度, 即:

$\begin{matrix} 0 \leq D_{ij}^{η} \leq D_{maxij}^{η}; \forall δ_{ij}^{η} = 1, η \in \{a, b\} (6) \end{matrix}$

式中: $\begin{matrix} D_{maxij}^{η} \end{matrix}$ 为交叉口η 第i相位第j车道组所含短车道的限制长度, 可取路段长度。

共有路段上关联短车道的长度应该满足:

$\begin{matrix} D_{kl}^{a} + D_{mn}^{b} \leq D_{0}; \forall δ_{kl}^{a} = 1, δ_{mn}^{b} = 1 (7) \end{matrix}$

式中: $\begin{matrix} D_{kl}^{a} \end{matrix}$ 为共有路段上交叉口a的短车道长度; $\begin{matrix} D_{mn}^{b} \end{matrix}$ 为共有路段上交叉口b的短车道长度; D₀为共有路段长度。

假设不存在双周期的情况, 那么两个交叉口的信号周期时长应该相等, 即:

$\begin{matrix} \overset{n^{a}}{\sum_{i = 1}} g_{i}^{a} + L^{a} = \overset{n^{b}}{\sum_{i = 1}} g_{i}^{b} + L^{b} (8) \end{matrix}$

1.3 优化模型

如果在满足式(3)~(8)的约束条件下最大化式(1)且最小化式(2), 则可得优化模型为:

$\begin{matrix} \{\begin{matrix} \max Q^{η} = \frac{1}{C^{η}} \overset{n^{η}}{\sum_{i = 1}} \overset{m_{i}^{η}}{\sum_{j = 1}} (S_{fij}^{η} g_{i}^{η} + δ_{ij}^{η} S_{sij}^{η} D_{ij}^{η} t / h) \\ \min D^{η} = \overset{n^{η}}{\sum_{i = 1}} \overset{m_{i}^{η}}{\sum_{j = 1}} q_{ij}^{η} [d_{1 ij}^{η} (P F_{ij}^{η}) + d_{2 ij}^{η} + d_{3 ij}^{η}] \\ s . t . Eqs . (3) ~ (8) \end{matrix} (9) \end{matrix}$

式(9)是一个线性不等式和等式约束条件下的多目标优化问题。根据运筹学, 多目标优化问题通常被转换成单目标优化问题来求解。转换后的最小化问题可以由MATLAB软件提供的fmincon函数来求解。为此, 使用MATLAB软件编制模型求解程序, 所采用的目标函数为:

$\begin{matrix} \min (D^{a} + D^{b}) / (Q^{a} + Q^{b}) \end{matrix}$

1.4 相位差优化

尽管相位差隐含在模型(9)中, 然而优化模型不能直接获得相位差。同样, 韦伯斯特模型也不能直接计算相位差。为了获得协调相位的绿时差, 这里采用文献[12]提供的相位差优化方法来进行计算。该方法假设车流到达率稳定, 根据交通调查确定协调相位绿灯期间驶离停车线的车队所包含的车辆数。然后, 将车队在交叉口的受阻情况分为头车受阻和非头车受阻两种情况, 根据车辆到达-驶离曲线图建立干线车流总延误与协调相位绿时差之间的函数关系。最后, 通过最小化干线车流总延误获得协调相位的最佳绿时差。

2 案例验证

2.1 案例介绍

为验证优化模型(9), 设计如图1所示的两个相邻交叉口, 交叉口a的东进口道与交叉口b的西进口道均渠化5条车道, 由内向外分别为左转、直行、直行、直行和直右, 其他进口道均渠化4条车道, 由内向外分别为左转、直行、直行和直右。假定左转车道饱和流率为1600 pcu/h, 直行车道饱和流率为1800 pcu/h, 直右车道饱和流率为1700 pcu/h^[11]。此外, 交叉口a与b之间的共有路段的长度为300 m, 交叉口a与b的东进口道与西进口道的停车线之间的距离均为341.5 m。

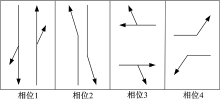
	Figure Option View Download New Window
	图1 交叉口a、b的渠化方案Fig.1 Channelization schemes for intersections a and b

假设交叉口a与b均采用如图2所示的四相位信号控制方案, 东西向直行相位为协调相位, 协调相位控制车流在干道上的平均行驶速度为12 m/s。对于由交叉口a向b和相反方向的干线车流, 假定协调相位绿灯期间驶离停车线的车队所包含的车辆数分别为17 pcu和18 pcu。

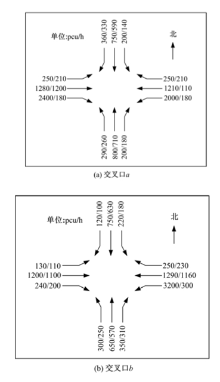
	Figure Option View Download New Window
	图2 交叉口a、b的信号相位方案Fig.2 Signal phase plans for intersections a and b

图3为交叉口a与b各进口道各流向车流的交通量, 斜线前数字为高峰小时内车道组的最高15 min流率, 斜线后数字为车道组的小时流量。

	Figure Option View Download New Window
	图3 各股车流的最高15 min流率与小时流量Fig.3 Peak 15 min flow rate and hourly volume for each movement

2.2 参数取值

协调相位的信号联动修正系数为^[11]:

$\begin{matrix} P F_{ij}^{η} = \frac{(1 - R_{p} g_{i}^{η} / C) f_{PA}}{1 - g_{i}^{η} / C} (10) \end{matrix}$

式中:R_p为车队系数; f_PA为绿灯期间车辆成队列到达的修正系数。

当估计未来的协调信号配时方案时, 对于协调相位控制的直行车流或直左车流, 其到达类型假设为4, 此时R_p=1.333, f_PA=1.15; 对于非协调相位控制的车流或有专用相位的左转车流, 其到达类型假设为3, 此时R_p=1, f_PA=1。

对于不受上游交叉口影响的车流, 其上游调节增量延误修正系数 $\begin{matrix} I_{ij}^{η} \end{matrix}$ =1。对于受上游交叉口影响的车流, 其上游调节增量延误修正系数为^[11]:

$\begin{matrix} I_{ij}^{η} = 1 - 0.91 X_{u}^{2.68} (11) \end{matrix}$

式中:X_u为对该股车流有贡献的所有上游车流按流量进行加权所得的饱和度。

参考相关文献^{[11, 13]}, 这里分析期持续时间T=1 h, k=0.5, 相位损失时间l=3 s, 最小周期时长C_min=40 s, 最大周期时长C_max=180 s。此外, 假定初始时刻无滞留排队, 则 $\begin{matrix} d_{3 ij}^{η} \end{matrix}$ =0 s。

2.3 优化结果分析

针对上述案例, 表1列出了由优化模型和韦伯斯特模型分别得到的优化结果。由表1可知, 与韦伯斯特模型相比, 优化模型能够优化短车道长度, 虽然使交叉口通行能力略有下降、饱和度略有提高, 但使共用周期时长明显缩短、车均延误明显降低。

在表1所示的单点信号配时参数的基础上, 用已有相位差优化方法可得交叉口b相对于交叉口a的协调相位的绿时差分别为51 s和78 s^[12]。

表1 不同模型的优化结果 Table 1 Optimization outcomes from different models

2.4 仿真试验

如前所述, 使用优化模型计算出短车道长度和配时参数, 根据相位差优化方法计算出协调相位的绿时差, 并结合配时参数形成优化方案。使用韦伯斯特模型计算出配时参数, 同样根据相位差优化方法计算出协调相位的绿时差, 并结合配时参数形成韦伯斯特方案。

这里按以下步骤进行仿真试验:

(1)采用优化模型所得的短车道长度, 使用交通仿真软件VISSIM建立除信号配时方案以外的交通流仿真模型。

(2)根据协调相位的绿时差针对优化方案和韦伯斯特方案分别计算信号控制器之间的相位差, 并在VISSIM软件中设置相应的信号配时方案。

(3)分别采用两种信号配时方案运行交通流仿真模型, 并获得相应的仿真结果。

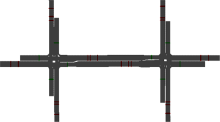
在仿真过程中, 采用多步运行模式, 设仿真次数和仿真时间分别为20 s和3600 s。为了评价交通流运行状况, 设置如图4所示的行程时间检测区段, 各检测区段长度均为150 m, 并选取车均延误、平均停车次数和通过车辆数三种性能指标。表2列出了优化方案和韦伯斯特方案下各交叉口以及两个交叉口整体的三种性能指标。

由表2可以看出, 对每个交叉口来讲, 除交叉口b的平均停车次数外, 本文优化方案的所有性能指标均好于韦伯斯特方案。对两个交叉口整体来讲, 与韦伯斯特方案相比, 优化方案使车均延误降低了17.95 s, 平均停车次数减少0.02, 通过车辆数增加36 pcu/h。总的来说, 优化方案好于韦伯斯特方案。由于优化方案使车均延误明显降低, 因此, 优化方案能够有效提高交叉口的服务水平。

	Figure Option View Download New Window
	图4 行程时间检测区段设置Fig.4 Settings of travel time sections

表2 不同方案的仿真结果 Table 2 Simulation outcomes under different scenarios

3 结束语

针对共有路段均含左转短车道的相邻协调控制交叉口, 建立以交叉口通行能力最大和车辆总延误最小为目标函数的优化模型。由于优化模型不能直接获得相位差, 采用已有方法计算相位差。为了验证优化模型的有效性, 设计了一个案例, 并采用韦伯斯特模型作对比。对比分析了优化模型和韦伯斯特模型计算的信号配时参数与交叉口性能指标。借助相位差优化方法获得了信号配时的优化方案和韦伯斯特方案。使用交通仿真软件VISSIM模拟了这两种配时方案下交通流的运行状况。结果显示, 与韦伯斯特方案相比, 优化方案使车均延误明显降低, 交叉口服务水平有所提升。此外, 优化方案尽管使交叉口通行能力略有下降, 但是交叉口通过车辆数略有增加。研究成果表明, 本文提出的优化模型和方法能够最佳地配置共有路段均含左转短车道的相邻协调控制交叉口的时空资源, 为建立交叉口群时空资源优化模型奠定基础, 为解决城市交通拥堵问题提供理论依据与参考, 具有重要的科学意义与应用价值。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Wu Ning. Total approach capacity at signalized intersections with shared and short lanes: generalized model based on a simulation study[C]∥Transportation Research Record, 2007, 2027: 19-26. [本文引用:1]
[2]	Zhang Yun-long, Tong Jia-xin. Modeling left-turn blockage and capacity at signalized intersection with short left-turn bay[C]∥Transportation Research Record, 2008, 2017: 71-76. [本文引用:1]
[3]	杨晓光, 赵靖, 曾滢, 等. 短车道对信号交叉口通行能力影响研究[J]. 公路交通科技, 2008, 25(12): 151-156. Yang Xiao-guang, Zhao Jing, Zeng Ying, et al. Research on impact of short lane on signalized intersection capacity[J]. Journal of Highway and Transportation Research and Development, 2008, 25(12): 151-156. [本文引用:1]
[4]	Yin Kai, Zhang Yun-long, Wang X Bruce. Analytical models for protected plus permitted left-turn capacity at signalized intersection with heavy traffic[C]∥Transportation Research Record, 2010, 2192: 177-184. [本文引用:1]
[5]	Kikuchi S, Kii M, Chakroborty P. Lengths of double or dual left-turn lanes[C]∥Transportation Research Record, 2004, 1881: 72-78. [本文引用:1]
[6]	Kikuchi S, Kronprasert N, Kii M. Lengths of turn lanes on intersection approaches: three-branch fork lanes-left-turn, through, and right-turn Lanes[C]∥Transportation Research Record, 2007, 2023: 92-101. [本文引用:1]
[7]	Qi Yi Grace, Guo Lei, Yu Lei, et al. Estimation of design lengths of left-turn lanes[J]. Journal of Transportation Engineering, 2012, 138(3): 274-283. [本文引用:1]
[8]	姚荣涵, 王建丽, 贾婧. 相邻交叉口短车道长度与配时参数协同优化[J]. 大连理工大学学报, 2012, 52(4): 546-552. Yao Rong-han, Wang Jian-li, Jia Jing. Synergistic optimization of short lane length and signal timing parameters for two adjacent intersections[J]. Journal of Dalian University of Technology, 2012, 52(4): 546-552. [本文引用:2]
[9]	Yao Rong-han. Sensitivity analysis of optimiza- tion models for two adjacent intersections with correlated short left-turn lanes[J]. Transport, 2013, 28(3): 256-269. [本文引用:2]
[10]	全永燊. 城市交通控制[M]. 北京: 人民交通出版社, 1989: 95-103. [本文引用:1]
[11]	Transportation Research Board. Highway capacity manual (HCM) 2000[R]. Washington D C: National Research Council, 2001. [本文引用:5]
[12]	卢凯, 徐建闽. 干道协调控制相位差模型及其优化方法[J]. 中国公路学报, 2008, 21(1): 83-88. Lu Kai, Xu Jian-min. Offset model for arterial road coordinate control and its optimization method[J]. China Journal of Highway and Transport, 2008, 21(1): 83-88. [本文引用:1]
[13]	吴兵, 李晔. 交通管理与控制[M]. 北京: 人民交通出版社, 2009: 160-165. [本文引用:1]

2007

0.0

... 针对含共用车道和左转短车道的信号交叉口,Wu等^[1]提出一种估计整个进口道通行能力的方法 ...

2008

0.0

... 针对不同的左转信号设计方案,Zhang等^[2]使用概率论建立了左转展宽车道及其邻近的直行车道的通行能力计算模型,并使用CORSIM仿真软件对通行能力模型进行了验证 ...

2008

0.0

. 2008, 25(12):151-156 DOI:doi:10.3969/j.issn.1002-0268.2008.12.029

Research on impact of short lane on signalized intersection capacity

短车道对信号交叉口通行能力影响研究

Yang Xiao-guang , Zhao Jing , Zeng Ying

杨晓光, 赵靖, 曾滢

Since the limited length of short lane,there occurs the potential effect of queue blockage for the road widening intersections.Based on the related results of traffic flow theory and probability theory,the impact of the short lane on the capacity of the signalized intersections was worked out with the qualitative and quantitative analysis.For the three different signal-phase programs,the calculation model of lane group's capacity was established with the consideration of potential blockage and tested with simulation method.Then,the study on the related factors and the sensitivity analysis about the impact on the capacity due to the short lane were conducted.According to the study,the length of short lane and the signal phase effect the signalized intersection capacity greatly,and there exists an optimum signal cycle to the capacity.

针对交叉口进口道拓宽后形成的短车道,由于其长度的限制,存在因车辆排队溢出而造成阻塞的问题,结合交通流理论和概率论的相关成果,从定性分析和定量计算两方面研究了短车道排队阻塞对信号交叉口通行能力的影响。针对3种不同的信号相位方案,建立了考虑短车道潜在排队阻塞情况下的车道组通行能力计算模型,并通过仿真对模型进行了检验。在此基础上,进行了短车道条件下相关因素对信号交叉口通行能力影响的敏感性分析。研究发现在交叉口进口道存有短车道条件下,短车道长度、信号相位方案对通行能力起主要影响;同时对通行能力而言,存在最佳信号周期。

... 考虑到短车道存在排队阻塞的情况,杨晓光等^[3]针对不同信号相位方案建立了车道组通行能力计算模型 ...

2010

0.0

... 针对拥挤交通流条件下左转展宽车道存在排队溢出和车道进口堵塞的情况,Yin等^[4]建立了保护左转通行能力模型和许可左转通行能力模型,并使用CORSIM仿真软件对所提出的模型进行了验证 ...

2004

0.0

... Kikuchi等^[5,6]针对双左转短车道和一条车道在交叉口处分为3条车道的情况分别提出短车道长度确定方法 ...

2007

0.0

... Kikuchi等^[5,6]针对双左转短车道和一条车道在交叉口处分为3条车道的情况分别提出短车道长度确定方法 ...

2012

0.0

... Qi等^[7]认为左转短车道长度由排队存储长度和减速长度两部分组成,并使用HCS+和Synchro两种分析模型以及SimTraffic和VISSIM两种仿真模型分别提出排队存储长度估计模型和减速长度估计模型 ...

2012

0.0

. 2012, 52(4):546-552

Synergistic optimization of short lane length and signal timing parameters for two adjacent intersections

相邻交叉口短车道长度与配时参数协同优化

Yao Rong-han , Wang Jian-li , Jia Jing.

姚荣涵, 王建丽, 贾婧

针对相邻交叉口在共有连线上均渠化左转短车道的现况,研究其时空资源的最优配置.通过分析短车道对进口道饱和流率的影响,建立以交叉口通行能力最大化与车均延误最小化为目标函数、以短车道长度和相位有效绿灯时间为决策变量的多目标优化模型.以大连市两相邻交叉口为例,通过Matlab软件对优化模型进行编程求解,进而利用VISSIM 软件对现有方案和优化方案分别进行仿真试验.结果显示,优化方案虽然使每个交叉口通行能力减小,但是也使每个交叉口车均延误、饱和度和平均排队长度减少. 此外,优化方案使每个交叉口通行能力与车均延误之比增大,使单位时间内通过两个交叉口的总车辆数增加.研究成果表明,交通组织与信号控制的协同优化设计可以实现交叉口群的时空资源的最优配置.

... 课题组曾针对共有路段上均含左转短车道的情况建立了相邻交叉口短车道长度与配时参数的协同优化模型,不过只考虑了非协调信号控制的情形^[8,9] ...

... 1 优化目标根据已有研究^[8,9],为了优化配置协调信号控制交叉口的时空资源,应以最大化交叉口通行能力和最小化车辆延误为优化目标 ...

2013

0.0

... 课题组曾针对共有路段上均含左转短车道的情况建立了相邻交叉口短车道长度与配时参数的协同优化模型,不过只考虑了非协调信号控制的情形^[8,9] ...

... 1 优化目标根据已有研究^[8,9],为了优化配置协调信号控制交叉口的时空资源,应以最大化交叉口通行能力和最小化车辆延误为优化目标 ...

1989

0.0

... 对于单点信号配时设计,该理论以交叉口所有车辆总延误最小为目标获得最佳周期时长,然后按等饱和度原则为各相位分配有效绿灯时间^[10] ...

2001

0.0

... 根据HCM 2000^[11],交叉口所有车辆的总延误可表达为: ...

... 假定左转车道饱和流率为1600 pcu/h,直行车道饱和流率为1800 pcu/h,直右车道饱和流率为1700 pcu/h^[11] ...

... 2 参数取值协调相位的信号联动修正系数为^[11]: ...

... 对于受上游交叉口影响的车流,其上游调节增量延误修正系数为^[11]: ...

... 参考相关文献^[11,13],这里分析期持续时间T=1 h,k=0 ...

2008

0.0

. 2008, 21(1):83-88 DOI:doi:10.3321/j.issn:1001-7372.2008.01.015

Offset model for arterial road coordinate control and its optimization method

干道协调控制相位差模型及其优化方法

Lu Kai , Xu Jian-min.

卢凯, 徐建闽

By phase optimization design on arterial road coordinate control system, a new offset model for arterial road coordinate control was established. Authors considered all the factors, such as road average speed, traffic flow dispersion, turning traffic flow from crossway and asymmetry of vehicles arrival distribution in the model which greatly influenced the control effect of arterial road coordinate control scheme. Total delay and total parking number were taken as the offset model output, and the rules of two directional traffic flow delay at the intersections were particularly analyzed. Moreover, programming calculation of Matlab was introduced to realize the optimization of the offset. Results show that the optimized model can provide a new approach for offsets optimization of arterial road coordinate control system.

通过对协调控制系统进行相位优化设计, 综合考虑各路段的平均车速、车流的离散性、相交道路的转弯车流以及车辆到达的不均匀性等各种影响干道协调控制方案实施效果的主要因素后, 建立了一种新的干道协调控制相位差模型。以干道控制系统的总延误与总停车次数作为相位差模型的输出, 对上、下行车队在交叉口的延误规律进行了分析, 并利用Matlab编程计算来实现相位差的优化。结果表明:该优化模型为解决干道协调控制相位差优化问题提供了一种新方法。

... 在表1所示的单点信号配时参数的基础上,用已有相位差优化方法可得交叉口b相对于交叉口a的协调相位的绿时差分别为51 s和78 s^[12] ...

2009

0.0

... 参考相关文献^[11,13],这里分析期持续时间T=1 h,k=0 ...