信号交叉口车辆排队长度是交通服务水平和路网运行效率评价的主要依据, 也常用作交通信号设计的依据。根据用途及数据来源不同, 排队长度可分为预测值和估算值, 分别应用于交通信号设计和交通运行状况评价。排队长度的研究通常采用概率论、排队论、波动论、累计曲线图解法、神经网络等方法进行, 这些方法均能够在一定范围内描述交通排队现象, 并构建相应的排队长度计算模型^{[1, 2, 3, 4, 5]}。姚荣涵等^[6]在上述传统方法基础上, 借鉴城市交通二流理论, 通过将实际交通流转化为阻塞交通流和行驶交通流来构建路段当量排队长度计算模型, 并利用VISSIM仿真数据验证了模型的有效性。Tian和Kyte^[7]结合18个交叉口的实际数据, 分析比较了HCM 2000中应用于双向停车控制交叉口的理论模型及作者提出的2个具有实证基础的经验模型, 在全向停车控制交叉口排队长度计算中的应用价值。荣建等^[8]则针对北京市交通的实际情况, 以SIGNAL94为基本模型建立了适合北京市交通特性和动态计算的排队长度优化模型, 但模型要求初始条件是排队长度为零。对于排队长度计算模型有效性的验证一般采用与仿真或实测数据对比的方法, 由于仿真过程往往忽略一些实际影响因素, 因此与实测数据对比验证更为可靠。无论是传统经典模型及其修正模型还是根据新理念方法提出的模型大多存在一些缺陷, 如模型某些参数(初始排队、交通流密度等)实际难以检测获得、模型适用范围受限制等。近年来也出现了采用图像处理技术对排队长度进行实时检测的研究^[9]和采用线圈检测数据搜索排队尾部车辆的研究^[10], 但出于投入成本等考虑不可能在每个需要获得排队长度的地点安装相应设备, 因此排队长度的预测和估算仍是非常必要的。现有排队长度研究的数据还是以单一来源为主, 这在一定程度上限制了计算模型的应用, 也降低了预测或估算的精确度。

信息通讯技术的进步和智能交通运输系统的发展使得获得源源不断的交通检测数据成为可能, 而且数据日益呈现多源性, 包括磁频检测数据、波频检测数据、视频检测数据、浮动车数据等, 如何综合利用这些数据进行研究成为交通领域的重要关注点。在排队长度研究方面, 更好地利用多源数据有利于弥补已有模型存在的缺陷, 也有利于引入一些新的研究理念与方法。Comert等^[11]已开始采用浮动车数据等进行排队长度估算的研究, 利用条件概率分布推导了排队长度计算模型。Ban等^[12]利用浮动车搜集到的信号交叉口行程时间(或延误)进行排队长度估算的研究。

本文主要以传统经典模型为基础, 综合利用浮动车数据、磁频检测(线圈)数据进行信号交叉口排队长度估算方法的研究, 克服单一数据来源条件下排队长度计算模型应用受限的缺陷。

由于不可能也无必要对每个交叉口的排队长度进行实时检测, 因此评价排队长度时往往依靠一些成熟的模型估算获得, 模型中的参数一般应当容易通过交通检测设备直接获取。Highway Capacity Manual 2000(HCM 2000)采用的排队长度计算模型如式(1)~(3)所示^[13]。该模型各参数意义明确, 应用广泛, 是排队长度计算的经典模型。

Qm=Q1+Q21Q1=PF2vLC3600(1-gC)1-min(1.0, XL)(gC)2Q2=0.25cLT(XL-1)+QbLcLT+(XL-1)+QbLcLT2+8kBXLcLT+16kBQbL(cLT)23

式中:Q_m为信号周期内从停止线开始, 车道组中任一条车道上车辆排队的最大长度(假定车道组中所有车道上排队长度相等), 单位为辆; Q₁为排队长度第一项, 单位为辆; Q₂为排队长度第二项, 单位为辆; PF₂为信号联动影响修正系数, 按照式(8)计算; v_L为车道组中每条车道的流率, 单位为辆/h; C为信号周期长度, 单位为s; g为有效绿灯时间, 单位为s; X_L为流率与通行能力之比(v_L/c_L); c_L为车道组中每条车道通行能力, 单位为辆/h; T为分析时段长度, 单位为s; k_B为第二项修正系数, 与车辆早期到达有关; Q_bL为分析时段开始时车道组中每一车道的初始排队长度, 单位为辆。

模型中, Q₁为假定车道组车辆均匀到达并对信号联动影响修正得到, 是红灯时间到达车辆数和车队离去前绿灯时间到达车辆数; Q₂为交通流随机特性和信号控制暂时失效引起的溢流排队, 包含分析时段开始时的初始排队。无初始排队时, Q₂可以看作一个周期溢出排队车辆数的近似值。模型参数v_L可通过交通检测器得到, 但初始排队长度Q_bL的获取往往是个难题, 一般只能通过现场观测, 或者需要连续分析几个时段并保证第一个时段无初始排队, 大大限制了该模型的应用。

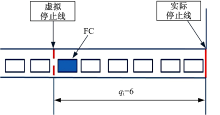
以往单一数据来源条件下, 很难解决HCM 2000模型中初始排队Q_bL难以获取的问题。本文考虑综合利用浮动车数据、检测线圈数据进行排队长度的估算。如图1所示, FC代表浮动车, 其他为一般车辆。在浮动车后划定一条虚拟停止线, 排队长度的估算分成两部分进行:实际停止线到虚拟停止线部分采用浮动车提供的GPS定位数据; 虚拟停止线上游部分可视为从虚拟停止线开始无初始排队的情况, 采用HCM 2000模型估算。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 利用多源数据估算排队长度方法示意图Fig.1 Schematic diagram for queue length estimation based on multi-source data

浮动车数据可提供每隔一定检测时间间隔的GPS定位数据及对应的时刻, 研究显示浮动车提供的GPS定位数据可精确到3 m^[14]。结合GPS定位数据、浮动车后续走行方向(可用以判定浮动车所属车道组), 可准确定位浮动车位置, 再结合标准车辆长度、停车车头空距, 即可得出实际停止线到虚拟停止线部分的排队长度, 图1中这部分排队长度q_i=6。虚拟停止线上游部分排队长度采用HCM 2000模型估算, 其中流率采用检测线圈数据, 由于以虚拟停止线作为估算的停止线, 为此必须对部分参数进行调整。

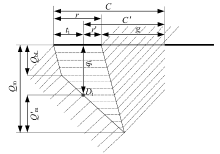
以1个信号周期作为分析时段长度、以红灯启亮时刻作为分析时段开始, 进行排队长度估算模型的研究, 有利于更加细致地分析交叉口车辆具有的周期性到达-驶离行为及排队行为。图2为1个信号周期内交叉口某一车道组车辆到达-驶离情况及排队形成-消散情况示意图。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 交叉口某一车道组车辆排队长度示意图Fig.2 Schematic diagram for queue length of a lane group in an intersection

图2中, r为有效红灯时间, 单位为s。圆点所在车辆轨迹线代表浮动车到达-驶离行为, 定义D_i为红灯期间到达的浮动车排队状态变量:

Di(qi, ti)(4)

式中:q_i为从停止线开始, 截至浮动车为止的排队长度(实际停止线到虚拟停止线部分排队长度), 单位为辆; t_i为从分析时段开始到浮动车到达时刻的时间长度, 单位为s。

结合图1、图2可知, 排队长度分两部分进行估算, 如式(5)所示:

Qm=Q'm+qi5

式中:Q'_m为信号周期内从虚拟停止线开始, 车道组中任一条车道上车辆排队的最大长度, 单位为辆。

Q'_m采用HCM 2000模型进行估算, 由于是从虚拟停止线开始估算, 故部分参数需作调整。调整后的信号周期长度为:

C'=C-ti6

调整后的有效红灯时间为:

r'=r-ti7

根据HCM 2000, 排队长度第一项中信号联动影响修正系数PF₂按式(8)计算:

PF2=(1-RPgC)(1-vLsL)(1-gC)1-RP(vLsL)8

式中:R_P为成队列行驶的车辆比例P(C/g); s_L为车道组中每条车道的饱和流率, 单位为辆/h。

由于是从虚拟停止线开始估算, v_L、C、R_P均有变化调整, 相应的PF₂计算值也发生变化, 得到PF'₂。

这里只采用红灯期间到达的浮动车数据进行排队长度的估算, 以保证PF'₂计算式分母中调整后的有效绿灯时间g'< C', 避免出现g'=C'导致分母为0的情况。容易看出, 在只采用红灯期间到达浮动车数据进行估算的情况下, g'=g。

从虚拟停止线开始车辆排队的最大长度Q'_m计算方法如式(9)~(11)所示。

Q'm=Q'1+Q'29Q'1=PF'2v'LC'3600(1-gC')1-min(1.0, X'L)(gC')10

Q'₂为初始排队为0的情况, 计算方法见式(11)。

Q'2=0.25cLT(X'L-1)+X'L-12+8kBX'LcLT11

式中:v'_L为车道组中每条车道浮动车后的流率, 单位为辆/h; X'_L为浮动车后的流率与通行能力之比(v'_L/c_L)。

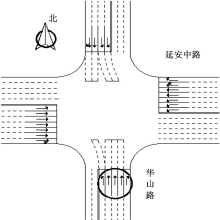
本文选取上海市中心城区延安中路-华山路交叉口南进口道进行模型的实证研究, 选取2012年7月14日13∶ 00~14∶ 00时的数据进行分析。研究对象见图3中所圈部分, 相关基本情况如下:交叉口信号周期长度为189 s; 南进口道直行车道组绿灯时长为38 s; 南进口道左转车道组绿灯时长为24 s; 黄灯时长为3 s。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 延安中路-华山路交叉口示意图Fig.3 Schematic diagram for intersection of Middle Yan'an Road vs.Huashan Road

实证研究所需利用的多源检测数据及用途如表1所示, 其中最大排队长度、初始排队长度利用SONY HDR-CX180E HD型数码摄像机拍摄并通过人工识别得到, 每条车道流率由磁频检测线圈检测得到, 红灯期间到达的浮动车的排队状态变量由实验浮动车GPS定位数据提供。每条车道的饱和流率、通行能力则事先根据实测数据标定。

表1

Table 1

表1(Table 1)

表1 实证研究所需采集数据汇总 Table 1 Required data for empirical study 数据名称 用途 信号周期内从停止线开始车辆排队的最大长度Qm 与模型计算值对比 分析时段开始时车道组中每一车道的初始排队长度QbL 用于HCM 2000模型计算 车道组中每条车道的流率vL 用于HCM 2000模型计算 车道组中每条车道浮动车后的流率v'L 用于本文模型计算 红灯期间到达的浮动车的排队状态变量Di(qi, ti) 用于本文模型计算

表1 实证研究所需采集数据汇总 Table 1 Required data for empirical study

由于右转车道无专用相位控制, 故选择直行、左转车道组进行分析。图4为实际采集到的各周期直行、左转车道平均到达流率及直行、左转车道平均最大排队长度。

由图4中可以看出:直行车道的各周期平均到达流率较左转车道更为稳定, 在220~405 辆/h的区间波动, 而左转车道各周期平均到达流率则在105~485 辆/h的区间波动。直行车道平均最大排队长度在5.5~14辆区间波动, 左转车道平均最大排队长度则在4~20辆区间波动, 可见直行车道平均最大排队长度更为稳定。

图4

Fig.4

	Figure Option ViewDownloadNew Window
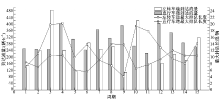	图4 各周期直行、左转车道平均到达流率及平均最大排队长度Fig.4 Average arrival flow rate and average maximum queue length of direct through lanes and left turn lanes of different cycles

根据采集到的车道组到达流率和浮动车定位数据, 按照本文模型可计算出从停止线开始车辆排队的最大长度Q_m, 由于红灯期间可能有多辆浮动车到达, 对应有多个D_i(q_i, t_i), 按照每辆浮动车分别计算可得到多个Q_m值。

为分析模型的精确度, 定义E为模型计算值相对于观测真实值的相对误差, 如式(12)所示:

E=QmO-QmEQmO×100%(12)

式中:E为模型计算值相对误差; Q_mO为观测到的从停止线开始车辆排队的最大长度真实值, 单位为辆; Q_mE为用模型计算得到的从停止线开始车辆排队的最大长度估算值, 单位为辆。

图5、图6分别为各周期直行、左转车道平均最大排队长度模型计算值相对误差的变化趋势, 同一类型的点代表一个周期内按照不同浮动车计算的平均最大排队长度估算值的相对误差, 每一周期以5 s为间隔进行研究。由于浮动车数量有限, 相对误差点分布较为稀疏, 故采用分段线性拟合表征相对误差的变化趋势, 15条曲线代表15个不同周期内相对误差的变化。由于0时刻没有浮动车到达, 所以0时刻的值取传统HCM 2000模型计算的平均最大排队长度估算值的相对误差。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 各周期直行车道平均最大排队长度估算值相对误差变化趋势Fig.5 Trend of estimated value relative errors for average maximum queue length of direct through lanes of different cycles

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 各周期左转车道平均最大排队长度估算值相对误差变化趋势Fig.6 Trend of estimated value relative errors for average maximum queue length of left turn lanes of different cycles

从图5、图6中可以看出:直行车道较左转车道拟合结果更好, 这主要是由于直行车道的各周期平均到达流率较左转车道更为稳定。随着浮动车在红灯期间内到达时间的后移, 平均最大排队长度估算值的相对误差整体呈下降趋势, 即选取红灯期间内到达时间相对较晚的浮动车进行计算, 模型的计算精确度较高; 同时, 在红灯时间的中期平均最大排队长度估算值的相对误差比较稳定。图6中部分曲线后期呈一定程度的上升趋势, 这主要是由于左转车道到达流率不稳定所致。

为排除到达流率不稳定造成的干扰, 选取多个周期模型计算值相对误差的平均值进行分析。图7为15个不同周期本文模型计算值相对误差平均值的拟合曲线, 图中点为按照本文模型以5 s为分析时间间隔计算的15个周期平均最大排队长度估算值相对误差的平均值, 由于相对误差点分布较密, 采用3次拟合曲线。直线为15个周期按照传统HCM 2000模型计算的平均最大排队长度估算值相对误差的平均值。

图7较图5、图6更加清晰, 表明:本文模型计算值的相对误差普遍小于传统HCM 2000模型计算值的相对误差, 且本文模型计算值的相对误差随浮动车在红灯期间内到达时间的后移呈现出较快下降→ 平稳→ 较慢下降的趋势。可以看出, 本文模型具有较传统经典模型更高的有效性和准确度。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 本文所提出模型与传统HCM2000模型计算相对误差比较Fig.7 Comparisons of relative errors between proposed model and traditional HCM 2000 model

提出了多源数据条件下信号交叉口排队长度估算方法, 克服了基于单一来源交通检测数据的限制, 以传统经典HCM 2000模型为基础, 综合利用浮动车数据和检测线圈数据, 通过划定虚拟停止线, 将排队长度分为两部分计算, 有效解决了初始排队长度难以获取导致的限制。实证分析发现, 本文模型具有较高的有效性和准确度, 用该模型计算得到的排队长度可用来评价交通运行状况, 从而为交通管理、控制、规划等提供决策依据。模型计算需利用红灯期间到达浮动车的排队状态信息, 本文从理想环境出发, 实验浮动车数量较大, 每个周期均有多辆浮动车可用于计算。而实际应用中, 模型计算必须保证分析时段至少1辆红灯期间到达的浮动车排队状态信息可用, 因此浮动车的合理比例等问题还有待进一步研究。