以跨径比和横隔板数目为参数, 设计了6片钢-混凝土简支曲线组合梁, 试验梁参数见表1, 跨度及截面尺寸见图1, 各试验梁沿跨度方向设置不同数量的横隔板, 厚6 mm。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 试验梁截面尺寸Fig.1 Dimension of test beams

表1

Table 1

表1(Table 1)

表1 试验梁参数 Table 1 Design parameters of test beams 序号 编号 计算跨度 L/m 曲线半径 R/m 跨径比 L/R 横隔板 数量 1 SCB 6 直线梁 直线梁 5 2 CCB12 6 60 0.1 2 3 CCB13 6 60 0.1 3 4 CCB15 6 60 0.1 5 5 CCB25 6 30 0.2 5 6 CCB55 6 12 0.5 5

表1 试验梁参数 Table 1 Design parameters of test beams

表1中各梁横隔板的位置为:2块横隔板分别设置在梁端支座处; 3块横隔板分别设置在两个梁端及跨中处; 5块横隔板分别设置在支座、跨中和两个1/4跨度处。

钢梁均采用Q235钢, 混凝土板采用C30混凝土; 纵筋与箍筋采用Φ 6HPB235钢筋, 纵筋横向间距120 mm, 配筋率0.81%; 箍筋纵向间距100 mm, 配箍率0.27%。栓钉直径13 mm, 高50 mm, 布置在钢梁腹板上方, 每列34个, 每片梁布置两列, 共68个, 均为完全连接。

各试验梁均采用跨中加载。荷载分级施加, 初期每10 kN荷载记录一次数据, 并实时记录跨中截面的荷载-挠度曲线, 当曲线斜率开始发生变化时, 荷载等级减小为5 kN。在支座截面布置滑移测点, 在L/8、L/4、3L/8和跨中截面(为避开加载位置, 偏移20 cm)布置应变、竖向位移、径向位移及滑移测点。加载布置图见图2。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 加载布置图Fig.2 Test setup

支承条件为一端设固定铰支座, 一端设活动铰支座, 每个支座下方均在钢梁腹板位置设置传感器以测试支座反力。CCB55梁由于跨径比较大, 在曲线内侧支座出现负反力, 因此设计了反力架, 将曲线内侧支座传感器设置在腹板上方, 其他5片试验梁及CCB55梁曲线外侧的支座传感器均设置在腹板下方。

由于模型试验中测点数量有限, 且结果会在一定程度上受到试验误差的影响, 因此采用ANSYS有限元软件对6片试验梁加载全过程的受力特性进行数值模拟, 对试验结果进行补充和校核。

1.3.1 模型参数

有限元模型中混凝土的受压本构模型按《混凝土结构设计规范》(GB50010-2002)附录C.2.1条的规定选用。钢梁、纵筋和箍筋的本构关系模型均采用弹性模型, 弹性模量均取E_s=2.06× 10⁵ MPa。

对钢梁上下翼缘板(厚8 mm)和腹板(厚6 mm)各制作3个标准拉伸试件, 测得试件的平均屈服强度和极限拉伸强度分别为245.53 MPa和379.53 MPa(8 mm)、292.77 MPa和429.1 MPa(6 mm)。钢筋未进行材性试验, 计算中采用规范标准值, 即235 MPa。SCB、CCB12、CCB13、CCB15、CCB25、CCB55梁混凝土板实测抗压强度分别为31.7、32.7、32.4、31.1、31.9、32.8 MPa。

栓钉的荷载-滑移关系采用式(1)表示^[14]:

Q=Qu(1-e-0.7s)0.41

式中:Q为栓钉承受的剪力; s为结合面上的相对滑移; Q_u为单个栓钉的极限承载力。

根据试验梁的钢梁尺寸和混凝土板厚制作了3个推出试件, 得到单个栓钉的平均极限承载力为50.83 kN。

1.3.2 有限元模型

有限元模型中混凝土板采用SOLID65单元, 钢梁采用SHELL43单元, 钢筋采用LINK8单元, 栓钉采用COMBIN39弹簧单元。将钢梁和混凝土板在每个栓钉位置处的相应节点, 采用两个水平方向(切向和径向)的COMBIN39弹簧单元进行连接, 通过其实常数中的位移-力曲线分别定义两个水平方向的荷载-滑移曲线, 以模拟结合面的切向滑移和径向滑移。由于竖向掀起变形很小, 故将钢梁和混凝土板在每个栓钉位置处的相应节点竖向耦合。

模型一端限制其径向位移、竖向位移, 另一端限制其竖向位移、切向位移和径向位移。加载时将跨中集中力等效为跨中截面混凝土板上的线荷载。

不同跨径比和横隔板数的试验梁, 其全过程受力特征均经历了弹性阶段— 弹塑性阶段— 塑性阶段的发展过程。6片梁在破坏时均表现为钢梁下翼缘受拉屈服, 加载点附近混凝土板压碎, 没有出现滑移破坏特征。除直线的SCB梁以外, 其他曲梁破坏时的挠度均为曲线外侧大, 内侧小, 出现弯扭破坏特征, 跨径比越大, 扭转效应越明显(见图3)。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 试验梁破坏Fig.3 Failure of test beam

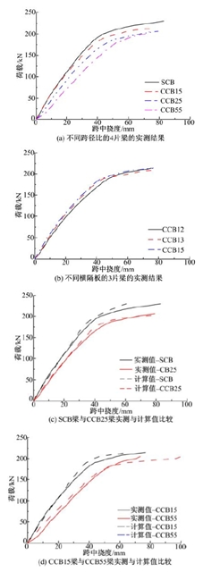
各试验梁跨中截面的荷载-挠度曲线的比较见图4。

由图4可以看出:

(1)试验梁的抗弯刚度、极限荷载和屈服荷载均随跨径比的增加逐渐减小, 说明跨径比的增大使曲线组合梁抗弯刚度下降, 承载力降低。

(2)横隔板数目的不同对试验梁的整体弯曲受力性能影响不大, 但只有两个端横隔板的CCB12梁的刚度较其他两片有中横隔板的CCB13和CCB15梁略有减小; 而CCB13和CCB15梁之间则几乎没有差别。

(3)有限元计算结果与实测结果吻合较好, 可以采用计算结果对试验结果进行相互校核和补充。

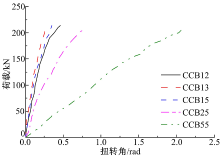
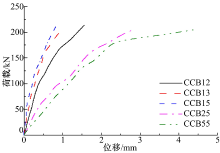
5片曲线组合梁跨中截面的荷载-扭转角和荷载-径向位移实测曲线如图5和图6所示。

由图5和图6可知, 相同荷载下, 跨中截面扭转角和径向位移均随跨径比的增大而增大, 说明截面抗扭刚度随跨径比的增大而减小; 跨径比均为0.1, 但横隔板数目不同的3片梁的扭转角和径向位移曲线都比较接近, 随着横隔板数量的增加, 跨中截面扭转角和径向位移均随之减小, 说明抗扭刚度有所增加, 但不明显。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 跨中荷载-挠度曲线Fig.4 Load-vertical deflection curve at middle span

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 跨中荷载-扭转角曲线Fig.5 Load-twist angle at middle span

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 跨中荷载-径向位移曲线Fig.6 Load-radial deflection at middle span

分析横隔板数相同(均为5块), 跨径比不同的4片试验梁(SCB、CCB15、CCB25、CCB55), 在50 kN跨中集中荷载作用下, 钢梁底板和混凝土板上表面切向及径向应变沿截面横向的分布规律。

2.2.1 切向应变

在跨中、L/4、3L/8和L/8截面处, 沿截面横向钢梁底板切向应变的实测值和计算值见图7。混凝土板上表面切向应变的实测值和计算值见图

8, 各图中实测值在跨中截面为距其20 cm处的结果。图中横坐标y表示横截面上混凝土上表面或钢梁底板距曲线内侧边缘的距离, 以下同。

在图7和图8中的4个截面中, 各梁在跨中和L/4截面均设有横隔板, 3L/8和L/8截面处没有横隔板, 实测值中距跨中20 cm处也没有横隔板。与试验结果相比, 有限元结果虽有一定误差(由测量误差和计算模型误差导致), 但结果较为接近, 且与实测结果表现出相同的横向分布规律, 具体为:

(1)钢梁底板和混凝土上表面的切向应变实测值在L/4截面、计算值在L/2和L/4截面, 即在有横隔板处均表现为曲线内侧小、外侧大, 这一点与一般曲梁的弯扭耦合特征相同; 但实测值在距跨中20 cm处、3L/8截面和L/8截面、计算值在3L/8截面和L/8截面, 即在无横隔板处则为内侧大、外侧小, 与有横隔板处相反。

(2)在有横隔板的跨中截面和L/4截面, 钢梁底板的切向应变因受横隔板的影响, 有限元计算值均呈现两端大、中间小的U形, 但从整体上看还是内侧小、外侧大, 这种U形分布在实测结果中由于测点较少没有表现出来; 在没有横隔板的3L/8截面和L/8截面, 有限元计算结果则均比实测结果表现出更明显的线性分布特征。

(3)无论有无横隔板, 计算结果与实测结果均表现出切向应变随跨径比的增大而增大。

根据以上结果进行讨论: 有无横隔板处之所以切向应力沿截面横向的分布规律相反, 是由于曲线组合梁在竖向荷载下除产生竖向变形外, 还产生扭转变形和径向变形, 而横隔板在扭转和径向变形过程中起到了一种弹性约束的作用, 在有横隔板的位置, 由于弹性约束的影响切向应力增大, 而无横隔板的位置处于相邻两个横隔板产生的弹性约束之间, 反而有一种“ 卸载” 的趋势, 如同处于两个支座之间的跨中部位, 这种现象在曲线外侧和曲线内侧正好相反, 因此出现有横隔板处切向应力在曲线内侧小、外侧大, 而无横隔板处则内侧大、外侧小。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 钢梁底板切向应变沿横截面的分布Fig.7 Transverse distribution of tangential strain at the bottom of steel girder

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 混凝土上表面切向应变沿横截面的分布Fig.8 Transverse distribution of tangential strain at the top of concrete slab

2.2.2 径向应变

上述几个截面钢梁底板的径向应变实测值及计算值见图9。

由图9可知, 钢梁底板径向应变的有限元计算结果与实测结果数值接近。与切向应变相同, 沿截面横向均表现出有横隔板处内侧小、外侧大, 无横隔板处内侧大、外侧小, 且有限元计算结果在有横隔板处更明显地表现出两端大中间小的U形分布, 无横隔板处则近似为直线分布; 无论有无横隔板, 钢梁底板的径向应变均随曲梁跨径比的增大而增大。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 钢梁底板径向应变沿横截面的分布Fig.9 Transverse distribution of radial strain at bottom of steel girder

2.3.1 切向滑移

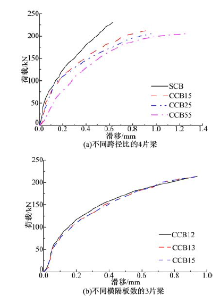
各试验梁在L/8截面(该截面滑移较大)曲线外侧钢梁与混凝土板结合面上的切向滑移实测值随荷载的变化规律如图10所示。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 荷载-切向滑移曲线Fig.10 Load-tangential slip curve at L/8 section

各试验梁的切向滑移沿梁轴向的分布规律如图11所示, 图中横坐标x表示距梁端的距离。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 切向滑移沿轴向的分布Fig.11 Axial distribution of tangential slip

由图11可以看出:

(1)各试验梁切向滑移沿梁轴向的分布规律基本相同。由于切向滑移是栓钉受到钢梁与混凝土板结合面上的水平剪力所致, 而结合面水平剪力和梁截面竖向剪力之间存在线性关系, 因此试验梁切向滑移沿梁轴的分布规律与承受跨中集中荷载时梁的竖向剪力基本相同, 但由于支座处的反力增加了混凝土板与钢梁结合面上的局部压力, 使摩擦力增大, 抑制了该处的滑移, 因此梁端滑移反而较小。

(2)相同荷载下, 跨径比最大的CCB55梁滑移量最大; 横隔板数对切向滑移的影响不明显。

2.3.2 径向滑移

由于径向滑移较小, 误差相对较大, 因此试验中测得的径向滑移没有表现出明显的规律, 因此只列出径向滑移计算结果沿梁轴向的分布, 见图12。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 径向滑移沿轴向的分布Fig.12 Axial distribution of radial slip

由图12可知:

(1)与切向滑移相比, 径向滑移数值很小, 但在横隔板位置均产生突变, 数值较大, 这是由于径向滑移是结合面上下相应位置钢梁与混凝土板径向位移的差值, 而钢梁的径向位移直接受横隔板径向约束的影响, 数值较小, 但混凝土板受横隔板径向约束较小, 因此二者的差值较大, 在横隔板处出现突变。

(2)随跨径比的增大, 试验梁的径向滑移随之增大, 跨径比均为0.1的3片梁径向滑移基本相同, 但随着横隔板数量的减小, 径向滑移也随之增大。