液压传动技术日趋广泛的应用促使液压设备和元件迅速发展, 同时也对液压泵的流量和压力, 马达的转矩和转速, 元件的噪声、效率、寿命、抗冲击性、比功率、控制方式等方面提出了越来越高的要求^[1]。目前国内外的研究人员大都基于现有液压泵或马达的原理, 致力于提高元件性能, 改善各部件的材料、润滑条件, 提高元件寿命^{[2, 3, 4]}。在泵和马达的工作原理上深入研究的人员却很少。

双定子多速马达由一个转子对应两个定子, 有等宽的内外定子曲线, 故其有无需回程装置、叶片不脱空、比功率大、可多级调速和多级调扭矩、实现差动等优点^{[5, 6, 7, 8]}。该双定子马达可取代一系列中低压马达, 广泛应用于汽车、船舶、工程机械等领域。

传统的叶片式泵或马达都是通过压力平衡的方式减小叶片尖端对定子曲面的压力, 作者换了一个思路:若叶片尖端与定子曲线的运动副为滚动, 用滚压代替滑压, 同样可减少磨损。本文对滚柱叶片在双定子多速马达中密封容积的形成、间隙补偿的机理进行了理论研究和实验验证。

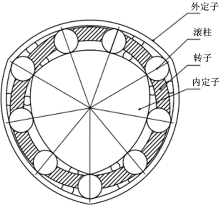
图1所示为滚柱式双定子多速马达, 该结构类似于滚子轴承, 虽不易磨损但无补偿能力, 并且滚柱的直径直接限制了马达的排量, 影响了其比功率。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 滚柱式双定子马达Fig.1 Roller type double-stator motor

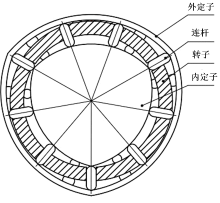
图2所示为连杆式双定子多速马达, 该结构可实现更大的排量, 提高了比功率, 但连杆圆头磨损后无法实现径向磨损补偿, 且对定子曲线磨损较严重。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 连杆式双定子马达Fig.2 Rectangle vane type double-stator motor

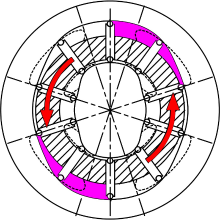
图3为滚柱叶片式多速马达, 其综合了滚柱式与连杆式的优点,

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 滚柱叶片式双定子马达Fig.3 Roller tip-vane type double-stator motor

又解决了两者的不足。滚柱5与连杆4组成了连杆滚柱组, 滚柱在连杆凹槽与内、外定子曲线的包围下, 不会掉出。当通入高压油后, 在油液压力与离心惯性力的推动下, 滚柱产生偏心, 同时压紧定子曲线与连杆凹槽, 形成了马达的密封容积。叶片尖端与内定子外表面、外定子内表面间存在滚动, 将叶片与定子曲线间磨损这一矛盾转化为滚柱与连杆的矛盾。与滚柱式结构相比, 其能够实现更大的排量, 增大了比功率; 与连杆式结构相比, 其对内外定子的定子曲线为滚动, 对定子曲线磨损更小, 且能够实现径向间隙自动补偿。

总的来说, 这种滚柱叶片的双定子多速马达具有对定子曲线要求低, 径向间隙能够补偿, 密封性好等优点。

传统的叶片式液压泵是将高压油引入叶片底部, 靠油液压力、离心惯性力将叶片尖端紧贴并跟随在定子曲线上, 对于叶片式马达而言, 还需要回程装置^[9]。该新型的液压马达, 由于具有内外两个定子和等宽的定子曲线, 叶片无需回程, 故其密封容积的形成机理与传统叶片式泵、马达有着本质的区别。这里以双作用双定子多速马达为例, 通过对马达的双滚柱连杆结构的受力分析, 阐明滚柱叶片式双定子多速马达形成密封容积与间隙补偿的机理。

2.1 马达在不同工作方式下叶片的受力状态

双作用双定子多速马达有4种工作方式, 分别为:外马达单独工作、内马达单独工作、内外马达联合工作、内外马达差动工作。不同工作方式下叶片的受力状态也不同, 并且通过不同工作方式的切换可实现多级定转速与多级定转矩。

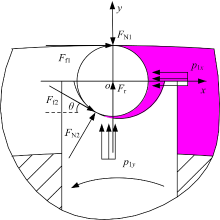
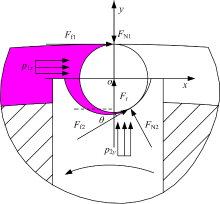
(1)内马达单独工作如图4所示, 此时外马达通低压油卸荷, 内马达中的油液压力作用在叶片内端, 与离心惯性力一起, 使叶片尖端压紧外定子曲线。此时外马达中与内马达高压油区相对的外定子内表面受叶片顶端正压力较大。

(2)外马达单独工作如图5所示, 此时内马达通低压油卸荷,

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 内马达单独工作Fig.4 Inner motor working

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 外马达单独工作Fig.5 Outer motor working

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 内外马达联合工作Fig.6 Unite working

外马达中的油液压力作用在叶片外端, 其与离心惯性力之差, 使叶片尖端压紧内定子。此时内马达中与外马达高压油区相对应的内定子外表面受叶片顶端正压力较大。

(3)内外马达联合工作如图6所示, 此时内外马达同时正向通入高压油, 外马达的油液压力作用在叶片外端, 与离心惯性力一起, 使叶片尖端压紧内定子外表面; 内马达的油液压力作用在叶片内端, 与离心惯性力一起, 使叶片尖端压紧外定子内表面; 处于内、外定子曲线大、小圆弧上的叶片, 所受的内、外马达液压力相互抵消。此时, 内、外马达排油区定子过渡曲线受叶片顶端正压力较大。

(4)内外马达差动工作如图7所示, 此时内外马达同时反向通入高压油, 马达按箭头方向旋转, 内、外马达作用在叶片两端的油液压力相互抵消。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 内外马达差动工作Fig.7 Differential working

分析以上4种工况可得:内、外马达单独或联合工作时, 都会出现叶片尖端对定子曲面作用力较大的情况, 而对于这种将叶片尖端设计为滚柱的结构, 可减少内、外马达单独或联合工作时, 叶片尖端与内、外马达低压区定子曲线的相对滑动, 进而可减少磨损。又由于外马达排量较大, 当外马达通入高压油后马达转子的运动方向总与外马达相同, 而内马达则实现了泵的功能。当外马达通入高压油后, 处于高低压油分界处的外端滚柱有两种工作状态, 位置分别处于定子曲线大、小圆弧上; 当内马达通入高压油后, 处于高低压油分界处的内端滚柱有4种不同的工作状态, 位置分别处于差动或一般工作方式下的定子曲线大、小圆弧上。

2.2 密封容积与间隙补偿

2.2.1 外马达密封容积的形成

外马达组通入高压油后, 处于高低压分界处的滚柱在油液压力与离心惯性力的推动下, 产生偏心, 压紧外定子与连杆凹槽, 这样滚柱、连杆、转子、外定子与左右侧板组成了外马达的密封容积。根据上节分析, 下面是对外马达中处于高低压油分界处滚柱的两种工作状态的受力分析。

(1)转速稳定处于外定子曲线大圆弧段上时, 滚柱受力如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 外定子大圆弧处滚柱受力Fig.8 Forces analysis of roller on major arc of inner ring of outer stator

假设运转稳定时润滑良好, 不计滚动摩阻, 油液不可压缩且定子曲线圆弧半径远大于滚柱半径。根据达朗贝尔原理可得:

FN1=FN2·cosθ-Ff2sinθ+Fr+p1y1

式中:p_1x、p_1y分别为液压力x、y方向的分力; F_r为离心惯性力; F_f2为摩擦力。

由式(1)得, 在压力、转速较高, 摩擦因数较小时F_N2处为滑动摩擦, 可推出:

FN1=pBrsinθ+ω2l1m+pBr1+cosθcosθ-u2sinθsinθ+u21+cosθFN2=pBr1+cosθsinθ+u21+cosθ2

式中:p为油液压力; B为连杆宽度; u₂为连杆凹槽处滑动摩擦因数; r为滚柱半径; l₁为外定子曲线大圆弧半径与滚柱半径之差; m为滚柱质量; ω 为转子角速度。

控制好各接触面的摩擦因数, θ 角可以在一定范围内变化, 进而形成密闭容积。

(2)转速稳定、滚柱处于外定子曲线小圆弧段上时, 滚柱受力如图9所示。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 外定子小圆弧处滚柱受力Fig.9 Forces analysis of roller on minor arc of inner ring of outer stator

推导可得:

FN1=pBrsinθ+ω2l2m+pBr1+cosθcosθ+u2sinθsinθ-u21+cosθFN2=pBr1+cosθsinθ-u21+cosθ3

式中:l₂为外定子小圆弧半径与滚柱半径之差。

比较式(2)与式(3), 由于高压油与外定子对滚柱的摩擦力方向一致, 滚柱在小圆弧上时所受正压力更大, 应首先满足大圆弧上的密封。

2.2.2 内马达密封容积的形成

(1)当内、外马达处于差动工作状态时

转速稳定且连杆滚柱处于内定子曲线大圆弧上时, 滚柱受力如图10所示。

图10

Fig.10

	Figure Option ViewDownloadNew Window
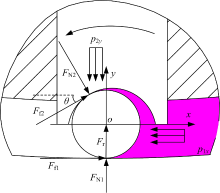	图10 差动时内定子大圆弧处滚柱受力Fig.10 Forces analysis of roller on major arc of outer ring of inner stator with differential working connection

得出内定子曲线对滚柱的正压力, 连杆凹槽对滚柱的正压力为:

FN1=pBrsinθ-ω2l3m+pBr1+cosθcosθ-u2sinθsinθ+u21+cosθFN2=pBr1+cosθsinθ+u21+cosθ4

式中:l₃为内定子大圆弧半径与滚柱半径之差。

当滚柱处于内定子曲线小圆弧上时, 滚柱受力如图11所示。

图11

Fig.11

	Figure Option ViewDownloadNew Window
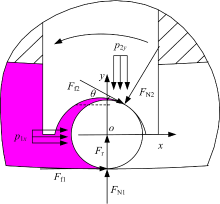	图11 差动时内定子小圆弧处滚柱受力Fig.11 Forces analysis of roller on minor arc of outer ring of inner stator with differential working connection

推导可得各接触面的正压力为:

FN1=pBrsinθ+ω2l4m+pBr1+cosθcosθ+u2sinθsinθ-u21+cosθFN2=pBr1+cosθsinθ-u21+cosθ5

式中:l₄为内定子小圆弧半径与滚柱半径之差。

(2)当内、外马达处于联合或单独工作状态时

转速稳定且连杆滚柱处于内定子曲线大圆弧上时, 滚柱受力如图12所示。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 非差动内定子大圆弧处滚柱受力Fig.12 Forces analysis of roller on major arc of outer ring of inner stator without differential working connection

推导可得各接触面的正压力为:

FN1=pBrsinθ-ω2l2m+pBr1+cosθcosθ+u2sinθsinθ-u21+cosθFN2=pBr1+cosθsinθ-u21+cosθ6

当滚柱处于内定子曲线小圆弧上时, 受力如图13所示。

图13

Fig.13

	Figure Option ViewDownloadNew Window
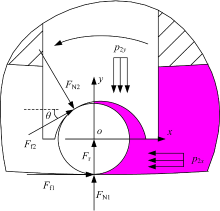	图13 非差动内定子小圆弧处滚柱受力Fig.13 Forces analysis of roller on minor arc of outer ring of inner stator without differential working connection

推导可得各接触面的正压力为:

FN1=pBrsinθ-ω2l2m+pBr1+cosθcosθ-u2sinθsinθ+u21+cosθFN2=pBr1+cosθsinθ+u21+cosθ7

比较上式并分析可得:内、外马达差动工作时, 处于内定子大圆弧上的滚柱由于摩擦力与液压力方向相反, 且受向外的离心惯性力作用, 应首先满足内定子大圆弧处的密封。

在非理想状态下, 由于油液是可压缩的, 内、外定子曲线区中会有一个预压缩过程, 内、外滚柱的偏心应该是变化的, 在液压力的作用下, 滚柱依然能够压紧各接触面实现密封。

2.2.3 间隙补偿

为了保证马达各个运动副之间能够运转平稳顺畅, 间隙不可避免, 并且在工作的过程中也会产生磨损。必须补偿磨损以保持容积效率。当以简单的圆弧为连杆凹槽曲线时, 示意图如图14所示。

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 径向补偿示意图Fig.14 Radical clearance compensation

可得一侧滚柱连杆的径向长度改变Δ S为:

ΔS=L1+L2-r=(R-r)(1-cosθ)(8)

分析式(8)可知, 极限偏角θ 和滚柱与连杆凹槽半径之差决定了马达的补偿径向间隙能力。在设计马达时合理选择凹槽圆弧与控制偏角范围能够使补偿径向间隙能力达到最优。

已加工出的双作用双定子多速马达的样机如图15所示, 样机参数如下:外马达工作时排量为80.5 mL/r, 内马达工作时排量为29.5 mL/r, 内、外马达联合工作时排量为110 mL/r, 内、外马达差动工作时排量为51 mL/r, 滚柱半径为3 mm, 连杆槽半径为3.3 mm。

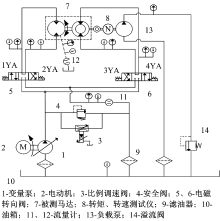
为了验证多速马达原理的正确性和马达设计的合理性, 搭建了双定子多速马达实验平台, 对马达4种不同工作状态进行了空载排量实验和效率实验。液压系统如图16所示。

图15

Fig.15

	Figure Option ViewDownloadNew Window
	图15 双作用双定子多速马达样机Fig.15 Double-acting double-stator multi-motor prototype

图16

Fig.16

	Figure Option ViewDownloadNew Window
	图16 双定子多速马达实验系统图Fig.16 Double-stator multi-motor experimental system

在双定子多速马达实验平台中, 液压马达所需的液压油由变量液压泵1提供, 通过调节比例调速阀3来改变被测马达的转速, 通过流量计11测量系统回油流量, 流量计12测量马达的泄漏流量。用电磁换向阀5、6改变供油方向, 进而实现液压马达4种不同的工作状态。转矩、转速测量仪8用于测量液压马达的输出转矩与转速。泵13和溢流阀14组成负载, 通过控制溢流阀14的溢流压力调节负载泵13的工作压力, 即控制负载的大小。通过压力表来测量液压马达的进出口压力情况。图17为双定子多速马达实验照片。

图17

Fig.17

	Figure Option ViewDownloadNew Window
	图17 双定子液压马达实验系统Fig.17 Double-stator multi-motor experimental system

根据中华人民共和国国家标准液压泵、液压马达空载排量的测定方法, 测量参数的显示值的稳态条件如表1所示。实验时应该在稳态条件下测量液压马达的压力、流量转速的显示值。

在国标GB7936-87中规定, 液压马达空载排量测定的计算公式为:

V_i=1000 N(∑j=1Nnjqv)-(∑j=1Nnj)(∑j=1Nqv)N(∑j=1Nnj2)-(∑j=1Nnj)2(9)

马达的容积效率公式为:

ηv=V1iV1e=q1i/niq1e/ne=(q2i+qdi)/ni(q2e+qde)/ne×100%(10)

式中:V_1e为实验压力下的输入排量(mL/r); V_1i为空载压力下的输入排量(mL/r); q_1i为空载压力下的输入流量(L/min); q_1e为实验压力下的输入流量(L/min); q_2i为空载压力下的输出流量(L/min); q_2e为实验压力下的输出流量(L/min); q_di为空载压力下的外泄漏流量(L/min); q_de为实验压力下的外泄漏流量(L/min); n_i为空载压力下的转速(r/min); n_e为实验压力下的转速(r/min)。

马达机械效率公式为:

ηm=TiωiΔpqt=2πTiΔpVi×100%(11)

式中:T_i为实验压力下的输出转矩(N· m); ω _i为实验压力下的输出角速度(rad/s); V_i为液压马达的排量(mL/r)。

马达的总效率公式为:

η=ηvηm12

双作用双定子多速马达的空载排量数据如表1~表5所示。

表1

Table 1

表1(Table 1)

表1 显示值的稳定条件 Table 1 Stable condition of displayed value 测量内容 允许变动范围/% A B C 转速 ± 0.5 ± 1.0 ± 2.0 流量 ± 0.5 ± 1.0 ± 2.0 压力(表压小于0.2 MPa) ± 1.0 ± 3.0 ± 5.0 压力(表压大于或等于0.2 MPa) ± 0.5 ± 1.5 ± 2.5

表1 显示值的稳定条件 Table 1 Stable condition of displayed value

表2

Table 2

表2(Table 2)

表2 外马达单独工作时的空载排量测定 Table 2 Determination of load-displacement when outside motor working alone 压力/MPa 压差 /MPa 转速/ (r· min-1) 流量/(L· min-1) 转矩 /(N· m) 进口 出口 输出 泄漏 输入 1.1 0.3 0.8 57 4.4 0.2 4.6 6.1 1.2 0.4 0.8 89 6.9 0.3 7.2 6.1 1.3 0.2 1.1 117 9.0 0.4 9.4 6.3 1.1 0.2 0.9 159 12.3 0.5 12.8 6.2 1.2 0.3 0.9 185 14.3 0.6 14.9 6.2

表2 外马达单独工作时的空载排量测定 Table 2 Determination of load-displacement when outside motor working alone

表3

Table 3

表3(Table 3)

表3 内马达单独工作时的空载排量测定 Table 3 Determination of load-displacement when inside motor working alone 压力/MPa 压差 /MPa 转速/ (r· min-1) 流量/(L· min-1) 转矩 /(N· m) 进口 出口 输出 泄漏 输入 1.2 0.3 0.9 107 3.1 0.1 3.2 2.2 1.2 0.4 0.8 68 5.3 0.2 5.5 2.1 1.1 0.2 0.9 100 7.8 0.3 8.1 2.2 1.3 0.3 1.0 139 10.8 0.4 11.2 2.2 1.1 0.2 0.9 172 13.3 0.6 13.9 2.2

表3 内马达单独工作时的空载排量测定 Table 3 Determination of load-displacement when inside motor working alone

表4

Table 4

表4(Table 4)

表4 内、外马达同时工作时的空载排量测定 Table 4 Determination of load-displacement when inside and outside motor work simultaneously 压力/MPa 压差 /MPa 转速/ (r· min-1) 流量/(L· min-1) 转矩 /(N· m) 进口 出口 输出 泄漏 输入 1.1 0.3 0.8 50 5.3 0.2 5.5 8.7 1.2 0.2 1.0 88 6.8 0.3 7.1 8.8 1.2 0.2 1.0 115 8.9 0.4 9.3 8.8 1.3 0.3 1.0 154 11.9 0.5 12.4 8.8 1.2 0.4 0.8 187 14.5 0.6 15.1 8.7

表4 内、外马达同时工作时的空载排量测定 Table 4 Determination of load-displacement when inside and outside motor work simultaneously

表5

Table 5

表5(Table 5)

表5 内、外马达差动工作时的空载排量测定 Table 5 Determination of load-displacement when inside and outside motor in differential connection 压力/MPa 压差 /MPa 转速/ (r· min-1) 流量/(L· min-1) 转矩 /(N· m) 进口 出口 输出 泄漏 输入 1.2 0.2 1.0 75 3.6 0.2 3.8 3.9 1.2 0.3 0.9 66 5.1 0.2 5.3 3.8 1.3 0.2 1.1 104 8.1 0.3 8.4 3.9 1.1 0.4 0.7 144 11.1 0.5 11.6 3.7 1.0 0.3 0.7 184 14.2 0.6 14.8 3.7

表5 内、外马达差动工作时的空载排量测定 Table 5 Determination of load-displacement when inside and outside motor in differential connection

由于人工操作等因素, 实验的空载排量与双定子多速液压马达的设计结果略有误差, 但基本一致。马达的结构特点决定外马达的排量大于内马达, 这与定子曲线有关, 当内外马达同时工作时可获得低速、大扭矩; 差动工作时可获得高速、小扭矩。

根据式(11)(12)测得液压马达在不同工况下的实验数据如表6~表10所示。

表6

Table 6

表6(Table 6)

表6 双定子液压马达空载排量 Table 6 Determination of load-displacement of double-stator motors 工况 排量/(mL· r-1) 外马达单独工作 77.3 内马达单独工作 28.6 内、外马达联合工作 105.1 内、外马达差动工作 48.6

表6 双定子液压马达空载排量 Table 6 Determination of load-displacement of double-stator motors

表7

Table 7

表7(Table 7)

表7 外马达单独工作实验数据 Table 7 Experimental data when outside motor working alone 压力/MPa 压差 /MPa 转速/ (r· min-1) 流量/(L· min-1) 转矩 /(N· m) 进口 出口 输出 泄漏 输入 1 0.2 0.8 68 5.28 0.2 5.5 6.1 2.2 0.3 1.9 89 6.89 0.31 7.2 15.0 3.1 0.2 2.9 115 8.9 0.6 9.5 24.3 4.2 0.2 4.0 135 10.5 0.8 11.3 34.8 5.1 0.3 4.8 161 12.4 1.4 13.6 43.8 6.1 0.2 5.9 179 13.82 1.7 15.2 61.3

表7 外马达单独工作实验数据 Table 7 Experimental data when outside motor working alone

表8

Table 8

表8(Table 8)

表8 内马达单独工作实验数据 Table 8 Experimental data when inside motor working alone 压力/MPa 压差 /MPa 转速/ (r· min-1) 流量/(L· min-1) 转矩 /(N· m) 进口 出口 输出 泄漏 输入 1 0.2 0.8 186 5.3 0.2 5.5 2.2 2.2 0.3 1.9 243 7.0 0.3 7.2 5.5 3.1 0.2 2.9 314 9.0 0.6 9.5 8.9 4.2 0.2 4.0 371 10.6 0.8 11.3 12.7 5.1 0.3 4.8 439 12.6 1.4 13.6 16.1 6.1 0.2 5.9 485 13.9 1.7 15.2 22.4

表8 内马达单独工作实验数据 Table 8 Experimental data when inside motor working alone

表9

Table 9

表9(Table 9)

表9 内、外马达差动工作实验数据 Table 9 Experimental data when inside and outside motor in differential connection 压力/MPa 压差 /MPa 转速/ (r· min-1) 流量/(L· min-1) 转矩 /(N· m) 进口 出口 输出 泄漏 输入 1 0.2 0.8 114 5.2 0.3 5.5 3.8 2.2 0.3 1.9 148 6.7 0.5 7.2 9.6 3.1 0.2 2.9 188 8.6 0.9 9.5 15.5 4.2 0.2 4.0 218 10.1 1.2 11.3 22.9 5.1 0.3 4.8 255 11.8 1.8 13.6 27.6 6.1 0.2 5.9 279 13.1 2.1 15.2 39.1

表9 内、外马达差动工作实验数据 Table 9 Experimental data when inside and outside motor in differential connection

表1

Table 1

表1(Table 1)

表1 0 内、外马达联合工作实验数据 Table 1 0 Experimental data when inside and outside motor work simultaneously 压力/MPa 压差 /MPa 转速/ (r· min-1) 流量/(L· min-1) 转矩 /(N· m) 进口 出口 输出 泄漏 输入 1 0.2 0.8 48 5.1 0.4 5.5 8.7 2.2 0.3 1.9 63 6.6 0.6 7.2 21.3 3.1 0.2 2.9 80 8.3 1.2 9.5 34.0 4.2 0.2 4.0 93 9.6 1.7 11.3 48.9 5.1 0.3 4.8 109 10.7 2.9 13.6 61.9 6.1 0.2 5.9 119 11.7 3.5 15.2 84.9

表1 0 内、外马达联合工作实验数据 Table 1 0 Experimental data when inside and outside motor work simultaneously

可得出多作用液压马达的效率曲线, 如图18~图20所示。

图18

Fig.18

	Figure Option ViewDownloadNew Window
	图18 液压马达容积效率曲线Fig.18 Volumetric efficiency of hydraulic motor

图19

Fig.19

	Figure Option ViewDownloadNew Window
	图19 液压马达机械效率曲线Fig.19 Mechanical efficiency of hydraulic motor

图20

Fig.20

	Figure Option ViewDownloadNew Window
	图20 液压马达总效率曲线Fig.20 Efficiency of hydraulic motor

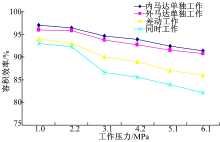
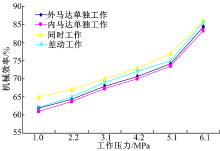
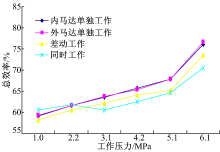
由图18可知, 压力较低时容积效率较高且下降趋势缓和, 随着压力的增加, 容积效率严重下降, 且外马达单独作用与内马达单独作用工况下的效率高于差动作用与联合作用工况。对于液压马达的总效率, 随着压力的升高, 马达的机械效率增加, 总效率相对缓慢增加。分析可知容积效率下降严重可能是受样机端面泄漏影响, 而低压时处于润滑油液里相对滑动的面之间没有形成压力油膜, 致使相对滑动件之间处于半干摩擦状态, 阻力较大, 高压工作时, 虽然运动件之间的相互作用力增大, 但是相对运动面之间形成了压力油膜, 大大降低了相对运动件之间的摩擦力, 进而提高了马达的机械效率。由此可见在控制好端面泄漏后, 采用滚柱叶片结构的双定子马达能实现更高的效率。

提出了一种新型的滚柱叶片结构, 将叶片尖端与内、外定子曲线间的滑压变为滚压, 这种滚柱叶片式结构将叶片尖端与定子曲线间磨损的矛盾转移到了滚柱与叶片凹槽, 避开了复杂的定子曲线, 能够实现径向间隙补偿, 并可实现双定子多速马达不同工作方式间的切换。与滚柱式相比, 可实现更大的排量, 提高了比功率; 与连杆式相比, 减少了对定子曲线的磨损, 可实现间隙补偿且运转更平稳。在设计双定子多速马达时, 应首先满足内定子大圆弧处的密封。对于壳转型的双定子多速马达, 叶片不受离心惯性力的作用, 依然适用。通过对双作用双定子多速马达的实验, 验证了多速马达原理的正确性和马达设计的合理性。