串联式混合动力推土机节能率的解析分析

引用本文

张宝迪, 张欣, 席利贺, 刘林. 串联式混合动力推土机节能率的解析分析. 2015, 45(4): 1139-1147
ZHANG Bao-di, ZHANG Xin, XI Li-he, LIU Lin. Analysis of energy saving ratio in series hybrid electric bulldozer. Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1139-1147 复制到剪切板

Permissions

串联式混合动力推土机节能率的解析分析

张宝迪¹, 张欣¹, 席利贺¹, 刘林²

1.北京交通大学机械与电子控制工程学院,北京 100044

2.潍柴动力股份有限公司新能源技术中心,山东潍坊 261001

张欣(1959-),女,教授,博士生导师.研究方向:新能源汽车技术.E-mail:zhangxin@bjtu.edu.cn

作者简介:张宝迪(1988-),男,博士研究生.研究方向:车辆混合动力技术.E-mail:baodizhang@126.com

基金:“十二五”国家科技支撑计划项目(2011BAG04B02); 中央高校基本科研业务费专项项目(2013YJS076)

摘要

为探究混合动力推土机的节能效果、原因和潜力,推导出等效节油率与其影响因素的关系方程。将仿真与解析法相结合,分析了节能原因以及部件效率和循环工况对节能效果的影响,计算了等效节油率的极限值。结果表明:在典型循环工况下,节能主要源于电传动路径上较高的部件效率。在部件效率中,发动机效率对等效节油率的影响最显著。等效节油率随着推土阻力或行驶速度的提高而降低。不同优化措施下的节能极限可以利用解析式求得。

关键词: 机械设计; 混合动力系统; 推土机; 等效节油率; 等效能量转换效率; 解析法

中图分类号:TU623.5 文献标志码:A 文章编号:1671-5497(2015)04-1139-09

Analysis of energy saving ratio in series hybrid electric bulldozer

ZHANG Bao-di¹, ZHANG Xin¹, XI Li-he¹, LIU Lin²

1.School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044, China

2.New Energy Technology Center,Weichai Power Co., Ltd., Weifang 261001, China

Abstract

In order to explore the effect, the mechanism and the potential of energy saving in using series hybrid electric bulldozer, an analytical formula was deduced to present the relationship between the Equivalent Fuel Saving Ratio (EFSR) and the influencing factors. Combing simulation and analytical method, the mechanism of energy saving and the impacts of components' efficiencies and drive cycles on the energy saving effect were analyzed. The limit values of the EFSR were calculated. Results show that under typical drive cycle, the energy saving mainly originates from the higher components' efficiencies in the diesel-electric routine of the powertrain; the engine efficiency has the largest influence on the EFSR among all components' efficiencies. With the increase in bulldozing resistance or vehicle speed, the EFSR decreases. Moreover, the energy saving limit under various optimization measures can be calculated using the proposed analytical formula.

Keyword: mechanical design; hybrid electric powertrain; bulldozer; equivalent fuel saving ratio; equivalent energy conversion efficiency; analytical method

Show Figures

0 引言

采用混合动力系统的方式是降低能耗的主要方案之一, 其被广泛应用于汽车领域后又转向工程机械领域^{[1, 2, 3]}。对混合动力系统的结构、参数和控制策略开展研究, 实现节油的报道层出不穷^{[4, 5, 6]}, 然而大量研究主要关注于节油效果, 少有研究将电能的损耗计入节能效果评价, 尤其是探索节能的原因和潜力。

节能的根本是动力系统效率的提高。在阐明节油原因方面, 国内外有研究从不同角度分析动力系统效率展开^{[7, 8, 9, 10, 11]}, 这些研究主要采用粗略估算各部分能量损失, 或采用控制变量法变更参数对比油耗, 然而前者只能定性估测, 后者只能量化单一因素对节油率的影响, 都无法同时量化多个因素对节油率的影响。

近年来, Katrasnik等^{[12, 13, 14]}提出了一种独立的解析法, 该方法通过推导能量转换效率方程, 保留节油影响因素的全部信息, 揭示了不同混合动力系统的节油原因, 量化了拓扑结构等多个因素对油耗的影响。然而, Katrasnik的方法计算量大且极为复杂, Tobias等^[15]提出了简化的相似方法, 该方法对同一动力系统的效率采用驱动效率和制动效率两个指标进行评价, 这并不利于不同系统之间的对比, 故不便于分析节油的原因。此外, 在这些研究中均没有将电能的消耗计入, 对比等效油耗的节约(即节能), 也没有考虑对比系统质量或外形的不一致。目前, 国内仍鲜有采用解析法分析混合动力系统的节油或节能的原因。

本文将电能的损耗和整车质量或外形的改变考虑在内, 运用简化了的解析法推导出等效节油率的解析式, 建立两对比系统的整机模型并进行仿真, 结合仿真与解析式的计算, 对混合动力推土机的节能效果、原因和潜力进行了分析。

1 评价指标

为了使不同动力系统的油耗和效率可对比, 在混合动力系统中, 需要将电能存储单元在循环工况始末的能量变化考虑在内, 而且两系统的对比需要在相同工况下进行。本文分别以等效能量转换效率、等效传动系统效率和等效节油率作为动力系统效率、传动系统效率和节能率的评价指标。

文中变量和下标命名方法如表1所示。

表1 变量与下标 Table 1 Nomenclature and subscripts

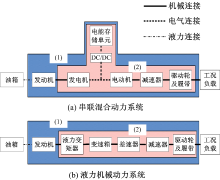
图1(a)(b)分别为推土机串联式混合动力系统和液力机械动力系统的结构示意图。图1中的框(1)范围内为动力系统, 框(2)范围内为传动系统。

	Figure Option View Download New Window
	图1 两种动力系统结构示意图Fig.1 Structure schematics of two types of powertrains

在混合动力系统中, 将工况始末电能存储单元的能量变化量换算到油箱, 如此可以将图1(a)(b)所示两种系统的工作过程都视为等效燃油的化学能转换为履带输出的机械能的过程, 该过程发生在图1中框(1)范围内。利用该过程的效率评价动力系统的整体效率, 定义为等效能量转换效率:

$\begin{matrix} \begin{matrix} η_{eq, ec} = E_{tr, out} / E_{eq, fu} (1) \\ 式中 : \\ E_{tr, out} = \int_{0}^{t_{cyc}} P_{tr, out} dt = \int_{0}^{t_{cyc}} F_{tr, out} v_{tr, out} dt (2) \\ E_{eq, fu} = V_{eq} ρ q_{l h v} = (V_{fu} + V_{eq, ess}) ρ q_{l h v} (3) \end{matrix} \end{matrix}$

在国家标准^[16]和SAE标准^[17]中, 计算等效油耗时部件的效率按估值代入, 而且不对电能存储单元的充、放电效率加以分别, 这将会对等效油耗的计算引入误差。为减小误差, 本文利用式(4)计算消耗电能的等效油耗量V_{eq, ess}。

V_{eq, ess}=

$\begin{matrix} \{\begin{matrix} Δ E_{ess} / (η_{fc} η_{g c} η_{ess, c h g} η_{dc, c h g} ρ q_{l h v}), SO C_{init} \geq SO C_{final} \\ Δ E_{ess} η_{ess, dis} η_{dc, dis} / (η_{fc} η_{gc} ρ q_{l h v}), SO C_{init} < SO C_{final} \end{matrix} \end{matrix}$ (4)

式中:Δ E_ess表示循环工况始末电能存储单元的电能改变量。

计算各部件的平均效率时, 可作如下假设:能量在两部件之间无论以机械、电力或液压的形式传递, 最终不在两部件之间的链接部分上积累, 即按照所有能量损失都由部件产生计算。则各部件的平均效率可按照式(5)(6)(7)计算:

$\begin{matrix} \begin{matrix} η_{m} = E_{m, out} / E_{m, in} = \int_{0}^{t_{cyc}} P_{m, out} (t) / \int_{0}^{t_{cyc}} P_{m, in} (t) (5) \\ E_{m, out} = E_{n, in} (6) \\ E_{m, in} = E_{l, out} (7) \end{matrix} \end{matrix}$

式中:下标m、n和l均为部件代号; 下标n表示当前能量流方向上m部件上游的部件; 下标l表示当前能量流方向上m部件下游的部件。

当式(5)用于能量传递部件的效率计算时, 部件效率为整个循环工况中, 当前部件输出给能量流下游部件的总能量与上游部件传递来的总能量之比。其中, 对于传递单向能量流的部件, 该效率为部件在整个循环工况的平均效率, 如下标m为“ gc” 、“ htc” 、“ ct” 或“ gb” 时; 对于传递双向能量流的部件, 分为驱动方向上的平均效率, 如下标m为“ mc, dr” 、“ fd, dr” 、“ tr, dr” 或“ dc, dis” 时, 和制动方向上的平均效率, 如下标m为“ mc, br” 、“ fd, br” 、“ tr, br” 或“ dc, chg” 时。

当式(5)用于能量源部件的效率计算时, 该效率为能量源输出的总能量与能量源消耗或获得的总化学能之比, 如m为“ fc” 、“ ess, dis” 或“ ess, chg” 。

在评价不同动力系统的经济性时, 经常需要分别对发动机和传动系统的效率进行对比, 为此引入等效传动系统效率的概念, 传动系统为从发动机功率输出轴端到履带功率输出端所构成的系统, 如图1(a)(b)中的框(2)范围内所示。定义等效传动系统效率为:

$\begin{matrix} η_{eq, trn} = E_{tr, out} / (η_{fc} E_{eq, fu}) (8) \end{matrix}$

2 解析式的推导与分析

若两对比推土机的质量和外形结构完全相同, 则在同一循环工况下动力系统需要输出的能量相等, 根据能量守恒存在如下关系式:

$\begin{matrix} \begin{matrix} V_{eq, h m} ρ q_{l h v} η_{eq, ec, h m} = V_{eq, h y} ρ q_{l h v} η_{eq, ec, h y} = \\ E_{tr, out} = const (9) \end{matrix} \end{matrix}$

式中:const表示定值。

然而, 多数情况下, 进行动力系统改造时, 整机质量和外形结构不可能完全相同, 若质量或外形结构发生改变, 在相同工况下两对比推土机的履带输出能量以式(10)表示:

$\begin{matrix} E_{tr, out, h y} = E_{tr, out, h m} (1 + γ_{total}) (10) \end{matrix}$

式中:γ _total表示动力系统输出能量改变的百分比。

则由式(8)(9)(10)可得等效节油率为:

$\begin{matrix} \begin{matrix} δ = 1 - \frac{V_{eq, h y}}{V_{eq, h m}} = 1 - \frac{η_{eq, ec, h m}}{η_{eq, ec, h y}} (1 + γ_{total}) = \\ 1 - \frac{η_{fc, h m} η_{eq, trn, h m}}{η_{fc, h y} η_{eq, trn, h y}} (1 + γ_{total}) (11) \end{matrix} \end{matrix}$

若η _{eq, ec, hy}=η _{eq, ec, hm}(1+∂ _{eq, ec}), η _{fc, hy}=η _{fc, hm}(1+∂ _fc), η _{eq, trn, hy}=η _{eq, trn, hm}(1+∂ _{eq, trn}), 则式(11)可化为:

$\begin{matrix} δ = 1 - \frac{1 + γ_{total}}{1 + \partial_{eq, ec}} = 1 - \frac{1 + γ_{total}}{(1 + \partial_{fc}) (1 + \partial_{eq, trn})} (12) \end{matrix}$

式(11)反映了等效节油率与等效能量转换效率、等效传动系统效率和输出能量改变的百分比的关系。式(12)反映了等效节油率与效率提高的百分比和输出能量改变的百分比的关系。

履带端输出能量可分为驱动能量和制动能量:

$\begin{matrix} E_{tr, out} = E_{dr} - E_{br} (13) \end{matrix}$

则由式(1)和(13)可知液力机械动力系统的等效能量转换效率可表示为:

$\begin{matrix} η_{eq, ec, h m} = \frac{(E_{dr, h m} - E_{br, h m})}{E_{dr, h m}} f_{h m} (14) \end{matrix}$

式中:f_hm为液力机械动力系统各部件在驱动方向上效率的乘积, 满足:

$\begin{matrix} f_{h m} = η_{fc} η_{h tc} η_{gb} η_{ct} η_{fd, dr} η_{tr, dr} (15) \end{matrix}$

在串联式混合动力系统中, 式(16)所示的功率平衡时刻存在, 电能存储单元的能量变化可表示为式(17)。

$\begin{matrix} \begin{matrix} P_{mc} = P_{ess} η_{dc} + P_{gc} (16) \\ Δ E_{ess} = E_{ess, dis} / η_{ess, dis} - E_{ess, c h g} η_{ess, c h g} (17) \end{matrix} \end{matrix}$

对式(16)两端积分, 可知在发电机、电动机和DC/DC交汇点处存在能量平衡, 即前、后功率链能量守恒。因此, 由式(1)(9)(13)(16)和(17)可导出串联式混合动力系统等效能量转换效率的解析式(18), 以及以液力机械动力系统为对照, 串联式混合动力系统的等效节油率的解析式(19)。

η _{eq, ec, hy}=

$\begin{matrix} \frac{(E_{dr, h y} - E_{br, h y}) f_{h y, e, dr}}{E_{dr, h y} - E_{br, h y} ξ f_{h y, b, al} + ψ (1 - f_{h y, ess, al}) f_{h y, b, dr}} \end{matrix}$ (18)

δ =

$\begin{matrix} {\{1 - \frac{f_{h m}}{f_{h y, e, dr}} (1 - γ_{total})\}}_{K_{1}} \end{matrix}$ +

$\begin{matrix} {\{\frac{f_{h m}}{f_{h y, e, dr} E_{dr, h m}} (1 - γ_{total}) E_{br, h m} ξ f_{h y, b, al}\}}_{K_{2}} \end{matrix}$ -

$\begin{matrix} {\{\frac{f_{h m}}{f_{h y, e, dr} E_{dr, h m}} (1 - γ_{total}) ψ (1 - f_{h y, ess, al}) f_{h y, b, dr}\}}_{K_{3}} \end{matrix}$ (19)

式(18)和(19)中:ξ 表示回收能量占制动能量的比例; ψ 表示换算到交汇点的充放电能量; f_{hy, e, dr}表示在“ 发动机-发电机-电动机-履带” 路径(即电传动路径)中各部件在驱动方向上的效率乘积; f_{hy, b, al}表示后功率链的全程效率; f_{hy, b, dr}表示后功率链在驱动方向上的效率; f_{hy, ess, al}表示交汇点到电能存储单元的全程效率。各变量的表达式如式(20)~(26)所示:

$\begin{matrix} \begin{matrix} ξ = E_{Rb, h y} / E_{br, h y} (20) \\ ψ = \{\begin{matrix} E_{ess, dis} / (η_{ess} η_{dc, c h g}), \\ E_{ess, c h g} / η_{dc, c h g}, \end{matrix} \begin{matrix} \end{matrix} \begin{matrix} SO C_{init} \geq SO C_{final} \\ SO C_{init} < SO C_{final} \end{matrix} (21) \\ f_{h y, e, dr} = η_{fc} η_{gc} η_{mc, dr} η_{fd, dr} η_{tr, dr} (22) \\ f_{h y, b, al} = η_{mc, dr} η_{mc, br} η_{fd, dr} η_{fd, br} η_{tr, dr} η_{tr, br} (23) \\ f_{h y, b, dr} = η_{mc, dr} η_{fd, dr} η_{tr, dr} (24) \\ f_{h y, ess, al} = η_{ess} η_{dc, dis} η_{dc, c h g} (25) \\ η_{ess} = η_{ess, dis} η_{ess, c h g} (26) \end{matrix} \end{matrix}$

在式(19)的等号右端, K₁项代表液力机械动力系统各部件效率的乘积与混合动力系统的电传动路径中各部件效率的乘积的对比; K₂项代表制动能量回收对等效节油率的贡献; K₃项代表与充放电过程中损耗能量相当的等效节油率。K₁、K₂和K₃三项共同构成了等效节油率。

式(14)(18)和(19)表示了等效能量转换效率和等效节油率与部件效率和输出能量的解析关系, 洞察了系统能量转换过程和节能原因, 解析式保留了影响节能的全部因素。

当忽略循环工况始末电能存储单元SOC的变化和整机质量或外形结构的差异时, 即认为Δ E_ess=0且γ _total=0时, 式(19)可经重排变型转化为文献[12]中所导方程, 从而间接验证了所导方程的正确性。

与文献[12]相比, 除研究对象不同外, 在解析式推导过程中, 本文在三个方面进行了优化:①计入了循环工况始末电能存储单元SOC的变化和因系统改造引起的整机质量或外形结构的差异; ②利用前后功率链交汇点处能量守恒的视角进行推导, 而非针对能量流进行计算; ③包含了对照系统中各部件的效率。其中:①可以使解析计算与实际的实验或仿真情况更吻合, 计算误差更小; ②简化了推导过程和解析式, 并使得式(19)仅含有单一部件的输出或输入能量总量的子项, 这比子项为同一部件不同流向的能量在实际操作中更易测量和计算; ③更加明晰了不同系统中各部件的效率对比。

3 实例计算分析

为了利用解析式进行分析, 需要首先通过实验或仿真获取两对比系统中各部件的瞬时工作点数据, 并经计算得到解析式中的各子项。本文利用仿真获取各部件的瞬时工作点数据。

3.1 仿真对比分析

为了增加两类推土机的可对比性, 同时考虑到模型的简化, 在不影响燃油经济性分析的基础上, 本文建模仿真时作如下假设:①忽略各部件瞬态效率和稳态效率的偏差, 即不考虑瞬态过程; ②仿真开始时发动机冷却液温度为90℃, 即暖机过程结束; ③两类系统除传动系统外其他零部件完全相同; ④两类系统使用相同的发动机。

根据动力系统结构(见图1)对ADVISOR进行二次开发, 建立混合动力推土机模型和液力机械推土机模型, 建模过程详见文献[18]。

在模型中, 动力学模块需要根据推土机行驶动力学方程(27)进行修改, 履带行走机构模型可以根据履带车辆行驶运动学方程(28)和滑转率经验方程(29)对原轮胎模型进行修改而得。

$\begin{matrix} F_{tr, out} = F_{r} + F_{i} + F_{j} + F_{A} + F_{X} (27) \end{matrix}$

式中:F_r为滚动阻力; F_i为坡道阻力; F_j为惯性阻力; F_A为风阻; F_X为推土阻力。

$\begin{matrix} v_{ac} = v_{t h} (1 - s) = rω (1 - s) (28) \end{matrix}$

式中:v_ac为实际行驶速度; v_th为理论行驶速度; s为滑转率; r为驱动轮动力半径; ω 为驱动轮旋转角速度。

$\begin{matrix} s = a (\frac{F_{ef}}{mg}) + b {(\frac{F_{ef}}{mg})}^{n} (29) \end{matrix}$

式中:F_ef为有效牵引力; a、b和n为与行走机构类型以及地面有关的常数, 可采用同级别机型的滑转率实验数据确定。

发动机、发电机、电动机、超级电容、变速箱和液力变矩器等部件模块均可利用ADVISOR模型库中的原有模型。该模型是采用实验建模与理论建模相结合的方法, 利用查表法查取各部件实验特性曲线或特性Map数据, 考虑温度、转动惯量等影响因素后建立数学模型所得。

混合动力系统采用发动机开关恒温控制策略:发动机打开时, 始终将发动机和发电机控制于整个发动机和发电机组最优效率点(1336 r/min, 1130 N· m)工作, 超级电容进行功率平衡。当超级电容SOC大于最高限值0.9时发动机关闭由超级电容单独驱动, 直到SOC小于最低限值0.6时发动机打开单独驱动并给超级电容充电, 需求功率超过发动机最大输出功率时两者共同驱动。

液力机械系统采用基于负荷的换档策略:根据发动机Map设定升档和降档的曲线, 在特定转速高于设定的负荷度时升档, 低于设定的负荷度时降档。

将某公司提供的典型循环工况数据、整机参数和各部件效率Map输入模型。两系统主要参数如表2和表3所示, 典型循环工况谱如图2所示。

表2 液力机械推土机主要参数 Table 2 Main parameters of hydro-mechanical bulldozer

表3 混合动力推土机主要参数 Table 3 Main parameters of series hybrid electric bulldozer

	Figure Option View Download New Window
	图2 典型循环工况下的速度和有效牵引力Fig.2 Effective traction and speed in typical drive cycle

由仿真可得两系统的油耗和各部件瞬时工作点的数据, 将各时刻的离散数据带入评价指标的定义式(1)(5)和(8)可求得等效传动系统效率、等效能量转换效率和各部件的平均效率。典型循环工况下, 两推土机的履带输出总能量、等效油耗和部件平均效率的对比, 如表4所示。

将仿真所得的需求能量和各部件的平均效率带入解析式(19), 所求得的等效节油率与表4中仿真所得等效油耗的对比相一致, 表明解析式推导无误。

表4 两种系统等效油耗和效率的对比 Table 4 Comparisons of equivalent fuel consumption and efficiency between two kinds of powertrains

项目	液力机械推土机(hm)	混合动力推土机(hy)	$\begin{matrix} \frac{(hy - hm)}{hm} \end{matrix}$ × 100%
整机质量/t	28.05	27.52	-1.95%
等效油耗/L	0.42	0.37	-12.22%
输出总能量/MJ	4.34	4.30	-0.81%
部件平均效率/%	η _fc=42.88	η _fc=44.74	4.32%
	η _tr=90.58	η _tr=90.27	-0.34%
	η _htc=80.76	η _gc=92.99	-
	η _gb=95.99	η _mc=90.60	-
	-	η _ess=94.49	-
等效能量转换效率/%	28.32	32.00	13.00%
等效传动系统效率/%	66.04	71.53	8.32%

表4 两种系统等效油耗和效率的对比 Table 4 Comparisons of equivalent fuel consumption and efficiency between two kinds of powertrains

由表4可见, 与传统推土机对比, 混合动力推土机的整机质量降低了1.95%, 这是因为本研发实例在由原型机改造为混合动力推土机的过程中, 液力变矩器、变速箱、传动轴和转向离合器等机械传动部件被替换。输出的总能量降低了0.81%, 其原因由车辆动力学方程可知, 在相同循环工况下, 履带输出总能量受迎风面积和质量的影响, 因外形结构未发生改变, 输出总能量的降低由整机质量的降低所引起。履带系统的平均效率η _tr降低了0.34%, 由文献[19]可知, 滑转率受整机质量、履带结构和土壤参数的影响, 因混合动力系统只有整机质量降低, 而整机质量的降低会导致相同有效牵引力下滑转率的提高, 所以履带系统平均效率降低。表4还显示, 混合动力推土机中发动机的平均效率η _fc提高了4.32%, 这是因为在串联式混合动力系统中前后功率链解耦, 发动机的工作点不直接受工况影响, 发动机的工作可以被控制在高效率区, 而液力机械动力系统则不然。等效传动系统效率提高了8.32%, 原因是在传动系统的对比中, 虽然混合动力推土机的履带效率η _tr降低了, 但原型机中的液力变矩器的平均效率η _htc仅有80.76%, 而混合动力系统中各部件平均效率整体较高。传动系统和发动机的效率提高综合反映为等效能量转换效率提高了13.00%。等效能量转换效率的提高和输出总能量的下降共同反映为等效油耗下降12.22%, 其关系由式(12)可知。

由上述分析可知, 所有提高节油率的技术本质上均是提高动力系统的等效能量转换效率或降低终端输出能量的技术。

3.2 解析分析

3.2.1 部件效率对节能的影响

采用不同效率水平的部件或不同的匹配方法、控制策略, 都会导致特定工况下同种部件表现出不同的平均效率, 最终造成了同类动力系统表现出不同的节能效果。

为研究部件效率对等效节油率的影响, 基于前文中仿真结果(见表4), 各部件的平均效率在当前技术水平的范围内取值代入式(19)计算, 结果如图3所示。据大量文献[3, 6, 10, 12]显示, 混合动力系统中, 发动机、发电机、电动机、超级电容的平均效率范围分别为40%~50%、88%~96%、85%~96%、90%~98%。

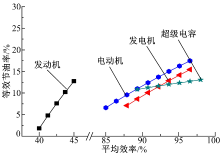	Figure Option View Download New Window
	图3 部件平均效率对等效节油率的影响Fig.3 Effects of average efficiency of each component on equivalent fuel saving ratio

选取发动机和发电机效率范围的原则为:将发动机和发电机控制于两者协同工作的效率最优点, 选取各文献中发动机和发电机的最高效率。而电动机和超级电容的效率范围为直接选取文献中同类部件的平均效率范围。

由图3可见, 各部件平均效率的提高均引起等效节油率的提高, 而提高的程度与范围不同。经计算, 图中发动机所对应的曲线斜率为2.18, 发电机为0.96, 电动机为0.94, 超级电容为0.27。可知, 发动机效率的提高对等效节油率的提高影响最为显著, 超级电容效率的提高对等效节油率的提高影响最不明显, 发电机和电动机的作用适中且较为接近。因此, 在考虑总成本时, 应优先选择较高效率水平的发动机。

另外, 如图3所示, 单个部件平均效率的差异足以引起等效节油率的显著差别, 可知多个部件平均效率差异的综合作用对等效节油率的影响更大, 因此动力系统并非进行混合化或采用高水平的匹配方法和控制策略就一定能够节能或节能更高, 还应足够重视不同水平的部件效率和不同工况下的部件效率。

3.2.2 循环工况对节能的影响

在不同的循环工况下, 同一动力系统会表现出不同的节能效果。为研究不同循环工况下节能效果及成因, 需要首先构建循环工况。

构建循环工况需要结合推土机实际工作情况, 并能够通过在所构建循环工况下的计算, 分别反映出工况中不同要素(行驶速度或有效牵引力)的变化对节能效果的影响。由于本文中两对比推土机的最大有效牵引力的设计目标均为170 kN, 最高速度的设计目标均为11 km/h, 而在典型循环工况(见图2)中, 最高速度约7 km/h, 积土时最大有效牵引力高达167 kN, 运土时平均有效牵引力高达130 kN, 因此该循环工况下两推土机为中速高负荷运行。

采用类似文献[12]和[20]中的方法, 以典型循环工况为基准, 分别对典型循环工况中的有效牵引力和速度按比例进行缩放。将典型循环工况中各时刻下的有效牵引力和速度分别乘以比例系数k_F和k_ν, 构建T₁和T₂两组循环工况。

T₁组和T₂组中各包含5个循环工况, 比例系数k_F和k_v的选取如表5所示。T₂组循环工况中, 各时刻速度与典型循环工况相同(k_v=1), 有效牵引力分别乘以0.4、0.5、0.6、0.8和1, 构建该组工况意在研究相同速度下, 不同负荷对等效节油率的影响; T₂组循环工况中, 各时刻有效牵引力与典型循环工况相同(k_F=1), 速度分别乘以0.4、0.5、0.6、0.8和1, 构建该组工况意在研究相同有效牵引力下, 不同速度对等效节油率的影响。

表5 比例系数k_F和k_ν的值 Table 5 Values of k_F and k_v as scaling factor

图4(a)(b)分别表示了在T₁组和T₂组工况下的等效节油率δ 及式(19)等号右端三项(K₁, K₂和K₃)的值。

由图4(a)(b)可见, 等效节油率δ 总体上随着k_F或k_v的增大而减小, 这表明等效节油率具有随着循环工况中推土阻力或速度的提高而降低的趋势。但需要说明的是:在图4(a)中, k_F小于0.6时等效节油率略微上升, 该部分与总体降低的趋势不一致是由于在该部分中原型机的运行档位和各档位上的运行时间发生了改变, 这导致了液力变矩器的效率因换档而下降, 从而相对比之下等效节油率略微上升, 而在k_F大于0.6之后, 运行档位不发生改变也能够跟随行驶工况, 这种档位不一致的影响因素就不存在了。因此, 忽略这种档位不一致的影响时, 纵观图4(a)中k_F变化曲线, 可认为等效节油率呈现下降的总体趋势。因仿真中原型机采用ADVISOR内基于负荷的换档策略, 当速度改变而负荷不变时, 档位状态可以不发生改变, 故此时不受上述因素影响, 如图4(b)所示, 等效节油率始终呈下降趋势。

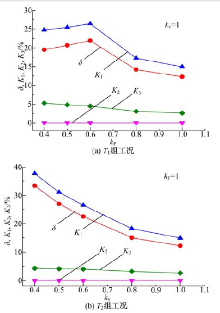	Figure Option View Download New Window
	图4 两组循环工况下的等效节油率及其组成参数Fig.4 Equivalent fuel saving ratio and its contribution factors under two groups of test cycles

在两组循环工况中, 等效节油率δ 的曲线始终低于K₁曲线, 并且与K₁曲线的趋势保持一致。由式(19)可知δ =K₁+K₂-K₃, 因此, δ 与K₁曲线的关系表明等效节油率主要是由混合动力系统中电传动路径上部件效率的乘积高于液力机械动力系统中部件效率的乘积所产生。

K₂几乎为0, 这表明在两组循环工况下没有可以回收的能量, 故对提高等效节油率无贡献。

K₃较小且随着k_F或k_v的提高而略微降低。这是因为超级电容充放电效率高, 电能存储单元充放电路径上因能量损耗所“ 丧失” 的等效节油率较小。当需求功率提高时, 发电机所发出的电能主要用来满足后功率链的需求, 充放电的能量损耗相应减少, 故略微降低。

3.2.3 节能的极限

为了把握某项技术条件下所能达到的节能极限, 可以利用解析式(19)计算等效节油率的极限值。

表6为3种极限条件及相应条件下等效节油率的极限值。其中, A情况表示发动机和发电机在两者协同工作的最优效率点运行, 且电能存储单元的充放电损耗为零(实际上能量管理策略无论如何优化也不可能达到此状态, 但可以以此作为优化能量管理策略的极限), 此极限条件下的等效节油率记作δ _A, 即在不改变混合动力推土机的部件匹配、外形结构、整机质量和行驶工况的情况下, 仅通过优化能量管理策略所能达到的等效节油率的极限; B情况表示除满足A情况的极限条件外, 电动机始终工作在其最高效率点(实际上除电动机始终以特定的转速和转矩工作外不可能实现, 但可以以此作为优化后功率链匹配的极限), 此极限条件下的等效节油率记作δ _B, 即在不改变混合动力推土机前功率链的匹配、外形结构、整机质量和行驶工况时, 通过优化能量管理策略和后功率链的匹配所能达到的等效节油率的极限; C情况表示发动机、发电机和电动机均始终以最高效率点工作, 且电能存储单元的充放电损耗为零(实际上任何技术措施也不可能达到此状态, 但可以以此作为所有技术优化的极限), 此极限条件下的等效节油率记作δ _C, 即在不改变混合动力推土机的外形结构、整机质量和行驶工况时, 在当前部件效率水平下, 利用所有技术措施所能达到的等效节油率的极限。

表6 三种极限条件下的等效节油率 Table 6 Limit values of equivalent fuel saving ratio under three kinds of limiting conditions

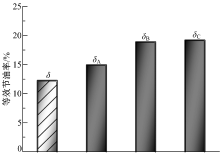
基于前文中两对比推土机在典型循环工况下的仿真结果, 计算上述3种极限条件下的等效节油率结果如图5所示。

由图5可见, 在典型循环工况下, 等效节油率为12.22%, 3种极限条件的等效节油率分别为14.93%、18.86%和19.15%。由此可知, 在不改变混合动力推土机的部件匹配、外形结构、整机质量和行驶工况时, 本文所采用的能量管理策略水平已经较高, 继续优化能量管理策略可以提高的等效节油率不足3%。而其他条件不变, 通过优化能量管理策略与优化后功率链传动比相结合可以提高的等效节油率不超过7%。在不更换更高效率水平的部件、不改变行驶工况且不改变质量或外形结构时, 采用任何技术也不能使等效节油率超过19.15%。

	Figure Option View Download New Window
	图5 典型循环工况下的等效节油率与极限值Fig.5 Equivalent fuel saving and its limit values in typical drive cycle

4 结束语

利用解析法推导出等效节油率的解析式, 将建模仿真与解析法相结合, 分析了不同条件下混合动力推土机的节能效果及原因, 计算了等效节油率的极限值。结果表明:在典型循环工况下, 混合动力推土机的节能主要源于电传动路径上较高的部件效率, 其中发动机的效率对节能效果影响最显著。循环工况改变时, 等效节油率随着推土阻力或行驶速度的提高而降低。利用所导解析式可以求得采用不同措施优化节能的极限。本文回答了混合动力推土机“ 能否节能, 为何节能, 节在何处以及有多大节能潜力” 的问题。所导解析式可以应用于相同系统的其他车辆, 所利用的解析法可以推广到其他拓扑结构的车辆。利用解析法衡量节能的效果、成因、潜力和方向可用于选择节能技术和评估混合动力化的可行性等方面。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	欧阳明高. 我国节能与新能源汽车发展战略与对策[J]. 汽车工程, 2006, 28(4): 317-318. Ouyang Ming-gao. Development strategy and countermeasures of the energy saving and the vehicle with new energy in our country[J]. Automobile Engineering, 2006, 28(4): 317-318. [本文引用:1]
[2]	刘刚, 宋德朝, 陈海明, 等. 并联混合动力挖掘机系统建模及控制策略仿真[J]. 同济大学学报: 自然科学版, 2010, 38(7): 1079-1084. Liu Gang, Song De-chao, Chen Hai-ming, et al. Modeling and control strategy of parallel hybrid system in hydraulic excavator[J]. Journal of Tongji University (Natural Science), 2010, 38(7): 1079-1084. [本文引用:1]
[3]	杨蓉, 楼狄明, 庞然, 等. 串联式混合动力推土机系统建模及性能仿真[J]. 中国工程机械学报, 2012, 10(3): 280-285. Yang Rong, Lou Di-ming, Pang Ran, et al. System modeling and performance simulation on series hybrid bulldozers[J]. Chinese Journal of Construction Machinery, 2012, 10(3): 280-285. [本文引用:1]
[4]	王庆年, 金启前, 初亮, 等. 传动系参数和控制参数对并联混合动力轿车性能的影响[J]. 吉林大学学报: 工学版, 2005, 35(3): 243-247. Wang Qing-nian, Jin Qi-qian, Chu Liang, et al. Effects of power train parameters and control parameters on performance of parallel hybrid electric car[J]. Journal of Jilin University (Engineering and Technology Edition), 2005, 35(3): 243-247. [本文引用:1]
[5]	王庆年, 曾小华, 王伟华. 混合动力技术在军用汽车上的应用[J]. 吉林大学学报: 工学版, 2003, 33(1): 39-41. Wang Qing-nian, Zeng Xiao- hua, Wang Wei- hua. Application of the hybrid power on military vehicle[J]. Journal of Jilin University (Engineering and Technology Edition), 2003, 33(1): 39-41. [本文引用:1]
[6]	曾小华, 巴特, 田浩, 等. 混联混合动力客车动力系统参数匹配[J]. 吉林大学学报: 工学版, 2013, 13(2): 278-284. Zeng Xiao-hua, Ba Te, Tian Hao, et al. Powertrain parameter matching of series-parallel hybrid electric bus[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 13(2): 278-284. [本文引用:1]
[7]	An F, Santini D. Assessing tank-to-wheel efficiency of advanced technology vehicles[C]∥SAE Paper, 2003-01-0412, 2003. [本文引用:1]
[8]	Huang W D, Zhang Y H P. Energy efficiency analysis: biomass-to-wheel efficiency related with biofuels production, fuel distribution, powertrain systems[J]. PLoS ONE, 2011, 6(7), e22113: 1-10. [本文引用:1]
[9]	刘明辉, 赵子亮, 李骏. 混合动力汽车节油机理研究[J]. 汽车技术, 2005(5): 11-13. Liu Ming-hui, Zhao Zi-liang, Li Jun. A study on fuel saving mechanisms for hybrid electric vehicles[J]. Automobile Technology, 2005(5): 11-13. [本文引用:1]
[10]	王成, 郭淑英, 刘凌. 串联式混合动力系统在公交客车中的开发与应用[J]. 机械工程学报, 2009, 45(2): 18-24. Wang Cheng, Guo Shu-ying, Liu Ling. Development and application of serial hybrid electric powertrain system in the bus[J]. Journal of Mechanical Engineering, 2009, 45(2): 18-24. [本文引用:1]
[11]	魏跃远, 林程, 林逸, 等. 混合动力汽车系统效率的影响因素[J]. 吉林大学学报: 工学版, 2006, 36(1): 21-24. Wei Yue-yuan, Lin Cheng, Lin Yi, et al. Factors influencing hybrid electric vehicle system efficiency[J]. Journal of Jilin University (Engineering and Technology Edition), 2006, 36(1): 21-24. [本文引用:1]
[12]	Katrasnik T, Trenc F, Opresnik S R. Analysis of energy conversion efficiency in parallel and series hybrid powertrains[J]. IEEE Transactions on Vehicular Technology, 2007, 56(6): 3649-3659. [本文引用:1]
[13]	Katrasnik T. Energy conversion phenomena in plug-in hybrid-electric vehicles[J]. Energy Conversion Management, 2011, 52(7): 2637-2650. [本文引用:1]
[14]	Katrasnik T. Analytical framework for analyzing the energy conversion efficiency of different hybrid electric vehicle topologies[J]. Energy Conversion Management, 2009, 50(8): 1924-1938. [本文引用:1]
[15]	Tobias Ott, Florian Zurbriggen, Christopher Onder, et al. Cycle-averaged efficiency of hybrid electric vehicles[J]. Journal of Automobile Engineering, 2013, 227(1): 78-86. [本文引用:1]
[16]	全国汽车标准化技术委员会. GB/T19754-2005重型混合动力电动汽车能量消耗量试验方法[S]. 2005. [本文引用:1]
[17]	SAE J2711. Recommended practice for measuring fuel economy and emissions of hybrid-electric and conventional heavy-duty vehicles[S]. 2002. [本文引用:1]
[18]	Zhang Bao-di, Zhang Xin, Xi Li-he, et al. Development of simulation model for series hybrid electric crawler bulldozer (SHECB) based on ADVISOR[J]. Advanced Materials Research, 2013, 732: 337-343. [本文引用:1]
[19]	蔡应强. 影响推土机滑转率的因素[J]. 集美大学学报: 自然科学版, 2008, 13(1): 67-71. Cai Ying-qiang. Influencing factors of the slip rate of bulldozer[J]. Journal of Jimei University (Natural Science), 2008, 13(1): 67-71. [本文引用:1]
[20]	Katrasnik T. Hybridization of powertrain and downsizing of IC engine-analysis and parametric study-part2[J]. Energy Conversion Management, 2007, 48(5): 1424-1434. [本文引用:1]

2006

0.0

... 0 引言采用混合动力系统的方式是降低能耗的主要方案之一,其被广泛应用于汽车领域后又转向工程机械领域^[1,2,3] ...

2010

0.0

... 0 引言采用混合动力系统的方式是降低能耗的主要方案之一,其被广泛应用于汽车领域后又转向工程机械领域^[1,2,3] ...

2012

0.0

... 0 引言采用混合动力系统的方式是降低能耗的主要方案之一,其被广泛应用于汽车领域后又转向工程机械领域^[1,2,3] ...

2005

0.0

. 2005, 35(3):243-247

Effects of power train parameters and control parameters on performance of parallel hybrid electric car

传动系参数和控制参数对并联混合动力轿车性能的影响

Wang Qing-nian , Jin Qi-qian , Chu Liang

王庆年, 金启前, 初亮

以Matlab/Simulink环境下的ADVISOR软件为仿真平台，通过二次开发和建模，研究了并联混合动力轿车传动系参数和控制参数对整车动力性和经济性的影响，并在混合动力试验台架上进行了验证。结果表明：传动系参数对整车动力性和经济性有着决定性的影响，参数混合度R取值越大，经济性越好；控制参数中的电量控制参数对整车经济性的影响相对显著；特定试验工况循环下，只要电池系统匹配合理，SOC值就能够维持在一定的水平。

... 对混合动力系统的结构、参数和控制策略开展研究,实现节油的报道层出不穷^[4,5,6],然而大量研究主要关注于节油效果,少有研究将电能的损耗计入节能效果评价,尤其是探索节能的原因和潜力 ...

2003

0.0

2013

0.0

2003

0.0

... 在阐明节油原因方面,国内外有研究从不同角度分析动力系统效率展开^{[7,8,9,10,11]},这些研究主要采用粗略估算各部分能量损失,或采用控制变量法变更参数对比油耗,然而前者只能定性估测,后者只能量化单一因素对节油率的影响,都无法同时量化多个因素对节油率的影响 ...

2011

0.0

2009

0.0

2006

0.0

2007

0.0

... 近年来,Katrasnik等^[12,13,14]提出了一种独立的解析法,该方法通过推导能量转换效率方程,保留节油影响因素的全部信息,揭示了不同混合动力系统的节油原因,量化了拓扑结构等多个因素对油耗的影响 ...

2011

0.0

2009

0.0

2013

0.0

... 然而,Katrasnik的方法计算量大且极为复杂,Tobias等^[15]提出了简化的相似方法,该方法对同一动力系统的效率采用驱动效率和制动效率两个指标进行评价,这并不利于不同系统之间的对比,故不便于分析节油的原因 ...

2005

0.0

... 在国家标准^[16]和SAE标准^[17]中,计算等效油耗时部件的效率按估值代入,而且不对电能存储单元的充、放电效率加以分别,这将会对等效油耗的计算引入误差 ...

2002

0.0

2013

0.0

2008

0.0

2007

0.0