作者简介:吴越(1984-),男,讲师,博士.研究方向:微小机械与精密机械,压电驱动与换能.E-mail:wuyues@163.com
为了解决压电悬臂梁发电装置俘获低频振动时,结构共振频率带宽小不能完全发挥其发电能力的问题,对压电悬臂梁进行模态分析,结合汽车轮胎压力检测系统中自供电的要求与悬臂梁式发电装置振动模态的特点,提出利用弯曲振动模态和扭转振动模态构成压电悬臂梁发电装置,利用分布式的质量块布置方式实现弯曲模态与扭转模态的解耦,并使用有限元方法对其进行仿真计算。仿真结果表明:在一阶弯曲模态固有频率为12.6 Hz不变的条件下,通过调整质量块分布位置,将弯曲模态的固有频率降低到17.2 Hz。对改进的压电悬臂梁发电装置进行试验,结果表明其发电能力是同条件下传统的集中质量块式悬臂梁发电装置的1.4倍。
The power generation capacity of piezoelectric cantilever beam generator can not fully play due to that its resonance frequency bandwidth is small when capture low-frequency variation. To overcome this problem, modal analysis of the piezoelectric cantilever beam was carried out. Combining with the requirement of self-power of automobile tire pressure detection system and the characteristics of the vibration mode of the cantilever type power device, a scheme was proposed. In this scheme, the bending and torsion vibration modes were utilized to constitute the piezoelectric cantilever generator; the bending mode and torsion mode were decoupled by the distributed mass block arrangement. Finite element simulation was carried out. The simulation results show that, under the condition that the first bending mode frequency is 12.6 Hz, by adjusting the mass block distribution, the natural frequency of the flexural mode can be reduced to 17.2 Hz. Under the same condition, the power generation capacity of the improved piezoelectric cantilever beam generator is about 1.4 times of that of the traditional centralized mass piezoelectric cantilever beam generator.
近年来压电发电作为一种新型的能量俘获方式, 已经成为微小型发电装置的研究热点[1, 2], 利用收集流体运动[3]、噪声振动及环境振动中的能源[4, 5]构成的压电发电装置具有结构简单、体积小、寿命长、无电磁干扰等优点[6, 7, 8, 9, 10], 已经在不同领域替代传统的电池供电方式[2, 11], 包括为汽车轮胎压力监视系统(Tire pressure monitoring system, TPMS)供电[12, 13]。在以往的研究中发现, 车轮内部的复合振动频率较低, 一般在10~20 Hz之间[14], 要在该范围内构成有效的发电装置, 一般希望所构成的振动能量俘获装置工作在共振状态, 同时具有较高的发电电压, 即悬臂梁发生大的变形, 且系统带宽较大, 能在不同振动频率下获得更高的总发电量。以往的研究中有采用多悬臂梁方式增加系统带宽的[15], 但存在结构相对复杂、不易小型化的缺点; 也有研究者提出了利用悬臂梁的两阶沿悬臂梁长度方向弯曲振动的多模态复合发电装置, 但不同弯曲模态相互耦合, 不能进行独立调整, 该方式的适用频率范围受到制约[16, 17]。为了解决该问题, 本文提出通过机械结构设计, 将扭转模态与弯曲模态解耦, 在低频区间内布置多阶共振频率, 以形成宽频发电装置, 提高振动利用率。
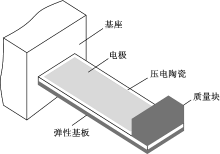
图1所示为典型的集中质量式压电悬臂梁发电装置简图。由于其结构简单、工艺性好且便于分析而被广泛用于传感器、能量俘获装置及自供电装置中。该装置包括压电双晶片、金属弹性基板及质量块构成的压电悬臂梁发电机构和基座。当基座发生振动时, 质量块在惯性作用下带动压电悬臂梁发生振动, 引起压电材料产生应变, 在压电材料正压电效用的作用下, 将该应变转化成压电材料两电极间的电压, 从而实现了将基座的振动转化为电能的俘能效果。
模态响应分析一般用于研究结构的固有振动特性, 通过有限元方法可以得到各阶模态的固有频率及其变形方式, 而其变形的大小直接影响其表面产生电荷量的多少, 变形方式影响电荷的正负性质。模态响应分析的一般步骤为:定义材料属性、选择单元类型、建立分析模型、网格划分、施加约束和载荷、定义分析参数、仿真计算、结果读取和处理。模态分析的前处理过程中, 忽略压电陶瓷与基板、压电陶瓷与质量块之间的粘结层, 通过布尔操作进行实体粘接, 六面体网格划分为1 mm大小, 因压电陶瓷上表面覆盖电极的连续性和下表面粘接层的导通性, 将压电陶瓷上表面各节点电压值进行耦合处理, 使其各节点电压值相同, 同时下表面各节点电压设为零。约束条件选择在压电悬臂梁无质量块一端进行固定支撑约束, 即固定区域各节点的自由度为0, 其他位置外加负载为0。分析模态阶数为6, 频率响应范围为0~3000 Hz。压电悬臂梁基板和压电晶片的材料属性如表1所示。常用压电材料包括软性材料(PZT5)和硬性材料(PZT8)等类型, 此处选择压电常数d31更大的PZT5材料, 参数如下:
弹性劲度系数矩阵:
弹性柔顺系数矩阵:
压电应力常数矩阵:
压电应变常数矩阵:
介电常数矩阵:
悬臂梁结构中基板尺寸为40 mm× 14 mm× 0.3 mm, 陶瓷尺寸为30 mm× 14 mm× 0.25 mm, 质量块尺寸为2 mm× 14 mm× 2 mm。
| 表1 压电悬臂梁基板和压电晶片材料属性 Table 1 Material properties of elastic substrate and piezoelectric wafer |
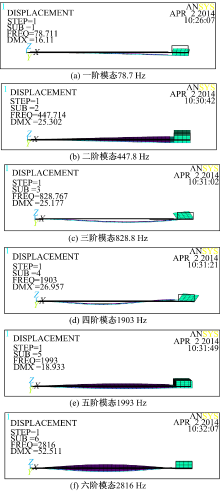
使用ANSYS软件对上述传统的集中质量压电悬臂梁振动发电装置进行仿真, 获得其前6阶的模态, 如图2所示。一、三、四阶模态为沿着悬臂梁结构长度方向的弯曲模态, 而二阶模态表现为质量块沿着悬臂梁长度方向中心轴线的扭转模态, 五、六阶模态为弯扭复合模态。可见前三阶模态的谐振频率较低, 且其运动方式更有利于振动能量的收集, 符合在TPMS中转换振动能量的要求, 但三阶频率与一阶频率难以同时落在TPMS所需的10~20 Hz区间, 因此选择一阶弯曲模态和二阶扭转模态作为本发电装置的振动形式。
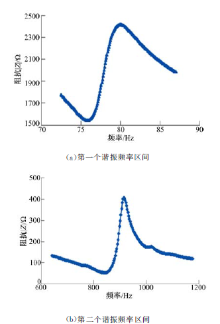
为了验证仿真所得到的压电悬臂梁各阶固有频率的准确性, 试制了如图1所示的集中质量式压电悬臂梁, 利用阻抗分析仪对其进行固有频率测试, 包括电压与电流的相位和阻抗值随频率的变化关系, 二者都可以判断系统的谐振频率, 本文选择阻抗最小处作为系统的谐振频率, 阻抗分析曲线如图3所示, 通过试验结果可知, 压电悬臂梁的一阶和三阶弯曲模态特征频率与实测值接近, 而二阶扭转模态特征频率并未在阻抗特性中出现。
通过模态仿真分析结果可知, 系统的二阶扭转振动是沿着压电悬臂梁长度方向中轴线的旋转运动, 利用扭转模态发电时, 在压电悬臂梁上不同区域的压电陶瓷受到的应力方向不同, 如图2(b)所示, 沿着悬臂梁长度方向中轴线分开, 当一侧的分布质量块向下运动时, 另一侧的分布质量块向上运动, 向下运动一侧的压电陶瓷受到沿表面方向的拉应力, 而向上运动一侧的压电陶瓷受到沿表面方向的压应力, 两区域内的压电陶瓷的极化方向相同, 其受力后产生的电场方向相反, 可见在该模态下压电陶瓷发出电量大部分会被抵消, 因此通过电学测试设备无法有效地测试该模态特征频率。
通过对二阶模态的变形特性分析, 为了同时利用一阶弯曲模态和二阶扭转模态进行能量转换, 本试验中所采用压电陶瓷的电极在悬臂长度方向的轴线处进行分割, 两部分分别进行电量收集, 且分割后的电极可以直接接入阻抗分析仪对其前三阶固有频率进行测试。
压电悬臂梁质量为m, 在其自由端的集中质量为M, 则发电装置的一阶弯曲振动可等效为如图4所示的动力学系统, 其动力学方程为
式中:等效弹簧刚度keq=(3EI)/l3; 等效集中质量meq=M+0.23m; l为悬臂梁长度; E为压电悬臂梁的等效杨氏模量; I为截面对中性轴的惯性矩。
系统无阻尼固有频率为
前文所得到的压电发电装置的系统前2阶频率过高, 为了降低压电悬臂梁发电装置的固有频率, 减小悬臂梁的厚度尺寸, 同时增加集中质量, 当陶瓷基板厚度为0.1 mm、压电陶瓷厚度为0.1 mm、质量块体积增加一倍时, 系统的一阶固有频率降低到12.10 Hz。系统共振的频宽为
式中:ζ 为系统阻尼系数; ω n为系统固有频率。
根据仿真结果可见, 其频宽约为1.5 Hz, 此时系统在10~15 Hz频率区间内可能有较好的发电效果, 而在15~20 Hz区间发电效果会明显下降。通过调整等效刚度与质量将系统的基频降低后, 频宽同时减小, 而通过增加系统阻尼增加带宽会直接影响输出的最大振幅, 用一阶固有频率无法实现低频、高带宽的发电要求。为了提高发电性能, 通过结构设计使换能机构的二阶扭转模态的固有频率处于15~20 Hz区间内。以往直接通过调节系统刚度与质量的方法实现降低频率的方案遇到了问题, 当二阶频率下降到20 Hz以下时, 其一阶振动频率已经降低到10 Hz以下, 由于该参数会同时影响弯曲模态和扭转模态固有频率, 二者相互耦合, 因此上述动力学参数的调整无法实现两阶模态的有效设计。
影响一阶弯曲模态的关键参数是压电悬臂梁的刚度、质量及质心与支撑件的距离, 而影响扭转模态的关键参数是扭转刚度、质量及其距离扭转中心的距离(即转动惯量)。在不改变质量与弹性件尺寸, 保证影响一阶弯曲模态动力学系统参数不变的情况下, 通过质量的布置方式改变转动惯量即可实现弯曲模态与扭转模态的解耦, 实现扭转模态与弯曲模态固有频率的独立调整。如图5所示, 在集中质量压电悬臂梁基础上, 不改变其总体质心位置, 通过调整两个质量块在悬臂梁宽度方向间距的方式, 实现转动惯量调整的分布式质量压电悬臂梁发电结构。
通过调整两分布质量间的距离对转动惯量进行调节, 选择两质量块间距为4、8、12 mm, 通过仿真可得到如表2所示的结果。
| 表2 压电悬臂梁各阶模态固有频率 Table 2 Natural frequency of piezoelectric cantilever |
对比仿真结果中各阶固有频率可以发现, 3种质量布置方式的一阶固有频率基本不变, 而二阶扭转模态固有频率随着分布质量块质心距离的增大迅速下降, 最后接近一阶固有频率。当间距为12 mm时, 振子的二阶共振频率已经下降到17.2 Hz, 仿真结果中其带宽约为2.3 Hz。试验结果表明, 通过分布式的布置方式可有效地对弯曲模态的共振频率与扭转模态的共振频率进行解耦并实现独立控制, 从而将发电装置的弯曲模态和扭转模态布置到所需的10~20 Hz区间内, 在低频区间内实现高发电效率。
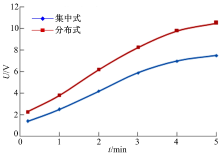
试制分布式压电悬臂梁发电装置与传统的集中质量压电悬臂梁, 并进行装车对比测试, 得到的发电量与时间关系曲线如图6所示, 通过对比结果可看到, 在市区路面进行随机路面状况发电测试, 利用弯曲模态与扭转模态共同构成复合式压电悬臂梁发电装置, 其发电量约为传统集中质量压电发电装置发电量的1.4倍, 性能有明显提升, 完全满足TPMS中分布式传感器、信号处理及发射装置3.7 V工作电压的供电需求, 在汽车运行1 min以内即可提供足够的电压供检测系统正常启动运行。
(1)通过对压电悬臂梁有限元模型的模态分析, 得到了压电悬臂梁前六阶模态的固有频率, 通过参数的合理选择将压电悬臂梁发电装置的一阶弯曲模态固有频率调整到12.6 Hz, 处于振动源频率区间(10~20 Hz)内, 实现了压电发电效果的优化。
(2)在理论分析的基础上提出了一种将悬臂一阶弯曲模态和二阶扭转模态解耦的结构构成方式, 并通过仿真分析了其振动特性, 通过该质量块分布布置的方法设计出了一阶频率12.6 Hz、二阶频率17.2 Hz的压电悬臂梁发电装置。
(3)分布式质量块与集中式质量块发电装置的对比试验结果表明, 前者的发电量为后者的1.4倍, 该方法可明显增强压电悬臂梁的发电能力。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|