作者简介:郭建华(1961-),男,教授,博士.研究方向:机械传动理论及带传动技术,现代机械设计理论与方法.E-mail:guo1034@sina.com
基于Westhoff的同步带与带轮传动啮合干涉评价体系,提出了以人字带齿的包络齿廓与带轮齿槽不干涉作为评判带与轮不产生啮合干涉的新方法。根据人字齿传动特点,设计了一种新型人字齿同步带并建立了求解带共轭齿廓的传动模型。与Eagle PD对比结果表明:新型人字齿同步带传动啮合无干涉;带齿高而陡峭,抗爬齿能力强;带与轮的法面齿形是圆心在节线上圆弧共轭齿,其圆弧半径大,瞬时接触线长,有助于提高带齿接触强度。
A new method was put forward based on Westhoff meshing transmission interference evaluation system. The method was used to judge whether there exists interference between the enveloping tooth profile and pulley tooth groove of the double helical synchronous belt transmission. Then a new double helical synchronous belt was designed and the conjugated tooth profile transmission model was induced on the basis of the double helical transmission characteristics. It is shown that there is no meshing interference in the new double helical synchronous belt compared with the Eagle PD; the higher and steeper the belt tooth, the stronger the resistance ability to climb. The new normal tooth profile is effective to improve the contacting strength while the radius is larger and the instant engagement line is longer, where the point of the conjugated circular arc is on the pitch line.
同步带传动属多柔体系统传动范畴, 由于影响同步带传动啮合干涉因素的复杂性(如节距差、带齿变形和多边形效应等)以及啮合状态的多样性(主、从动轮啮入、啮出), 同步带与带轮齿廓齿形设计较为复杂。为实现带齿廓与带轮齿廓更为平滑地啮合, 自1946年发明同步带传动以来, 带与轮齿廓齿形曲线的形状处于不断地变异、演化过程中。齿廓曲线由最早的直线、渐开线发展到圆弧曲线、抛物线、曳物线等不同曲线齿形, 而齿形曲线由分段曲线连接而成。作为多柔体传动系统的带与带轮刚柔耦合啮合接触干涉问题, 直接影响传动噪声、承载能力和传动精度。研究表明, 同步带与带轮有适量的干涉, 可以降低传动噪声、消除多边形效应、提高传动精度、减少主从动轮的速度波动[1, 2]; 带齿与轮齿齿形影响着侧隙大小, 降低侧隙可以改善带齿间的载荷分布, Gates公司8YU同步带, 通过齿廓修形, 使侧隙从0.393 mm减到0.135 mm, 有利于提高同步带承载能力[3]。
影响直齿同步带传动啮合因素众多, 如多边形效应、带齿变形、节距差等。减小带齿啮入、啮出干涉一直成为同步带齿形研究的重点问题。目前同步带齿廓齿形都为Gates、Goodyear等少数公司研制的专利产品[4, 5, 6]。
本文分别对新型人字齿同步带和美国GoodYear公司Eagle PD人字齿同步带传动进行建模, 对比研究带齿的共轭齿廓与带轮齿槽的齿形干涉情况, 为新型人字齿同步带传动设计提供依据。
多柔体组成的人字齿同步带传动系统, 因带齿与轮齿人字排列, 使带齿槽底与带轮齿顶沿轮齿在圆周方向连续接触, 消除了带轮-带(相当齿条)模型中的多边形效应, 因此人字齿带与带轮传动可以视为人字齿条与带轮传动。
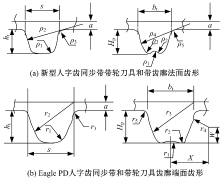
新型人字齿同步带传动在齿形选型上, 采用高阶接触啮合理论, 使带齿具有更大接触强度, 接触点附近间隙为3阶无穷小[7, 8, 9], 满足上述条件的简单齿廓曲线为圆心在节线上的圆弧曲线, 并将圆弧齿廓作为新型人字齿同步带传动法面基准齿廓, 如图1(a)所示。带齿廓由5段圆弧曲线组成, 带轮刀具齿形由直线和3段圆弧组成; Eagle PD人字齿同步带端面为基准齿形, 如图1(b)所示, 带齿是由直线和3段圆弧组成, 带轮刀具由5段圆弧曲线组成[10, 11]。
为便于公式推导及建模, 将基准齿形为法面齿廓的新型人字齿同步带与带轮刀具齿廓, 采用统一建模公式; 将端面为基准齿形的Eagle PD人字齿同步带和带轮刀具齿廓采用统一建模公式。根据人字齿传动特点, 简化建模, 将人字齿传动模型转化为斜齿与斜齿轮传动。研究齿廓是对称的, 故齿廓方程取一侧齿廓建立。
如图1(a)所示, 参数在σ n=[on; xn yn zn]法平面坐标系, ρ i为第i段曲线的圆弧半径; (ρ ix, ρ iy)对应圆心坐标; i=1, 2, …, n; θ 为对应圆弧曲线极坐标的矢径转角; n=5为带齿齿廓方程; n=3为带轮刀具齿廓方程, 带轮直线段方程略, 齿廓法面建模方程为:
基准齿形为端面齿廓的Eagle PD人字齿同步带与带轮刀具齿廓, 如图1(b)所示, 端平面坐标系σ 2=[o2; x2y2]。n=5为Eagle PD带轮刀具齿廓方程, n=3为齿廓方程。齿廓法面建模方程为:
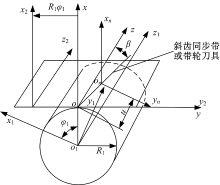
新型人字齿同步带和带轮刀具, 由法面σ n转β 角变换为端面σ 2=[o2; x2y2z2], 如图2所示, 对应空间曲面Σ 2方程为:
同理Eagle PD的人字齿同步带轮刀具、同步带在σ 2坐标系的空间曲面Σ 2方程为:
式中:u为齿面曲线坐标之一, 为齿廓在齿向上的位移。
研究带或刀具的共轭齿廓, 采用齿轮齿条模型, 如图2所示。由带或刀具曲面Σ 2, 利用瞬时回转轴法确定啮合函数, 齿轮齿条传动模型啮合方程为:
式中:R1和φ 1分别代表共轭轮的节圆半径和转角。
根据曲面法矢n2定义, 新型人字齿同步带、带轮刀具在空间曲面Σ 2上有相同形式法矢表达式:
同理Eagle PD同步带、带轮刀具齿廓在空间曲面Σ 2上统一法矢表达式为:
将式(6)代入式(5)中, 新型人字齿同步带、带轮刀具啮合方程为:
将式(7)代入式(5)中, Eagle PD同步带、带轮刀具啮合方程为:
利用坐标系σ 2到坐标系σ 1的变换关系, 得出新型人字齿同步带包络齿廓或带轮齿廓曲面Σ 1方程为:
将人字齿同步带法面齿廓参数和带轮刀具参数分别代入方程(10)可得出带共轭齿廓和带轮齿廓。同理, Eagle PD带轮齿廓或带齿的共轭齿廓曲面Σ 1方程为:
将带轮刀具端面参数和带轮齿廓参数分别代入方程(11)得到带轮齿廓和带的共轭齿廓。
图3所示为Gates公司Westhoff在分析了现有同步带、带轮齿形与传动干涉关系[4]的基础上, 研究了同步带(齿条)与带轮(Z=34)静态啮合状态下带与轮齿齿形与结构参数关系得出的结论:当带齿较低, 带与轮齿存在间隙, 不易产生啮合干涉, 冲击噪声低, 但自锁性差, 载荷变化时易爬齿, 如图3(a)所示。当带齿较高, 带与轮齿侧曲线斜率大, 自锁好, 抗爬齿能力强, 但带与轮齿间有啮合干涉, 冲击噪声大, 如图3(b)所示。Gates公司的G型同步带, 带齿高(节距8 mm, 齿高3.43 mm), 具有很好的抗爬齿特性; 但啮合无干涉, 冲击噪声小, 如图3(c)所示, 适合高速、重载、低噪声传动。
Westhoff[4]对带与轮齿齿形与结构参数关系的研究模型存在两个不足:一是模型忽略了传动的多边形效应; 二是模型仅反映某位置带与轮齿接触状态, 没有反映带齿与轮齿嵌入过程中的情况。通常带齿相对于轮齿做啮入运动, 形成的包络齿廓随轮的半径变化, 一般比实际带齿廓宽。包络齿廓与轮齿槽产生齿形干涉, 可以判定带齿与轮齿啮合传动就不会干涉。
新型人字齿同步带与带轮齿形特点:带齿曲面与带轮齿曲面在齿的法面齿侧弧为共轭齿廓, 其他曲线部分为非共轭齿廓。表1表示两种带与带轮齿廓参数。为了便于研究齿形对干涉的影响, 令齿侧间隙为零。图4表示新型人字齿同步带节线与带轮节圆相切条件下传动模型。因侧隙为零, 带齿根宽与轮齿槽顶相等, 齿条(带)嵌入带轮齿槽中, 没有齿形干涉发生。
| 表1 同步带和带轮刀具基本参数 Table 1 Basic parameters of synchronous belt and pulley mm |
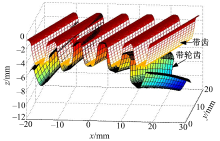
为显示斜齿带与螺旋轮齿间沿齿向啮合状态, 图5表示斜齿带与带轮螺旋齿槽沿齿向不同截面的啮合状态。在齿向方向, 带齿逐渐啮入轮齿槽, 带齿顶与轮齿槽底接触, 齿侧无干涉。齿顶干涉是有益的, 因为带齿顶受力, 可减缓齿根应力集中。
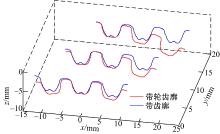 | 图5 新型人字齿同步带与轮啮合传动模型截面图Fig.5 Section graph of meshing transmission model for double helical synchronous belt and pulley |
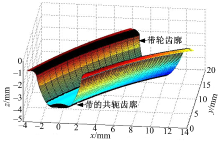
图6是新型人字齿同步带的共轭齿廓与带轮齿廓三维齿形图, 带轮齿槽包容带的共轭齿廓, 齿形无干涉。
 | 图6 新型人字齿同步带共轭齿廓和带轮齿槽齿廓Fig.6 Conjugate tooth profile and pulley groove profile of double helical synchronous belt |
图7是图6端面剖面图, 齿侧共轭部分齿形吻合, 齿顶和齿根非共轭部分齿形无干涉。图8是Eagle PD带共轭齿廓与带轮齿槽三维图, 轮齿槽中下部阴影部分和齿槽底部与带共轭齿廓干涉。
图9是图8的端面剖面图, 实际啮合中, 带齿触及轮槽底就不会向下移动, 因此会产生啮合干涉。这是Eagle PD齿形特点, 带齿顶受接触力, 可以减缓齿根应力集中。带齿顶有较大干涉, 带齿嵌入到带轮齿内部实际不可能发生, 干涉量引起带齿节线径向偏移, 影响传动精度。
 | 图7 新型人字齿同步带共轭齿廓和带轮齿槽端面齿形Fig.7 Conjugate tooth profile and face profile of pulley groove for double helical synchronous belt |
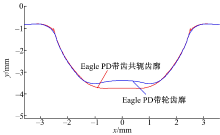 | 图9 Eagle PD共轭齿廓和带轮齿槽端面齿形Fig.9 Conjugate tooth profile and face profile of pulley groove for Eagle PD |
新型人字齿同步带法向齿廓为圆弧齿, 图10(a)是图1法向剖面图, 带齿2与轮齿槽存在间隙。图10(b)表示带齿与轮齿侧弧圆心过啮合轴时, 带右侧齿与轮齿槽形成的瞬时接触线, 因为侧弧半径比Eagle PD侧弧半径大, 瞬时啮合线比Eagle PD更长, 提高了带齿的接触强度。
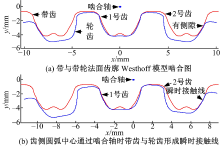 | 图10 法截面上带齿和带轮啮合关系与形成的瞬时接触线Fig.10 Meshing relationship and instantaneous contact line of belt and pulley on normal plate |
如图11所示, 新型人字齿同步带齿比Eagle PD更高, 齿廓截面积更大, 因此带齿可以承受更大的载荷和抗爬齿性能。
(1)建立的以人字齿带齿的包络齿廓与带轮齿槽不干涉作为评判带与轮不产生啮合干涉的新方法比Westhoff提出的干涉判据更合理和准确。
(2)消除传动多边形效应, 带齿与轮齿啮合传动更接近齿轮齿条传动原理, 为人字齿同步带传动齿形设计提供了理论依据。
(3)新型人字齿同步带传动和Eagle PD进行的啮合干涉对比分析表明, 新型人字齿同步带传动啮合更顺滑, 带齿与轮齿廓无齿形干涉, 高带齿使齿廓陡峭, 抗爬齿性能更好。
(4)新型人字齿同步带传动, 齿廓的齿侧齿形为圆弧齿廓, 齿侧半径大, 瞬时接触线长, 有助于提高两齿廓瞬时接触强度。采用零侧隙设计带齿与轮齿的法面齿廓齿形, 啮合传动无干涉, 表明带齿与轮齿啮合更顺滑, 可以实现比直齿同步带更低的侧隙传动。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|