考虑信号特点的合成量子启发结构元素

引用本文

张培林, 陈彦龙, 王怀光, 李胜. 考虑信号特点的合成量子启发结构元素. 2015, 45(4): 1181-1188
ZHANG Pei-lin, CHEN Yan-long, WANG Huai-guang, LI Sheng. Compound quantum-inspired structuring element considering signal characteristics. Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1181-1188 复制到剪切板

Permissions

考虑信号特点的合成量子启发结构元素

张培林, 陈彦龙, 王怀光, 李胜

军械工程学院车辆与电气工程系,石家庄 050003

陈彦龙(1987-), 男, 博士研究生.研究方向:状态监测与信号处理.E-mail:chenyanlong110@163.com

作者简介:张培林(1955-),男,教授,博士生导师.研究方向:车辆维修理论与技术.E-mail:zpl@163.com

基金:国家自然科学基金项目(51205405, 51305454)

摘要

受量子理论启发,结合数学形态滤波器中的膨胀算子,提出合成量子启发结构元素(Compound quantum-inspired structuring element,CQSE),用于增强故障振动信号中的冲击响应成分。CQSE综合考虑了信号的局部特征和随机性,其高度能够跟随信号的变化进行动态调整。首先,建立了量子启发结构元素(Quantum-inspired structuring element,QSE)的基本数学表达式。随后,采用峭度描述冲击响应信号的局部特征,并用于生成QSE在实数空间的单一形式(Single form in real space,SFRS)的高度;采用信号的归一化振动大小描述信号的随机性,并用于计算不同SFRS出现的量子概率。然后,结合量子概率,通过数学期望,对不同的SFRS进行合成,获得应用于膨胀算子的CQSE。最后,将CQSE应用于轴承故障诊断,有效地增强了故障信息。

关键词: 仪器仪表技术; 结构元素; 量子理论; 局部特征; 随机性

中图分类号:TH113.1 文献标志码:A 文章编号:1671-5497(2015)04-1181-08

Compound quantum-inspired structuring element considering signal characteristics

ZHANG Pei-lin, CHEN Yan-long, WANG Huai-guang, LI Sheng

Department of Vehicles and Electrical Engineering, Ordnance Engineering College, Shijiazhuang 050003, China

Abstract

Inspired by the quantum theory, a Compound Quantum-inspired Structuring Element (CQSE) based on morphological dilation operator is proposed to enhance shock response component of fault vibration signals. The CQSE considers both the local feature and stochastic characteristics of the signals, therefore, COSE adjusts its height dynamically according to signal. First, the basic expression of Quantum-inspired Structuring Element (QSE) is proposed. Second, the kurtosis, which is employed to describe the local feature of shock response signals, is utilized to generate the height of Single Form in Real Space (SFRS) of QSE; the normalized signal, which is employed to describe the stochastic characteristics of signals, is utilized to compute quantum-inspired probability of each SFRS. Third, combing quantum-inspired probability with mathematical expectation, the CQSE for morphological dilation operator is obtained. Finally, the CQSE is applied to bear fault diagnosis and enhance the fault information effectively.

Keyword: technology of instrument and meter; structuring element; quantum theory; local feature; stochastic characteristics

Show Figures

0 引言

机械设备发生冲击故障时会产生振动, 其信号概率密度函数峰值大小用陡峭表示, 它反映信号波形中的冲击响应成分的大小, 常用于刻画信号的局部特征^{[1, 2]}。文献[1]基于振动信号的峭度建立阈值降噪方法, 有效提取到信号中冲击响应成分; 文献[2]基于峭度检测出低信噪比信号中的脉冲成分。本文利用峭度定量刻画冲击响应信号的局部特征。

数学形态滤波器(Mathematical morphological filter, MMF)在故障信息分析中表现突出, 近年来得到了广泛关注。文献[3-6]采用MMF完成了机械设备故障的识别, 但滤波过程均采用传统的结构元素(Conventional structuring element, CSE)进行形态分析, 结构元素(Structuring element, SE)的高度不随信号的变化而改变, 忽视了信号的局部特征和随机性, 滤波效果受到限制。为增强MMF对故障振动信号的分析能力, 需要在SE中考虑振动信号的局部特征和随机性, 实现SE高度的动态调整。

MMF中的膨胀算子具有一定的冲击响应信号提取能力^[7], 且膨胀算子为MMF的基本算子, 是组成其他形态运算的基础, 为增大研究内容的应用空间, 本文研究应用于膨胀算子的SE。

近年来量子理论在数据优化^{[8, 9, 10]}、信号传送^{[11, 12, 13]}、图像处理^{[14, 15]}等领域发展迅速, 获得了大量应用, 表明该理论具有巨大的研究价值。本文应用量子理论的知识, 充分考虑信号的局部特征和随机性, 建立合成量子启发结构元素(Compound quantum-inspired structuring element, CQSE), CQSE的高度能够随着信号的变化动态调整, 具有更强的冲击响应信号增强能力。首先, 定性分析了将多量子位量子系统用于表达SE状态的可行性, 并进一步建立了量子启发结构元素(Quantum-inspired structuring element, QSE)的基本数学表达式。随后, 建立了把QSE从量子空间的单一形式(Single form in quantum space, SFQS)映射到实数空间的单一形式(Single form in real space, SFRS)的方法:采用峭度刻画冲击响应信号的局部特征, 作为SFRS在实数空间的高度; 采用信号归一化值建立量子概率幅, 用信号本身的随机信息衡量不同SFRS出现的概率。接下来, 进行展开分析, 结合量子概率, 采用数学期望, 对各个SFRS合成得到了合成量子启发结构元素(Compound quantum-inspired structuring element, CQSE), 并将其用于MMF膨胀运算。最后, 将CQSE应用于轴承故障分析, 对CQSE对冲击响应的增强能力进行了验证。

1 研究内容

本文研究的目标是结合量子理论, 建立一种能够随着信号的局部特征和随机性动态调整高度的SE, 实现冲击响应信号的增强。MMF中有膨胀和腐蚀两个基本算子, 它们是构成其他算子的基础。膨胀算子具有一定的冲击响应信号提取能力, 通过膨胀算子能够建立起更加复杂的滤波器^[6], 为增加研究内容的应用空间, 本文基于膨胀算子进行讨论。

SE为向量, 为了便于描述, 文中将信号同样视为向量。假设输入信号为s(k)(k=1, 2, …, l), 结构元素为g(j)(j=1, 2, …, n)且l≫n。

s(k)关于g(j)的膨胀定义为:

$\begin{matrix} \begin{matrix} (s \oplus g) (k) = \max {s (k - j + 1) + \\ g (j) | j = 1, 2, \dots, n} (1) \end{matrix} \end{matrix}$

2 量子理论的基本概念

2.1 量子位

量子位的状态是|0> 和|1> 两种量子态的线性叠加, 数学表达式如下^{[8, 9, 10]}:

$\begin{matrix} | Ψ > = α | 0 > + β | 1 > (2) \end{matrix}$

式中:α 和β 称为一个量子位的概率幅; |α |²表示被观测到量子态|0> 的概率; |β |²表示被观测到量子态|1> 的概率, α 和β 满足下列归一化条件:

$\begin{matrix} {|α|}^{2} + {|β|}^{2} = 1 (3) \end{matrix}$

2.2 多量子位系统

对基本的量子位进行扩展, 设一个量子系统由n个量子位构成, 其中第j(j=1, 2, …, n)个量子位的状态为:

$\begin{matrix} | Ψ (j) > = w_{0}^{j} | 0 > + w_{1}^{j} | 1 > (4) \end{matrix}$

多量子位量子系统的状态|Ψ > 可表示为^[15]:

$\begin{matrix} \begin{matrix} | Ψ > = (w_{0}^{1} w_{0}^{2} \dots w_{0}^{n}) | 00 \dots 0 > + \\ (w_{0}^{1} w_{0}^{2} \dots w_{1}^{n}) | 00 \dots 1 > + \dots + \\ (w_{1}^{1} w_{1}^{2} \dots w_{1}^{n}) | 11 \dots 1 > = \\ \overset{2^{n} - 1}{\sum_{i = 0}} w_{i} | i_{b} > (5) \end{matrix} \end{matrix}$

基态|i_b> 中的i_b为对应十进制数i的n位二进制形式。w_i为基态|i_b> 的概率幅, 它满足归一化条件:

$\begin{matrix} \overset{2^{n} - 1}{\sum_{i = 0}} | w_{i} |^{2} = 1 (6) \end{matrix}$

多量子位量子系统特殊的叠加态表达方式包含多个基态|I_b> ∈ {|00…0> , …, |i_b> , …, |11…1> }, 如果用不同的基态表示不同的SE, 则多量子位量子系统同时包含SE的多种状态, 有利于实现SE的改变和调整。

3 QSE的建立方法

3.1 量子理论与信号的结合分析

一维机械振动信号为非线性和非稳态, 采用CSE对其进行分析具有先天的不足, 建立能够根据信号发生变化的SE, 将有助于解决这一问题。

多量子位系统的量子位越多, 基态|I_b> 能够代表的状态就越多, 能够为信号提供分析的SE就越多。但随着n的增大, 运算量将按指数级增大, 当n=5时, 有2⁵种SE, 当n=46时, 有2⁴⁶种SE。综合考虑信号分析能力和计算速度, 本文取n=5。

振动信号为实数空间的量, 式(5)在量子空间的二进制表达式无法直接用于信号分析, 接下来将给出把基态|I_b> 从量子空间映射到实数空间的具体方法, 为振动信号分析提供在实数空间可用的SE。

3.2 QSE的基本表达式及其映射方法

首先, 在量子空间建立QSE的基本数学表达式, 定义包含n个量子位的QSE为量子概率幅( $\begin{matrix} w_{j}^{r_{j}} \end{matrix}$ , $\begin{matrix} w_{j}^{0} \end{matrix}$ )(j=1, 2, …, n)的向量:

$\begin{matrix} qs = [(w_{1}^{r_{1}}, w_{1}^{0}), (w_{2}^{r_{2}}, w_{2}^{0}), \dots, (w_{n}^{r_{n}}, w_{n}^{0})] (7) \end{matrix}$

式中: $\begin{matrix} w_{j}^{r_{j}} \end{matrix}$ 表示第j个量子位|i_b> (j)中|1> 状态的概率幅; $\begin{matrix} w_{j}^{0} \end{matrix}$ 表示第j个量子位中|i_b> (j)中|0> 状态的概率幅。结合式(5)可知, 式(7)实质上表达的意义与|I_b> 一致, 但比|I_b> 更加详细, 多出了概率幅内容。经过测量, |I_b> 将成为一个确定的|i_b> , 代表QSE的一个状态, 为了下文叙述方便, |i_b> 称为QSE在量子空间的单一形式(Single form in quantum space, SFQS), SFQS映射到实数空间, 成为QSE在实数空间的单一形式(Single form in real space, SFRS)。SFRS是通过QSE得到的确定的SE, 可用于形态学运算。

建立QSE的映射方法, 使QSE从量子空间映射到实数空间, 完成|I_b> 到具体SE的变化, 映射方法详细说明如下:

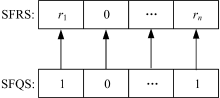
(1)|I_b> (j)发生状态|1> 的概率为| $\begin{matrix} w_{j}^{r_{j}} \end{matrix}$ |², 经过测量, 得到一个确定的SFQS, 将SFQS映射为SFRS, SFRS对应位g(j)=r_j, r_j为局部特征的定量描述, 采用采样点位置的局部峭度。

(2)|I_b> (j)发生状态|0> 的概率为| $\begin{matrix} w_{j}^{0} \end{matrix}$ |², 经过测量, 得到一个确定的SFQS, 将SFQS映射为SFRS, SFRS对应位g(j)=0。

二者的映射关系见图1。

	Figure Option View Download New Window
	图1 SFQS与SFRS的映射关系Fig.1 Mapping from SFQS to SFRS

3.3 基于局部特征的SFRS高度

SE的高度对膨胀结果影响巨大, 给出SFRS高度的具体计算方法如下:

(1)对应状态|1> 的高度r_j

发生机械故障时, 冲击响应属于需要提取出来的信号。峭度指标能够反映信号冲击响应分量的大小, 因此采用峭度^{[1, 2]}来计算r_j。在SFRS中加入冲击响应成分的信息, 便有望在膨胀运算中增强冲击响应信号。在第k个采样点s(k)(k=1, 2, …, l)的局部峭度计算公式为:

$\begin{matrix} K (k) = \frac{1}{5} \overset{2}{\sum_{w = - 2}} {(\frac{sw (k, w) - \bar{sw}}{σ})}^{4} (8) \end{matrix}$

为尽可能地突出冲击响应信号的局部特征, sw为宽度等于5的窗截取的信号段, sw(k, w)=[s(k-2), s(k+w), s(k), …, s(k+2)], $\begin{matrix} \bar{sw} \end{matrix}$ 为sw(k, w)的均值, σ 为sw的标准差。

当膨胀算子处理第k个采样点, 结合式(1)可知, 与SFRS进行运算的数据段为[s(k-n+1), s(k-n+2), …, s(k)], 将SFQS映射为SFRS时, 第j个位置r_j为:

$\begin{matrix} r_{j} = K (k - j + 1) (j = 1, 2, \dots, n) (9) \end{matrix}$

注意, 由于信号具有随机性, 通常r₁≠ r₂≠ …≠ r_n。当|I_b> =|11…1> 时, g=[r₁, r₂…, r_n], SFRS完全由局部峭度决定。

(2)对应状态|0> 的高度0

高度0具有以下两个优点:第一, 采用数值0, 可避免膨胀运算对信号幅值的修改, 同时运算量少, 运算速度快, 有利于本文研究内容与其他算子的结合, 增大应用范围。当|I> =|00…0> 时, SFQS的高度完全为0, SE即为g=[0, 0, …, 0], SE退化为高度为0的扁平型SE, 在机械信号分析中得到了大量应用。第二, 在获得CQSE时, 数值0不会影响CQSE的高度, CQSE的高度将完全由局部峭度来影响r_j。

从SFQS映射为SFRS时, SE高度充分考虑到了冲击响应信号的局部特征, 并利用局部特征对SE的高度进行了调整。在不同的采样点, 通过上述方法获得的高度r_j是不一样的, SFQS映射到SFRS时, 局部峭度信息进入SE, 重点增强冲击响应信号。

3.4 基于信号随机性的量子概率

经过映射, QSE将生成不同的SFRS, 不同的SFRS出现的量子概率不同。量子概率幅( $\begin{matrix} w_{j}^{r_{j}} \end{matrix}$ , $\begin{matrix} w_{j}^{0} \end{matrix}$ )关系到不同SFRS出现的概率, 而不同的SFRS将导致不同的膨胀结果, 因此需要对概率幅进行合理的设置, 对概率的设定主要考虑信号的随机性。

进一步限制, 要求( $\begin{matrix} w_{j}^{r_{j}} \end{matrix}$ , $\begin{matrix} w_{j}^{0} \end{matrix}$ )满足两个条件:

$\begin{matrix} \begin{matrix} 0 \leq w_{j}^{r_{j}} \leq 1 (10) \\ 0 \leq w_{j}^{0} \leq 1 (11) \end{matrix} \end{matrix}$

归一化后的振动信号由于满足式(10)和(11), 可直接用于表示基态的概率幅^{[15, 16]}。对采样信号s(k)进行归一化处理:

$\begin{matrix} z (k) = \frac{s (k) - \min (s (k))}{\max (s (k)) - \min (s (k))} (12) \end{matrix}$

用膨胀算子处理第k个采样点时, 与SFRS进行运算的数据段为[s(k-n+1), s(k-n+2), …, s(k)]。采用振动信号归一化值表示|I_b> (j)的基态|1> 的概率幅:

$\begin{matrix} w_{j}^{r_{j}} = \sqrt[]{z (k - j + 1)} (13) \end{matrix}$

为满足量子系统的归一化条件, 确定|I_b> (j)的基态|0> 的概率幅为:

$\begin{matrix} w_{j}^{0} = \sqrt[]{1 - z (k - j + 1)} (14) \end{matrix}$

式中:j=1, 2, …, n。

将信号的归一化值直接用于生成|I_b> (j)概率幅, 相当于把信号的随机性考虑进了概率幅, 避免了人为设定概率幅带来的影响。

式(13)和(14)的平方等于|I_b> (j)的状态|1> 和|0> 出现的量子概率, 这样QSE不同量子位的基态概率就通过信号直接得到。

当冲击响应出现时, 振动信号会突然增加, 对应的z(k)大, |I_b> (j)为|1> 的量子概率大, 采用局部峭度作为g(j)的概率大; 当冲击响应未出现时, 对应的z(k)小, |I_b> (j)为|0> 的量子概率大, 采用0作为g(j)的概率大。表明采用式(13)和(14)的概率幅, 能够以合理的概率出现与振动信号特征相匹配的SFRS。

3.5 CQSE的计算

在充分考虑信号局部特征和随机性的基础上, SFQS将以不同的概率映射为不同高度的SFRS, 从QSE的展开式出发, 结合量子概率, 采用数学期望, 便能计算出一个综合各个SFRS信息的SE。

将式(7)展开成式(5)的数学形式, 得到QSE在量子空间的展开形式(Expanded form in quantum space, EFQS)qs_ex:

$\begin{matrix} \begin{matrix} qs_ex = w_{1}^{0} \times w_{2}^{0} \times \dots \times w_{n}^{0} | 00 \dots 0 > + \\ w_{1}^{0} \times w_{2}^{0} \times \dots \times w_{n}^{r_{n}} | 00 \dots 1 > + \dots + \\ w_{1}^{r_{1}} \times w_{2}^{r_{2}} \times \dots \times w_{n}^{r_{n}} | 11 \dots 1 > (15) \end{matrix} \end{matrix}$

由于

$\begin{matrix} \begin{matrix} (w_{1}^{0} \times w_{2}^{0} \times \dots \times w_{n}^{0})^{2} + (w_{1}^{0} \times w_{2}^{0} \times \dots \times w_{n}^{r_{n}})^{2} \\ + \dots + (w_{1}^{r_{1}} \times w_{2}^{r_{2}} \times \dots \times w_{n}^{r_{n}})^{2} = \\ ((w_{1}^{0})^{2} + (w_{1}^{r_{1}})^{2}) \times ((w_{2}^{0})^{2} + (w_{2}^{r_{2}})^{2}) \times \dots \\ \times ((w_{j}^{0})^{2} + (w_{j}^{r_{j}})^{2}) \times \dots \times ((w_{n}^{0})^{2} + (w_{n}^{r_{n}})^{2}) (16) \end{matrix} \end{matrix}$

同时

$\begin{matrix} (w_{j}^{0})^{2} + (w_{j}^{r_{j}})^{2} = 1, (j = 1, 2, \dots, n) (17) \end{matrix}$

所以, 式(16)等价于:

$\begin{matrix} \begin{matrix} (w_{1}^{0} \times w_{2}^{0} \times \dots \times w_{n}^{0})^{2} + (w_{1}^{0} \times w_{2}^{0} \times \dots \times w_{n}^{r_{n}})^{2} + \\ \dots + (w_{1}^{r_{1}} \times w_{2}^{r_{2}} \times \dots \times w_{n}^{r_{n}})^{2} = \\ 1 \times 1 \times \dots \times 1 = 1 (18) \end{matrix} \end{matrix}$

式(18)说明式(15)的概率幅满足归一化条件, 且即便在式(12)为0时, 对应|1> 概率幅为0的情况下, 仍然能够保证式(15)的基态概率幅的平方和为1。

经过量子测量后, 式(15)将坍缩到一个具体的基态|I_b> , 即SFQS, 其表达式为qs_m:

$\begin{matrix} qs_m \in {| 00 \dots 0 >, | 00 \dots 1 >, \dots, | 11 \dots 1 >} (19) \end{matrix}$

结合式(5)易知, qs_m的概率幅w_i为:

$\begin{matrix} \begin{matrix} w_{i} \in {w_{1}^{0} \times w_{2}^{0} \times \dots \times w_{n}^{0}, \dots, \\ w_{1}^{r_{1}} \times w_{2}^{r_{2}} \times \dots \times w_{n}^{r_{n}}} (20) \end{matrix} \end{matrix}$

物理世界中, 量子系统只能表现出一个确定的状态, 对EFQS的膨胀运算实际为对SFQS进行膨胀:

$\begin{matrix} s \oplus qs_ex = s \oplus qs_m (21) \end{matrix}$

因此, 量子空间中发生s􀱇qs_m的概率为:

$\begin{matrix} p (s \oplus qs_m) = w_{i}^{2} (22) \end{matrix}$

结合数学期望可知, 对EFQS进行膨胀的期望值为:

$\begin{matrix} E (s \oplus qs_ex) = \overset{2^{n} - 1}{\sum_{i = 0}} w_{i}^{2} \times (s \oplus qs_m) (23) \end{matrix}$

结合映射方法, 将式(19)映射到实数空间, 以不同的概率采用局部峭度或者0作为高度, SFQS则变为SFRS, 其表达式为qs_r:

$\begin{matrix} \begin{matrix} qs_r \in {[0, 0, \dots, 0], [0, 0, \dots, r_{n}], \dots, \\ [r_{1}, r_{2}, \dots, r_{n}]} (24) \end{matrix} \end{matrix}$

式中:[0, 0, …, 0], [0, 0, …, r_n], [r₁, r₂, …, r_n]的量子概率分别对应于SFQS的概率幅w_i的平方。

结合式(23)(24), 确定本文使用的SE为合成量子启发结构元素(Compound quantum-inspired structuring element, CQSE), CQSE为SFRS的合成式qs_rc:

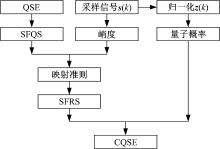
$\begin{matrix} \begin{matrix} qs_rc = (w_{1}^{0} \times w_{2}^{0} \times \dots \times w_{n}^{0})^{2} [0, 0, \dots, 0] + \\ (w_{1}^{0} \times w_{2}^{0} \times \dots \times w_{n}^{r_{n}})^{2} [0, 0, \dots, r_{n}] + \dots + \\ (w_{1}^{r_{1}} \times w_{2}^{r_{2}} \times \dots \times w_{n}^{r_{n}})^{2} [r_{1}, r_{2}, \dots, r_{n}] \\ (25) \end{matrix} \end{matrix}$

CQSE生成过程如图2所示。

	Figure Option View Download New Window
	图2 CQSE生成过程Fig.2 Generating process of CQSE

3.6 CQSE性质分析

由式(25)可知, 本文采用的CQSE为全部SFRS的合成, 不同SFRS所占的权重由量子概率决定。结合式(13)(14), 可知CQSE具备以下性质:

(1)|I_b> (j)中与冲击响应相关的位置取|1> 的概率大, 映射到实数空间, g(j)中与冲击响应相关的位置取局部峭度的概率大, 因此CQSE中局部峭度所占的比重大, 膨胀后冲击响应信号增强的可能性很大。

(2)|I_b> (j)中与冲击响应不相关的位置取|0> 的概率大, 映射到实数空间, g(j)中与冲击响应相关的位置取0的概率大, 因此CQSE中局部峭度所占的比重小, 膨胀后非冲击响应信号增强的可能性小。

(3)局部峭度才能够影响CQSE的高度, 因此从本质上说, CQSE的高度完全由局部峭度和SFRS对应的量子概率决定。

(4)在不同的采样点, CQSE往往不同, CQSE随着信号的变化而动态调整高度。

(5)由于CQSE包含了不同的SFRS, 不同的SFRS可以处理不同的形状, 使用MMF进行信号处理时, 可同时对不同的形状进行分析, 具有更强的形态滤波能力。

3.7 计算复杂度分析

(1)CQSE的计算复杂度

假设计算一次峭度的时间为T₁, 生成一次SFRS高度的时间为T₂, 计算一次SFRS中|I_b> (j)的概率幅时间为T₃, 计算一次SFRS的量子概率的时间为T₄, 计算一次SFRS与量子概率相乘的时间为T₅, 式(25)中相加一次的时间为T₆, 生成一个SFRS时计算峭度的次数为m₁, 生成一个SFRS时产生高度的次数为m₂, 生成一个SFRS时计算|I_b> (j)概率幅次数为m₃, 计算SFRS量子概率的次数为m₄, 计算SFRS与量子概率相乘的次数为m₅, 式(25)中相加的次数为m₆。易知m₁=m₂=m₃, m₁数值等同于量子系统的位数; m₄=m₅=m₆+1, 且m₄与SFRS的个数相等。CQSE的时间复杂度分析结果如表1所示。

表1 CQSE的时间复杂度分析 Table 1 Time complexity analysis of CQSE

所以, 计算一个CQSE总的时间T_CQSE为:

$\begin{matrix} \begin{matrix} T_{CQSE} = m_{1} \times m_{4} \times T_{1} + m_{2} \times m_{4} \times T_{2} + \\ m_{3} \times m_{4} \times T_{3} + m_{4} \times T_{4} + m_{5} \times T_{5} + m_{6} \times T_{6} (26) \end{matrix} \end{matrix}$

由于m₁=m₃, m₄=m₅=m₆+1, 因此:

$\begin{matrix} \begin{matrix} T_{CQSE} = m_{1} \times m_{4} \times T_{1} + m_{1} \times m_{4} \times T_{2} + \\ m_{1} \times m_{4} \times T_{3} + m_{4} \times T_{4} + m_{4} \times \\ T_{5} + (m_{4} - 1) \times T_{6} (27) \end{matrix} \end{matrix}$

总的时间复杂度为:

$\begin{matrix} O (T_{CQSE}) = m_{1} \times m_{4} (28) \end{matrix}$

由计算过程可知:

$\begin{matrix} 2^{m_{1}} = m_{4} (29) \end{matrix}$

总的时间复杂度可进一步约简为:

$\begin{matrix} O (T_{CQSE}) = m_{1} \times 2^{m_{1}} (30) \end{matrix}$

CQSE的计算复杂度由多量子位系统的位数决定。

(2)CSE的计算复杂度

假设CSE长度为m₇, 产生一个高度的时间为T₇, 计算一个CSE总的时间T_CSE为:

$\begin{matrix} T_{CSE} = m_{7} \times T_{7} (31) \end{matrix}$

总的时间复杂度为:

$\begin{matrix} O (T_{CSE}) = m_{5} (32) \end{matrix}$

本文采用5个量子位的系统, 因此O(T_CQSE)=160; 本文在实验中设置CSE长度为最优长度46, 因此O(T_CSE)=46。随着多量子位系统位数的增加, CQSE的计算量会迅速上升, 因此建议采用量子位数较少的多量子位系统, 这也说明了3.1节采用n=5的合理性。

4 应用分析

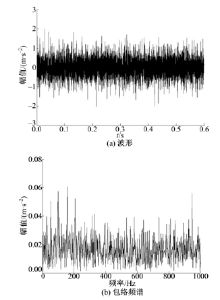
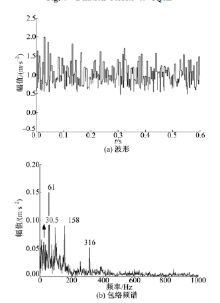
采用某新型机械设备的综合传动装置搭建实验平台, 在轴承内圈上加工出1 mm× 0.3 mm(长× 深)的划痕。采集加速度振动信号, 实测转速为1830 r/min(对应转频为30.5 Hz), 传感器安装在故障轴承箱盖上方。采样频率为12 kHz, 采样时间为0.6 s。理论计算得出内圈故障特征频率为158 Hz。故障信号如图3所示, 包络谱中特征频率淹没在其他频率中, 无法完成故障诊断。

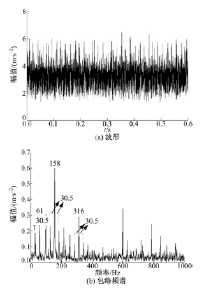
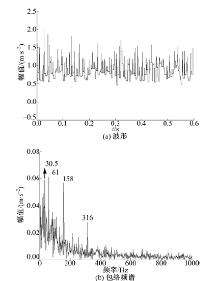
	Figure Option View Download New Window
	图3 含强噪声故障信号Fig.3 Fault signal with strong noise

分别采用CQSE和CSE进行膨胀分析, 结果如图4、图5所示, 同时采用CSE进行闭运算(该方法提取冲击响应的能力更强), 结果如图6所示。根据文献[17]将CSE设置为最优尺寸46且高度为0的扁平SE。从波形图中观察, 3种方法都提取出冲击响应成分, 但采用CSE的膨胀运算提取出的波形有所变形, 信号变为阶梯型, 采用CSE的闭运算和采用CQSE的膨胀运算则较好地保持了细节。

	Figure Option View Download New Window
	图4 CQSE膨胀结果Fig.4 Dilation results of CQSE

	Figure Option View Download New Window
	图5 CSE膨胀结果Fig.5 Dilation results of CSE

观察频谱, 与图3(b)相比, 3种方法均能观察到特征频率158 Hz及其倍频316 Hz, 采用CSE的闭运算和采用CQSE的膨胀运算得到的频谱中转频30.5 Hz及其二倍频61 Hz更加突出, 从这个角度上说, 二者的信号处理效果强于采用CSE的膨胀运算。比较图4、图5、图6, 采用CQSE获得频谱干扰频率少, 特征频率及其倍频更容易观察。除此之外, 仅在图4(b)中, 158 Hz及316 Hz明显存在间隔为30.5 Hz的边带, 与转频相等。综上, CQSE膨胀滤波后所得频谱符合轴承内圈故障的频谱特点,

	Figure Option View Download New Window
	图6 CSE闭运算结果Fig.6 Closing results of CSE

故障诊断效果更佳, CQSE对冲击响应信号的增强能力良好, 且对冲击响应信号的细节保持效果更佳。

为更加客观地评价CQSE对冲击响应信号的增强能力, 采用特征频率强度系数对处理后的信号评价, 特征频率强度系数C_f定义为^[4]:

$\begin{matrix} C_{f} = \overset{N}{\sum_{i = 1}} F C_{i} / \overset{M}{\sum_{j = 1}} F_{j} \end{matrix}$

式中:F_j代表频谱中的各频率的大小; FC_i为特征频率的大小, 本文取N=2。C_f表示特征频率在整个频谱图中所占的能量, C_f越大, 表明特征频率越容易观察。表2比较了采用CQSE和CSE获得的C_f, CQSE效果最佳。

表2 特征频率强度系数比较 Table 2 Comparision of C_f

5 结束语

引入量子理论知识, 提出一种充分考虑信号局部特征和随机性的CQSE, 实现了SE高度的动态调整, 将CQSE应用于MMF的膨胀算子进行轴承故障振动信号分析, 结果表明CQSE具备很强的冲击响应信号增强能力。CQSE与CSE相比, 具备两个优势:①CQSE的高度跟随信号的局部特征进行动态调整, 具备更强的适应能力, 解决了CSE分析非稳态非线性信号的不足; ②采用信号的随机性生成的量子概率, 确保了CQSE可对振动信号中不同的形状进行分析, 而CSE往往只能对某些特定的形状进行提取。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	隋文涛, 张丹. 基于峭度的阈值降噪方法及在振动信号分析中应用[J]. 振动与冲击, 2013, 32(7): 155-158. Sui Wen-tao, Zhang Dan. Kurtosis-based threshold denoising method and its application in vibration signal analysis[J]. Journal of Vibration and Shock, 2013, 32(7): 155-158. [本文引用:2]
[2]	Gervaise C, Barazzutt A, Busson S, et al. Automatic detection of bioacoustics impulses based on kurtosis under weak signal to noise ratio[J]. Applied Acoustics, 2010, 71: 1020-1026. [本文引用:2]
[3]	Dong Y B, Liao M F, Zhang X L, et al. Faults diagnosis of rolling element bearings based on modified morphological method[J]. Mechanical Systems and Signal Processing, 2011, 25: 1276-1286. [本文引用:1]
[4]	Li B, Zhang P L, Wang Z J, et al. A weighted multi-scale morphological gradient filter for rolling element bearing fault detection[J]. ISA Transactions, 2011, 50: 599-608. [本文引用:1]
[5]	Li H, Xiao D Y. Fault diagnosis using pattern classification based on one-dimensional adaptive rank-order morphological filter[J]. Journal of Process Control, 2012, 22: 436-449. [本文引用:1]
[6]	Zhang L J, Xu J W, Yang J H, et al. Multiscale morphology analysis and its application to fault diagnosis[J]. Mechanical Systems and Signal Processing, 2008, 22: 597-610. [本文引用:1]
[7]	Layeb A. A hybrid quantum inspired harmony search algorithm for 0-1 optimization problems[J]. Journal of Computational and Applied Mathematics, 2013, 253: 14-25. [本文引用:1]
[8]	李兵, 张培林, 米双山. 机械故障信号的数学形态学分析与智能故障诊断[M]. 北京: 国防工业出版社, 2011. [本文引用:2]
[9]	Tsa J, Hsiao F Y, Li Y J, et al. A quantum search algorithm for future spacecraft attitude determination[J]. Acta Astronautica, 2011, 68: 1208-1218. [本文引用:2]
[10]	Niu Q, Zhou T J, Fei M R, et al. An efficient quantum immune algorithm to minimize mean flow time for hybrid flow shop problems[J]. Mathematics and Computers in Simulation, 2012, 84: 1-25. [本文引用:2]
[11]	Fang J B, Jiang Z L, Yiu S M, et al. Checking key integrity efficiently for high-speed quantum key distribution using combinatorial group testing[J]. Optics Communications, 2011, 284: 531-535. [本文引用:1]
[12]	Suchat S, Pornsuwancharoen N, Yupapin P P. Continuous variable quantum key distribution via a simultaneous optical-wireless up-down-link system[J]. Optik, 2010, 121: 1540-1544. [本文引用:1]
[13]	Tomita A, Yoshino K, Nambu Y, et al. High speed quantum key distribution system[J]. Optical Fiber Technology, 2010, 16: 55-62. [本文引用:1]
[14]	Fu X W, Ding M Y, Cai C. Despeckling of medical ultrasound images based on quantum-inspired adaptive threshold[J]. Electronics Letters, 2010, 46(13): 21-22. [本文引用:1]
[15]	Yuan S Z, Mao X, Chen L J, et al. Quantum digital image processing algorithms based on quantum measurement[J]. Optik, 2013, 124: 6386-6390. [本文引用:3]
[16]	付晓薇, 丁明跃, 周成平, 等. 基于量子概率统计的医学图像增强算法研究[J]. 电子学报, 2010, 38(7): 1590-1596. Fu Xiao-wei, Ding Ming-yue, Zhou Cheng-ping, et al. Research on image enhancement algorithms of medical images based on quantum probability statistics[J]. Acta Electronica Sinica, 2010, 38(7): 1590-1596. [本文引用:1]
[17]	Nikolaou N G, Antoniadis I A. Application of morphological operators as envelope extractors for impulsive-type periodic signals[J]. Mechanical Systems and Signal Processing, 2003, 17(6): 1147-1162. [本文引用:1]

2013

0.0

. 2013, 32(7):155-158 DOI:doi:10.3969/j.issn.1000-3835.2013.07.031

Kurtosis-based threshold denoising method and its application in vibration signal analysis

基于峭度的阈值降噪方法及在振动信号分析中应用

Sui Wen-tao , Zhang Dan.

隋文涛, 张丹

在分析常用小波去噪方法基础上提出基于振动信号峭度的阈值降噪方法.阈值大小取决于不同尺度上故障信号的小波分解系数.在综合软、硬阈值函数优点基础上提出新的参数可调阈值函数.与常用小波去噪方法进行对比分析结果表明,该方法可有效提取信号中冲击成分.为正确识别故障特征提供有力保证.

... 0 引言机械设备发生冲击故障时会产生振动,其信号概率密度函数峰值大小用陡峭表示,它反映信号波形中的冲击响应成分的大小,常用于刻画信号的局部特征^[1,2] ...

... 峭度指标能够反映信号冲击响应分量的大小,因此采用峭度^[1,2]来计算r_j ...

2010

0.0

... 峭度指标能够反映信号冲击响应分量的大小,因此采用峭度^[1,2]来计算r_j ...

2011

0.0

2011

0.0

... 为更加客观地评价CQSE对冲击响应信号的增强能力,采用特征频率强度系数对处理后的信号评价,特征频率强度系数C_f定义为^[4]: ...

2012

0.0

2008

0.0

... 膨胀算子具有一定的冲击响应信号提取能力,通过膨胀算子能够建立起更加复杂的滤波器^[6],为增加研究内容的应用空间,本文基于膨胀算子进行讨论 ...

2013

0.0

... MMF中的膨胀算子具有一定的冲击响应信号提取能力^[7],且膨胀算子为MMF的基本算子,是组成其他形态运算的基础,为增大研究内容的应用空间,本文研究应用于膨胀算子的SE ...

2011

0.0