防撞梁热冲压模具冷却系统的数值分析及优化

引用本文

谷诤巍, 陆冠含, 李欣, 房欢欢, 徐虹. 防撞梁热冲压模具冷却系统的数值分析及优化. 2015, 45(4): 1189-1194
GU Zheng-wei, LU Guan-han, LI Xin, FANG Huan-huan, XU Hong. Numerical analysis and optimization of cooling system of anti-collision beam hot stamping die. Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1189-1194 复制到剪切板

Permissions

防撞梁热冲压模具冷却系统的数值分析及优化

谷诤巍, 陆冠含, 李欣, 房欢欢, 徐虹

吉林大学材料科学与工程学院,长春 130022

李欣(1980-),女,副教授,博士.研究方向:材料合成与加工工艺.E-mail:li_xin@jlu.edu.cn

作者简介:谷诤巍(1970-),男,教授,博士.研究方向:板料成形.E-mail:wg0919@126.com

基金:吉林省科技发展计划项目(20080507,20110301)

摘要

以防撞梁热冲压模具冷却系统作为研究对象,依据对流传热及流体原理,结合边界层理论对冷却系统传热进行分析,提出冷却系统设计方案,利用Fluent软件模拟模具冷却效果,优化冷却系统直至模拟结果满足要求并通过试验加以验证。结果表明在模具设计中,管道半径 R越大,管道侧壁间距 L、管道顶部至模面的垂直距离 H越小,板料冷却速率越大,其中 H对于模具冷却速率的影响较大, L对于最大温差影响较大。通过对 R、 L、 H的选择与局部调整使板料在均匀冷却的前提下完成马氏体转变。此外,冷却系统的设计还需保证模具的结构强度以及长期工作中能够保持热稳定性。

关键词: 材料合成与加工工艺; 防撞梁; 热冲压模具; 冷却系统; 边界层

中图分类号:TG76 文献标志码:A 文章编号:1671-5497(2015)04-1189-06

Numerical analysis and optimization of cooling system of anti-collision beam hot stamping die

GU Zheng-wei, LU Guan-han, LI Xin, FANG Huan-huan, XU Hong

College of Materials Science and Engineering, Jilin University,Changchun 130022,China

Abstract

Taking the cooling system of anti-collision beam hot stamping die as the research object, the heat transfer in this system is analyzed based on the convection heat transfer and fluid principle combined with the boundary layer theory. A design scheme of the cooling system is put forward, and its cooling effect is simulated using software Fluent. The cooling system is numerically optimized until the simulation results meet the design requirements. Experiment is carried out to verify the numerical optimization. Results show that in the die design, larger pipe radius ( R), smaller pipe sidewall spacing ( L), and smaller vertical distance between pipe top and die surface ( H) lead to larger sheet metal cooling rate. Among them, H has larger influence on die cooling rate and L has larger influence on the maximum temperature difference. The martensitic transformation of the sheet metal is realized under the premise of uniform cooling by partial adjusting parameters R, L and H. Furthermore, in the design, the structural strength and thermal stability of the cooling system for long-term work are considered.

Keyword: materials synthesis and processing technology; anti-collision beam; hot stamping die; cooling system; boundary layer

Show Figures

热冲压成形过程中模具的冷却效果对于热冲压件的力学性能及生产效率起决定作用, 因此, 热冲压模具冷却系统的研究具有重要意义。针对热冲压模具冷却系统, 国内外学者利用理论解析、数值分析及试验等手段进行研究, 一般针对U形件模具研究较多^{[1, 2]}。本文则针对W形件模具冷却系统进行研究, 着重研究防撞梁热冲压模具的冷却系统, 依据对流传热及流体原理, 并利用FLUENT软件进行数值分析, 对模具冷却系统进行设计优化直至满足要求。

1 流体与传热理论基础

1.1 热冲压模具冷却系统的传热原理

对于模具与板料之间、模具内部而言主要以热传导方式传递热量, 由傅里叶定律式(1)可知, 其他条件不变, 温度梯度越大, 传热速率越大。

$\begin{matrix} Q = - λA \frac{dt}{dx} (1) \end{matrix}$

式中:Q为传热速率, W; A为传热面积, m²; λ 为导热率, W∕ (m· K); dt/dx为沿x方向的温度梯度。

在热冲压冷却过程中, 对流传热的驱动力在于管道壁与水流的温差, 得牛顿冷却公式:

$\begin{matrix} Q = αAΔt = \frac{Δt}{\frac{1}{(} αA)} (2) \end{matrix}$

式中:Δ t为对流传热温差, ℃; α 为对流传热系数, W∕ (m²· K)。

由牛顿冷却公式可知, 增大温差可有效提高对流传热速率。

此外, 在一定范围内, 水流速率越大, 传热速率越大。当水流速率达到临界流速后, 水流速率的增加对于冷却效果无明显影响^[3]。选择高于临界流速的水流速度10 m/s。

引入雷诺数(Re)定义

$\begin{matrix} Re = \frac{vdρ}{μ} (3) \end{matrix}$

式中:v为管道内流体的截面平均流速, mm/s; d为管道内径, mm; ρ 为流体的密度, kg/m³; μ 为流体的动力黏度, Pa· s。

计算得Re≥ 10 000, 模具内冷却水流动状态为湍流。

水在模具管道内流动, 在紧靠管道表面形成流速从零急剧增加到与管道内来流同数量级的薄层, 称为边界层^[4]。

可将边界层的传热视为单层圆筒壁的传热, 温度沿半径方向变化, 等温面为同心圆柱面, 设圆筒内半径r₁、外半径r₂、内壁温度t₁、外壁温度t₂、导热率λ 、边界层厚度δ 一定, 在半径r处取厚度dr的薄层, 若管道长度l, 则由傅里叶定律得:

$\begin{matrix} Q = - λA \frac{dt}{dx} = - λ 2 πrl \frac{dt}{dx} (4) \end{matrix}$

分离变量, 进行积分, 得:

$\begin{matrix} Q \int_{r_{1}}^{r_{2}} \frac{dr}{r} = - 2 πlλ \int_{t_{1}}^{t_{2}} d t (5) \end{matrix}$

求解积分并移项, 得:

$\begin{matrix} Q = 2 πlλ \frac{Δt}{\ln \frac{r_{2}}{r_{1}}} = 2 πlλ \frac{Δt}{\ln \frac{r_{1} + δ}{r_{1}}} (6) \end{matrix}$

其他条件一定时, r₁增大, r₁+δ 增大, 管道面积增大, 传热速率Q增大, 由牛顿冷却定律可知对流传热速率也增大, 由此可知增大管道半径可显著提高模具的冷却速率。

1.2 流体传热对热冲压模具冷却系统的要求

鉴于模具的冷却属于热传导与对流换热共同作用, 热冲压模具中管道设置需遵循以下要求:

(1)速度与温度梯度的提高可明显提高换热速率, 设计模具时应尽量提高水流速度使之高于临界流速; 由于生产中用水多为常温, 应尽量减小管道至型面距离以提高温度梯度。

(2)增大管道半径有助于提高传热速率, 因此管道设计时, 应在条件允许的范围内选用较大的管径。

(3)其他参数一定时, 较小的管道间距有助于增加水与管道的接触面积, 因此应选择较小的模具间距。

2 数值模拟模型的建立

2.1 数学模型

由于流动为不可压缩流动且速度远小于声速, 其控制方程组如式(7)(8)(9)所示。

连续性方程

$\begin{matrix} \nabla \cdot v = 0 (7) \end{matrix}$

动量方程

$\begin{matrix} \frac{\partial v}{\partial t} + (\nabla \cdot v) v = - \frac{\nabla p}{ρ} + \frac{μ}{ρ} \nabla^{2} v (8) \end{matrix}$

能量方程

$\begin{matrix} \begin{matrix} ρ c_{p} (\frac{\partial E}{\partial t} + u \frac{\partial E}{\partial x} + v \frac{\partial E}{\partial y} + w \frac{\partial E}{\partial z}) = \\ λ (\frac{\partial^{2} E}{\partial x^{2}} + \frac{\partial^{2} E}{\partial y^{2}} + \frac{\partial^{2} E}{\partial z^{2}}) (9) \end{matrix} \end{matrix}$

式中:u、v、w分别为x、y、z方向的速度; c_p为水的比热容; E为能量; λ 为水的热导率; v为水流速度; p为水压; ρ 为水的密度; μ 为水的动力黏性系数。

2.2 边界条件

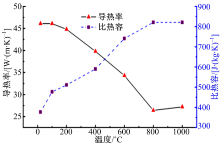
本文中分析的防撞梁见图1。模具的冷却方式为水冷。模具材料为Cr7V, 板料材料为22MnB5。Cr7V的c_p=461 J/(kg· K), 导热率λ =38 W/(m· K), 板料热学性能如图2所示^[5]。模具与板料之间的换热系数h₁=4500 W/(m²· K), 板料与空气的换热系数如图3所示^[6]。由牛顿冷却公式计算得模具冷却管道水与模具之间对流换热系数约为30000 W/(m²· K), 模具与空气的换热忽略。

	Figure Option View Download New Window
	图1 防撞梁示意图Fig.1 Schematic diagram of anti-collision beam

	Figure Option View Download New Window
	图2 22MnB5热学性能随温度的变化曲线Fig.2 Thermal property curve of 22MnB5 change along with the temperature

在冷却过程中, 传热主要发生在模具与板料、模具与水、模具内部、模具与空气以及板料与空气之间^[7]。考虑到从加热炉转移至模具以及冲压过程的热量损失, 板料初始化温度为850 ℃。周围环境温度为25 ℃。在水流入口处设置水流速度为10 m/s, 水温为20 ℃^{[8, 9]}, 凸凹模管道中水流方向相反, 以保证板料沿长度方向冷却均匀。

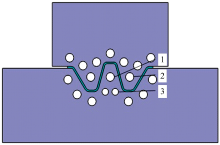
本文中选择防撞梁模具中的单个模块作为研究对象, 建立模型如图4所示。

采用GAMBIT建立模型, 在模拟运算中采用SIMPLE算法, 模拟选择N-S方程与k-ε 湍流模型。在模型导入FLUENT中运算时采用三维单精度运算。

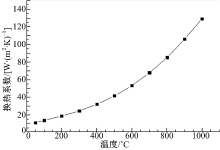	Figure Option View Download New Window
	图3 板料与空气换热系数随温度变化曲线Fig.3 Heat transfer coefficient between sheet metal and air change along with temperature

	Figure Option View Download New Window
	图4 防撞梁热冲压模具模块剖切示意图Fig.4 Cutting of anti-collision beam hot-stamping die

3 数值分析与讨论

3.1 冷却管道R、L、H的选择

在热冲压模具的冷却系统中, 模具的冷却管道半径R、管道侧壁间距L、管道顶部至模面的垂直距离H参数的选择对板料冷却效果至关重要。由连续性方程可得:

$\begin{matrix} n v_{2} π R^{2} = v_{0} A_{0} (10) \end{matrix}$

式中:n为管道数量; v₁为管道内水流平均速度, m/s; R为管道半径, mm; v₀为入水口水流速度, m/s; A₀为入水口面积, mm²。

取管道平均流速为v₁=30 m/s。计算得n=9时, 应取R=4 mm; n=7时, 应取R=5 mm。因此对于管道尺寸应选择R=4或R=5。

根据模具尺寸, 选取R、L、H参数并建立8组模型进行比较, 即Ⅰ :R=5, L=16, H=3; Ⅱ :R=5, L=16, H=6; Ⅲ :R=5, L=19, H=3; Ⅳ :R=5, L=19, H=6; Ⅴ :R=4, L=16, H=3; Ⅵ :R=4, L=16, H=6, Ⅶ :R=4, L=19, H=3, Ⅷ :R=4, L=19, H=6。模拟得钢板在模具中保压淬火10 s后模具与零件的瞬态温度分布如图5所示, 各方案中板料温度情况如表1所示。

	Figure Option View Download New Window
	图5 t=10 s时模具与零件的瞬态温度分布Fig.5 Transient temperature distributions of die and parts with t=10 s

表1 冷却10 s后8种方案的板料温度 Table 1 Temperature of sheet metal in 8 solutions after 10 s'refrigeration

由表1可知, H、L一定时, R越大越有利于冷却; H、R一定时, L越小越有利于冷却; L、R一定时, H越小越有利于冷却。其中H对于模具冷却速率的影响较大, 而L对于最大温差影响较大。

3.2 模具方案的分析与改进

尽管H对冷却速率影响较大, 但是出于结构强度与冷却效果的考虑, 应选择较大的R、H与较小的L参数, 选择H=6, L=16, R=5。其冷却10 s后板料温度云图见图6。要求在保证冷却速率的同时板料最大温差不超过10 ℃, 由于方案Ⅱ 中最大温差13 ℃依旧过大, 根据板料温度分布对模具部分管道R、H参数进行调整, 得改进后管道排布见图7。

	Figure Option View Download New Window
	图6 冷却10 s后方案Ⅱ 的板料温度云图Fig.6 Contours of sheet metal temperature after 10 s'refrigeration in solutionⅡ

	Figure Option View Download New Window
	图7 改进后的模具管道设计图Fig.7 Pipeline design after modification

图7中管道排布左右对称, 管道1、2中H=10; 管道3中R=4。其余参数均不变。

3.3 改进方案的测试

根据图7中改进后的管道建立模型, 模拟得10 s后板料温度分布如图8所示, 板料冷却温度曲线如图9所示。

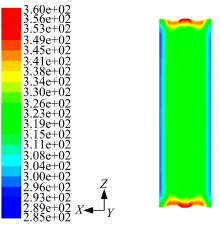	Figure Option View Download New Window
	图8 修改后的模具冷却10 s后的板料温度云图Fig.8 Contours of sheet metal temperature after 10 s'refrigeration in modified die

	Figure Option View Download New Window
	图9 改进后模具中板料的冷却曲线Fig.9 Cooling curve of sheet metal in die after modification

在板料完成马氏体转变的温度区间, 临界冷却速率为30 ℃/s^[10]。由冷却曲线可知, 改进后的模具中板料在马氏体转变温度区间的冷却速率明显大于30 ℃/s。改进后的模具在冷却10 s后板料最低温度为317.5 K, 最高温度为326 K, 板料温度分布更趋均匀, 板料最大温差为8.5 ℃, 板料温度较低, 冷却效果良好, 满足模具冷却系统设计要求。

此外, 考虑到模具需长期工作, 需在多次冲压后保持热稳定, 即模具中冷却水能够及时带走积累的热量, 使模具温度保持稳定, 这里以10 s为一个周期进行冷却, 每隔10 s对板料温度850 ℃进行初始化, 每个周期开始时凸凹模的最高温度如图10所示。

由图10可知, 在连续进行多个周期后, 模具中凸凹模的最高温度保持在150~160 ℃, 温度稳定且不会对模具性能与精度产生明显影响。故该模具冷却系统设计满足要求。

	Figure Option View Download New Window
	图10 以10 s为周期每次冲程开始时凸凹模的最高温度Fig.10 Highest temperature of punch and die at the start of each travel with 10 s as a cycle

4 防撞梁热冲压试验验证

根据优化设计后的管道设计加工的模具、冲压成形件及热冲压件微观组织如图11所示, 根据试验, 模具保压10 s后在本文优化设计的模块段, 板料最高温度为54 ℃, 最低温度为45 ℃, 板料为均匀马氏体组织, 在连续冲压10次后, 凸凹模最高温度分别为151 ℃、153 ℃, 由试验结果可知, 模具模块设计满足要求。

	Figure Option View Download New Window
	图11 防撞梁热冲压模具、热冲压成形件与热冲压件微观组织Fig.11 Anti-collision beam hot-stamping die, hot stamping part and its microstructure

5 结论

(1)在模具管道中R越大, L、H越小, 板料冷却速率越大, 其中H对于模具冷却速率的影响较大, L对于最大温差影响较大。

(2)通过对R、L、H的选择与局部调整可使优化设计后模具中成形件快速均匀冷却, 并通过试验验证了优化结果的可靠性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	蔡玉俊, 陈树来, 王玉广. 高强钢板热冲压模具冷却水道优化设计[J]. 农业机械学报, 2013, 44(1): 252-257. Cai Yu-jun, Chen Shu-lai, Wang Yu-guang. Optimization design on cooling water channel of hot stamping mold of high strength steel[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(1): 252-257. [本文引用:1]
[2]	Cui Jun-jia, Lei Cheng-xi, Xing Zhong-wen, et al. Prediction of mechanical properties and microstructure evolution of high strengh steel in hot stamping[J]. Journal of Materials Engineering and Performance, 2012, 21(11): 2244-2254. [本文引用:1]
[3]	王立影, 林建平, 朱巧红, 等. 热冲压成形模具冷却系统临界水流速度研究[J]. 机械设计, 2008, 25(4): 15-17. Wang Li-ying, Lin Jian-ping, Zhu Qiao-hong, et al. Research on critical water flow speed of hot stamping die cooling system[J]. Journal of Machine Design, 2008, 25(4): 15-17. [本文引用:1]
[4]	王志魁. 化工原理[M]. 3版. 北京: 化学工业出版社, 2004. [本文引用:1]
[5]	徐勇. 超高强度可淬火钢板热成形工艺数值模拟研究[D]. 长春: 吉林大学材料科学与工程学院, 2010. Xu Yong. Research on numerical simulation of hot stamping process of quenchable ultra high strength steel[D]. Changchun: College of Materials Science and Engineering, Jilin University, 2010. [本文引用:1]
[6]	Shapiro Arthur B. Using LS-Dyna for hot stamping[C]∥The 7th European LS-DYNA Conference, 2009. [本文引用:1]
[7]	Karbasian H, Tekkaya A. A review on hot stamping[J]. Journal of Materials Processing Technology, 2010(15): 2103-2118. [本文引用:1]
[8]	Lei Cheng-xi, Cui Jun-jia, Xing Zhong-wen, et al. Investigation of cooling effect of hot-stamping dies by numerical simulation[C]∥International Conference on Solid State Devices and Materials Science, 2012. [本文引用:1]
[9]	Hoffmann H, So H, Steinbeiss H. Design of hot stamping tools with cooling system[J]. CIRP Annals-Manufacturing Technology, 2007, 56(1): 269-272. [本文引用:1]
[10]	Nishibata Toshinobu, Kojima Nobusato. Effect of quenching rate on hardness and microstructure of hot-stamped steel[J]. Journal of Alloys and Compouds, 2010, 96(7): 549-554. [本文引用:1]

2013

0.0

. 2013, 44(1):252-257 DOI:doi:10.6041/j.issn.1000-1298.2013.01.047

Optimization design on cooling water channel of hot stamping mold of high strength steel

高强钢板热冲压模具冷却水道优化设计

Cai Yu-jun , Chen Shu-lai , Wang Yu-guang.

蔡玉俊, 陈树来, 王玉广

The temperature distribution of parts and mould was simulated by ANSYS/LS—DYNA. The shortcomings of the uniform waterway were analyzed. APDL was applied over the thermal field simulation. Zero-order search and fist-order search was combined as the optimization algorithm. In this program, the radius of holes, the distances of adjacent holes and the distances of holes and the profile were chosen as optimization variables. The well-distributed temperature of parts and the needed critical cooling rate were chosen as the optimization objectives to create the objective function. Objective function value was 26.553 after the optimization which was 64.404 before the optimization. By comparing the temperature distribution of the optimized cooling water channel with original, it can be seen that the maximum temperature was decreased by 44.5% and the lowest temperature was decreased by 14.5%, to realize the optimization design of parameters of the cooling water channel. Finally the experiment had been designed to verify the correctness of the optimization result.

利用ANSYS/LS—DYNA模块对保压淬火过程零件及模具的温度场分布进行了数值模拟，分析高强钢板热冲压模具冷却系统均布水道的不足。在此基础上通过APDL参数化编程语言，选择零阶与一阶搜索相结合的优化算法，编写优化程序，以模具冷却水道半径、相邻水道间隔尺寸和水道与模面距离等参数为优化变量，以板料温度分布均匀和保证降温速率达到临界冷却速率为优化目标建立目标函数，优化后目标函数值为26.553（优化前为64.404）。对优化前后成形件的温度分布进行了比较，得到成形件最高温度下降了44.5%，最低温度下降了14.5%，实现了对冷却水道各参数的优化。最后通过实验验证了优化结果的正确性。

... 针对热冲压模具冷却系统,国内外学者利用理论解析、数值分析及试验等手段进行研究,一般针对U形件模具研究较多^[1,2] ...

2012

0.0

... 针对热冲压模具冷却系统,国内外学者利用理论解析、数值分析及试验等手段进行研究,一般针对U形件模具研究较多^[1,2] ...

2008

0.0

. 2008, 25(4):15-17

Research on critical water flow speed of hot stamping die cooling system

热冲压成形模具冷却系统临界水流速度研究

Wang Li-ying , Lin Jian-ping , Zhu Qiao-hong

王立影, 林建平, 朱巧红

为保证热冲压过程中模具具有良好散热效果,优化超高强度钢板热冲压成形模具冷却系统设计,提出热成形模具冷却系统中的临界水流速度.采用解析法建立热冲压模具冷却系统中模具与支撑柱及水流传热模型,获得临界水速的解析公式;通过计算机数值模拟的方法,分析了冷却水流速度对模具向支撑柱和向水流传热的热流密度的影响,验证了临界水速的存在性,继而探索了临界水速下支撑柱半径对模具散热量的影响.结果表明,热冲压模具冷却系统中,水流速度达到临界水速时,模具冷却系统中支撑柱尺寸及有无支撑柱均不影响模具总散热量,即冷却系统中水流速度为临界水速时,模具设计可不考虑支撑柱尺寸的影响,从而给优化热冲压模具冷却系统设计提供了理论支持.

... 当水流速率达到临界流速后,水流速率的增加对于冷却效果无明显影响^[3] ...

2004

0.0

... 水在模具管道内流动,在紧靠管道表面形成流速从零急剧增加到与管道内来流同数量级的薄层,称为边界层^[4] ...

2010

0.0

. 2010, :-

Research on numerical simulation of hot stamping process of quenchable ultra high strength steel

超高强度可淬火钢板热成形工艺数值模拟研究[D]

Xu Yong.

徐勇

在汽车车身制造技术中,超高强度钢板热成形工艺可在实现车身轻量化的同时提高安全性。热成形工艺过程包含传统板料冲压成形的非线性和大变形,而且受系统温度变化和传热过程的影响很大,是一个非常复杂的接触问题,因此工艺开发周期较长。使用计算机模拟技术辅助超高强度钢板热成形工艺开发可以有效提高工艺开发和模具设计效率。本文根据热成形工艺的特点,使用ABAQUS软件建立了超高强度钢板热成形工艺的有限元模型,对U形件的热成形过程进行了动力显式热力耦合模拟,并基于无模法采用显式一隐式联合分析模拟了开模后工件的回弹。从而完成了全工艺的计算机模拟。通过对不同压边力条件下U形件热成形模拟结果分析,得出了如下结果： (1)压边力对成形过程的作用规律。压边力越大,成形过程中板料变薄和U形件翼边温度降低越严重,成形后工件回弹越小。 (2)板料初始温度对成形过程的影响。板料的初始温度越高,越有利于成形,且成形后工件内部应力应变场分布越均匀。 (3)热成形工艺中固态相变对回弹的影响。固态相变是导致工件回弹的因素之一,但其所占比重较小,且压边力越大,相变引发的回弹越小。 (4)工件在保压淬火过程中温度分布和内部应力应变状态的变化规律,模拟发现通过模内淬火可有效改善工件应力状态。 (5)热成形模具中冷却水平衡温度对工件和模具的温度分布及变化的影响。当冷却水流速为1.5m／s时,冷却水平衡温度越低,对工件和模具的冷却效果越好。冷却水平衡温度保持在30℃以下,即能保证工件完成淬火,再降低平衡水温对工件淬火和模具冷却效果影响较小。

... K),板料热学性能如图2所示^[5] ...

2009

0.0

... K),板料与空气的换热系数如图3所示^[6] ...

0.0

... 在冷却过程中,传热主要发生在模具与板料、模具与水、模具内部、模具与空气以及板料与空气之间^[7] ...

2012

0.0

... 在水流入口处设置水流速度为10 m/s,水温为20 ℃^[8,9],凸凹模管道中水流方向相反,以保证板料沿长度方向冷却均匀 ...

2007

0.0

... 在水流入口处设置水流速度为10 m/s,水温为20 ℃^[8,9],凸凹模管道中水流方向相反,以保证板料沿长度方向冷却均匀 ...

2010

0.0

... 在板料完成马氏体转变的温度区间,临界冷却速率为30 ℃/s^[10] ...