基于损伤-相变本构模型的高强钢热成形数值模拟分析

引用本文

庄蔚敏, 解东旋, 余天明, 于皖东. 基于损伤-相变本构模型的高强钢热成形数值模拟分析. 2015, 45(4): 1206-1212
ZHUANG Wei-min, XIE Dong-xuan, YU Tian-ming, YU Wan-dong. Numerical simulation of hot forming of high-strength steel based on damage-phase transformation constitutive model. Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1206-1212 复制到剪切板

Permissions

基于损伤-相变本构模型的高强钢热成形数值模拟分析

庄蔚敏¹, 解东旋¹, 余天明¹, 于皖东²

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.中国第一汽车集团公司技术中心,长春 130011

解东旋(1989-),男,博士研究生.研究方向:车身结构设计与优化,有限元分析和金属成形技术.E-mail:jiedx14@mails.jlu.edu.cn

作者简介:庄蔚敏(1970-),女,教授,博士生导师.研究方向:车身结构设计与优化,有限元分析和金属成形技术.E-mail:zhuangwm@jlu.edu.cn

基金:国家自然科学基金项目(51375201); 吉林省自然科学基金项目(20130101048JC); 国汽(北京)汽车轻量化技术研究院开发基金项目

摘要

针对目前商用有限元分析软件在模拟高强钢热成形过程中,只能模拟相变过程而无法模拟成形损伤过程这一问题,建立了高强钢热成形损伤-相变本构模型,通过编写该力学模型的用户自定义材料子程序,将其应用于LS-DYNA软件的高强钢热成形数值模拟中,在预测相变演化的同时实现成形损伤演化的预测。对帽形件进行了热成形虚拟试验,试验中马氏体体积分数的最大值出现在帽形件的法兰部位,其均值为98.5%,而成形损伤的最大值则集中在帽形件侧壁的中部,其值达到了0.7,该试验验证了本构模型的有效性,为高强钢热成形的实际生产提供了指导。

关键词: 固体力学; 损伤-相变本构; 高强钢; 热成形; 数值模拟

中图分类号:TG142.1 文献标志码:A 文章编号:1671-5497(2015)04-1206-07

Numerical simulation of hot forming of high-strength steel based on damage-phase transformation constitutive model

ZHUANG Wei-min¹, XIE Dong-xuan¹, YU Tian-ming¹, YU Wan-dong²

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

2.R&D Center, China FAW Group Corporation, Changchun 130011, China

Abstract

In the simulation of hot forming of high-strength steel, the phase transformation process can be simulated using current commercial finite element analysis software; however, the forming damage process can not be simulated. To overcome such problem, a damage-phase transformation constitutive model for high-strength steel hot forming is established. By writing user defined material subroutine of this mechanical model, which is used in LS-DYNA software, the phase transformation process and forming damage process can be simultaneously predicted. Furthermore, hot forming virtual test of cap-shaped parts is conducted. Results show that the maximum value of the volume fraction of martensite appears in the flange portion of the cap-shaped parts, the average volume faction is 98.5%; while the maximum forming damage concentrates in the middle of the side wall of the parts, and its value reaches 0.7. The effectiveness of constitutive model is verified in this test, and this research may provide guidance for actual production of hot forming of high-strength steel.

Keyword: solid-state mechanics; damage-phase transformation constitutive model; high-strength steel; hot forming; numerical simulation

Show Figures

0 引言

目前高强钢被广泛用于制造车身零部件, 这样既减轻了车的质量, 又提高了汽车的碰撞安全性^[1]。在高强钢热成形过程中, 板料上存在着变化的温度场, 在其作用下板料的微观组织和机械性能不断变化, 导致板料的应力场发生变化; 应力场的变化又反作用于温度场, 所以热成形工艺本身就是一个热-力-相变耦合的过程^[2], 这个过程中, 存在着板料成形损伤和微观组织的相变, 而二者会影响零件的成形质量和机械性能。针对上述问题, 国内外很多学者进行了深入研究^{[3, 4, 5, 6, 7]}, Kachanov^[8]通过研究最简单的单轴拉伸脆性损伤破坏, 提出损伤演变方程, Lin等^[9]提出一种基于位错硬化的损伤模型, Watt等^[10]预测了焊接过程中微观组织的演变, 胡平等^[11]建立了热成形热、力、相变耦合本构关系。而目前的有限元分析软件虽可模拟板料热成形时的相变过程, 但对于成形损伤, 其分析模型基于传统宏观力学的相关理论, 无法考虑热成形过程中微孔洞扩散、微裂纹扩展等一系列损伤的累积过程。

本文基于损伤力学及微观相变理论, 建立了高强钢热成形损伤-相变本构模型, 利用FORTRAN语言编写相应的用户材料自定义子程序, 并以22MnB5高强度钢板为研究对象, 进行了帽形件热成形数值模拟研究, 在预测相变演化的同时, 实现了成形损伤演化的预测。

1 损伤本构模型

1.1 损伤本构模型的建立

许多国外学者已对黏塑性本构方程进行了大量研究, 模拟了一系列与时间有关的现象, 如蠕变、再结晶等。与Lin等^[12]在推导蠕变变形本构方程时的方法类似, 本文采用如下损伤力学本构方程:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{ε}}_{e}^{p} = {(\frac{σ_{e} / (1 - f_{d}) - H - k}{K})}^{n_{1}} {(1 - f_{d})}^{- γ_{1}} (1) \\ {\overset{\cdot}{ε}}^{p}_{ij} = \frac{3 S_{ij}}{2 σ_{e}} {\overset{\cdot}{ε}}_{e}^{p} (2) \\ \overset{\cdot}{\bar{ρ}} = A (1 - \bar{ρ}) |{\overset{\cdot}{ε}}_{e}^{p}| - C {\bar{ρ}}^{n_{2}} (3) \\ H = B {\bar{ρ}}^{n_{0}} (4) \\ {\overset{\cdot}{f}}_{d} = D σ_{e} |{\overset{\cdot}{ε}}_{e}^{p}| / {(1 - f_{d})}^{γ_{2}} (5) \\ σ_{ij} = D_{ijkl} (1 - f_{d}) ({ε^{T}}_{kl} - {ε^{p}}_{kl}) (6) \\ D_{ijkl} = \frac{E}{2 (1 + ν)} (δ_{il} δ_{jk} + δ_{i k} δ_{jl}) + \\ \frac{Eν}{(1 + ν) (1 - 2 ν)} δ_{ij} δ_{kl} (7) \end{matrix} \end{matrix}$

式中: $\begin{matrix} {\overset{\cdot}{ε}}_{e}^{p} \end{matrix}$ 是等效塑性应变率; σ _e是等效应力; H是由位错引起的应变强化; 塑性变形时, 微观延性破裂的本质是微孔洞的产生、发展、连接而导致破裂, 为评估载荷作用下材料的损伤程度, 引入损伤变量f_d, 其变化范围为0~1, f_d=0时表示材料没有损伤, f_d=1时表示材料完全失效, 通常认为f_d=0.7时, 材料完全失效; $\begin{matrix} {\overset{\cdot}{ε}}^{p}_{ij} \end{matrix}$ 为塑性应变率分量; S_ij为偏应力分量; $\begin{matrix} \bar{ρ} \end{matrix}$ =(ρ -ρ _i)/ρ _m, ρ _i为材料初始状态下的位错密度, ρ _m为材料可达到的最大位错密度, 且ρ _i≤ ρ ≤ ρ _m, 即0≤ $\begin{matrix} \bar{ρ} \end{matrix}$ ≤ 1; σ _ij是应力张量分量; $\begin{matrix} {ε^{T}}_{kl} \end{matrix}$ 是总应变张量分量; $\begin{matrix} {ε^{p}}_{kl} \end{matrix}$ 是塑性应变张量分量; D_ijkl是四阶刚度张量分量; E是杨氏模量; ν 是泊松比; δ _ij和δ _kl为克罗内克因子, 下标i、j、k、l变化范围为1~3, 重复下标遵循爱因斯坦求和约定。

参数k、K、n₁、B、C、D、E是与温度相关的材料参数, 定义如下:

$\begin{matrix} \begin{matrix} k & = k_{0} \exp (Q_{k} / RT) (8) \\ K & = K_{0} \exp (Q_{K} / RT) (9) \\ n_{1} & = n_{10} \exp (Q_{n} / RT) (10) \\ B & = B_{0} \exp (Q_{B} / RT) (11) \\ C & = C_{0} \exp (- Q_{C} / RT) (12) \\ D & = D_{0} \exp (Q_{D} / RT) (13) \\ E & = E_{0} \exp (Q_{E} / RT) (14) \end{matrix} \end{matrix}$

式中:R为通用气体常数; T为温度; Q为激活能; 其他材料常数按文献[13]确定, 见表1。

表1 硼钢损伤本构模型中的材料常数 Table 1 Material constants in viscoplastic-damage constitutive equations for Boron Steel

1.2 损伤本构模型的验证

将不同温度和应变率下的数值模拟结果与硼钢单拉试验结果^[13]进行对比, 如图1所示, 发现数值模拟结果与试验结果基本一致, 证明该损伤本构模型可以用于高强钢热成形有限元分析。

	Figure Option View Download New Window
	图1 不同温度和应变率下的应力应变曲线试验结果与数值模拟结果对比Fig.1 Comparison of computed and experimental stress-strain relationships at different temperatures and strain rates

2 相变本构模型

2.1 相变本构模型的建立

本文采用的材料模型能够模拟奥氏体组织转化为铁素体、珠光体、贝氏体及马氏体组织的过程。用于模拟奥氏体分解反应方程的一般形式为:

$\begin{matrix} \frac{d X_{i}}{dt} = f (G) f (X_{i}) f (T) f (C) (15) \end{matrix}$

式中:f(G)为奥氏体晶格尺寸对相变的影响函数; f(X_i)为各转化相当前含量对组织转变的影响函数; f(T)为温度对相变的影响函数; f(C)为合金元素对各转化相相变速率的影响函数。

晶格尺寸对相变的影响函数为:

$\begin{matrix} f (G) = 2^{(G - 1) / 2} (16) \end{matrix}$

式中:G为ASTM的奥氏体晶粒尺寸数, 本研究中假设冷却过程中该参数恒定不变。

各转化相当前含量对组织转变的影响函数为:

$\begin{matrix} \begin{matrix} f (X_{i}) = \frac{(X_{i})^{2 (1 - X_{i} \frac{)}{3}} (1 - X_{i})^{2 X_{i} / 3}}{Y} (17) \\ Y = \exp (C_{r} {X_{i}}^{2}) (18) \\ C_{r} = 1.9 C + 2.5 Mn + 9 Ni + \\ 1.7 Cr + 4 Mo - 2.6 (19) \end{matrix} \end{matrix}$

式中:X_i是当前时刻各转化相所占体积分数; 不同相的影响因子Y是不同的, 对于铁素体和珠光体Y=1, 对于贝氏体参阅式(18); C_r为贝氏体延缓生成系数, 该系数值取决于金属中合金的含量。

对于非扩散转变的马氏体组织, 其所占体积分数的函数为:

$\begin{matrix} X_{m} = X_{r} (1 - e^{- α (M_{s} - T)}) (20) \end{matrix}$

式中:X_r为温度降至马氏体转变起始温度时剩余的奥氏体体积分数; 基于热成形钢在低于M_s(马氏体转变起始温度)时, 有90%的X_r转化为马氏体组织的假设, 取α =0.011。

温度对相变的影响函数为:

$\begin{matrix} f (T) = (T_{cr} {- T)}^{n} \exp (- Q_{i} / RT) (21) \end{matrix}$

式中:(T_cr-T)代表过冷度, 而T_cr为各相转变的起始温度; T为当前温度; 对于铁素体和珠光体n值取3, 而对于贝氏体n值取2; Q_i为扩散活化能; R为通用气体常数。

依据合金质量分数试验数据^[14]计算各相转变起始温度的公式为:

$\begin{matrix} \begin{matrix} T_{ferrite} = 1185 + 203 - 203 \sqrt[]{C} - 15.2 Ni + \\ 44.7 Si + 104 V + 31.5 Mo - 30 Mn - \\ 11 Cr - 20 Cu + 700 P + 400 Al + \\ 120 As + 400 T i (22) \\ T_{pearlite} = 996 - 10.7 Mn - 16.9 Ni + 29 Si + \\ 16.9 Cr + 290 As + 6.4 W (23) \\ T_{bainite} = 929 - 58 C - 35 Mn - 75 Si - \\ 15 Ni - 34 Cr - 41 Mo (24) \\ T_{martensite} = 834 - 474 C - 33 Mn - 17 Ni - \\ 17 Cr - 21 Mo (25) \end{matrix} \end{matrix}$

合金元素对各转化相相变速率的影响函数为:

$\begin{matrix} \begin{matrix} f (C_{ferrite}) = (59.6 Mn + 1.4 5 Ni + 67.7 Cr + \\ 244 Mo + K_{f} {B)}^{- 1} (26) \\ f (C_{pearlite}) = {[1.79 + 5.42 (Cr + Mo + \\ 4 MoNi) + K_{p} {B] D}}^{- 1} (27) \\ D = \frac{1}{\exp (- 27500 / RT)} + \frac{0.01 C + 0.52 Mo}{\exp (- 37000 / RT)} (28) \\ f (C_{bainite}) = \\ [10^{- 4} {(2.34 + 10.1 C + 3.8 Cr + 19 Mo)]}^{- 1} (29) \end{matrix} \end{matrix}$

由于相变潜热对结果影响甚微, 故本研究中未考虑相变潜热的释放问题, 本文采用的硼钢相变本构模型中的材料常数如下:G为8; Q_ferrite/R为9300; Q_pearite/R为9412; Q_bainite/R为15093; R为8.3; a为0.011; K_f为1.9e⁵; K_p为3.1e³。

2.2 相变本构模型的验证

采用牛顿迭代法对相变本构模型进行求解, 将不同冷却速率下的数值模拟结果与试验数据进行对比^[15](见表2), 发现所采用的相变分析材料本构模型能够较真实地反映材料相变的结果, 证明该相变本构模型可以用于高强钢热成形有限元分析。

表2 不同冷却速率下的相变数值模拟结果与试验数据对比 Table 2 Comparison of computed and experimental results for phase transformation at different cooling rates

3 基于损伤-相变本构的有限元分析

3.1 用户自定义材料子程序的定义

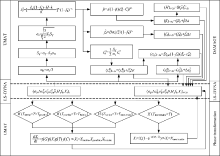
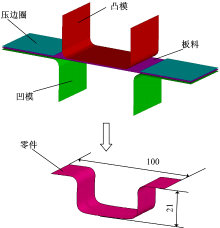
本文利用LS-DYNA软件的用户自定义材料子程序接口编写损伤-相变本构的子程序, 供其求解时调用。图2为该子程序的流程图, 当子程序被调用时, LS-DYNA向子程序传递t时刻各材料点的状态变量(σ _ij, Δ $\begin{matrix} {ε^{T}}_{ij} \end{matrix}$ , $\begin{matrix} {ε^{T}}_{ij} \end{matrix}$ , $\begin{matrix} {ε^{p}}_{ij} \end{matrix}$ , $\begin{matrix} \bar{ρ} \end{matrix}$ , H, f_d, X_i), 所有变量默认初值为0。LS-DYNA在调用子程序时还会向子程序传递时间增量Δ t及当前温度T, 经子程序计算得到t+Δ t时刻各变量的值, 最后将更新后的变量返回到LS-DYNA求解器。

3.2 有限元模型的建立

利用LS-DYNA软件数值模拟2 mm厚的22MnB5高强度钢板热成形过程。模型示意图见图3, 其中板料与模具采用面-面接触, 表面传热系数为3000 W/(m²· K), 忽略板料与空气间的热交换, 板料与模具间的动、静摩擦因数均为0.2, 其他工艺参数见表3。

表3 板料与模具的工艺参数及材料属性 Table 3 Processing parameters of sheet and mould and its material properties

模型中模具均采用刚性物理材料及各向同性材料, 其材料属性见表3。板料采用用户自定义物理材料及各向同性热材料, 其主要热学参数见表4^[16]。模具与板料均采用Belytschko-Tsay壳单元进行模拟。整个计算过程中凹模、压边圈保持静止; 成形阶段凸模向下运动, 成形完成后即保持静止。压边圈与凹模的间隙始终等于板料初始厚度, 即压边圈的作用主要是热传导而非压边。

	Figure Option View Download New Window
	图2 子程序流程图Fig.2 Flow chart of subroutine

	Figure Option View Download New Window
	图3 帽形件模型示意图Fig.3 Schematic diagram of cap-shaped model

3.3 模拟结果的分析

帽形件模型在整个计算时间内完成了冲压成形及保压淬火工艺。通过冲压成形阶段(0~0.14 s)和保压淬火阶段(0.14~8 s)板料上损伤变量及马氏体体积分数变化的历程如图4、图5所示, 证明了研究中采用的损伤-相变本构模型可实现高强钢热成形过程中损伤及相变的预测。

表4 硼钢主要热力学参数 Table 4 Main thermodynamic parameters of boron steel

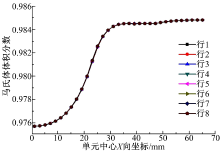
选取1/4的帽形件模型建立简化模型(见图6(a)), 展开后的模型由264个四边形壳单元组成, 其中沿X轴正向为33列、沿Y轴正向为8行, 单元边长均为2 mm(见图6(b))。简化模型沿X轴正向各单元损伤及相变的最终情况如图7、图8所示, 这样仅利用该简化模型, 即可了解整个帽形件模型成形后的损伤及相变情况。

	Figure Option View Download New Window
	图4 损伤变量变化的历程Fig.4 Change course of damage variable

	Figure Option View Download New Window
	图5 马氏体体积分数变化的历程Fig.5 Change course of volume fraction of martensite

	Figure Option View Download New Window
	图6 展开前后的简化模型Fig.6 Simplified model before and after unfolding

	Figure Option View Download New Window
	图7 展开后简化模型上单元的损伤变量值Fig.7 Damage variable of elements on simplified model after unfolding

从图7可以看出, 简化模型中成形损伤主要集中在模型的侧壁及圆角处, 底部及法兰处几乎没有损伤, 而同一列单元的损伤变量值基本相同(由于材料流动略有不同), 最大成形损伤出现在图6中第17列(深色处), 该列大部分单元的损伤值已达到0.7, 说明整个帽形件已失去承载能力。从图8可以看出, 简化模型中同一行单元马氏体体积分数呈现逐渐升高的趋势; 而同一列单元的马氏体体积分数基本相同, 最大马氏体体积分数出现在模型的法兰部位, 最小马氏体体积分数出现在模型底部。整个简化模型的马氏体体积分数均已达到95%以上, 说明整个帽形件的强度已足够。

	Figure Option View Download New Window
	图8 展开后简化模型上单元的马氏体体积分数Fig.8 Volume fraction of martensite of elements on simplified model after unfolding

4 结论

(1)基于损伤力学及微观相变理论, 建立了损伤-相变本构方程。

(2)采用损伤-相变本构方程进行硼钢热成形有限元分析, 不仅可以获得整个成形过程中的相变情况, 还可以直观地看到在载荷作用下板料的损伤过程, 因而可方便地对板料失效进行预测。

(3)利用损伤-相变本构方程对帽形件热成形过程进行有限元分析, 发现最终马氏体体积分数的最大值出现在帽形件的法兰部位, 其均值为98.5%, 而最终成形损伤的最大值则集中在帽形件侧壁的中部, 其值达到了0.7, 表明帽形件已失去承载能力。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Naderi M, Ketabchi M, Abbasi M, et al. Analysis of microstructure and mechanical properties of different high strength carbon steels after hot stamping[J]. Journal of Materials Processing Technology, 2011, 211(6): 1117-1125. [本文引用:1]
[2]	高云凯, 高大威, 余海燕, 等. 汽车用高强度钢热成型技术[J]. 汽车技术, 2010(8): 56-60. Gao Yun-kai, Gao Da-wei, Yu Hai-yan, et al. Analysis on high-strength steel hot forming technology for automobile[J]. Automobile Technology, 2010(8): 56-60. [本文引用:1]
[3]	周靖, 王宝雨, 徐伟力, 等. 耦合损伤的22MnB5变形本构模型[J]. 北京科技大学学报, 2013, 35(11): 1450-1457. Zhou Jing, Wang Bao-yu, Xu Wei-li, et al. Damage-coupled constitutive model of 22MnB5 steel in hot deformation[J]. Journal of University of Science and Technology Beijing, 2013, 35(11): 1450-1457. [本文引用:1]
[4]	Bok H H, Lee M G. Comparative study of the prediction of microstructure and mechanical properties for a hot-stamped B-pillar reinforcing part[J]. International Journal of Mechanical Science, 2011, 53(9): 744-752. [本文引用:1]
[5]	Lee M G, Kim S J. Application of hot press forming process to manufacture an automotive part and its finite element analysis considering phase transformation plasticity[J]. International Journal of Mechanical Science, 2009, 51(11-12): 888-898. [本文引用:1]
[6]	Bariani P F, Bruschi S, Ghiotti A. Advances in predicting damage evolution and fracture occurrence in metal forming operations[J]. Journal of Manufacturing Processes, 2012, 14(4): 495-500. [本文引用:1]
[7]	Malcher L, Mamiya E N. An improved damage evolution law based on continuum damage mechanics and its dependence on both stress triaxiality and the third invariant[J]. International Journal of Plasticity, 2014, 56: 232-261. [本文引用:1]
[8]	Kachanov L M. Time of the rupture process under creep conditions[J]. Izv Akad Nauk SSR Otd Tech Nauk, 1958, 8: 26-31. [本文引用:1]
[9]	Lin J, Liu Y, Dean T A. A review on damage mechanisms, models and calibration methods under various deformation conditions[J]. International Journal of Damage Mechanics, 2005, 14(4): 299-319. [本文引用:1]
[10]	Watt D F, Coon L, Bibby M, et al. An algorithm for modelling microstructural development in weld heat-affected zones(part a)reaction kinetics[J]. Acta Metallurgica, 1988, 36(11): 3029-3035. [本文引用:1]
[11]	马宁, 胡平, 郭威. 热成形硼钢热、力及相变耦合关系[J]. 材料热处理学报, 2010, 31(11): 33-36, 41. Ma Ning, Hu Ping, Guo Wei. Experiments and analysis of relations among heat, stress and transformation of boron steel for hot forming[J]. Transactions of Materials and Heat Treatment, 2010, 31(11): 33-36, 41. [本文引用:1]
[12]	Lin J, Hayhurst D, Dyson B. A new design of uniaxial testpiece with slit extensometer ridges for improved accuracy of strain measurement[J]. International Journal of Mechanical Sciences, 1993, 35(1): 63-78. [本文引用:1]
[13]	Li N, Mohamed M S, Cai J, et al. Experimental and numerical studies on the formability of materials in hot stamping and cold die quenching process[C]∥The 14th International ESAFORM Conference on Material Forming AIP Conf Proc, 2011: 1555-1561. [本文引用:1]
[14]	Akerstrom P, Bergman G, Oldenburg M. Numerical implementation of a constitutive model for simulation of hot stamping[J]. Modelling and Simulation in Materials Science and Engineering, 2007, 15: 105-119. [本文引用:1]
[15]	Naderi M, Saeed-Akbari A, Bleck W. The effects of non-isothermal deformation on martensitic transformation in 22MnB5 steel[J]. Materials Science and Engineering A, 2008, 487(1-2): 445-455. [本文引用:1]
[16]	Arthur Shapiro. Finite element modelling of hot Stamping[J]. Metal Forming, 2011, 80(9): 658-664. [本文引用:1]

2011

0.0

... 0 引言目前高强钢被广泛用于制造车身零部件,这样既减轻了车的质量,又提高了汽车的碰撞安全性^[1] ...

0.0

... 应力场的变化又反作用于温度场,所以热成形工艺本身就是一个热-力-相变耦合的过程^[2],这个过程中,存在着板料成形损伤和微观组织的相变,而二者会影响零件的成形质量和机械性能 ...

2013

0.0

... 针对上述问题,国内外很多学者进行了深入研究^[3,4,5,6,7],Kachanov^[8]通过研究最简单的单轴拉伸脆性损伤破坏,提出损伤演变方程,Lin等^[9]提出一种基于位错硬化的损伤模型,Watt等^[10]预测了焊接过程中微观组织的演变,胡平等^[11]建立了热成形热、力、相变耦合本构关系 ...

2011

0.0

2009

0.0

2012

0.0

2014

0.0

1958

0.0

2005

0.0

1988

0.0

2010

0.0

1993

0.0

... 与Lin等^[12]在推导蠕变变形本构方程时的方法类似,本文采用如下损伤力学本构方程: ...

2011

0.0

... 2 损伤本构模型的验证将不同温度和应变率下的数值模拟结果与硼钢单拉试验结果^[13]进行对比,如图1所示,发现数值模拟结果与试验结果基本一致,证明该损伤本构模型可以用于高强钢热成形有限元分析 ...

2007

0.0

... 依据合金质量分数试验数据^[14]计算各相转变起始温度的公式为: ...

2008

0.0

... 2 相变本构模型的验证采用牛顿迭代法对相变本构模型进行求解,将不同冷却速率下的数值模拟结果与试验数据进行对比^[15](见表2),发现所采用的相变分析材料本构模型能够较真实地反映材料相变的结果,证明该相变本构模型可以用于高强钢热成形有限元分析 ...

2011

0.0

... 板料采用用户自定义物理材料及各向同性热材料,其主要热学参数见表4^[16] ...