作者简介:王鑫(1986-),男,博士研究生.研究方向:RFID加密协议及防碰撞算法.E-mail:buptwxin@gmail.com
针对实际应用环境下某些标签一直滞留在读写器识别范围内的情况,在自适应型查询仲裁协议(AQS)算法基础上,提出一种高效无线射频识别自适应型跟踪树防碰撞算法(HACT)。首先,利用分而治之的方法对滞留标签和新到标签分别进行识别;其次,设计了三叉树碰撞位跟踪算法对新到标签进行识别;最后,提出了合并质询串构建分支树法自适应调整质询队列对滞留标签进行识别,实现了单个质询串对多个标签的识别。理论分析和仿真实验表明HACT算法性能明显优于AQS算法。
Under the environment of practical applications, some tags still stay in the identification range of the reader. Based on the AQS algorithm, a highly efficient Radio Frequency Identification (RFID) adaptive tracking tree anti-collision algorithm is put forward. First, arriving tags and stay tags are identified in the way to divide and conquer. Then, a ternary tree collision tracking algorithm is designed for the arriving tag identification. Finally, a method of merging inquiry string and building branch tree for adaptive adjusting inquiry queue is proposed to identify stay tags, which implements a single inquiry string can identify multiple stay tags. Theoretical analysis and simulation experiments show that the performance of the proposed algorithm is better than that of existing AQS algorithm.
无线射频识别(RFID)技术具有远距离识别、批量读取及可读写等诸多优点。因此, 广泛应用于物流管理、交通运输、航空等重要领域。RFID系统主要由后台数据库、读写器、标签构成, 其通过读写器对贴附在物件上的标签ID识别以实现物件跟踪与管理。读写器在共用信道下利用单双工方式实现标签批量识别, 然而, 当多个标签同时响应必然导致信号混叠, 使其不能正确识别标签, 从而增大了系统识别延时。因此, 设计高效防碰撞算法以提高标签识别效率十分必要。
目前, RFID防碰撞算法主要分为ALOHA和树形算法两类。ALOHA类算法具有操作简单的优点, 当帧长与标签数相等时系统吞吐率最优[1], 然而, 该类算法存在严重的“ 标签饥饿” 现象, 由此导致了标签漏检问题; 树形算法包括QT算法和BS算法两类[2], 该类算法通过制定分类规则不断将相同特征标签归为一个集合。QT算法通过标签对比质询串进行分类。BS算法通过标签逐次产生随机数{0, 1}分类标签碰撞集[3], 直到碰撞集中仅含1个或0个标签。树形算法具有识别精度高的优点, 但存在识别时间较长的问题。文献[4]提出了CT算法, 利用曼切斯特码定位碰撞位并在碰撞位处分割碰撞集, 与QT算法相比消除了空闲时隙并减少了碰撞时隙。针对具有滞留标签的实际应用场景, 文献[5]设计了AQS、ABS算法, 通过保留上一帧识别过程中的叶子节点质询信息进而迅速识别滞留标签。文献[6]提出了CRB及ECRB算法, 避免了滞留标签和新到标签之间的碰撞, 然而由于其基于QT算法, 碰撞时隙和空闲时隙的影响仍然较大。文献[7]提出了SRB和PRB算法, 利用对比读写器ID的方式分别识别滞留标签和新到标签, 然而, 受新到标签识别采用BS算法的影响, 不可避免地受空闲时隙影响及滞留标签离开后再次进入应用场景的影响。文献[8]在PRB基础上提出了RBA, 利用帧号绑定消除了滞留标签再进入场景的问题。同时, ABS/PRB/RBA算法需标签内置随机数产生器及计数器, 对标签具有较高要求。因此, 本文主要研究基于AQS算法的防碰撞算法。
本文针对具有滞留标签的特殊应用环境提出了HACT算法。HACT算法通过标签对比读写器ID及识别帧号的方式对滞留标签和新到标签分而治之地进行识别[6, 8]。进一步通过对标签ID进行进制转换, 并通过“ 放大标识位” 机制定位碰撞位及相应的碰撞情况, 在消除空闲时隙的基础上自适应调整分割叉数对碰撞集进行分割, 进而提高了新到标签识别效率。同时, 提出自适应调整合并质询串构建分支树法对滞留标签进行识别, 标签判断自己在分支树上的位置并在确定时刻仅需响应bit(1)进行签到, 极大地提高了读写器对滞留标签的识别速度并降低了标签耗能。在对新到标签和滞留标签识别效率同时提高的基础上, HACT算法性能较AQS算法得到了较大提高。
本文用到的符号及定义如表1所示。读写器以“ 帧” 为单位识别标签, 即每帧完成对识别范围内所有标签的识别。定义β r, i为fi帧读写器r识别范围内的标签集, Cs、Ca、Cl分别为fi+1帧相对于fi帧的滞留标签、新到标签、离开标签, 则:
| 表1 符号说明及定义 Table 1 Symbols explanation and definition |
HACT算法分两个阶段识别Ca和Cs, 执行流程见流程1~4, 只有标志位满足flag==1的标签响应读写器的质询信号。读写器在每帧初始阶段广播Comd1||RIDr||CurF, 标签接收后与RIDt||TNF进行对比。若相同, 则标签判定自己为滞留标签, 置flag=0; 否则判定自己为新到标签, 置flag=1。因此, 第一阶段仅有Ca的flag==1, 当Ca识别完毕后, 读写器发送Comd2, 标签置flag为~flag, 因此, 在第二阶段仅有Cs响应质询。标签根据合并质询串判断其在分支树上的位置并在准确时刻响应bit(1)进行签到, 读写器循环利用Q中质询串对Cs进行识别, 直到Q==NULL, 当Q==NULL时完成当前帧。由此, HACT算法分阶段分别对Ca和Cs进行识别。以下对Ca识别算法进行阐述。
流程1:读写器总执行流程
1 RanID=排序后的标签ID
2 CurID=NULL
3 CurF=RNF
4 发送Comd1‖ RIDr‖ CurF
5 While NULL≠ Q do
6 if(1=Phase)
7 Phase=1∥执行第1阶段流程
8 end if
9 发送Comd2
10 if Phase=2 & & Q!=NULL
11 q=pop(Q)
12 发送质询串q
/* 检测滞留标签存在性* /
13 QueryR=foreseea TrA
14 for i=1 to length(TrA)
15 if 1=QueryR[i]
16 if 1=foreseeA[i]
17 pop(RanID)
18 push(CurID)
19 end if
20 pop(RanID)
21 end if
22 end if
23 end while
24发送终止帧命令
25 Q=EstQ(CurID)
26 RanID=SortQ(CurID)
27 RNF=RNF+1
流程2:读写器第1阶段执行流程
1 读写器发送质询前缀q, 起始化q=ξ (空字符串
2 while QT!=NULL do
3 q=pop(QT)
4 发送质询前缀q
5 读写器接收信道反馈CF并检测碰撞位
6 if CF==m‖ * 1
7 push(QT, q‖ m‖ 0)
8 push(QT, q‖ m‖ 1)
9 push(QT, q‖ m‖ 2)
10 发送终止信号(编目标签继续传输信号)
11 else if CF==m‖ * &
12 push(QT, q‖ m‖ 0)
13 push(QT, q‖ m‖ 1)
14 发送终止信号(编目标签继续传输信号)
15 else if CF==m‖ 01
16 push(QT, q‖ m‖ 0)
17 push(QT, q‖ m‖ 2)
18 发送终止信号(编目标签继续传输信号)
19 else if CF==m‖ 11
20 push(QT, q‖ m‖ 1)
21 push(QT, q‖ m‖ 2)
22 发送终止信号(编目标签继续传输信号)
23 else if仅仅接收到了一个标签的响应
24 push(CurID)
25 end while
流程3:标签总执行流程
1 接收读写器命令m
2 while Cm!=终止帧命令do
3 if Cm=Comd1& & (RIDr≠ RIDr
4 flag=1; TNF=CurF+1; RIDr≠ RIDr
5 执行第1阶段标签程序
6 else
7 flag=0; TNF=CurF+1; RIDr≠ RIDr
8 end if
9 if Cm=Comd2 then
10 flag=-flag
11 end if
12 if m=query& & 1=flag then
13 根据合并质询判断其在分支树位置
计算准确时刻发送bit(1)
14 endif
15 接收来自于读写器的消息m
16 end while
流程4:标签第1阶段执行流程
/* 接收质询前缀q=q1q2…qs,
标签ID为t1t2…tl* l* /
1 接收读写器质询前缀q
2 while q!=停止发送命令do
3 flag1=1
4 for i=0到i=x进行逐位对比
5 if qi!=ti
6 flag 1=0
7 break
8 end if
9 if flag1=1
10 标签发送txtx+1…tb
检测到停止命令则停止响应
11 end if
12 接收质询前缀q
13 end while
1.2.1 新到标签识别算法
针对Ca识别设计了三叉树碰撞位跟踪算法, 以下进行具体阐述。
首先将标签ID转化为三进制, 设标签ID为b1…bk-1bk, bi∈ {0, 1}, 转化后的ID为t1…tj…tl-1tl, tj∈ {0, 1, 2}, 利用式(2)进行转化, 例如“ 111” 转化为三进制后为“ 21” 。
读写器发送质询串q, 标签执行流程4的1~4行进行逐位对比。因此, ID前缀与q相同的标签发送除q外的三进制标识txtx+1…tl。读写器接收信道反馈后定位碰撞位及碰撞情况并进行相应处理(如流程2中的6~24行), 循环执行该流程直到每个标签集中仅有1个标签, 以下对碰撞位检测及编码方式进行说明。
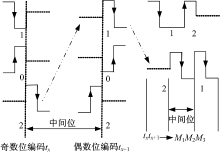
借鉴CT算法碰撞位定位思想提出“ 放大标识位” 编码方式检测碰撞位。如图1所示, 以txtx+1为例进行说明, 虚线表示该位不发送任何信号, 令txtx+1编码后为M1M2M3, 若tx和tx+1为0或1, 则M1和M3如同曼切斯特编码, M2不发送信号; 若tx为2, 则M1不发送信号, 中间位M2为负迁移; 若tx+1为2则M3不发送信号, 中间位M2为正迁移, 这样利用3个传输位对txtx+1进行了编码。
若满足质询条件的标签对自身txtx+1编码并响应, 令读写器接收的信道信号为K1K2K3, 则碰撞检测如图2所示。若K2为副载波信号则K1和K3同时具有状态位2; 若K2为正迁移则K3具有状态位2, K2为负迁移则K1具有状态位2; 若K2检测不到信号则K1和K3都不包含状态位2; K1及K3对状态位的检测类似曼切斯特编码, 利用以上机制可跟踪到碰撞位及碰撞情况。以此类推, 标签及读写器逐两位进行编码和检测碰撞。读写器解码后做如下表示, 将某位的碰撞情况表示为l1l2, l1对应(0, 1)的碰撞情况, 分别用“ * , 0, 1, & ” 表示同时包含0和1、包含状态位0、1、不包含0和1, l2对应状态位2, 分别用“ 1, & ” 表示包含2、不包含2。因此, 位碰撞情况可分类进行表示, 见流程2中6~19行, 同时, 系统对
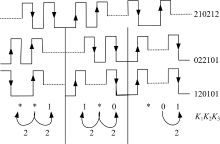
图3为读写器对28个具有10位三进制ID标签的识别过程, 读写器与标签执行第一阶段流程, 同时, 读写器根据碰撞位碰撞情况进行逐次分割, 并根据碰撞时隙将信道反馈信号及对应质询串分别压入队列Q1和Q2。
1.2.2 滞留标签识别算法
由于Ca对Cs的识别无干扰, 在fi+1帧读写器可逐一广播滞留标签ID, 与广播ID相同的标签响应bit(1)以证明其存在性, 然而, 该种方式仅能避免AQS算法空闲时隙的影响并节省标签耗能, 识别耗时仍然较长。提出的合并质询串法则借助读写器保存的fi帧所有识别标签的ID, 将滞留标签规约在确定时隙响应bit(1)进行签到, 实现了一个质询串对多个标签的质询识别, 以下进行具体阐述。
合并质询串法对分支树下标签共有ID前缀进行合并以降低冗余信息传输, 类似于建立析构分支树。分支树上层节点具有下层节点的共有质询串, 如图4所示读写器利用“ 共有质询串||分支||补加串” 的形式构成合并质询串, 其中, 共有质询串对应分支树下所有标签共有前缀, 同时合并质询串对分支树下节点碰撞情况进行说明。标签则根据接收到的合并质询串析构分支树, 利用合并质询串中的碰撞情况说明以确定具体签到时刻。
以下以图3中标签为fi+1帧的滞留标签为例说明Cs识别流程。fi帧完毕后读写器分别利用EstQ(CurID)及SortQ(CurID)建立质询队列Q并对CurID中的标签ID进行排序。如图3所示, 读写器从滞留标签质询树最后一个碰撞节点依据从下到上、从右到左的顺序建立队列Q, 并根据Q对滞留标签进行排序依次压入PreID。读写器利用Q对滞留标签进行识别, 标签则在对应时刻签到, 以证明存在性。
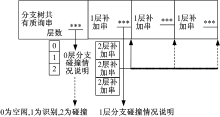
读写器在fi帧结束后对所有识别标签利用流程2在内部建立如图3的识别过程并记录Q1、Q2, 如图5所示, 以Q中第1个质询串为例说明构造及识别过程。首先利用Q1中最后一个质询串20212查找上一层质询串202, 202继续在Q1中查找到2, 进一步在Q1中找出所有首位为2的碰撞质询串并结合Q2构造合并质询串, 利用质询串“ 2” 及Q2中与之唯一对应的“ 0& * 1” 可知“ 20” 为分支树下所有标签共有前缀, “ 20” 下一位为碰撞位, 进而构造“ 20 2 122” , 其中20表示分支树下所有标签共有前缀, 2表示该子树层数, 122说明“ 0层” 的三个节点碰撞情况, 即以200、201、202为质询串的标签集分别对应可识别时隙、碰撞时隙、碰撞时隙。接着构造“ 1层” 质询串与识别情况, 对应于“ 201” 下的时隙为碰撞时隙, 因而, 根据Q1与Q2的对应关系, 以“ 201” 为质询串的标签需补加串“ 011” , 对应分支下为3个可识别时隙, 故识别情况为“ 111” 。以“ 202” 为质询串的质询需补加串“ 1” , 其分支下的3个时隙对应为“ 122” , 为说明标签碰撞情况, 需补加串“ 21” 和“ 011” 。最后, 可得合并质询串Mstr1为202122||011111||1122||21||011||, “ ||” 表示副载波信号, 故标签可分段识别数据串, 202122||011111||1122||中“ ||” 倒数三位为时隙碰撞情况, 依据分支树从上到下、自左而右的顺序读写器可对分支树下标签ID排序并压入PerID。
标签根据Mstr1决定发送bit(1)的时刻。标签根据Mstr1析构分支树, 标签在Mstr1第一个“ ||” 处, 即“ 202122||” 截取后四位判断分支树层数及0层碰撞情况, 因此, 以“ 200” 为前缀的标签对应可识别时隙, 第1时刻传输bit(1); 而“ 201” , “ 202” 对应碰撞时隙, 进一步以“ 201” 为前缀的标签以“ 011111||” 后三位为碰撞情况, “ 011” 为补加串, 即以“ 2011011” 为前缀且后一位为“ 0, 1, 2” 的标签分别在第2, 3, 4时刻发送bit(1)。以202为前缀的标签以“ 1122||” 判断补加串及三分支碰撞情况, 即以“ 20210” 为前缀的标签集和以“ 20211” 为前缀的标签集为碰撞集。由此, 标签继续跟踪其补加串“ 21||” “ 011||” , 即以“ 2021121” 为前缀且后一位为“ 0, 1, 2” 的标签分别在6, 7, 8时刻发送bit(1), 以此类推对分支树进行析构。因此, 按照分支树从上到下、自左向右的顺序滞留标签确定发送bit(1)的时刻。
读写器发送合并质询串后对应检测信道反馈信号TrA, 进而利用foreseeA与TrA将PreID中标签ID删除或压入队列CurID。时刻间隔为bit(1)从标签传输到读写器所需时间。若分支树下标签全部滞留则读写器预见反馈信号为foreseeA={1 1 1 1 1 1 1 1 1 1 1}。某标签存在则在对应时刻反馈bit(1), 若对应时刻无响应则读写器将其记为0, 故TrA={0, 1}length(foreseeA), 由图5可知合并质询串仅对0、1层标签节点碰撞情况进行了说明, 对2层质询时隙碰撞情况没有进行说明。由此, 若原来不存在的标签则在foreseeA中以“ 0” 表示, 因此, 若foreseeA[i]☉TrA[i]为1则第i个标签存在, 将其ID压入CurID, 否则该标签不存在。构造Mstr1后, 在Q1Q2中对应删除该分支树的相关信息, 由此读写器从最后一个碰撞节点利用自右向左、从下到上逐一建立分支树合并质询串, 即每次从最后一个碰撞节点开始建立质询串并将对应分支树下标签ID排序压入PurID, 同时, 标签响应bit(1)后进入Sleep状态。
首先对新到标签识别算法的性能进行分析, 继而给出HACT算法的性能分析。
假设读写器范围内具有n个新到标签, 根据新到标签识别算法, 在碰撞位处自适应采用二叉树或三叉树分割。内部节点对应于碰撞时隙, 叶子节点对应可识别时隙, 故数量为n, 以下分完整三叉树和完整二叉树两种情况进行讨论。
(1) 完整三叉树
结论1:完整三叉树即每个碰撞节点包括3个分支节点。在标签数为n时, 设T3(n)及E3(n)为完整三叉树的总时隙数和吞吐率, 则总时隙数为T3(n)=(3n-1)/2。
证明:用数学归纳法进行证明。
当碰撞节点为1时, T3(n)为4, n=3。故T3(3)=(3× 3-1)/2=4;
当碰撞节点数为k时, 假如命题成立则n=2k+1,
当碰撞节点数为k+1时, 等同与将某个碰撞节点替换为3个可识别标签, 故总时隙数增加了3个, 标签数增加了2个, 因此
进一步可知:
(2)完整二叉树
结论2:完整二叉树, 即每个碰撞节点包括2个分支节点。在标签数为n时, 设T2(n)及E2(n)分别为完整二叉树的总时隙数和吞吐率, 则总时隙数为T2(n)=2n-1。
如同完整三叉树证明, 同理可知:
由于HACT算法中新到标签识别算法根据碰撞情况自适应调整叉数对碰撞集分割, 因此, 若令E(n)为新到标签识别算法吞吐率, 则有:
结论3:标签数量越大, 三叉树相对于二叉树的比例越大。
证明:定义P(1)、P(2)、P(3)分别为n个标签情况下任意一位不发生碰撞的概率、0, 1, 2中任意两个碰撞的概率、同时包含0, 1, 2的概率, 则有:
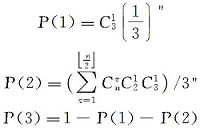
由此可知, 在n{n∈ 2k+1|k∈ (1, 2, …)}个标签的情况下, 则:
若令f(n)=P(3)-P(2), 则有:
对f(n)求导则可知n≥ 3时, f'(n)> 0。故标签数量越大则三叉树比重越大。
HACT算法第二阶段利用合并质询串识别滞留标签, 在大量滞留标签的情况下, 合并质询串对应分支树的层数基本上都为3层, 只有少数质询串对应分支树层数少于3层。因此, 这里将所有分支树统一为3层进行分析。在最坏情况下Q中每个合并质询串可对4个标签进行识别。在最好情况下, 合并质询串对应分支树为完全三叉树, 可以对27个标签进行识别。由此可知, 定义N(Ti+1|Ti)为在fi帧滞留到fi+1帧
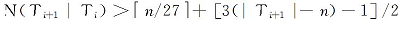
由于n≥ 3时, f'(n)> 0, 且n=4时, f(n)≈ 0。由此可知在n较大的情况下, 滞留标签识别时隙远小于 


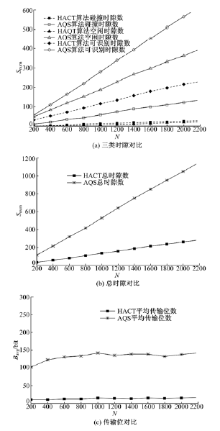
本部分针对AQS算法及HACT算法的性能进行仿真实验对比, 从滞留标签、新到标签的数量及应用环境下标签数量变化对算法性能影响进行仿真实验并分析。以消耗时隙数Snum和标签通信消耗Bavg评估识别算法效率, 主要考虑以下几方面:碰撞时隙及空闲时隙数为无效识别时隙, 浪费了带宽、增大了识别延时; 可识别时隙数:在可识别时隙情况下读写器可确认标签存在性及标签ID; 总时隙数:以上三类时隙数总和; 标签通信消耗:以标签需发送的平均bit数进行衡量, 标签通过电磁耦合供能, 故消耗应尽量低。
设定仿真环境下共有N个标签, 在fi帧读写器识别Mi个标签, 在第fi+1帧通过变化新到率ra和滞留率rs对比算法性能。其中, ra=Ca/(N-Mi), rs=Cs/Mi。以下分两种情况进行仿真实验。
(1)情况1:N=2000, Mi=1000, rs=0.5, ra在0~1区间变化。
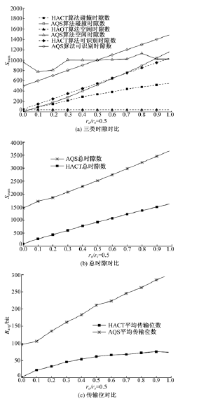
由图6(a)可知HACT算法碰撞时隙数少于AQS算法, 首先是由于HACT算法对Ca和Cs分阶段识别避免了Ca和Cs间的碰撞, 其次, AQS算法Ca越大则Ca与Cs之间的碰撞概率越大, 而HACT算法Ca越大则三叉树比重越大, 故碰撞时隙比例越小, 曲线增长较为平缓。图6(a)中HACT算法与AQS算法相比空闲时隙数极少, 首先由于HACT算法在利用碰撞位跟踪识别新到标签消除了空闲时隙。同时, 对滞留标签识别构成空闲时隙的必要条件是合并质询串对应分支树下标签在fi+1帧同时离开读写器范围, 其次, AQS算法在fi帧为空闲时隙的质询串在fi+1帧进行质询时可能产生新的空闲时隙。同时AQS算法利用QT算法识别Ca也引入了空闲时隙。HACT算法的空闲时隙则由离开标签所致, 因此, 在ra逐渐增加的过程中空闲时隙数保持恒定。图6(a)中HACT算法较AQS算法具有更少的可识别时隙, 其主要是由于HACT算法合并质询串可对分支树下的多个滞留标签进行识别所致。
由图6(b)可知, HACT算法总时隙数远少于AQS算法, 主要是由于碰撞时隙、空闲时隙及可识别时隙均少于AQS算法所致。图6(c)中HACT算法比AQS算法具有更少的标签平均传输位, 总时隙数减少及读写器在检测到碰撞位时终止标签继续传输致使Bavg减少, 同时, 滞留标签仅需响应bit(1)进行签到进一步减少了Bavg。
(2)情况2:N=2000, Mi=1000, ra=0.5, rs在0~1区间变化。
图7(a)中HACT算法碰撞时隙数恒定, 其由于碰撞时隙是由确定数量的Ca所致, 同时, AQS算法随Cs的增加导致Ca与Cs间碰撞概率增大, 故AQS算法碰撞时隙数随Cs的增加而增加。图7(a)中HACT算法相比AQS算法具有极少的空闲时隙, 其主要是由于HACT算法的空闲时隙是由第一阶段合并质询串识别滞留标签所致。进一步HACT算法具有较少的可识别时隙, HACT算法的可识别时隙主要是由识别Ca而产生的, 在Cs个数逐渐增加的过程中, 对Cs的识别采用合并质询串对多个标签进行识别。因此, 由Cs引起的可识别时隙很少。而AQS算法对Cs的识别一个质询串至多可识别一个标签, 因而, 可识别时隙数随rs增大而明显增加。
图7(b)中HACT算法具有更少的总时隙数, 主要是由于合并质询串可识别分支树下的多个滞留标签。图7(c)中HACT算法识别每个标签所用的Bavg少于AQS算法, 其原因类似于情况1中对Bavg减少的分析。
建立如下仿真实验以分析标签数量对算法的影响:共有N个标签分布在10 m× 10 m区域内, 读写器位于区域中心, 识别范围为3 m× 3 m。在连续识别帧之间标签以50%的概率决定是否移动, 移动速度为2 m/s, 进而决定了fi+1帧的滞留标签、新到标签及离开标签。
如图8(a)所示, 随着N的增加, 两种算法的三类时隙数都逐渐增加。HACT算法在N逐渐增大的情况下碰撞时隙增长较为缓慢, 其由于HACT算法消除了Ca与Cs之间的碰撞, 同时, 新到标签识别算法利用碰撞位跟踪法自适应调整二叉、三叉树, 因此, HACT算法的碰撞时隙数较少。同时可见, 在N逐渐增大的情况下, HACT算法相比AQS算法的空闲时隙数极少, 其原因在于HACT算法利用碰撞位跟踪使得对Ca的识别没有空闲时隙, 同时, 对Cs的识别1个合并质询串可识别多个标签也降低了空闲时隙数。最后, HACT算法在N逐渐增大的情况下可识别时隙增加缓慢, 主要是由于1个合并质询串识别多标签所致。
如图8(b)所示, HACT算法的总时隙数较少, 其原因为三类时隙数均少于AQS算法。如图8(c)所示, HACT算法相比AQS算法具有极少的Bavg, 其由于Cs仅需响应bit(1)进行签到。另外, 采用自适应调整叉数的方法极大减少了识别Ca产生的碰撞时隙数, 在检测到碰撞位后终止标签传输信号进一步减少了标签传输位数。
提出一种高效自适应型跟踪防碰撞树算法HACT。该算法通过对滞留标签和新到标签分而治之地进行识别, 避免了二者之间的碰撞, 同时, 对新到标签的识别设计了三叉树碰撞位跟踪算法, 通过“ 放大标识位” 机制使得读写器可精确定位碰撞位的碰撞情况, 进而自适应地调整叉数分割碰撞集, 消除了空闲时隙, 降低了碰撞时隙, 进一步提出合并质询串构建分支树法对滞留标签进行识别, 采用构建分支树与析构分支树实现了单个质询串对多个滞留标签的识别。最后, HACT算法仅需标签进行对比操作即可。通过以上改进机制使得HACT算法在具有滞留标签的应用场景下识别效率高、标签耗能低。因此, HACT算法适用于低价标签快速识别的应用环境。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|