一种基于LDA的<em> k</em>话题增量训练算法

引用本文

辛宇, 杨静, 谢志强. 一种基于LDA的 k话题增量训练算法 . 2015, 45(4): 1242-1252
XIN Yu, YANG Jing, XIE Zhi-qiang. K-topic increment training algorithm based on LDA . Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1242-1252 复制到剪切板

Permissions

一种基于LDA的 k话题增量训练算法

辛宇¹, 杨静¹, 谢志强²

1.哈尔滨工程大学计算机科学与技术学院, 哈尔滨 150001

2.哈尔滨理工大学计算机科学与技术学院, 哈尔滨 150080

杨静(1962-),女,教授, 博士生导师.研究方向:数据与知识工程.E-mail:yangjing@hrbeu.edu.cn

作者简介:辛宇(1987-),男,博士研究生.研究方向:数据与知识工程.E-mail:xinyu@hrbeu.edu.cn

基金:国家自然科学基金项目(61370083, 61073043, 61073041, 61370086); 高等学校博士学科点专项科研基金项目(20112304110011,20122304110012)

摘要

由于LDA模型需要预先给定话题个数 k,因此在进行最优话题个数 k选取时需要对语料库进行 k值循环计算,从而加剧了算法的复杂度。针对LDA模型的最优 k值选取问题,提出LDA话题增量训练算法。该方法首先以词-话题概率熵值作为LDA迭代过程中模糊单词的选取标准,并将抽取模糊单词归入新话题;其次,增加LDA变分推理过程中全局参数 β(单词 -话题概率矩阵)和 α(狄利克雷分布参数)的维数及话题个数 k;再次,将变换后的全局参数 β、 α和 k作为输入进行变分训练;最后,循环调用LDA话题增量训练算法并在似然函数值收敛时停止循环过程,完成 k的增量训练。此外,通过对真实数据集的实验分析验证了本文算法对最优 k值选取的有效性和可行性。

关键词: 人工智能; LDA; 变分推理; 增量训练; 话题分类; 自然语言处理

中图分类号:TP391.4 文献标志码:A 文章编号:1671-5497(2015)04-1242-11

K-topic increment training algorithm based on LDA

XIN Yu¹, YANG Jing¹, XIE Zhi-qiang²

1.College of Computer Science and Technology, Harbin Engineering University, Harbin 150001,China

2.College of Computer Science and Technology, Harbin University of Science and Technology, Harbin 150080,China

Abstract

As the number of topics k should be given in advance in LDA model, therefore, to choose the optimal number of topics k cyclical calculation is needed, which will increases the complexity of the algorithm. To solve the problem of choosing the optimal topics k, the LDA topic increments training algorithm is proposed. First, the entropy of word-topic probability is taken as the extract standard of fuzzy word in the iterative process, and a new topic is generated by the extracted fuzzy word. Second, the dimension of the global parameter β (word-topic probability matrix), dirichlet parameter α, and number of topics k, are increased in the process of variational inference. Third, the variational training algorithm is executed with the transformed global parameters β, α and k. Finally, the LDA topic increment training algorithm is executed cyclically, which is stopped while the likelihood is converged to complete the increment training of k. The effectiveness and feasibility of the proposed algorithm for optimal topics number k is verified by experimental analysis on real datasets.

Keyword: artificial intelltgence; LDA; variational inference; increments training; topic classification; natural language processing

Show Figures

0 引言

LDA(Latent dirichlet allocation, LDA)模型是近些年来话题提取的通用模型^[1]。目前, 话题模型相关的工作大多是对LDA模型进行修改, 或者是将LDA模型作为整个概率模型的一个部件。在LDA模型中, 假设每个文档的主题概率分布服从Dirichlet分布, 并没有对不同主题之间相关性进行刻画。然而, 在真实的语料中, 不同主题之间存在相关性的现象很普遍^[2]。

在面向LDA模型演化研究方面, 2004年, Blei等^[3]提出了主题间为树结构的层级(Hierarchical LDA)。在该模型中, 树中的每个节点代表一个主题, 该模型还有一个特点是可以从语料中估计出主题的个数, 并与使用LDA模型在不同主题数下重复实验得到的最佳主题个数一致。Blei等^{[4, 5]}于2006年又在层级LDA的基础上提出了相关主题模型(Correlated topic model, CTM), 与LDA不同的是, CTM从对数正态分布中对主题概率分布进行采样。Li等^[6]针对CTM只考虑两个主题间关系的不足, 提出了PAM模型(Pachinko allocation model, PAM), 该模型的特点是把主题之间的关系表示成一个有向无环图, 其中叶子节点是单词, 可以看成是由所包含的子节点(主题或单词)构成。之后Mimno等^[7]又在PAM的基础上提出了层级PAM模型, 该模型可以看成是把层级LDA和PAM结合起来, 使得PAM模型中的非叶子节点也具有单词的概率分布。Wang等^[8]向模型中添加了一个作为观测值的时间随机变量后得到了主题随时间变化的主题模型(Topic over time, TOT), 该模型认为主题概率分布受到时间信息的影响, 且时间变量服从beta分布。

在面向上下文信息分析的话题提取方面, 通常主题模型假设单词序列中的单词是可交换的, 即单词的顺序和模型的训练结果无关, 在考虑当前节点和其他节点的关系时, 就破坏了LDA的可交换性假设。Griffiths等^[9]认为可以通过HMM来捕捉句法结构信息, 通过LDA来提示语义关系, 并将两者结合在一起提出了HMM-LDA模型。Wallach^[10]认为语料库生成过程中, 一个单词除了依赖于其对应的主题外还与前一个单词有关, 提出超越词袋(Beyond bag-of-words)的主题模型。张晨逸^[11]等人提出利用MB-LDA进行微博主题挖掘, 该模型在挖掘出微博主题的同时还可挖掘出联系人关注的主题, 并将LDA模型推广到了社交网络中。韩晓晖^[12]等人提出了一种基于LDA的低质量回贴检测方法, 利用检测回贴质量的二元分类性训练SVM分类器, 以区分出质量回贴。

在面向特定任务研究方面, Blei等^[13]针对分类问题提出了有监督LDA模型(Supervised latent dirichlet allocation, sLDA), 该模型将训练语料中的文档类别标记为观测值加入LDA模型, 且类别标号服从一个与文档主题概率分布有关的正态线性分布。Steyvers等^[14]提出作者主题模型(Author topic, AT), 认为每个作者有一个主题概率分布。McCallum等^[15]又在AT模型的基础上, 提出了作者接受者主题模型(Author recipient topic, ART)以判定个人的社会角色。

以上模型的话题个数k均需预先给定, 若要确定最优话题个数k^*则需要循环探测, 其复杂度过高。文献[5]和文献[7]的实验表明, 当k的个数超过某一数据时, k^*的选择开始变得模糊, 导致LDA的最优话题个数选择方法复杂度高且结果不精确。因此, 设计一种高效可行的最优话题个数选择方法是LDA研究的关键问题。本文针对LDA模型的最优k值选取问题, 提出LDA话题增量训练算法, 并通过对真实数据集的实验分析验证了本文算法对最优k值选取的有效性和可行性。

1 LDA模型分析

LDA模型是以单词-话题-参数先验关系构成的3层贝叶斯模型, 三者之间的关系表达模型如图1所示, 其中M为语料库中的文档个数, N为单词表中的单词个数, z_dn为文档d中单词n所属话题的概率, θ _d为文档d中话题z_dn分布的先验参数, α 为语料库中θ 的全局先验参数, β 为k× N单词-话题概率矩阵, 其中k为话题个数, β _i_,_j=p(w=j|z=i)且β _i_,_*=1。根据上述条件概率关系, 文档-单词的数学模型可表示为:

$\begin{matrix} p (w | α, β) = \int p (θ | α) (\overset{N}{\prod_{n = 1}} p (w_{n} | θ, β)) dθ (1) \end{matrix}$

语料库-单词的数学模型可表示为:

$\begin{matrix} p (w | α, β) = \overset{M}{\prod_{d = 1}} \int p (θ_{d} | α) (\overset{N}{\prod_{n = 1}} p (w_{n} | θ, β)) d θ_{d} (2) \end{matrix}$

	Figure Option View Download New Window
	图1 LDA“ 盘子” 模型Fig.1 Plate model of LDA

LDA的生成模型可假设如下:

(1)p(θ |α )~Dir(α )。其表达式为:

$\begin{matrix} p (θ | α) = \frac{Γ (\sum_{i}^{=} α_{i})}{\prod_{i}^{=} Γ (α_{i})} θ_{1}^{α_{1} - 1} \dots θ_{k}^{α_{k} - 1} (3) \end{matrix}$

(2)p(z|θ )~ Multinomial(θ )。

(3)p $\begin{matrix} (w_{n} | z_{n}, β) \end{matrix}$ = $\begin{matrix} β_{z_{n}, w_{n}} \end{matrix}$ .p(w)的条件概率表达式为:

$\begin{matrix} p (w | θ, β) = \sum_{z} p (w | z, β) p (z | θ) (4) \end{matrix}$

根据式(3)(4), 式(2)可表示为:

$\begin{matrix} \begin{matrix} p (w | α, β) = \\ \frac{Γ (\sum_{i} α_{i})}{\prod_{i} Γ (α_{i})} \int (\overset{k}{\prod_{i = 1}} θ_{i}^{α_{i} - 1}) (\overset{N}{\prod_{n = 1}} \overset{k}{\sum_{i = 1}} \overset{V}{\prod_{j = 1}} {(θ_{i} β_{ij})}^{w_{n}^{j}}) dθ (5) \end{matrix} \end{matrix}$

式中: $\begin{matrix} w_{n}^{j} \end{matrix}$ 为编号为n的文件中编号为j单词的出现频数。

加入文档内部估计参数γ 和φ , γ 为β 的文档样本估计值, φ 为文档内部话题的后验概率, φ _i_,_j=p(z=j|w=i)。

假设γ 和φ 相互独立。利用变量β 和z建立文档内部隐含参数的估计模型如下:

$\begin{matrix} q (θ, z | γ, φ) = q (θ | γ) \overset{N}{\prod_{n = 1}} q (z_{n} | φ_{n}) (6) \end{matrix}$

变分推理以极大化单词-话题分布的似然函数p(w|α , β )为目标, 通过在似然函数中加入样本估计参数γ 和φ , 实现对全局参数α 和β 的优化。为此, 式(5)的似然函数表达式如下:

$\begin{matrix} \begin{matrix} logp (w | α, β) = \log \int \sum_{z} p (θ, z, w | α, β) dθ = \\ \log \int \sum_{z} \frac{p (θ, z, w | α, β) q (θ, z)}{q (θ, z)} dθ (7) \end{matrix} \end{matrix}$

2 LDA变分推理过程

2.1 建立变分似然函数表达式模型

$\begin{matrix} \begin{matrix} logp (w | α, β) \geq \\ \int \sum_{z} q (θ, z) logp (θ, z, w | α, β) dθ - \\ \int \sum_{z} q (θ, z) logq (θ, z) dθ = \\ E_{q} [logp (θ, z, w | α, β)] - \\ E_{q} [logq (θ, z)] = L (γ, φ; α, β) (8) \end{matrix} \end{matrix}$

式中:E_q为利用估计参数γ 和φ 计算的期望, 由于Dirichlet分布属于一种指数分布族, 根据文献[1]可知:

$\begin{matrix} \{\begin{matrix} E [\log θ_{i} | α] = Ψ (α_{i}) - Ψ (\sum_{j}^{=} α_{j}) \\ E [\log θ_{i} | γ] = Ψ (γ_{i}) - Ψ (\sum_{j}^{=} γ_{j}) \end{matrix} (9) \end{matrix}$

变分推理的优化过程即寻找L(γ , φ ; α , β )的极值过程。根据式(8)可得:

$\begin{matrix} \begin{matrix} L (γ, φ; α, β) = E_{q} [logp (θ | α)] + \\ E_{q} [logp (z | θ)] + \\ E_{q} [logp (w | z, β)] - E_{q} [logq (θ)] - \\ E_{q} [logq (z)] (10) \end{matrix} \end{matrix}$

根据式(9)可得:

$\begin{matrix} \begin{matrix} L (γ, φ; α, β) = \\ \{logΓ (\sum_{j}^{=} α_{j}) - \overset{k}{\sum_{i = 1}} logΓ (α_{i}) + \\ \overset{k}{\sum_{i = 1}} (α_{i - 1} - 1) (Ψ (γ_{i}) - Ψ (\sum_{j}^{=} γ_{j}))\} + \\ \{\overset{N}{\sum_{n = 1}} \overset{k}{\sum_{i = 1}} φ_{n i} (Ψ (γ_{i}) - Ψ (\sum_{j}^{=} γ_{j}))\} + \\ \{\overset{N}{\sum_{n = 1}} \overset{k}{\sum_{i = 1}} \overset{V}{\sum_{j = 1}} φ_{ni} w_{n}^{j} \log β_{ij}\} - \\ \{logΓ (\sum_{j}^{=} γ_{j}) - \overset{k}{\sum_{i = 1}} logΓ (γ_{i}) + \\ \overset{k}{\sum_{i = 1}} (γ_{i} - 1) (Ψ (γ_{i}) - Ψ (\sum_{j}^{=} γ_{j}))\} - \\ \{\overset{N}{\sum_{n = 1}} \overset{k}{\sum_{i = 1}} φ_{ni} \log φ_{ni}\} (11) \end{matrix} \end{matrix}$

2.2 变分推理参数关系模型

式(11)包含了(α , β , γ , φ )4个参数, 其中 $\begin{matrix} \sum_{i}^{=} \end{matrix}$ φ _ni=1, $\begin{matrix} \sum_{j}^{=} \end{matrix}$ β _ij=1利用拉格朗日乘子法对(α , β , γ , φ )进行优化求值可得到如下结果:

$\begin{matrix} \begin{matrix} L_{[α]} = \overset{M}{\sum_{d = 1}} (logΓ (\sum_{j}^{=} α_{j}) - \overset{k}{\sum_{i = 1}} logΓ (α_{i}) + \\ \overset{k}{\sum_{i = 1}} ((α_{i} - 1) (Ψ (γ_{di}) - Ψ (\sum_{j}^{=} γ_{d_{j}})))) (12) \\ L_{[γ]} = \overset{k}{\sum_{i = 1}} (α_{i - 1} - 1) (Ψ (γ_{i}) - Ψ (\sum_{j}^{=} γ_{j})) + \\ \overset{N}{\sum_{n = 1}} \overset{k}{\sum_{i = 1}} φ_{ni} (Ψ (γ_{i}) - Ψ (\sum_{j}^{=} γ_{j})) - \\ logΓ (\sum_{j}^{=} γ_{j}) + \overset{k}{\sum_{i = 1}} logΓ (γ_{i}) - \\ \overset{k}{\sum_{i = 1}} (γ_{i} - 1) (Ψ (γ_{i}) - Ψ (\sum_{j}^{=} γ_{j})) (13) \\ L_{[β]} = \overset{M}{\sum_{d = 1}} \overset{N_{d}}{\sum_{n = 1}} \overset{k}{\sum_{i = 1}} \overset{V}{\sum_{j = 1}} φ_{ni} w_{dn}^{j} \log β_{ij} + \\ \overset{k}{\sum_{i = 1}} λ_{i} (\sum_{j}^{=} β_{ij} - 1) (14) \end{matrix} \end{matrix}$

$\begin{matrix} w_{n}^{j} \end{matrix}$ 是V维向量, $\begin{matrix} \overset{V}{\sum_{j = 1}} \end{matrix}$ φ _ni $\begin{matrix} w_{n}^{j} \end{matrix}$ logβ _ij=φ _ni $\begin{matrix} \overset{V}{\sum_{j = 1}} \end{matrix} \begin{matrix} w_{n}^{j} \end{matrix}$ logβ _ij=φ _nilogβ _iv, L_[_φ_]表示如下:

$\begin{matrix} \begin{matrix} L_{[φ_{ni}]} = φ_{ni} (Ψ (γ_{i}) - Ψ (\sum_{j}^{=} γ_{j})) + \\ φ_{ni} \log β_{iv} - φ_{ni} \log φ_{ni} + λ_{n} (\sum_{j}^{=} φ_{ni} - 1) (15) \end{matrix} \end{matrix}$

式(12)~(15)分别对(α , β , γ , φ )求零值导数可得到(α , β , γ , φ )的极值关系式如下:

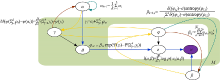
$\begin{matrix} \begin{matrix} M (Ψ (\sum_{j}^{=} α_{j}) - Ψ (α_{i})) = \\ \overset{M}{\sum_{d = 1}} Ψ (\sum_{j}^{=} γ_{j}) - Ψ (γ_{i}) (16) \\ γ_{i} = α_{i} + \sum_{n}^{=} φ_{ni} (17) \\ β_{ij} \propto \overset{M}{\sum_{d = 1}} \overset{N_{d}}{\sum_{n = 1}} φ_{dni} w_{dn}^{j} (18) \\ φ_{ni} \propto β_{iv} \exp (Ψ (γ_{i}) - Ψ (\sum_{j}^{=} γ_{j})) (19) \end{matrix} \end{matrix}$

2.3 变分推理运行过程

根据式(16)~(19)变分推理的参数训练过程分为文档内部参数循环训练过程(训练γ , φ )和语料库总体参数训练过程(训练α , β )。文档内部参数循环训练过程是语料库总体参数过程的子过程。图2为训练过程的盘子模型图, 其中黄色箭头线表示文档内部参数训练过程, 参数γ , φ 根据式(17)和(19)以α , β 为参数进行循环迭代以优化参数γ , φ ; 棕色箭头表示语料库总体参数训练过程, 在语料库内所有文档完成对参数γ , φ 的训练后, 根据式(16)和(18)调整全局参数α , β ; 蓝色箭头表示LDA模型的似然函数的计算过程。

	Figure Option View Download New Window
	图2 LDA变分推理过程Fig.2 Variational inference process of LDA

3 变分推理优化改进策略

LDA话题提取存在两方面问题需要改进:

(1)由于LDA算法在初始运行时需要人为给定话题个数k(较小的整数), k与最佳话题个数k^*的偏离度决定了LDA话题发现的质量, 若k< k^*会导致话题训练的欠拟合, 若k> k^*会导致话题训练的过拟合, 如何选择k值是LDA话题发现尚未解决的问题。

(2)LDA在样本的训练过程中缺少对β 中“ 模糊单词” (即话题归属不确定的单词)的处理, 导致β 矩阵中各话题间的模糊化, 并使得后续的训练结果出现相似的话题结果, 影响话题分类的有效性。

为说明以上两方面问题, 本文统计了CNN网站中的50组话题, 建立了50个样本话题, 并在每组话题中选择词频最高的5个名词作为样本话题词汇, 如表1所示。随机选择2~5组样本话题构成文档, 并以1000个随机文档为单位, 建立40组语料库。

表1 CNN 50个话题的概率表 Table 1 50-topics Probability Table of CNN

topic	word	P	topic	word	P	topic	word	P	topic	word	P	topic	word	P
polity	government prefecture secretary congress parliament	0.244 0.275 0.084 0.182 0.211	makeup	nutritious repair solvent proof gentle	0.194 0.040 0.317 0.255 0.192	bug	ant bee beetle fly spider	0.214 0.305 0.087 0.377 0.014	nature	cave hole mountain hill forest	0.046 0.264 0.243 0.187 0.258	wedding	ceremony anniversary bride pastor groom	0.156 0.351 0.027 0.363 0.100
city	capital slums building museum highway	0.351 0.202 0.143 0.084 0.217	traffic	light milestone stop cross blocked	0.293 0.135 0.189 0.234 0.146	diet	nutrition glutton banquet dessert soup	0.176 0.217 0.265 0.199 0.141	direction	centre corner place spot side	0.172 0.319 0.144 0.056 0.307	vegetable	eggplant turnip potato tomato cabbage	0.355 0.230 0.165 0.029 0.219
family	stock family nephew brother caste	0.150 0.262 0.130 0.157 0.299	company	office colleague affairs sales research	0.288 0.084 0.305 0.033 0.288	weather	mist hail hurricane sunlight breeze	0.252 0.239 0.083 0.210 0.213	agriculture	farm wheat corn cotton village	0.101 0.254 0.231 0.156 0.255	climate	rainfall smog drought volcanoes desert	0.220 0.152 0.219 0.177 0.230
media	news topicality advertisement tabloid singer	0.240 0.212 0.278 0.218 0.049	position	clerk manager supervisor assistant cashier	0.191 0.250 0.193 0.136 0.2289	commodity	comb bag purse watch rug	0.172 0.171 0.088 0.258 0.310	industry	factory works machine electricity workshop	0.249 0.176 0.042 0.219 0.312	wildlife	zebra giraffe panda lion bear	0.342 0.131 0.159 0.202 0.164
religion	chapel Christianity cathedral priest Puritanism	0.141 0.244 0.141 0.243 0.228	bank	account deposit receipt cheque exchange	0.283 0.110 0.206 0.229 0.175	tool	screw saw fork bolt scissors	0.269 0.226 0.212 0.233 0.057	metal	silver gold steel iron brass	0.329 0.252 0.025 0.179 0.213	bird	hawk pigeon penguin swallow sparrow	0.210 0.257 0.346 0.122 0.063
art	exhibition romanticism expressionism naturalism masterpiece	0.113 0.414 0.166 0.260 0.045	music	tempo album classics dance grave	0.185 0.288 0.106 0.148 0.270	facility	hospital clinic shop market hotel	0.208 0.154 0.199 0.219 0.218	building	house tower garden mansion temple	0.332 0.074 0.041 0.416 0.135	fish	carp sardine codfish shark tummy	0.188 0.227 0.260 0.182 0.141
color	pink brown camel green scarlet	0.232 0.268 0.123 0.215 0.160	body	head tongue shoulder back rib	0.013 0.443 0.230 0.027 0.285	profession	actor teacher writer farmer doctor	0.289 0.008 0.082 0.259 0.360	school	subject lecture grade curriculum major	0.065 0.443 0.080 0.360 0.049	time	day season year month century	0.284 0.288 0.289 0.039 0.097
flower	azalea cactus daisy plant lily	0.221 0.171 0.226 0.317 0.063	sport	badminton tennis boxing soccer gymnastics	0.211 0.184 0.233 0.108 0.262	economy	investment check allowance cash share	0.129 0.421 0.161 0.035 0.252	book	manual notebook dictionary textbook library	0.013 0.270 0.194 0.216 0.305	astronomy	universe space planet star satellite	0.255 0.197 0.254 0.183 0.109
costume	wardrobe suit uniform jacket coat	0.242 0.170 0.246 0.130 0.209	tree	pine birch bamboo oak willow	0.236 0.182 0.026 0.305 0.249	law	draft abolish legal judge attorney	0.268 0.180 0.368 0.023 0.160	stationery	pen ink ruler rubber paper	0.265 0.097 0.143 0.215 0.277	war	battle struggle position accident victory	0.355 0.230 0.165 0.029 0.219
kitchen	kettle fridge microwave pot fry	0.151 0.121 0.469 0.255 0.002	cattle	horse goat mouse rabbit bull	0.209 0.279 0.357 0.006 0.147	literature	poetry essay verse prose novel	0.044 0.270 0.367 0.094 0.223	vehicle	car bus ship train plane	0.127 0.381 0.004 0.163 0.323	sentiment	anxious confidence courage like frustrate	0.156 0.351 0.027 0.363 0.100

表1 CNN 50个话题的概率表 Table 1 50-topics Probability Table of CNN

3.1 likelihood值分析

本文对40组语料库建立10~70个话题的LDA跟踪运算, 所得的likelihood值如图3所示, 其中横坐标为话题个数, 纵坐标为likelihood值。由于本文所建立的40组语料库是50个话题的混合, 因此理想状态下50个话题的likelihood值应为极值, 且50个话题的各每组样本likelihood值的偏差应该较小。但图3所示的结果说明LDA算法在话题个数大于40时, 出现likelihood值的模糊化, 无法根据likelihood值判断最优话题个数k^*。

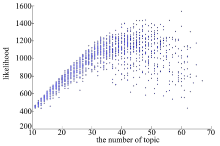	Figure Option View Download New Window
	图3 表1数据集likelihood值(话题个数为10~70)Fig.3 Likelihood of the datasets in table 1 (the number of topics are 10~70)

3.2 β 矩阵分析

本文对第1、8、15、22、29、36组语料库LDA训练后的β 值进行分析, 由于表1数据集中属于同一话题的单词编号邻近, 因此属于同一话题的单词在β 矩阵的位置邻近, 可将β 矩阵元素中的最大值进行聚类以分析LDA的分类效果。β 矩阵的聚类轮廓图如图4所示, 其中x轴为话题号, y轴为单词号。由于表1数据集中各样本话题单词无重复, 因此理想状态下β 矩阵聚类轮廓图的每行每列仅有一个话题聚类簇, 从图4中可直观看到语料库中第1、8、15、22组数据的LDA分析结果较差。

另外, 图4中LDA算法所挖掘出的编号相邻的话题相似度较大, 且有效识别个数最多为40(语料库36)。为了提高LDA的话题精度, 降低话题间的相似度, 本文提出LDA话题增量训练算法, 在提高话题分类精度的同时增量挖掘优化话题个数k^*。

	Figure Option View Download New Window
	图4 语料库1, 8, 15, 22的β 矩阵分析结果Fig.4 β matrix of corpus 1, 8, 15, 22

3.3 LDA话题增量训练算法

变分推理的执行过程中, 以文档内部话题-单词的后验概率φ 作为α 和β 训练的中间变量φ _i_,_j=p(z=j|w=i), 若话题个数为k(k< k^*, k^*为最优话题个数), 必存在某一单词的话题不确定度较高, 即φ _i_,_*的熵值entropy(φ _i_,_*)较大, 其中某一单词w_i的熵值表达式为:

$\begin{matrix} entropy (φ_{i, \cdot}) = - \overset{k}{\sum_{j = 1}} φ_{i, j} \log (φ_{i, j}) (20) \end{matrix}$

entropy(φ _i_,_*)是对单词w_i的不确定性度量, entropy(φ _i_,_*)越大则w_i的不确定性越高, 当前的k个话题对w_i的划分越不合理。此时, 可提取entropy值较大的单词重新组合为一个新的话题, 并复用之前的迭代结果。由于话题的增加需要进行一次语料库总体参数训练(增加参数α 和β 的维数), 为此LDA话题增量训练算法对参数α 和β 的修改如下:

(1)增加β 矩阵的维数。引入熵的阈值参数σ , 选择entropy(φ _i_,_*)大于σ 的w_i构成新的话题, 并将新话题按熵值归一化, 加入β 矩阵。

β _k+_1,_i= $\begin{matrix} \frac{δ ((φ_{i, j}) - σ) entropy (φ_{i, j})}{\sum_{j}^{N} δ ((φ_{i, j}) - σ) entropy (φ_{i, j})} \end{matrix}$ ,

其中 $\begin{matrix} \{\begin{matrix} 0 \\ 1 \end{matrix} \end{matrix} \begin{matrix} \begin{matrix} , δ ((φ_{i, j}) - σ) \leq 0 \\ , δ ((φ_{i, j}) - σ) > 0 \end{matrix} \end{matrix}$

(2)增加α 的维数。以新的β 和α 作为初始参数执行新一次迭代。

α _k+₁= $\begin{matrix} \frac{1}{k} \end{matrix} \begin{matrix} \overset{k}{\sum_{i = 1}} \end{matrix}$ α _i, k=k+1.

在LDA的执行过程中, 迭代次数越高参数β 和α 的训练越充分, 为防止LDA话题增量训练算法在β 和α 尚未充分训练的条件下进行φ 的熵值选择, 导致LDA训练不充分而影响话题发现质量, 需要在LDA迭代过程中加入迭代参数c, 每进行c次迭代时执行一次LDA话题增量训练算法。

图5为LDA话题增量训练算法的参数训练过程, 其中绿色箭头为LDA话题增量训练算法对α 和β 的增量训练过程。

	Figure Option View Download New Window
	图5 LDA话题增量训练算法的参数训练过程Fig.5 Training process of the LDA topic incremental training algorithm

具体的算法描述如下:

功能:利用LDA话题增量训练算法对训练最优话题个数k^*

输入:初始话题个数k

输出:最优话题个数k^*及语料库参数α 和β

count=0;

k^*=k;

repeat

initialize $\begin{matrix} φ_{ni}^{0} \end{matrix}$ :=1/k^*for all i and n

initialize γ _i:=α _i+N/k^* for all i

for every document

repeat

for n=1 to n

for i=1 to k^*

$\begin{matrix} φ_{ni}^{t + 1} \end{matrix}$ := $\begin{matrix} β_{i w_{n}} \end{matrix}$ exp $\begin{matrix} (Ψ (γ_{i}^{t})) \end{matrix}$ ;

end for

normalize $\begin{matrix} φ_{ni}^{t + 1} \end{matrix}$ to sum to 1;

$\begin{matrix} γ_{}^{t + 1} \end{matrix}$ :=α + $\begin{matrix} \sum_{n}^{=} \end{matrix} \begin{matrix} φ_{n}^{t + 1} \end{matrix}$ ;

until convergence

β _ij=β _ij+ $\begin{matrix} \overset{M}{\sum_{d = 1}} \end{matrix} \begin{matrix} \overset{N_{d}}{\sum_{n = 1}} \end{matrix}$ φ _dni $\begin{matrix} w_{dn}^{j} \end{matrix}$ ;

end for

α = newton_raphson(γ ^t+1); //using the newton_raphson method

β =mnormalize(β );

count=count+1;

if count == c

α _k+1= $\begin{matrix} \frac{1}{k^{*}} \end{matrix} \begin{matrix} \overset{k^{*}}{\sum_{i = 1}} \end{matrix}$ α _i;

β _{k+1, i}=δ $\begin{matrix} ((φ_{i, j}) - σ) \end{matrix}$ entropy $\begin{matrix} (φ_{i, j}) \end{matrix}$ /

$\begin{matrix} \sum_{j}^{n} \end{matrix}$ δ $\begin{matrix} ((φ_{i, j}) - σ) \end{matrix}$ entropy $\begin{matrix} (φ_{i, j}) \end{matrix}$ ;

k^*=k^*+1;

count=0;

end if

until convergence(likelihood)

4 实验分析

4.1 CNN数据集分析

图6为语料库13的LDA迭代跟踪过程(语料库13共进行57次迭代), 从中可以直观发现LDA算法对66~70号单词“ makeup” 话题的识别较差, 其原因在于LDA迭代过程中未能在β 矩阵中提取“ makeup” 话题, 使得“ makeup” 单词的话题隶属度相对模糊, 影响了β 后序训练过程中对“ makeup” 话题的识别。

本文利用大量模拟实验验证了LDA话题增量训练算法参数的有效范围分别为σ =(0~1.6), c=(3~12), 并在4.3节分析了参数σ 和c的最优取值问题, 图7为利用本文LDA话题增量训练算法(以10为初始k值, σ =0.3, c=5)对语料库13的增量迭代过程, 该图直观显示了话题个数从10增量训练到50的过程中, 话题间的独立逐渐增强, 相比于图6中LDA话题增量训练算法更趋于理想状态。

	Figure Option View Download New Window
	图6 语料库13的LDA迭代跟踪过程Fig.6 LDA iterative tracking process of corpus 13

	Figure Option View Download New Window
	图7 语料库13的LDA跟踪过程Fig.7 LDA tracking process of corpus 13

图8为40组语料库在本文算法下的likelihood值(以10为初始值, σ =0.3, c=5), 该图显示了本文算法的最佳话题发现个数集中在40~50之间。

	Figure Option View Download New Window
	图8 表1数据集LDA话题增量训练算法下的likelihood值Fig.8 Likelihood of the dataset in Table 1 by the LDA topic increments training algorithm

4.2 真实数据集对比

在数据集的选择方面, 本文采用有明确文档分类的数据集, 以分析本文算法对话题个数选取的有效性, 本文分别选取了自然语言处理中常用的3组数据集, 各数据集的介绍如下:

(1)所选择的数据库包括第36届加拿大国会记事录Aligned Hansards of the 36th Parliament

of Canada(AHPC) a卷(共40个议案)和b卷(共40个议案), 总单词量约为1 300 000个。将每个议案的章节作为LDA分析的“ 文档” , 由于同一议案趋近于同一话题, 因此该数据集的理想话题个数均为40。

(2)兰卡斯特新闻书籍语料库The Lancaster Newsbooks Corpus, 本文算法取其中25类(500本书)书籍为数据集, 以每本书的摘要作LDA分析的“ 文档” , 由于同一类书籍的新闻话题近似, 因此该数据集的理想话题个数为25。

(3)路透社经典文档分类语料库Reuters 21578 Classic text categorization corpus (共50类), 以每本书的摘要作LDA分析的“ 文档” , 该数据集已将各文档进行了分类, 因此该数据集的理想话题个数为50。

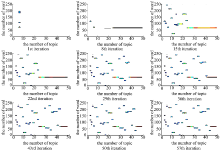
本文算法对上述数据分别利用LDA和LDA话题增量训练算法(σ =0.3, c=5)进行40次实验, 其对比结果如图9所示, 其中蓝色为LDA算法的分析结果, 红色为本文算法的分析结果, 从结果可直观判断本文算法的likelihood高于LDA算法, 验证了本文算法的话题分类合理性高于LDA算法。在话题个数识别方面, 各组数据的话题个数分别为40、45、23、55, 接近于理想话题个数。

	Figure Option View Download New Window
	图9 4种语料库likelihood对比图Fig.9 Comparison chart of 4 corpuses

4.3 参数σ 和c分析

本文利用LDA话题增量训练算法对第36届加拿大国会记事录Aligned Hansards of the 36th Parliament of Canada(AHPC)a卷(共40个议案)作为数据集进行200次迭代, 每次迭代进行15次实验, 其中参数分别为σ =(0.1∶ 0.1∶ 1.5), c=5, 每次将话题个数收敛于38~42的结果判定为正确(共有1036次正确分类), 其统计直方图如图10(a)所示。以AHPC数据集进行200次迭代, 每次迭代进行8次实验, 其中参数分别为σ =0.3, c=(3∶ 1∶ 10), 每次将话题个数收敛于38~42的结果判定为正确(共有966次正确分类), 其统计直方图如图10(b)所示。通过图10(a)与(b)的分析可知:当σ > 1.5时分类的趋于无效, 且c的最优取值区间为(3, 10)。图11为AHPC的三维stem图, 其中LDA话题增量训练算法的最优值为σ =0.45, c=6。

	Figure Option View Download New Window
	图10 AHPC数据集统计直方图Fig.10 Histogram of AHPC dataset

	Figure Option View Download New Window
	图11 AHPC的三维stem图Fig.11 3D stem figure of AHPC

5 结论

本文利用LDA话题增量训练算法, 创新采用以单词-话题概率熵值作为LDA迭代过程中模糊单词选择标准, 将所选择模糊单词归入新的话题优化LDA的迭代过程, 以提高话题独立性为手段提高各单词的合理化分类; 所提出的LDA话题增量训练算法可在实现LDA话题分类优化的同时对最优话题个数k进行增量训练, 最后通过实验对比验证了本文算法在话题分类合理度likelihood与k自动选择方面的优越性, 对深入研究话题分类模型具有一定的理论和实际意义。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Blei D M, Ng A Y, Jordan M I. Latent dirichlet allocation[J]. Journal of Machine Learning Research, 2003, 3: 993-1022. [本文引用:1]
[2]	徐戈, 王厚峰. 自然语言处理中主题模型的发展[J]. 计算机学报, 2011, 34(8): 1423-1436. Xu Ge, Wang Hou-feng. The development of topic models in natural language processing[J]. Chinese Journal of Computers, 2011, 34(8): 1423-1436. [本文引用:1]
[3]	Blei D M, Griffitchs T L, Jordan M I, et al. Hierarchical topic models and the nested Chinese restaurant process[C]∥Advances in Neural Information Processing Systems 16. Cambridge, MA: MIT Press, 2004: 17-24. [本文引用:1]
[4]	Blei D M, Lafferty J D. Correlated topic models[C]∥Advances in Neural Information Processing Systems 18. Cambridge, MA: MIT Press, 2006. [本文引用:1]
[5]	Blei D, Lafferty J. A correlated topic model of science[J]. Annals of Applied Statistics, 2007, 1(1): 17-35. [本文引用:1]
[6]	Li W, McCallum A. Pachinko allocation: DAG-structured mixture models of topic correlations[C]∥Proceeding of the ICML. Pittsburgh, Pennsylvania, USA, 2006: 577-584. [本文引用:1]
[7]	Mimno D, Li W, McCallum A. Mixtures of hierarchical topics with pachinko allocation[C]∥Proceeding of the ICML. Corvllis, Oregon, USA, 2007: 633-640. [本文引用:1]
[8]	Wang X, McCallum A. Topics over time : a non-markov continuous-time model of topical trends[C]∥Proceeding of the Conference on Knowledge Discovery and Data Mining (KDD). Philadelphia, USA, 2006: 113-120. [本文引用:1]
[9]	Griffiths T L, Steyvers M, Blei D M, et al. Integrating topics and syntax[C]∥Advances in Neural Information Processing Systems 18. Vancouver , Canada, 2004. [本文引用:1]
[10]	Wallach H. Topic modeling: beyond bag-of-words[C]∥Proceeding of the 23rd International Conference on Machine Learning. Pittsburgh, Pennsylvania, 2006: 977-984. [本文引用:1]
[11]	张晨逸, 孙建伶, 丁轶群. 基于MB-LDA模型的微博主题挖掘[J]. 计算机研究与发展, 2011, 48(10): 1795-1802. Zhang Chen-yi, Sun Jian-ling, Ding Yi-qun. Topic mining for microblog based on MB-LDA model[J]. Journal of Computer Research and Development, 2011, 48(10): 1795-1802. [本文引用:1]
[12]	韩晓晖, 马军, 邵海敏, 等. 一种基于LDA的Web论坛低质量回贴检测方法[J]. 计算机研究与发展, 2012, 49(9): 1937-1946. Han Xiao-hui, Ma Jun, Shao Hai-min, et al. An LDA based approach to detect the low-quality reply posts in web forums[J]. Journal of Computer Research and Development, 2012, 49(9): 1937-1946. [本文引用:1]
[13]	Blei D M, McAuliffe J. Supervised topic models[C]∥Advances in Neural Information Processing Systems (NIPS). Vancouver, Canada, 2008. [本文引用:1]
[14]	Steyvers M, Smyth P, Rosen-Zvi M, et al. Probabilistic author-topic models for information discovery[C]∥Proceedings of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Seattle, Washington, 2004: 306-315. [本文引用:1]
[15]	McCallum A, Corrada-Emmanuel A, Wang X. The author recipient-topic model for topic and role discovery in social networks: experiments with enron and academic email[R]. Technical Report UM-CS-2004-096, 2004. [本文引用:1]

2003

0.0

... 0 引言LDA(Latent dirichlet allocation,LDA)模型是近些年来话题提取的通用模型^[1] ...

2011

0.0

... 然而,在真实的语料中,不同主题之间存在相关性的现象很普遍^[2] ...

2004

0.0

... 在面向LDA模型演化研究方面,2004年,Blei等^[3]提出了主题间为树结构的层级(Hierarchical LDA) ...

2006

0.0

... Blei等^[4,5]于2006年又在层级LDA的基础上提出了相关主题模型(Correlated topic model,CTM),与LDA不同的是,CTM从对数正态分布中对主题概率分布进行采样 ...

2007

0.0

... Blei等^[4,5]于2006年又在层级LDA的基础上提出了相关主题模型(Correlated topic model,CTM),与LDA不同的是,CTM从对数正态分布中对主题概率分布进行采样 ...

2006

0.0

... Li等^[6]针对CTM只考虑两个主题间关系的不足,提出了PAM模型(Pachinko allocation model,PAM),该模型的特点是把主题之间的关系表示成一个有向无环图,其中叶子节点是单词,可以看成是由所包含的子节点(主题或单词)构成 ...

2007

0.0

... 之后Mimno等^[7]又在PAM的基础上提出了层级PAM模型,该模型可以看成是把层级LDA和PAM结合起来,使得PAM模型中的非叶子节点也具有单词的概率分布 ...

2006

0.0

... Wang等^[8]向模型中添加了一个作为观测值的时间随机变量后得到了主题随时间变化的主题模型(Topic over time,TOT),该模型认为主题概率分布受到时间信息的影响,且时间变量服从beta分布 ...

2004

0.0

... Griffiths等^[9]认为可以通过HMM来捕捉句法结构信息,通过LDA来提示语义关系,并将两者结合在一起提出了HMM-LDA模型 ...

2006

0.0

... Wallach^[10]认为语料库生成过程中,一个单词除了依赖于其对应的主题外还与前一个单词有关,提出超越词袋(Beyond bag-of-words)的主题模型 ...

2011

0.0

. 2011, 48(10):1795-1802

Topic mining for microblog based on MB-LDA model

基于MB-LDA模型的微博主题挖掘

Zhang Chen-yi , Sun Jian-ling , Ding Yi-qun.

张晨逸, 孙建伶, 丁轶群

1(College of Computer Science and Technology, Zhejiang University, Hangzhou 310027)2(Industrial Technology Research Institute of Zhejiang University, Hangzhou 310027)

As microblog grows more popular, services like Twitter have become information providers on a web scale. Early work on microblog focused more on its user relationship and community structure, without considering the value of content. So the research on microblog requires a change from solely user’s relationship analysis to its content mining. Although traditional text mining methods have been studied well, no algorithm is designed specially for microblog data, which contain structured information on social network besides plain text. In this paper, we propose a novel probabilistic generative model based on LDA, called MB-LDA, which is suitable to model the microblog data and takes both contact relation and document relation into consideration to help topic mining in microblog. We present a Gibbs sampling implementation for inference of our model, and find not only the topics of microblog, but also the topics focused by contactors according to the final results. Besides, our model can be extended to many texts associated with social networking such as E-mails and forum posts. Experimental results on actual dataset show that MB-LDA model can offer an effective solution to topic mining for microblog.

随着微博的日趋流行,Twitter等微博网站已成为海量信息的发布体,对微博的研究也需要从单一的用户关系分析向微博本身内容的挖掘进行转变.在数据挖掘领域,尽管传统文本的主题挖掘已经得到了广泛的研究,但对于微博这种特殊的文本,因其本身带有一些结构化的社会网络方面的信息,传统的文本挖掘算法不能很好地对它进行建模.提出了一个基于LDA的微博生成模型MB-LDA,综合考虑了微博的联系人关联关系和文本关联关系,来辅助进行微博的主题挖掘.采用吉布斯抽样法对模型进行推导,不仅能挖掘出微博的主题,还能挖掘出联系人关注的主题.此外,模型还能推广到许多带有社交网络性质的文本中.在真实数据集上的实验表明,MB-LDA模型能有效地对微博进行主题挖掘.

... 张晨逸^[11]等人提出利用MB-LDA进行微博主题挖掘,该模型在挖掘出微博主题的同时还可挖掘出联系人关注的主题,并将LDA模型推广到了社交网络中 ...

2012

0.0

. 2012, 49(9):1937-1946

An LDA based approach to detect the low-quality reply posts in web forums

一种基于LDA的Web论坛低质量回贴检测方法

Han Xiao-hui , Ma Jun , Shao Hai-min

韩晓晖, 马军, 邵海敏

(School of Computer Science and Technology, Shandong University, Jinan 250101)

Web forum is one of the major types of social media in Web 2.0. However, the generated contents in Web forums can vary in quality, ranging from excellent detailed opinions to topic drift contents or swear words. Therefore, a novel LDA (latent Dirichlet allocation) based approach is proposed in this paper to detect low-quality posts in Web forums. Compared with previous methods, the new one uses both semantic and statistic features of a post to evaluate its quality. The semantic features include JunkInsignificant (JI) topic proportion, topic uncertainty and topic relevance, which are computed in LDA topic space in order to overcome the ineffectiveness of TF·IDF based features in short texts. An LDA model is firstly built to predict the topic distribution of each post. Then, semantic features of a post are computed based on its topic distribution. The statistic features contain surface, syntactic and forum specific features of posts, which are selected based on the analysis of the posts contents. Since detecting the low-quality posts can be considered as a bi-classification problem, SVM is used to filter the low-quality posts. Experimental results on three different datasets show that the new approach outperforms the previous ones in terms of precision, recall and F\-1 values.

为了过滤Web论坛中的低质量回帖,提出了一种新的基于LDA(latent Dirichlet allocation)的低质量回帖检测方法.不同于以往的方法,该方法在对回帖进行质量分类时使用了两类特征:语义特征和统计特征.提出并定义了垃圾非重要(JI)主题比例、主题不确定度和主题相关度3种语义特征.为克服TF·IDF方法在表示稀疏文本语义上的局限性,语义特征在LDA主题空间上计算.另外,统计特征包括浅层特征、句法特征和论坛专有特征.由于检测回帖质量可被看作二元分类问题,训练SVM分类器来区分出低质量回帖.在3个不同数据集上的实验结果表明,新方法在精确率、查全率和F\-1测度上均优于已知的方法.

... 韩晓晖^[12]等人提出了一种基于LDA的低质量回贴检测方法,利用检测回贴质量的二元分类性训练SVM分类器,以区分出质量回贴 ...

2008

0.0

... 在面向特定任务研究方面,Blei等^[13]针对分类问题提出了有监督LDA模型(Supervised latent dirichlet allocation,sLDA),该模型将训练语料中的文档类别标记为观测值加入LDA模型,且类别标号服从一个与文档主题概率分布有关的正态线性分布 ...

2004

0.0

... Steyvers等^[14]提出作者主题模型(Author topic,AT),认为每个作者有一个主题概率分布 ...

2004

0.0

... McCallum等^[15]又在AT模型的基础上,提出了作者接受者主题模型(Author recipient topic,ART)以判定个人的社会角色 ...