建立分子对接任务结点集P{P₀, P₁, …, P_j, …}, 其中P₀为执行当前分子对接任务的源结点, P₁, P₂, …是可作为分子对接任务迁移的目的结点机。

为了衡量结点本身事件的频率和强度的变化, 采用中断事件出现次数的数学期望值和均方差来进行量化比较, 并得出可靠性因子, 将其加入到任务迁移策略的考虑因素之中。

结点机P_j∈ P在执行任务T_i的过程中, 若共有S(S≥ 0, S∈ I)次中断, 则任务T_i在结点P_j的执行时间为A_ij=X₁+Y₁+X₂+Y₂+…+X_s+Y_s+X_s+1。其中, X_i代表子任务的计算时间, Y_i代表源结点本身用于自身事务执行的中断时间。令ω =X₁+X₂+…+X_s+X_s+1, 则ω 代表分子对接任务自身在P_j结点所需要的计算时间。

结点计算安全性的判定基于如下两种假设:

(1)分子对接任务应被分配到负载较轻的结点上。

(2)结点本身的任务到达次数符合泊松分布。

利用如上假设及M/G/1排队系统相关理论^[16], 可以得到如下命题:

命题:结点的任务符合排队系统M/G/1, 中断时间到达率为λ , 分子对接任务自身所需要的计算时间为ω , 则结点自身的中断事件的发生符合参数为λ * ω 泊松分布。

其概率表述如下:

Ps=PrS=s=(λω)se-λωs!1

根据上述命题, 结点P_j自身中断事件发生次数的数学期望值计算如下:

EkTi=EETi|S=Eω+Y1+Y2+…+Ys|S=Eω+S* EY1=ω1+λEY1=11-ρω2

式中:ρ 表示结点P_j的利用率。结点P_j自身中断事件发生次数的方差计算如下:

σkTi=EσTi|S+σETi|S=ES* σY1+σω+S* EY1=λ* ω* σY1+λ* ω* E2Y1=λ* ω* EY12=ρ(θ2+1)(1-ρ)3×μω3

式中:θ 为服务参数; μ 为服务接受率参数。在M/G/1队列系统中, 可令θ =1, 则式(3)化简为:

σkTi=2ρ(1-ρ)3μω4

令可靠性因子R_{k, i}为结点自身中断事件发生次数的数学期望和方差的二元函数, 即任务T_i在结点P_j上的即时可靠性因子可表示为:R_{k, i}=φ (E_k(T_i), σ _k(T_i)), 且E_k(T_i)、σ _k(T_i)越大, 则R_{k, i}值越大。

当结点P_j的利用率参数ρ =0, 即对任意一个任务T_i, 根据式(2)(4)可得出其数学期望值E_k(T_i)=ω , 方差σ _k(T_i)=0时, 该结点可靠性取得最优值, 即R_{k, i}=0。

综合考虑各候选结点的可靠性因子和网络拥塞因素, 提出了迁移目标结点机的选取算法, 如算法1所示。

算法1 迁移目标结点机选取算法

Function Node_Selection(P, T, R₀, ε )

输入:P是结点机集合; T是分子对接任务集合; R₀是源结点的可靠性因子; ε 为考虑网络拥塞等因素的差值。

输出:通过判断任务T_i在结点P_j上的即时可靠性因子R_{k, i}以及结点P_j自身中断事件发生次数的数学期望E_k(T_i), 得到目标结点机。

{

result=P0;

R[j]← 1;

For all j∈ P do

{

For all i∈ T do

{

计算任务T_i在结点P_j上的即时可靠性因子R_{k, i};

计算结点P_j自身中断事件发生次数的数学期望E_k(T_i);

}

}

For (j=1, j< =n, i++)

{

If R_j为结点集P-{P₀}中可靠性最好(可靠性因子值最小)的结点 and R_j≤ R₀-ε

Result=P_j;

}

Return Result;

}

对任意结点P_j∈ P{P₀, P₁, …, P_j, …}, 计算其可靠因子。当同时满足如下两个条件时, 向结点P_j执行任务迁移。

条件1:R_{k, i}为结点集P-{P₀}中可靠性最好(可靠性因子值最小)的结点。

条件2:R_{k, i}≤ R_{k, 0}-ε ; 其中, R_{k, 0}为源结点的可靠性因子, ε 为考虑网络拥塞等因素的差值。

在药物筛选过程中, 借助计算机辅助药物分子设计软件, 可以减少用于实验环节的候选小分子集合, 大大缩短成药时间。其中, 药物分子对接软件(如:DOCK), 通过考虑与大分子对接过程中所产生的能量值, 对可能成药的小分子进行筛选。具体做法是借助能量打分值进行综合评判, 能量值越低则成药的可能性越大。通常, 对接结果将返回所有小分子按照能量从低到高的排序集合。结合实际经验, 在进行分子对接动态迁移过程中, 考虑迁移效率, 对完成对接的小分子集合, 可根据实际情况进行设置, 比如:选取能量值较低的前20%作为目标小分子集合。根据分子对接这一特点, 在数据迁移之前, 对已完成对接的小分子、正在对接的小分子和未进行对接的小分子, 分别考虑数据迁移。动态迁移算法如算法2所示。

算法2 药物分子对接动态迁移算法.

Function DynamicMigration(P₀, CurrenLigandNumber, TotalNumber)

输入:源结点机编号P₀, 当前正在对接的小分子编号CurrenLigandNumber, 总共需要对接的小分子数TotalNumber;

输出:目标小分子集合Result[SequenceNo, LigandNo, EnergyScore], SequenceNo是能量值序号, LigandNo为小分子编号, EnergyScore为对接产生的能量打分值;

{

P_j=Node_Selection(P, T, R₀, ε ); //确定迁移目标结点机

Num=getNumberofligand(CurrenLigandNumber); //获取循环次数, 可根据需要设置

For (i=1; i< =Num; i++ )

Result[SequenceNo, LigandNo, EnergyScore]=getLigand(DockingResultSet); //从当前对接结果中, 经过能量排序得到能量值较低的小分子集合

NumberofDocking=TotalNumber-CurrenLigandNu-

mber; //目前未对接的小分子数

Increment=100; //增量单位

IncrementalDataMigration(P₀, P_j, Increment, NumberofDocking, bestLigandNo); //按照小分子编号顺序迁移, 每次传递数量为Increment

Copy the CPU and memory status for the current ligand; //暂停源虚拟机, 同步脏内存页以及当前CPU状态等

Restart P_j and run docking from CurrenLigandNumber to the last ligand; //启动目标结点P_j的对接程序

Rank the EnergyScore to get the final ligand result set; //通过比较, 得到最终目标小分子集合

Return(Result) ;

}

具体动态迁移过程分为如下6阶段:

(1)确定目标结点

根据迁移目标结点机的选取算法, 综合考虑可靠性因子和网络拥塞情况, 得到目标结点机。

(2)传递中间结果

针对已经完成对接的小分子集合, 仅对能量值排序位于前20%的目标小分子集合实施在线迁移, 传递其小分子编号及能量信息, 这就避免了复杂的信息传送。

(3)增量数据预迁移

对于未对接的小分子, 首先根据编号得知未对接小分子数量, 将未对接小分子总数传送到目的主机, 再按照编号顺序实施增量式迁移。增量单位通常为10, 即一次迁移100个小分子, 避免因大量数据同步而造成停机时间过长。

(4)停机拷贝

针对正在进行对接的小分子, 实施停机迁移, 暂停源虚拟机, 同步脏内存页以及当前CPU状态等。

(5)目标结点对接执行

按照恢复后的状态启动对接程序, 继续完成计算任务。

(6)得到对接结果

目标结点对接完成后, 通过比较能量打分值, 得到最终目标小分子集合。

通过算法1, 能够选取最优的迁移目标机, 之后再借助算法2, 完成了药物分子对接任务的动态任务迁移, 这就保证了迁移后, 计算任务能够继续在目标机执行, 并结合源结点的计算结果, 得到最终的目标小分子集合。

硬件环境:7台在不同子网的宿主机结点, 结点间带宽设置为100 MB/s, 包括一台源结点机P₀, 配置为Xeon E5504 CPU, 8 GB RAM, 任务迁移目的机包括6台PC机:P₁, P₂, P₃, P₄, P₅, P₆, 配置均为Xeon E5504 CPU, 4 GB RAM。搭建了局域网环境下的网格平台, 共3个子网, 子网1中有P₀和P₁, 子网2中有P₂, P₃, P₄, 子网3中有P₅和P₆, 子网之间通过千兆交换机连接。

软件环境:KVM宿主机软件环境为Ubutun Server 10.04 TLS, 内核版本2.6.32-24, KVM版本kvm-88, 分子对接软件为DOCK6.2, 参数使用默认值。

实验选择的受体:选取环氧合酶-2作为受体, 它的PDB编号是4COX, 其大分子结构如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 环氧合酶-2受体大分子Fig.1 An Enzyme Called Cyclooxygenase-2 receptor

实验使用的配体小分子库:配体小分子库中有1177个小分子。

结点性能因素:受体为环氧合酶-2时, 对接花费时间在0.1 s至12 s范围内。如果只在P₀运行对接程序, 对接执行10次的平均时间为206 375 s。如果只在P₁至P₆运行对接程序, 对接执行10次的平均时间为247 788 s。从以上结果可以看出, 当任务从P₀向目标结点(P₁至P₆)中的某个结点进行迁移时, 因结点性能因素, 对接执行的总体时间会增加约20%。

如果没有特别指出, 同一组应用负载下迁移实验重复10次, 本节中实验结果为10次结果的平均值。

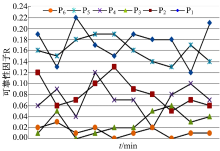
每一组迁移实验中, 当P₀计算结点对接计算任务执行到100 000 s左右, 环氧合酶-2受体分子对接执行到第563号配体小分子时, 对结点P₀进行大量磁盘I/O操作, 从而导致其降低性能至临界值, 触发迁移。各目标结点的可靠性因子变化趋势如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 目标结点的可靠性因子变化趋势Fig.2 Trends of reliability factors of the target hosts

从图2可以看出, P₆结点的方差(抖动性)最小, 表示结点负载相对稳定, 同时数学期望值最小, 表示该结点负载较轻。受各目标结点负载及性能影响, 从源结点向各个目标结点的迁移时间及在目标结点对接小分子库中剩余的小分子的时间各不相同, 具体时间花销如表1所示。

表1

Table 1

表1(Table 1)

表1 目标结点迁移时间和对接时间 Table 1 Migration and docking time of the target hosts 结点 编号 迁移时间 /s 对接时间 /s 在目标结点总体 花费时间/s P1 157.2 130 442.2 130 599.4 P2 132.4 128 379.1 128 511.5 P3 113.9 123 745.8 123 859.7 P4 126.7 126 477.2 126 603.9 P5 129.5 129 687.4 129 816.9 P6 97.2 120 724.6 120 821.8

表1 目标结点迁移时间和对接时间 Table 1 Migration and docking time of the target hosts

综合比较可靠性因子取值及变化趋势, 选择P₆结点作为目标结点实施在线迁移。在线迁移过程, 向P₆结点传递目标小分子集合, 包括小分子编号及其能量值以及未对接小分子数量, 并同步内存页及CPU状态, 按照增量方式传递小分子数据, 重新启动分子对接过程。其中, 迁移所用时间为97.2 s, 迁移后, 目标计算机能够正确完成计算任务, 所用时间为120 724.6 s。这样, 利用在线迁移技术, 在P₀和P₆所花费对接时间, 再加上迁移所用时间为220 821.8 s。对接花费时间与目标机器单独计算花费时间接近, 总体计算效率可以接受, 并确保了分子对接计算的安全性。

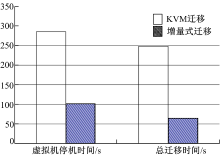
实验的最后, 我们对比了实施增量式迁移前后的迁移性能, 包括总迁移时间以及虚拟机停机时间, 实验结果如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 总迁移时间和停机时间对比Fig.3 The comparison of total migration and shutdown time

从图3中不难看出, 实施增量式迁移之后大幅度缩短了迁移的总体时间。采用增量式迁移在对小分子数据实施迁移时, 由于分子对接过程具有按照小分子编号顺序对接的特点, 因此以增量的方式将最近使用的小分子最早传递给目标结点, 使对接过程及早启动并持续执行, 大大提高了迁移时间。增量式迁移方式比KVM迁移平均复制数据页的迭代收敛速率高, 在停机时脏页面数较少。相反, KVM迁移机制在停机时需要复制更多的脏页面数, 因此停机时间稍长, 大约为286 ms, 大于增量式迁移中的101 ms平均时间。

通过上述对比可以看出, 在总体迁移时间和虚拟机停机时间方面, 运用在线增量式迁移机制进行药物分子对接迁移效率明显提升。