引用本文
杨艳林, 靖晶, 杨志杰, 许天福, 王福刚. 多相流数值模拟中复杂地质体网格剖分实现技术. 2015, 45(4): 1281-1287
YANG Yan-lin, JING Jing, YANG Zhi-jie, XU Tian-fu, WANG Fu-gang. Grid subdivision technology for multiphase flow simulation with complex geological condition. Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1281-1287  
Permissions
Copyright©2015, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
多相流数值模拟中复杂地质体网格剖分实现技术
杨艳林, 靖晶, 杨志杰, 许天福, 王福刚
吉林大学 地下水资源与环境教育部重点实验室,长春 130021
王福刚(1975-),男,教授.研究方向:水文地质与环境地质.E-mail:wangfugang@jlu.edu.cn

作者简介:杨艳林(1984-),男,博士研究生.研究方向:多相流多组分数值模拟与程序开发.E-mail:yangyanlinjida@gmail.com

基金:中国地质调查局工作项目(12120113006300)
摘要

考虑到复杂地质体的网格化剖分建模技术对多相流体数值模拟精准度的影响,提出了基于布点法构建任意多边形、任意约束的PEBI(Perpendicular bisection)多约束、交互式网格剖分实现技术与网格生成算法。网格生成过程包括五个方面:布点;三角剖分;查找不合格三角形,调整点布局;生成泰森多边;进行拓扑重构,生成二维、三维PEBI网格。剖分过程中将直井、水平井、断层等各种约束分别概化为点、线、区约束,基于泰森多边形的拓扑重构,完成PEBI网格的生成。将剖分算法耦合到作者前期开发的可视化建模软件TOUGHVISUAL上,并应用于几种典型复杂情况下地质体网格剖分建模,应用结果显示了本文方法的科学实用性和操作简便性。

关键词: 计算机应用; PEBI网格; 布点方法; 三角剖分
中图分类号:TP391,P641 文献标志码:A 文章编号:1671-5497(2015)04-1281-07
Grid subdivision technology for multiphase flow simulation with complex geological condition
YANG Yan-lin, JING Jing, YANG Zhi-jie, XU Tian-fu, WANG Fu-gang
Key Laboratory of Groundwater Resources and Environment,Ministry of Education, Jilin University, Changchun 130021,China
Abstract

Under complex geological condition, grid subdivision technology influences the accuracy of multiphase flow simulation. To meet the need of grid subdivision for multiphase flow simulation, a new algorithm is proposed to construct Perpendicular Bisection (PEBI) mesh of arbitrary shape with any constraints. This proposed algorithm for generating 2D and 3D PEBI grid includes five steps, e.g. point layout, triangle subdivision, unqualified triangles identification and point layout adjustment, Thiessen polygon generation, and topology reconstruction. In this process, various constraints (vertical wells, horizontal wells and faults) are reduced to point constraints, line constraints and area constraints, respectively. To provide a flexible way of arranging the point location, several common methods were expounded. The PEBI grid was created base on Thiessen polygon topology reconstruction. The proposed algorithm was applied to PEBI grid generation of several typical complicated geological conditions. The results demonstrate the feasible, simple and flexible characteristics of the proposed algorithm.

Keyword: computer application; PEBI grid; distribution approach; triangular subdivision
0 引 言

多相流体广泛存在于地下能源和资源开发以及废物地质处置等多个领域[1], 如油藏开采、深部地热能开发、核废料地质处置、二氧化碳地质储存等多个科学领域都涉及到气相、液相、固相等多物理场耦合的科学问题。多相流数值模拟技术已经成为研究这些领域科学问题的重要工具, 并得到了广泛应用。在数值模拟中, 对于复杂地质体的剖分建模技术一直以来都是影响数值模拟精准度的一个重要因素, 不同的网格剖分方法对计算规模、计算结果产生很大影响。在多相流数值模拟领域, 目前对于复杂地质体(如断层、井周围地质体)的剖分建模技术仍存在很大不足。本文基于前人的研究基础, 提出了基于布点法构建任意多边形、任意约束的PEBI(Perpendicular bisection)多约束、交互式网格剖分实现技术与网格生成算法, 有效解决了复杂地质体难以客观刻画的科学问题。

1 PEBI网格

在地质体网格剖分方法中, 结构化网格作为最简单的空间离散方法, 应用广泛, 但在描述复杂地质条件时存在两方面局限:①不能很好的反映复杂边界情况, 尤其是在处理井周围和断层等地质体时, 结构化网格处理效果很不理想(见图1); 凌建军等[2]采用矩形网格来逼近任意形状的边界, 但仍有较大的误差; ②存在不可忽略的网格取向效应, 而且不利于网格加密。为了解决这一问题, 有的学者[3, 4]提出将PEBI网格应用到多相流模拟中。PEBI网格是一种非结构网格, 利用了有限元划分网格的灵活性, 可以逼近任意油藏形状, 便于网格加密; 同时, PEBI网格中相邻网格块的交界面垂直平分相应PEBI网格的连线, 具有有限差分的剖分特点, 最终得到的差分方程与笛卡尔差分方程相似, 从而可更好地逼近流体流动形态, 以获得更加精确的数值解。

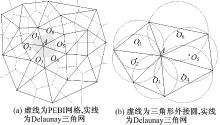
图1 规则网格与PEBI网格Fig.1 Regular grid and PEBI grid

PEBI网格是一种局部正交网格, 即任意两个相邻网格块的交界面一定垂直平分相应PEBI网格节点的连线。国外学者在这方面做了大量的工作, Heinemann等[3]首次将PEBI网格应用到油藏模拟中, 其后Palagi等[4]也将PEBI网格运用到实际油藏数值模型中, 获得了满意的效果。国内在这方面的研究与应用虽起步较晚, 但至今也取得了丰富的成果, 向祖平等[5]先按点搜索的方法生成三角网, 后再生成其对偶图, 连接其外接圆心生成PEBI网格(见图2); 蔡强等[6]运用控制圆法生成了带约束的PEBI网格; 查文舒等[7]根据井间流线方程的特征, 提出了井间干扰条件下的PEBI网格划分算法。王星等[8]利用PEBI网格分别对多分支水平井井型优化进行研究; 刘立明等[9]基于精细油藏数值模拟中出现的问题, 提出了径向网格和PEBI网格的混合PEBI算法; 王代刚等[10]提出了基于前沿推进的改进型PEBI网格生成方法。

综合目前的PEBI网格生成算法, 其自动化程度较高, 没有或较少有人工参与方面的生成方法, 不利于研究者对具有多约束复杂边界地质体的网格剖分。基于这种不足, 本文利用可视化界面的交互式特点, 提出运用交互式布点的方法来生成复杂地质条件下的PEBI网格, 其算法简单, 操作灵活、方便, 可解决多相流模拟中复杂地质体的空间网格离散问题。自动化PEBI网格剖分技术的关键是剖分节点的生成, 本文算法首先对研究区进行合理布点, 并进行Delaunay[11]三角剖分, 追踪其对应的泰森多边形[12], 后分配高程, 生成具有拓扑结构的PEBI网格。

图2 PEBI网格模型Fig.2 Model of PEBI grid

2 网格生成中的约束条件

在复杂的地质体网格剖分中, 模拟区的非均质性、几何形态(边界断层、地层尖灭等)的精细描述、岩石和流体物理性质的空间变化等都要求进行特殊的处理。本文将其综合分成三类, 概化为点、线、区等约束条件, 如直井, 可处理为点约束; 水平井、断层, 可处理为线约束; 其他一些具有区域性的约束则可处理为区约束。下文针对点、线、区约束, 提供了一些布点方法, 以达到事半功倍的效果。对于线约束, 需要网格沿着折线分布, 不允许出现跨过约束线的网格(见图3); 同时网格的单元尺寸和形状也需要做一定的控制, 比如在井眼周围, 为了准确地反映井眼周围流体流动特征, 网格单元由小到大成放射状分布。

图3 两种情况下的PEBI网格Fig.3 PEBI grid in both cases

3 布点方法

为了生成满足几何区域和数值条件要求的高质量网格, 在网格点的布置过程中, 节点的生成以及约束点的生成, 需充分考虑给定几何区域的形状和大小、求解区域中解的变化情况和最终形成网格单元的质量, 以获得高质量高效率的数值模拟网格。

3.1 布点原则

模拟区布置的点将作为生成PEBI网格的单元点(见图4), 点布置得合理与否将直接影响数学模型的求解计算规模、运算时间与解的精度[13]。所以, 在进行网格剖分时需要注意以下几方面问题:

(1)确定合适的布点密度。在多相流(油藏)数值模拟中经常碰到单元网格应剖分得如何细致才能获得合理结果的问题。当然, 在模型运算前是很难回答这个问题的。一般的做法是先执行一个认为合理的网格密度进行试算, 同时对于关键区域(如注入井)进行双倍的网格加密, 重新分析, 并比较两个模型结果。若结果几乎相同, 则网格剖分合理。若两次结果相差显著, 则应继续细化网格直到两次获得近似相等的结果。

(2)单元形状与类型的选择。剖分单元形状可以是三角形、四边形以及其他多边形。剖分形状尽量是正多边形, 这样的计算精度更好些。同时也要考虑单元大小的过渡, 如在加密区域, 单元从稀到疏的逐渐过渡(见图3)。

(3)网格方向(如井处的网格成放射状)与流体的流动方向尽量保持一致。这样的网格剖分更能反应流体流动特征, 以提高计算精度。反之, 则很容易在换算时, 由于计算机的计算精度而引入误差, 误差会在计算过程中传递下去, 越来越大, 使计算结果失真。

图4 各种约束的布点方式Fig.4 Way of distribution point for different constraints

3.2 布点方法

综合考虑实际布点的需要, 本文主要讨论了几种常用的布点方法, 如矩形布点法、环形布点法和推进布点法等。矩形布点主要是在给定的多边形内生成矩形分布点, 最后生成的PEBI单元也是矩形的。环形布点法是主要针对点约束而进行处理的一种方法, 其生成的点环形向外扩散, 以达到生成的PEBI网格方向与径向流动方向相一致。推进布点法则主要用于处理多边形布点, 其在向内推进时, 分布的点会少于前一次的点, 反之, 向外则增加(见图4)。当然也可以先进行多边形自动三角剖分, 后进行PEBI网格划分, 这方面的参考文献较多, 如丁永祥[14]完成的自动三角剖分。

4 生成PEBI网格算法

布点完成后, 接下来需要进行三方面的工作:Delaunay三角剖分; 查找边界钝角三角形, 调整点布局; 生成PEBI, 以完成高质量PEBI网格生成。

4.1 Delaunay三角剖分

Delaunay三角剖分[11]于1934年被提出, 在数学、地理、工程等许多领域应用广泛。目前常用的有逐点插入法、三角网生长法和分割合并法。插入点算法的步骤是:首先, 定义一个包含所有节点的初始网格, 最简单的情形是单个三角形; 向网格中插入一个节点, 找出其外接圆包含此节点的所有三角形, 删除这些单元形成一个包含插入节点的空腔; 将该插入节点与空腔的每条边相连, 形成新的三角形单元; 上述的节点插入过程重复进行, 直到全部节点插入完毕。

4.2 边界钝角三角形

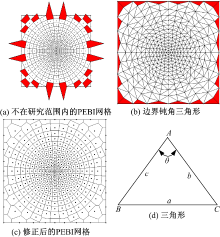
网格剖分若出现钝角三角形, 将直接影响PEBI的网格质量, 从而影响模型的计算精度。在边界上的钝角三角形会产生不在研究范围内的PEBI网格, 如图5(a)所示, 出现这种情况必须调整边界上的点的位置, 直至生成所有PEBI单元都在研究范围内(见图5(c))。边界钝角三角形的查找算法可根据余弦定理来进行判定。

由余弦定理可得角A(见图5(d))的余弦值, 见式(1)(其中a、b、c为边的长度):

cosA=a2+b2-c22ab1

若余弦值等于零, 则为直角三角形, 小于零则为钝角三角形。基于此原理, 可以很容易找到边界钝角三角形(见图5(b))。

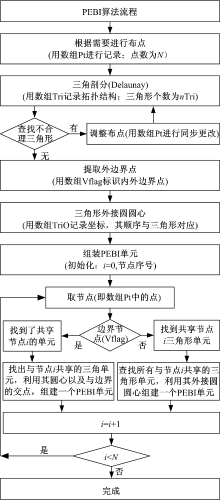
图5 PEBI网格剖分与修正Fig.5 PEBI grid subdivision and revision

4.3 PEBI网格生成

泰森多边形又叫冯洛诺伊图[14](Voronoi diagram), 其应用广泛, 如北京的鸟巢设计就借鉴了泰森多边形的思想, 其原理是先求出每个三角形的外接圆圆心, 后连接圆心, 即可生成泰森多边形, 即PEBI网格。Atsuyuki等[15]、Brassel[16]、向祖平等[5]、蔡强等[6]、刘少华等[17]都对这方面进行过研究。但是为了生成多相流(油藏)数值模拟可运行的网格以及三维空间离散, 还需进行泰森多边形的拓扑重构, 其主要是基于查找共享三角形节点的PEBI单元来构建其拓扑结构, 如图2中角点A周围的O1、O2、O3、O4、O5、O6等组成的单元号。PEBI网格生成流程如图6所示。

图6 PEBI网格生成流程图Fig.6 Flow chart of PEBI grid generation

5 剖分实例与应用
5.1 剖分实例

为了验证本文网格剖分方法的科学实用性, 将算法耦合到作者前期开发的可视化建模软件TOUGHVISUAL[18]平台上进行测试。

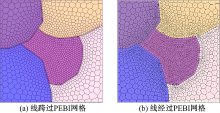
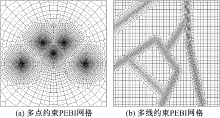
图7 多点/线约束PEBI网格生成Fig.7 PEBI grid generation under multi-point/line constrains

图7(a)为多井点约束(井网很密), 流场存在相互干扰情况下PEBI网格剖分结果, 点周围为径向网格, 其他区域的网格为变尺度的网格。其特点是:距点约束(井)越远, 网格的尺度越大。区域中的3个约束点(丼)的径向区域出现重叠, 此时为了反映流动特征与真实的流动相一致, 采用了干扰网格划分, 其他区域采用非干扰PEBI网格划分。在布点时, 应确定多点约束之间是否存在流场干扰, 然后, 在算法耦合的图形界面上通过人机交互的控制方式进行网格剖分。

图7(b)为多线约束(如水平井与断层交织等复杂情况)时采用多边形与矩形混合的PEBI网格剖分结果。线约束区采用矩形网格, 向外网格逐渐变稀, 之后通过多边形网格与约束区外矩形网格进行连接。约束区外剖分单元也可以是多边形, 在布点时, 可以灵活控制。

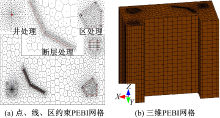
图8(a)是一个点约束、一个线约束、二个区约束情况下的网格划分结果。点约束区的网格剖分, 从点约束处向外网格单元面积逐渐增大, 以减缓数值计算时点约束区各物理场的变量梯度急剧变化的问题; 线约束处强制要求单元不穿过线, 并且单元密度从线约束处向外逐渐增大, 以适应线约束区向外的突变情况; 区约束采用了两种方式的网格单元类型, 一种为矩形, 如图8(a)中的右上部分, 另一种为多边形网格单元, 且单元密度由密到稀分布。这与点的布置直接相关。图8(b)是通过组建相应的二维网格拓扑结构, 分配高程后生成的三维PEBI网格结果。

图8 点、线、区约束PEBI网格生成Fig.8 PEBI grid generation under point, line and area constraints

5.2 应用

二氧化碳地质储存是当今研究的热点问题之一。油气藏是很好的二氧化碳地质储存场地, 同时注入的二氧化碳可提高石油采收率[19]。本文以油田某一区块地质条件网格剖分建模为实例, 进行了本文方法的应用。研究区为一背斜构造, 在注入井约500 m处有一断层。图9为运用本文方法进行网格剖分的过程, 图10为模拟区最后的网格剖分结果, 图11为模拟计算的压力场分布图。

由图10可知, 采用此种网格剖分方法, 可以较好地反映地层和断层的空间分布情况, 证明了本文方法的有效性与正确性。由图11可知, 500 m处的断层对压力场的重新分布产生了较大影响, 符合实际情况。

图9 研究区三角网剖分示意图Fig.9 Triangle mesh subdivision in the study area

图10 研究区PEBI网格生成Fig.10 PEBI grid generation in study area

图11 压力分布图Fig.11 Pressure distribution

6 结束语

复杂地质体的剖分建模技术是影响数值模拟结果的重要环节, 不同的网格处理方式, 将直接影响计算稳定性、复杂程度和计算效率等。本文通过研究多相流数值模拟网格剖分的特点, 提出复杂地质体网格剖分建模的技术和算法, 并将该算法耦合到作者前期开发的多相流可视化建模界面软件TOUGHVISUAL上, 为复杂地质体客观、快速建模提供了技术实现, 为深部能源和资源开发、核废料与二氧化碳等废物地质储存中的多物理场多相流数值模拟提供了科学实用的工具。

The authors have declared that no competing interests exist.

参考文献
[1] 国丽萍, 刘承婷, 刘保君. 石油工程多相流体力学[M]. 北京: 中国石化出版社, 2011. [本文引用:1]
[2] 凌建军, 吴敬轩. 网格方向性对水驱油油藏数值模拟结果的影响[J]. 江汉石油学院学报, 1990, 12(1): 40-45.
Ling Jian-jun, Wu Jing-xuan. The influences of grid orientation on the results of reservoir simulation in oil reservoir drived by water[J]. Journal of JiangHan Petroleum Institute, 1990, 12(1): 40-45. [本文引用:1]
[3] Heinemann Z E, Brand C W. Gridding techniques in reservoir simulation[C]∥Proceedings of the First and Second International Forum on Reservoir Simulation, Alpbach, Austria, 1989: 339-426. [本文引用:2]
[4] Palagi C L, Aziz K. Use of voronoi grid in reservoir simulation[J]. SPE Advanced Technology Series, 1994, 2(2): 1-9. [本文引用:2]
[5] 向祖平, 张烈辉, 陈中华, 等. 油藏任意约束平面域PEBI网格的生成算法[J]. 西南石油学院学报 2006, 28(2): 32-36.
Xiang Zu-ping, Zhang Lie-hui, Chen Zhong-hua, et al. Algorithm for constructing PEBI mesh of arbitrarily shaped and constrained planar domains in oil reservoir[J]. Journal of Southwest Petroleum Institute, 2006, 28(2): 32-36. [本文引用:2]
[6] 蔡强, 杨钦, 孟宪海, 等. 二维PEBI网格的生成[J]. 工程图学学报, 2005, 26(2): 169-172.
Cai Qiang, Yang Qin, Meng Xian-hai, et al. Research on 2D PEBI grid generation[J]. Journal of Engineering Graphics, 2005, 26(2): 169-172. [本文引用:2]
[7] 查文舒, 李道伦, 卢德唐, 等. 井间干扰条件下PEBI网格划分研究[J]. 石油学报, 2008, 29(5): 742-746.
Zha Wen-shu, Li Dao-lun, Lu De-tang, et al. PEBI grid division in inter-well interference area[J]. Acta Petrolet Sinca, 2008, 29(5): 742-746. [本文引用:1]
[8] 王星, 常铁龙, 马艳, 等. 基于PEBI网格的多分支水平井井型优化研究[J]. 钻采工艺, 2010, 33(4): 45-48.
Wang Xing, Chang Tie-long, Ma Yan, et al. Optimization of multi-lateral horizontal wells based on PEBI grid[J]. Drilling and Production Technology, 2010, 33(4): 45-48. [本文引用:1]
[9] 刘立明, 廖新维, 陈钦雷. 混合PEBI网格精细油藏数值模拟应用研究[J]. 石油学报, 2003, 24(3): 64-67.
Liu Li-ming, Liao Xin-wei, Chen Qin-lei. Usage of hybrid PEBI grid in fine reservoir simulation[J]. Acta Petrolei Sinca, 2003, 24(3): 64-67. [本文引用:1]
[10] 王代刚, 侯健, 邢学军, 等. 基于前沿推进的改进型PEBI网格生成方法[J]. 计算物理, 2012, 29(5): 675-683.
Wang Dai-gang, Hou Jian, Xing Xue-jun, et al. Modified PEBI grid generation method with advanceing front approach[J]. Chinese Journal of Computational Physics, 2012, 29(5): 675-683. [本文引用:1]
[11] Delaunay Boris. Sur la sphere vide[J]. Bulletin of the Academy of Sciences of the USSR, Classe des Sciences Mathematiques et Naturelles, 1934(8): 793-800. [本文引用:2]
[12] Thiessen A H. Precipitation averages for large areas[J]. Monthly Weather Review, 1911, 39(7): 1082-1084. [本文引用:1]
[13] 李海峰, 吴冀川, 刘建波, 等. 有限元网格剖分与网格质量判定指标[J]. 中国机械工程, 2012, 23(3): 368-377.
Li Hai-feng, Wu Ji-chuan, Liu Jian-bo, et al. Finite element mesh generation and decision criteria of mesh quality[J]. China Mechanical Engineering, 2012, 23(3): 368-377. [本文引用:1]
[14] 丁永祥. 约束Delaunay三角剖分与有限元网格自动生成[J]. 华中理工大学学报, 1995, 23(6): 39-43.
Ding Yong-xiang. The constrained delaunay triangulation and the automatic generation of finite element meshes[J]. Journal of Huazhong University of Science and Technology, 1995, 23(6): 39-43. [本文引用:2]
[15] Okabe A, Boots B, Sugihara K, et al. Spatial Tessellations: Concepts and Applications of Voronoi Diagrams[M]. 2nd ed. Chichester: John Wiley & Sons, 2008. [本文引用:1]
[16] Brassel K E, Reif D. A procedure to generate thiessen polygons[J]. Geographical Analysis, 1979, 11(3): 289-303. [本文引用:1]
[17] 刘少华, 罗小龙, 何幼斌, 等. 基于Delauany三角网的泰森多边形生成算法研究[J]. 长江大学学报(自然科学版)理工卷, 2007, 4(1): 100-103.
Liu Shao-hua, Luo Xiao-long, He You-bin, et al. Based on Delauany theissen polygon generation algorithm of triangulation[J]. Journal of Yangtze University(Natural Science Edition)Science and Engineering Volume, 2007, 4(1): 100-103. [本文引用:1]
[18] Yang Yan-lin, Xu Tian-fu, Wang Fu-gang, et al. A user friendly pre-processing and post-processing graphical interface graphical for toughreact transport of unsaturated groundwater and heat[C]∥TOUGH Symposium, Berkely, USA, 2012: 814-822. [本文引用:1]
[19] 李孟涛, 单文文, 刘先贵, 等. 超临界二氧化碳混相驱油机理实验研究[J]. 石油学报, 2006, 27(3): 80-83.
Li Meng-tao, Shan Wen-wen, Liu Xian-gui, et al. Laboratory study on miscible oil displacement mechanism of supercritical carbon dioxide[J]. Acta Petrologica Sinica, 2006, 27(3): 80-83. [本文引用:1]