基于随机共振和MIMO技术的协方差矩阵频谱感知算法

引用本文

赵晓晖, 李晓燕. 基于随机共振和MIMO技术的协方差矩阵频谱感知算法. 2015, 45(4): 1297-1303
ZHAO Xiao-hui, LI Xiao-yan. Covariance matrix spectrum sensing algorithm based on stochastic resonance and MIMO technology. Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1297-1303 复制到剪切板

Permissions

基于随机共振和MIMO技术的协方差矩阵频谱感知算法

赵晓晖, 李晓燕

吉林大学通信工程学院,长春 130012

作者简介:赵晓晖(1957-),男,教授,博士生导师.研究方向:信号处理理论在通信中的应用.E-mail:xhzhao@jlu.edu.cn

基金:国家自然科学基金项目 (61171079)

摘要

在认知无线电系统中,为了使认知用户可以在低信噪比和衰落信道的条件下实现可靠的频谱感知,提出了基于随机共振和MIMO的协方差矩阵频谱感知算法。该算法将随机共振和MIMO技术用于协方差矩阵频谱感知,同时还给出了判决门限的计算方法。仿真实验结果表明:与不使用随机共振和MIMO技术的频谱感知算法相比,本文算法具有更高的检测性能;并且当天线数足够多时,该算法可以在很低信噪比情况下实现可靠的频谱感知。

关键词: 通信技术; 频谱感知; 随机共振; MIMO技术; 协方差矩阵

中图分类号:TN929 文献标志码:A 文章编号:1671-5497(2015)04-1297-07

Covariance matrix spectrum sensing algorithm based on stochastic resonance and MIMO technology

ZHAO Xiao-hui, LI Xiao-yan

College of Communication Engineering, Jilin University, Changchun 130012,China

Abstract

In order to achieve reliable spectrum sensing by users under the condition of low Signal-to-Noise Ratio (SNR) and fading channel in cognitive radio systems, a new covariance matrix spectrum sensing algorithm based on stochastic resonance and Multi-input-Multi-output (MIMO) technology is proposed; and the calculation method of the decision threshold is derived. Simulations show that the performance of the proposed algorithm is batter than the algorithm without introduction of the stochastic resonance and MIMO technology. When the number of antennae is large enough, the proposed method can achieve good performance at low SNR.

Keyword: communications; spectrum sensing; stochastic resonance; MIMO technology; covariance matrix

Show Figures

0 引言

随着无线通信技术的飞速发展, 频谱资源短缺问题日益凸显, 严重制约现代无线通信技术的发展和应用。为了解决这一问题, 1999年, Mitola等^{[1, 2]}提出了认知无线电的思想。认知无线电技术通过动态利用空闲的频谱资源, 可以有效地提高频谱的利用效率。而频谱感知技术在认知无线电技术中扮演着重要角色。正确的频谱感知是实现频谱动态利用的前提。

随机共振是在研究古气象冰川融化问题时提出的概念^{[3, 4, 5]}。随机共振系统是一个非线性系统。当固定输入有用信号的幅值时, 随着输入噪声信号强度的增加, 随机共振系统的输出信噪比先增加后减小, 即当噪声强度取合适值时, 随机共振系统的输出信噪比最大。随机共振系统输出信噪比最大时, 随机共振系统、输入有用信号强度和噪声信号强度达到匹配, 噪声能量会向有用信号能量转移, 从而使随机共振系统的输出信噪比增加。由于随机共振的这个优点, 随机共振理论被应用于微弱信号检测问题中, 并取得了很好的效果。鉴于随机共振可以检测微弱信号, 一些学者将随机共振理论引入到认知无线电频谱感知问题中, 以实现低信噪比条件下可靠的频谱感知^{[6, 7, 8, 9]}。

当信号使用MIMO天线进行传输时, 该信号会通过多条路径传送到接收端, 而该信号在每条路径上都受到很大衰减的可能性很小, 接收端总能获得相对满意的信号^[10]。因此, MIMO技术可以提供空间分集, 使接收端获得更多的信号副本, 有效抵抗信道衰落对通信造成的影响。因此将MIMO技术应用到频谱感知技术中, 在衰落信道条件下, 该频谱感知算法仍然能取得很好的检测性能^{[11, 12]}。

由于能量频谱感知需要知道噪声的方差, 而随机共振是很复杂的非线性系统, 噪声通过随机共振系统后, 很难计算出输出噪声的方差。为解决这一难题, 文献[7]采用最大化检测概率的方法来确定随机共振系统输出噪声的方差。但是采用这种方法得到的噪声方差与随机共振系统输出噪声方差的真实值有偏差, 这种偏差会影响到频谱感知的检测性能。基于协方差矩阵的频谱感知算法不需要任何主用户信号和噪声信号的先验信息^[13], 而且还可以克服噪声不确定性带来的影响, 因此, 本文将随机共振理论和MIMO技术应用到协方差矩阵频谱感知中, 提出基于随机共振和MIMO技术的协方差矩阵频谱感知算法。

1 系统模型

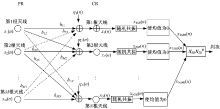
假设主用户具有M根发射天线, 认知用户具有N根接收天线, 如图1所示。

	Figure Option View Download New Window
	图1 系统模型Fig.1 System model

值得注意的是在随机共振系统中, 要求输入信号s(t)的频率足够小^[3], 而认知无线电中的信号不直接满足这一要求。但是, 可先将高频信号变换为低频信号, 然后再将此低频信号输入到随机共振系统中; 或者对随机共振系统参数进行改进, 使改造后的随机共振系统可以用于高频信号。有很多方法可以解决上述问题^{[14, 15, 16]}。例如文献[14]通过尺度变换将高频信号转换为低频信号; 文献[15]将随机共振系统的非微分项乘以某系数, 使随机共振系统能够应用于高频信号; 文献[16]则用二次采样的方法, 将高频信号转换为低频信号。本论文的研究重点是将随机共振理论和MIMO技术结合在一起来进行频谱感知, 因此不再赘述将高频信号转换为低频信号的过程, 直接令输入信号为:

$\begin{matrix} s (t) = Asin (2 πft + φ) (1) \end{matrix}$

式中f的值很小。

认知用户第i根天线第n时刻接收到的信号可以表示为:

$\begin{matrix} x_{i} (n) = \{\begin{matrix} η_{i} (n), H_{0} \\ \overset{M}{\sum_{j = 1}} h_{ji} s_{j} (n) + η_{i} (n), H_{1} \end{matrix} (2) \end{matrix}$

式中:i=1, 2, …, N; x_i(n)、s_j(n)和η _i(n)分别为x_i(nT_s)、s_j(nT_s)和η _i(nT_s)的简化表示, T_s为采样间隔; x_i(n)为认知用户第i根天线第nT_s时刻接收到的信号; s_j(n)是主用户第j根天线发射、认知用户在第nT_s时刻接收到的信号; h_ji是主用户第j根天线和认知用户第i根天线之间的信道增益; η _i(n)是认知用户第i根天线第nT_s时刻接收到的噪声信号; H₀表示没有主用户信号存在的情况; H₁表示主用户信号存在的情况。假设s_j(n)的均值为0; η _i(n)是均值为0、方差为 $\begin{matrix} σ_{η}^{2} \end{matrix}$ 的高斯白噪声; h_ji服从均值为0、方差为1的高斯分布。此外, 假设认知用户不同天线接收的噪声信号相互独立, 不同天线之间的信道相互独立, 主用户信号和噪声信号互不相关, 即:

$\begin{matrix} \{\begin{matrix} E [η_{i} (n) η_{j} (n)] = σ_{η}^{2} δ_{ij} \\ E [h_{j 1 i 1} (n) h_{j 2 i 2} (n)] = δ_{j 1 j 2} δ_{i 1 i 2} \end{matrix} (3) \end{matrix}$

式中:δ _ij= $\begin{matrix} \{\begin{matrix} 1, i = j \\ 0, i \neq j \end{matrix} \end{matrix}$

2 本文算法

2.1 算法基本原理

由图1所示, 首先将每根天线接收到的信号x_i(n), i=1, 2, …, N, 分别输入到随机共振系统中。以认知用户第i根天线为例, 所采用的离散随机共振系统如下式^{[7, 17]}:

$\begin{matrix} \begin{matrix} \frac{x_{iSR} (n + 1) - x_{iSR} (n)}{Δt} = \\ a x_{iSR} (n) - b x_{iSR}^{3} (n) + p x_{i} (n) (4) \end{matrix} \end{matrix}$

式中:随机共振系统的初值x_iSR(0)是(-1, 1)区间内的随机值; x_i(n)为随机共振系统输入信号, 它既包括主用户信号又包括噪声信号; x_iSR(n)是随机共振系统的输出信号; a、b和p是常数; Δ t为采样间隔T_s。上节提到, x_i(n)分别为x_i(nT_s)的简化表示, 因此, 随机共振系统输出信号x_iSR(n)相邻点的时间间隔为Δ t。调节p的值可以调节随机共振系统中主用户信号和噪声信号的信号强度。当p取合适的值时, 随机共振系统、主用户信号强度和噪声信号强度三者达到匹配, 随机共振系统的输出信噪比最大, 此时p的值记为p_opt。a、b和p_opt选取方法将在后文中介绍。

将p_opt带入式(4)可得:

$\begin{matrix} \begin{matrix} \frac{x_{iSR} (n + 1) - x_{iSR} (n)}{Δt} = \\ a x_{iSR} (n) - b {x_{iSR}}^{3} (n) + p_{opt} x_{i} (n) (5) \end{matrix} \end{matrix}$

在H₁的情况下, 主用户信号和噪声信号相互独立, 随机共振系统的输出信号x_iSR可以被分为两部分^[7], 分别为s_iSR(n)和η _iSR(n), 如下式:

$\begin{matrix} x_{iSR} (n) = s_{iSR} (n) + η_{iSR} (n) (6) \end{matrix}$

式中:s_iSR(n)和η _iSR(n)分别为对应 $\begin{matrix} \overset{M}{\sum_{j = 1}} \end{matrix}$ h_jis_j(n)和η _i(n)的输出。因此通过随机共振系统后, 频谱感知的二元假设检测模型为:

$\begin{matrix} x_{iSR} (n) = \{\begin{matrix} η_{iSR} (n), H_{0} \\ s_{iSR} (n) + η_{iSR} (n), H_{1} \end{matrix} (7) \end{matrix}$

根据随机共振的基本原理, 当主用户信号强度比较小时, E[x_iSR]≠ 0。由于无法控制主用户信号的输入幅度, 因此E[x_iSR]≠ 0的可能性很大。为了在任何情况下都有E[x_iSR]=0, 对x_iSR(n)做如下处理:

$\begin{matrix} \begin{matrix} x_{iSR 0} (n) = x_{iSR} (n) - E [x_{iSR}] = \\ \{\begin{matrix} η_{iSR 0} (n), H_{0} \\ s_{iSR 0} (n) + η_{iSR 0} (n), H_{1} \end{matrix} (8) \end{matrix} \end{matrix}$

式中:E[x_iSR]= $\begin{matrix} \frac{1}{N_{s}} \end{matrix} \begin{matrix} \overset{N_{s}}{\sum_{n = 1}} \end{matrix}$ x_iSR(n), 其中N_s是每根天线的采样点数。

由于随机共振系统的非线性, η _iSR₀(n)不再是高斯白噪声, 即当τ ≠ 0时R_i(τ )≠ 0。由于在确定频谱感知判决门限γ 时需要计算R_i(τ )的值, 而R_i(τ )的计算比较复杂, 这使后文计算判决门限γ 变得困难。但是, R_i(τ )随τ 的增加按负指数形式减小^[18], 当τ ≥ τ ₀时, R_i(τ )很小, 可近似为0。上节提到随机共振系统输出信号x_iSR(n)相邻点的时间间隔为Δ t, 因此令随机共振系统的步长Δ t≥ τ ₀, 这样随机共振输出噪声η _iSR₀(n)任意两个不同点之间的相关函数很小, 从而使输出噪声η _iSR₀(n)近似为白噪声。这使确定判决门限γ 变得容易。R_i(τ )的计算方法如下:

$\begin{matrix} R_{i} (τ) = \frac{1}{N_{s}} \overset{N_{s}}{\sum_{n = 1}} η_{iSR 0} (n) η_{iSR 0} (n - \frac{τ}{Δt}) (9) \end{matrix}$

式中:τ =0, Δ t, 2Δ t, …。

采用文献[13]中介绍的协方差矩阵频谱感知算法进行频谱感知, 构造如下矩阵:

X_SR= $\begin{matrix} [\begin{matrix} x_{1 SR 0} (1) & x_{1 SR 0} (2) & \dots & x_{1 SR 0} (N_{s}) \\ x_{2 SR 0} (1) & x_{2 SR 0} (2) & \dots & x_{2 SR 0} (N_{s}) \\ ⋮ & ⋮ & ⋮ \\ x_{NSR 0} (1) & x_{NSR 0} (2) & \dots & x_{NSR 0} (N_{s}) \end{matrix}] \end{matrix}$

s_SR= $\begin{matrix} [\begin{matrix} s_{1 SR 0} (1) & s_{1 SR 0} (2) & \dots & s_{1 SR 0} (N_{s}) \\ s_{2 SR 0} (1) & s_{2 SR 0} (2) & \dots & s_{2 SR 0} (N_{s}) \\ ⋮ & ⋮ & ⋮ \\ s_{NSR 0} (1) & s_{NSR 0} (2) & \dots & s_{N SR 0} (N_{s}) \end{matrix}] \end{matrix}$

η _SR= $\begin{matrix} [\begin{matrix} η_{1 SR 0} (1) & η_{1 SR 0} (2) & \dots & η_{1 SR 0} (N_{s}) \\ η_{2 SR 0} (1) & η_{2 SR 0} (2) & \dots & η_{2 SR 0} (N_{s}) \\ ⋮ & ⋮ & ⋮ \\ η_{NSR 0} (1) & η_{NSR 0} (2) & \dots & η_{NSR 0} (N_{s}) \end{matrix}] \end{matrix}$

则接收信号的协方差矩阵表示为:

$\begin{matrix} \begin{matrix} R (N_{s}) = \frac{1}{N_{s}} X_{SR} {X^{T}}_{SR} = \\ \{\begin{matrix} η_{SR} {η^{T}}_{SR} \\ s_{SR} {s^{T}}_{SR} + η_{SR} {η^{T}}_{SR} \end{matrix} \approx \\ \{\begin{matrix} σ^{2} I \\ σ^{2} I + R_{SSR} \end{matrix} (10) \end{matrix} \end{matrix}$

式中:σ ²为随机共振系统输出噪声η _iSR₀(n)的方差, i=1, 2, …, N。

由于每根天线接收到噪声的方差均为 $\begin{matrix} σ_{η}^{2} \end{matrix}$ , 每根天线将信号x_i(n)输入到参数相同的随机共振系统, 且随机共振系统输出噪声的自相关函数只取决于输入噪声强度和随机共振系统参数, 因此随机共振系统输出噪声的方差只决定于输入噪声强度和随机共振系统参数^[18]。因此, 所有随机共振系统的输出噪声方差相等。

由式(10)可以看出, 在H₀情况下, 协方差矩阵趋向于对角矩阵; 而在H₁情况下则不会趋向于对角矩阵。可以根据上述不同来判断主用户信号是否存在。根据中心极限定理, 当N_s很大时η _SR $\begin{matrix} {η^{T}}_{SR} \end{matrix}$ 中元素可近似服从高斯分布。

定义如下变量:

$\begin{matrix} \begin{matrix} T_{1} (N_{s}) = \frac{1}{N} \overset{N}{\sum_{n = 1}} \overset{N}{\sum_{m = 1}} | r_{n, m} (N_{s}) | (11) \\ T_{2} (N_{s}) = \frac{1}{N} \overset{N}{\sum_{n = 1}} | r_{n, n} (N_{s}) | (12) \end{matrix} \end{matrix}$

式中:r_n_,_m $\begin{matrix} (N_{s}) \end{matrix}$ 是R $\begin{matrix} (N_{s}) \end{matrix}$ 矩阵第n行、第m列的元素。

协方差矩阵频谱感知算法的检测统计量为:

$\begin{matrix} T_{x} = T_{1} (N_{s}) / T_{2} (N_{s}) (13) \end{matrix}$

判决表达式为:

由于不知道主用户信号的先验信息, 故不能根据检测概率P_d确定判决门限γ 。通常情况下, 利用虚警概率来确定γ 。设定虚警概率为固定的值P_fa, 确定γ 使频谱感知算法的虚警概率等于P_fa。本文确定判决门限的方法与文献[13]中确定判决门限的方法类似。

根据式(10), 在H₀条件下有

$\begin{matrix} \begin{matrix} r_{n, m} (N_{s}) = \frac{1}{N_{s}} \overset{N_{s}}{\sum_{i = 1}} η_{nSR 0} (i) η_{mSR 0} (i) (15) \\ \begin{matrix} r_{n, m} {(N_{s})}^{2} = \\ \frac{1}{N_{s}^{2}} \overset{N_{s}}{\sum_{i_{1} = 1}} \overset{N_{s}}{\sum_{i_{2} = 1}} η_{nSR 0} (i_{1}) η_{mSR 0} (i_{1}) η_{nSR 0} (i_{2}) η_{mSR 0} (i_{2}) \end{matrix} (16) \end{matrix} \end{matrix}$

式中:η _iSR₀(n)是矩阵η _SR中的元素。

当n=m时, 有

$\begin{matrix} \{\begin{matrix} E [r_{n, m} (N_{s})] = σ^{2} \\ var (r_{n, m} (N_{s})) = 2 σ^{2} / N_{s} \end{matrix} (17) \end{matrix}$

当n≠ m时, 有:

$\begin{matrix} \{\begin{matrix} E [r_{n, m} (N_{s})] = 0 \\ var (r_{n, m} (N_{s})) = σ^{2} / N_{s} \end{matrix} (18) \end{matrix}$

由中心极限定理可知, 在H₀条件下, r_n_,_m(N_s)服从高斯分布。经计算可得:

$\begin{matrix} E [| r_{n, m} (N_{s}) |] = σ^{2} \sqrt[]{\frac{2}{π N_{s}}} (19) \end{matrix}$

根据式(17)和(19)可得

$\begin{matrix} \begin{matrix} E [T_{1} (N_{s})] = (1 + (N - 1) \sqrt[]{\frac{π}{2 N_{s}}}) σ^{2} \\ E [T_{2} (N_{s})] = σ^{2} \\ var (T_{2} (N_{s})) = \frac{2 σ^{2}}{N_{s}} \end{matrix} \end{matrix}$

根据中心极限定理, 在H₀条件下, 当N_s比较大时, T₂服从正态分布。因此虚警概率为:

$\begin{matrix} \begin{matrix} P_{fa} = P {T_{x} > γ} \approx P {T_{2} (N_{s}) < \frac{1}{γ} E [T_{1} (N_{s})]} = \\ Q (\frac{\frac{1}{γ} (1 + (N - 1) \sqrt[]{\frac{2}{N_{s} π}}) - 1}{\sqrt[]{\frac{2}{N_{s}}}}) (20) \end{matrix} \end{matrix}$

式中:Q(t)= $\begin{matrix} \frac{1}{2 π} \end{matrix} \begin{matrix} \int_{-}^{\infty} \end{matrix} \begin{matrix} e^{- x^{2} / 2} \end{matrix}$ dx。

判决门限的计算公式为:

$\begin{matrix} γ = \frac{1 + (N - 1) \sqrt[]{\frac{2}{N_{s} π}}}{1 + Q^{- 1} (P_{fa}) \sqrt[]{\frac{2}{N_{s}}}} (21) \end{matrix}$

2.2 随机共振参数的确定

本文采用式(5)所示的随机共振系统, 下面给出p_opt的确定方法。

若主用户信号如式(1)所示, 则输入信号信噪比为:

$\begin{matrix} SN R_{in} = \frac{A^{2}}{2 σ_{η}^{2}} (22) \end{matrix}$

当信号通过如式(4)所示的随机共振系统后, 随机共振系统的输出信噪比为^{[3, 7]}:

$\begin{matrix} SN R_{out} = \frac{\sqrt[]{2} a p^{2} A^{2} x_{m}^{2}}{(p^{2} σ_{η}^{2})^{2}} e^{\frac{- 2 U_{0}}{p^{2} σ_{η}^{2}}} (23) \end{matrix}$

式中:x_m= $\begin{matrix} \sqrt[]{\frac{a}{b}} \end{matrix}$ ; U₀= $\begin{matrix} \frac{a^{2}}{4 b} \end{matrix}$ 。

为了求出使信噪比最大的p_opt, 令 $\begin{matrix} \frac{\partial SN R_{out}}{\partial p} \end{matrix}$ =0, 则有:

$\begin{matrix} p_{opt} = \sqrt[]{U_{0} / σ_{η}^{2}} (24) \end{matrix}$

为了提高随机共振系统的输出增益, 则必须有下式成立:

$\begin{matrix} SN R_{gain} = \frac{SN R_{out}}{SN R_{in}} = 2 \sqrt[]{2} a x_{m}^{2} e^{- 2} > 1 (25) \end{matrix}$

由式(24)和(25)可得:

$\begin{matrix} \frac{a^{2}}{b} > \frac{e^{2}}{2 \sqrt[]{2}} (26) \end{matrix}$

因此, 在选取随机共振系统参数时, 要满足上式要求。本文选取a=10, b=1。

3 仿真实验结果与分析

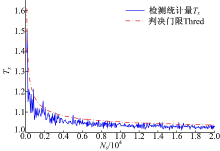
本节通过仿真验证基于随机共振和MIMO的协方差矩阵频谱感知算法(即SR-MIMO协方差矩阵频谱感知算法)的有效性, 从多个方面对单天线协方差矩阵的频谱感知算法、MIMO协方差矩阵频谱感知算法和SR-MIMO协方差矩阵频谱感知算法进行比较。仿真采用蒙特卡罗的方法得到检测概率P_d, 主用户信号为BPSK信号, 信号的频率为f=0.1; 噪声的方差为 $\begin{matrix} σ_{η}^{2} \end{matrix}$ =1; 为了方便起见, 仿真中令M=N。

图2给出在H₀条件下, 检测统计量T_x=T₁(N_s)/T₂(N_s)与判决门限γ 的关系, 其中M=N=5。从图2可以看出, 随着N_s的变化, 判决门限γ 进行动态调整, 这可以保证判决门限选择的合理性。此外, 在主用户信号不存在的条件下, T_x曲线在γ 曲线的下方, 这充分说明判决门限的计算方法是正确的。

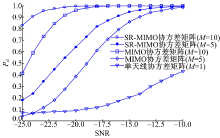
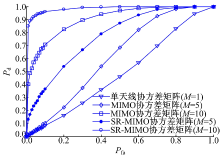
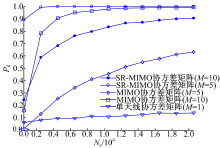
	Figure Option View Download New Window
	图2 判决门限的有效性Fig.2 Validity of decision threshold

图3、图4和图5分别给出SR-MIMO协方差矩阵频谱感知算法的检测概率、MIMO协方差矩阵频谱感知算法的检测概率和单天线协方差矩阵频谱感知算法的检测概率随信噪比、虚警概率和采样点变化的仿真曲线。在图3和图4中取N_s=1000; 在图4中, 单天线协方差矩阵频谱感知算法和MIMO协方差矩阵频谱感知算法在SNR=-22 dB条件下进行仿真; SR-MIMO协方差矩阵频谱感知算法在SNR=-25 dB的条件下进行仿真。从图3可以看出, 在信噪比为-10 dB时, 单天线协方差频谱感知算法的检测概率为0.41。而MIMO协方差矩阵频谱感知算法的检测概率为0.995, SR-MIMO协方差矩阵频谱感知算法的检测概率达到1; 当M=N=10时, 在SNR=-20 dB条件下, SR-MIMO协方差矩阵频谱感知算法的检测概率能达到1。图4是频谱感知的ROC曲线。图5中所有曲线都随采样点的增加而增加。

	Figure Option View Download New Window
	图3 两种算法在不同信噪比下的性能比较Fig.3 Performance comparison of two algorithms under different SNR

	Figure Option View Download New Window
	图4 两种频谱感知算法的ROC曲线Fig.4 ROC curves of spectrum sensing algorithms

	Figure Option View Download New Window
	图5 不同算法在不同采样点数下的性能比较Fig.5 Performance of different algorithms at different sampling points

由图3、图4和图5可见, 基于MIMO的协方差矩阵频谱感知算法和SR-MIMO协方差矩阵频谱感知算法的仿真曲线均在单天线协方差矩阵频谱感知算法仿真曲线的上方; 并且在两种算法使用天线数目相同的情况下, SR-MIMO协方差矩阵频谱感知算法的仿真曲线在MIMO协方差矩阵频谱感知算法仿真曲线的上方。因此图3、图4和图5的仿真结果均表明基于MIMO的频谱感知算法的检测概率要远高于单天线频谱感知算法的检测概率; 而基于MIMO和随机共振的协方差矩阵频谱感知算法的检测概率最高。即本文算法的性能要优于其他两种算法。

4 结束语

提出了基于随机共振和MIMO的协方差矩阵频谱感知算法。通过随机共振增加输入信号的信噪比, 利用MIMO技术获得空间分集以抵抗信道衰落对频谱感知造成的影响。该频谱感知算法可以在低信噪比和衰落信道条件下取得很高的检测性能。仿真结果表明, 该频谱感知算法的性能要优于单天线协方差矩阵频谱感知算法和基于MIMO的协方差矩阵频谱感知算法。同时仿真实验也验证了该算法的有效性, 而且在低信噪比条件下, 该算法仍能进行可靠的频谱感知。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Mitola J, Magutre G Q. Cognitive radio: making software radios more personal[J]. IEEE Personal Communications, 1999, 6(4): 13-17. [本文引用:1]
[2]	Mitola J. Cognitive radio: an intergrated agent architecture for software defined radio[D]. Kista Sweden: Royal Institute of Technology, 2000. [本文引用:1]
[3]	McNamara B, Wilesenfeld K. Theory of stochastic resonance[J]. Phys Rev A, 1989, 39(9): 4854-4869. [本文引用:3]
[4]	Benzi R, Sutera A, Vulpiani A. The mechanism of stochastic resonance[J]. J Phys A: Math Gen, 1981, 14(11): 453-457. [本文引用:1]
[5]	Gammaitoni L, Hanggi P, Jung P, et al. Stochastic resonace[J]. Reviews of Modern Physics, 1998, 70(1): 223-287. [本文引用:1]
[6]	He D, Li W H, Zhu F S, et al. An enhanced covariance spectrum sensing technique based on stochastic resonance in cognitive radio networks[C]∥IEEE International Symposium on Circuits and Systems (ISCAS), Seoul, 2012: 818-821. [本文引用:1]
[7]	He D, Lin Y P, He C, et al. A novel spectrum-sensing techique in cognitive radio based on stochastic resonance[J]. IEEE Transactions on Vehicular Technology, 2010, 59(4): 1680-1688. [本文引用:4]
[8]	Chen W, Wang J, Li H S, et al. Stochastic resonance noise enhanced spectrum sensing in cognitive radio networks[C]∥IEEE Global Telecommunications Conference (GLOBECOM), Miami, 2010. [本文引用:1]
[9]	Zheng K, Li H S, Djouadi S M, et al. Spectrum sensing in low snr regime via stochastic resonance[C]∥The 44th Annual Conference on Information Sciences and Systems (CISS), Princeton, 2010. [本文引用:1]
[10]	Mietzner J, Schober R, Lampe L, et al. Multiple-antenna techniques for wireless communications—a comprehensive literature survey[J]. IEEE Communications Surveys and Tutorials, 2009, 11(2): 87-105. [本文引用:1]
[11]	Zeng Y H, Liang Y C. Eigenvalue-based spectrum sensing algorithms for cognitive radio[J]. IEEE Transactions on Communications, 2009, 57(6): 1784-1793. [本文引用:1]
[12]	Soltanmohammadi E M, Orooji M, Naraghi-Pour M. Spectrum sensing over MIMO channels using generalized likelihood ratio tests[J]. IEEE Signal Processing Letters, 2013, 20(5): 439-442. [本文引用:1]
[13]	Zeng Y H, Liang Y C. Spectrum-sensing algorithms for cognitive radio based on statistical covariances[J]. IEEE Transactions on Vehicular Technology, 2009, 58(4): 1804-1815. [本文引用:1]
[14]	Wang G F, Zhang H R, Zhang F Q, et al. Scale transformation for detecting weak periodic signal of stochastic resonance[C]∥International Conference on Intelligent Computing and Integrated Systems (ICISS), Guilin, China, 2010. [本文引用:1]
[15]	Wang J H, Xiao Q, Li X. The high-frequency weak signal detection based on stochastic resonance[C]∥International Conference on Test and Measurement, Hong Kong, 2009. [本文引用:1]
[16]	冷永刚, 王太勇. 二次采样用于随机共振从强噪声中提取弱信号的数值研究[J]. 物理学报, 2003, 52(10): 2432-2437. Leng Yong-gang, Wang Tai-yong. Numerical research of twice sampling stochastic resonance for the detection of a weak signal submerged in a heavy noise[J]. Acta Physica Sinica, 2003, 52(10): 2432-2437. [本文引用:1]
[17]	Anishchenko V S, Astakhov V, Neiman A, et al. Nonlinear Dynamics of Chaotic and Stochastic Systems[M]. Berlin: Springer-Verlag, 2002. [本文引用:1]
[18]	冷永刚, 王太勇, 郭焱. 级联双稳定系统的随机共振特性[J]. 物理学报, 2005, 54(3): 1118-1125. Leng Yong-gang, Wang Tai-yong, Guo Yan. Stochastic resonance behaviors of bistable systems connected in series[J]. Acta Physica Sinica, 2005, 54(3): 1118-1125. [本文引用:2]

1999

0.0

... 为了解决这一问题,1999年,Mitola等^[1,2]提出了认知无线电的思想 ...

2000

0.0

... 为了解决这一问题,1999年,Mitola等^[1,2]提出了认知无线电的思想 ...

1989

0.0

... 随机共振是在研究古气象冰川融化问题时提出的概念^[3,4,5] ...

... 值得注意的是在随机共振系统中,要求输入信号s(t)的频率足够小^[3],而认知无线电中的信号不直接满足这一要求 ...

... 当信号通过如式(4)所示的随机共振系统后,随机共振系统的输出信噪比为^[3,7]: ...

1981

0.0

... 随机共振是在研究古气象冰川融化问题时提出的概念^[3,4,5] ...

1998

0.0

... 随机共振是在研究古气象冰川融化问题时提出的概念^[3,4,5] ...

2012

0.0

... 鉴于随机共振可以检测微弱信号,一些学者将随机共振理论引入到认知无线电频谱感知问题中,以实现低信噪比条件下可靠的频谱感知^[6,7,8,9] ...

2010

0.0

... 鉴于随机共振可以检测微弱信号,一些学者将随机共振理论引入到认知无线电频谱感知问题中,以实现低信噪比条件下可靠的频谱感知^[6,7,8,9] ...

... 以认知用户第i根天线为例,所采用的离散随机共振系统如下式^[7,17]: ...

... 在H₁的情况下,主用户信号和噪声信号相互独立,随机共振系统的输出信号x_iSR可以被分为两部分^[7],分别为s_iSR(n)和#cod#x003b7 ...

... 当信号通过如式(4)所示的随机共振系统后,随机共振系统的输出信噪比为^[3,7]: ...

2010

0.0

... 鉴于随机共振可以检测微弱信号,一些学者将随机共振理论引入到认知无线电频谱感知问题中,以实现低信噪比条件下可靠的频谱感知^[6,7,8,9] ...

2010

0.0

... 鉴于随机共振可以检测微弱信号,一些学者将随机共振理论引入到认知无线电频谱感知问题中,以实现低信噪比条件下可靠的频谱感知^[6,7,8,9] ...

2009

0.0

... 当信号使用MIMO天线进行传输时,该信号会通过多条路径传送到接收端,而该信号在每条路径上都受到很大衰减的可能性很小,接收端总能获得相对满意的信号^[10] ...

2009

0.0

... 因此将MIMO技术应用到频谱感知技术中,在衰落信道条件下,该频谱感知算法仍然能取得很好的检测性能^[11,12] ...

2013

0.0

... 因此将MIMO技术应用到频谱感知技术中,在衰落信道条件下,该频谱感知算法仍然能取得很好的检测性能^[11,12] ...

2009

0.0

... 基于协方差矩阵的频谱感知算法不需要任何主用户信号和噪声信号的先验信息^[13],而且还可以克服噪声不确定性带来的影响,因此,本文将随机共振理论和MIMO技术应用到协方差矩阵频谱感知中,提出基于随机共振和MIMO技术的协方差矩阵频谱感知算法 ...

2010

0.0

... 有很多方法可以解决上述问题^[14,15,16] ...

2009

0.0

... 有很多方法可以解决上述问题^[14,15,16] ...

2003

0.0

. 2003, 52(10):2432-2437 DOI:doi:10.3321/j.issn:1000-3290.2003.10.014

Numerical research of twice sampling stochastic resonance for the detection of a weak signal submerged in a heavy noise

二次采样用于随机共振从强噪声中提取弱信号的数值研究

Leng Yong-gang , Wang Tai-yong.

冷永刚, 王太勇

A new technique, twice sampling stochastic resonance (SR), is proposed, and with this technique, the goal of detecting a weak signal overwhelmed in a noise is r ealized under large parameters in terms of the theory of adiabatic elimination. For the purpose of practical applications, the relative parameters are investiga ted in the detection of a weak signal based on the technique. The numerical simu lation shows that the method presented here is of potential value in the signal analysis and is expected to be applied to the practically measured data processi ng in the future.

提出了二次采样的随机共振(SR)技术，并利用该技术，实现了绝热近似理论在大参数条件下，从强噪声中提取弱信号的目标.为便于应用，研究了二次采样随机共振方法在弱信号检测中相关参数之间的关联性.数值分析表明，该法在信号分析方面有着潜在的应用价值，有望将来应用于实测信号的数据处理.

... 有很多方法可以解决上述问题^[14,15,16] ...

2002

0.0

... 以认知用户第i根天线为例,所采用的离散随机共振系统如下式^[7,17]: ...

2005

0.0

. 2005, 54(3):1118-1125 DOI:doi:10.3321/j.issn:1000-3290.2005.03.021

Stochastic resonance behaviors of bistable systems connected in series

级联双稳定系统的随机共振特性

Leng Yong-gang , Wang Tai-yong , Guo Yan.

冷永刚, 王太勇, 郭焱

The stochastic resonance(SR) characteristics of two bistable systems connected in series have been investigated. It is deduced that the first bistable system of the cascaded system is most important because of its converting a white noise into a color one, and the subsequent bistable systems continuously concentrate noise energy into lowfrequency area in terms of Lorentzian distribution, which weakens the highfrequency dithering of the last output waveform and outlines the basic shape of the wave. The law of the signal spectral amplitude varying with noise intensity indicates that within a limited lowfrequency band, the cascaded system is able to promote the height of the signal spectral spike by a certain amount of noise. If the former of the cascaded system does not stay in SR, the latter could not optimize the former output to become a SR state. With the increase of the number of the bistable systems in the cascaded system, the lowfrequency area where most of the noise energy is collected will be narrowed gradually, and hence the signal peak is easily reduced and submerged in noise. For this case, in spite of using the twice-sampling technique to improve the signal spectral spike, the improvement is limited. Therefore, a single bistable system is effective for signal detection.

研究了两个双稳系统级联的随机共振特性，由于第一级双稳系统的作用是将白噪声转变为色噪声，因此它是整个级联系统中最重要的环节，以后各级系统近似按洛伦兹分布将噪声能量不断向低频区域集中，从而减弱高频抖动，突出波形的基本轮廓.频谱中信号谱峰随噪声强度的变化规律表明，级联双稳系统只在有限的低频范围内，通过一定量的噪声强度来增强信号频率处的谱峰高度，如果前一级系统未达到随机共振状态，那么其后一级并不能对前一级的输出进行“优化”而形成随机共振.级联双稳系统级数的增加，会使噪声能量集中的低频区域变窄，信号谱峰易被压缩和受到噪声干扰.虽然可以用二次采样方法进行改善，但其改善程度有限.因此对于信号检测而言，使用单级双稳系统即可.

... 的增加按负指数形式减小^[18],当#cod#x003c4 ...

... 由于每根天线接收到噪声的方差均为 ση2,每根天线将信号x_i(n)输入到参数相同的随机共振系统,且随机共振系统输出噪声的自相关函数只取决于输入噪声强度和随机共振系统参数,因此随机共振系统输出噪声的方差只决定于输入噪声强度和随机共振系统参数^[18] ...