基于Markov链的车载自组网MAC层建模及分析

引用本文

孙伟, 张和生, 潘成, 杨军, 白喆. 基于Markov链的车载自组网MAC层建模及分析. 2015, 45(4): 1304-1310
SUN Wei, ZHANG He-sheng, PAN Cheng, YANG Jun, BAI Zhe. Modeling and analysis of the MAC layer of VANETs based on Markov chain. Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1304-1310 复制到剪切板

Permissions

基于Markov链的车载自组网MAC层建模及分析

孙伟¹, 张和生^1,², 潘成¹, 杨军¹, 白喆¹

1.北京交通大学电气工程学院,北京 100044

2.北京交通大学轨道交通控制与安全国家重点实验室,北京 100044

张和生(1970-),男,教授,博士生导师.研究方向:传感器网络,网络通信性能,智能控制.E-mail:hszhang@bjtu.edu.cn

作者简介:孙伟(1987-),男,博士研究生.研究方向:车路通信网络性能分析.E-mail:10117350@bjtu.edu.cn

基金:国家自然科学基金项目(61174179)

摘要

车载自组网底层协议IEEE 802.11p的MAC层采用增强型分布信道访问机制(EDCA),为验证该机制能否满足不同类型消息的服务质量,采用二维Markov链建立了该机制的饱和分析模型,模型考虑了不同队列类型、内部碰撞和退避挂起机制。在此基础上,分析了不同队列的归一化吞吐量、丢包率和时延性能指标,同时还研究了退避挂起机制对丢包率的影响。结果表明:随着车辆数的增加,归一化吞吐量逐渐减小,而丢包率和时延逐渐增加;高优先级队列始终有较大归一化吞吐量值、较低丢包率和较小的传输时延。验证了IEEE802.11p能够保证不同类型消息的服务质量,并为车载自组网的部署提供理论依据。

关键词: 通信技术; 车载自组网; 增强型分布信道访问; Markov链; 饱和分析模型

中图分类号:TN915 文献标志码:A 文章编号:1671-5497(2015)04-1304-07

Modeling and analysis of the MAC layer of VANETs based on Markov chain

SUN Wei¹, ZHANG He-sheng^1,², PAN Cheng¹, YANG Jun¹, BAI Zhe¹

1.School of Electrical Engineering, Beijing Jiaotong University, Beijing 100044, China

2.State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University,Beijing 100044, China

Abstract

The Enhanced Distributed Channel Assess (EDCA) mechanism is adopted by IEEE 802.11p Medium Access Control (MAC) layer, which is used in Vehicular Ad hoc Networks (VANETs). The performance of MAC layer is studied to satisfy Quality of Service (QoS) requirements of messages with different applications. The two-dimensional Markov chain is proposed to study the backoff process of the EDCA mechanism, in which different types of messages, internal collision and the frozen mechanism are taken into account. On this basis, the normalized throughput, the drop rate and time delay of messages are studied. The results show that the value of normalized throughput decreases with the increasing number of vehicles; while the drop rate and time delay are opposite. However, the higher priority category has the larger value of normalized throughput and the lower value of drop rate and time delay, which verifies that the IEEE 802.11p can provide QoS for different messages. The analysis results can also provide theoretical basis for the deployment of VANETs.

Keyword: communication; VANETs; EDCA; Markov chain; saturated analyzing model

Show Figures

0 引言

车载自组网(Vehicular ad-hoc networks, VANETs)依靠先进的信息技术和通信技术为日益严重的交通问题, 如道路拥堵和事故频发, 提供了解决方案^[1]。

在车辆间和车辆与基础设施间的通信中, VANETs采用2010年批准的IEEE 802.11p^[2]作为底层协议以解决车辆环境下的无线接入问题, 如车辆高速移动导致的通信拓扑频繁变换及不同应用类型通信性能的不同需求等。而MAC(Media access control)层在上述通信问题解决中起着重要作用。

IEEE 802.11p MAC采用IEEE 802.11e^[3]的增强型分布信道访问(Enhanced distributed channel access, EDCA)机制以提供多种应用类型的服务, 然而不同类型的服务质量(Quality of service, QoS)要求不同, 如安全类应用实时性要求较高^[4]。IEEE 802.11p MAC层对其参数进行了修改以适用于车路环境。为满足不同类型应用的QoS, 需要对IEEE 802.11p的网络性能进行分析, 并对性能指标进行求解, 如吞吐量、时延、丢包率等。

很多文献采用分析模型对IEEE 802.11e EDCA机制进行了研究。其中大部分是对Bianchi模型^[5]的改进, 如文献[6]对DCF(Distributed coordination function)的非饱和吞吐量进行了计算。文献[7]提出了基于Markov链的分析模型, 但未考虑消息内部碰撞。文献[8]建立了IEEE 802.11e的综合分析模型对其性能进行分析。文献[9, 10]使用三维Markov链对IEEE 802.11e EDCA机制的不同接入类(Access categories, ACs)性能进行了分析。文献[11]采用Markov链模型研究了IEEE 802.11p协议在安全方面的应用。文献[12]采用二维Markov链对IEEE 802.11p EDCA机制进行了分析, 该模型分析时并未考虑信道忙时退避计数器的挂起机制。

本文采用二维Markov链建立了IEEE 802.11p EDCA机制的饱和模型, 通过该模型对吞吐量、丢包率和时延进行了求解。同时还研究了退避挂起机制对丢包率的影响。结果表明, 随着通信范围内车辆数的增加, 归一化吞吐量逐渐减小, 丢包率和时延逐渐增加。高优先级队列始终有较大归一化吞吐量和较小传输时延。同样验证了IEEE 802.11p采用的EDCA机制能够保证不同应用类型的服务质量。

1 IEEE 802.11p MAC的特点

MAC层采用的EDCA机制是由DCF扩展而来, 因此其信道访问方式与DCF一致, 均为CSMA/CA(Carrier sense multiple access with collision avoidance)。EDCA定义了四类AC以保证不同优先级消息的QoS, 用AC[i](i=0, 1, 2, 3)表示。

EDCA机制中, 不同优先级的AC在其信道访问时采用不同的仲裁帧间间隔(Arbitration inter frame spacing, AIFS)和竞争窗口(Contention window, CW)值, 如表1所示。

表1 IEEE 802.11p EDCA参数值^[2] Table 1 EDCA parameters of IEEE 802.11p^[2]

AC[i](i=0, 1, 2, 3)的T_AIFS[AC[_i_]]计算公式如下^[2]:

$\begin{matrix} T_{AIFS [AC [i]]} = T_{SIFS} + N_{AIFSN [AC [i]]} T_{aSlotTime} (1) \end{matrix}$

式中:T_SIFS是短帧间间隔的持续时间(Short inter frame spacing, SIFS); T_aSlotTime是一个时隙所持续的时间; N_AIFSN[AC[_i_]]是AIFSN[AC[i]]的值。

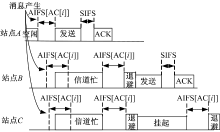
信道访问过程为:当AC[i]队列有消息发送时, 首先监听信道, 如果信道空闲持续时间超过AIFS[AC[i]], 且AC[i]的退避计数器的值为0, 则该消息直接被发送, 如图1站点A所示。如果不为0, AC[i]的退避计数器在每个空闲时隙减1, 若此时检测到信道忙, 退避计数器被挂起, 停止递减, 如图1站点C所示。此后, 站点重新监听信道, 如果信道持续空闲时间为AIFS[AC[i]], 退避计数器解挂开始递减。若退避计数器值递减为0, 站点向信道发送该消息。当同一站点内多个AC队列的退避计数器同时递减为0, 消息的同时发送导致内部碰撞。此时, 内部碰撞由站点内的虚拟调度器采用冲突避免方式选择高优先级AC消息的发送, 从而造成低优先级AC消息的重传。不同站点间消息产生碰撞时, 不论优先级高低, 消息都需重传。由表1和式(1)知, 高优先级AC具有较小的AIFS和CW值, 因此可优先获得信道访问权。

	Figure Option View Download New Window
	图1 IEEE 802.11p EDCA信道访问Fig.1 EDCA basic access mechanism of IEEE 802.11p

2 模型的建立与分析

2.1 EDCA机制的Markov链模型

MAC层在保证不同AC的QoS上起着重要作用。为了分析不同AC的QoS, 需对IEEE 802.11p MAC层所采用的EDCA机制进行建模分析。

采用EDCA机制进行信道访问时, AC的退避过程实际为退避计数器状态转移的过程, 状态间的转移符合Markov性, 即下一状态只与当前状态有关而与过去状态无关。因此可采用二维Markov链描述单个AC的退避机理, 如图2所示, 该模型分析时考虑了不同AC的不同竞争窗口值、消息的内部碰撞以及信道忙时的退避挂起机制。模型分析采用文献[10]的类似方法。在分析时, 假定信道为理想状态, 即数据包不存在由于误码导致的重传。同时假定AC队列饱和, 即每个队列始终有消息发送。

图2

Markov链中二元组{s(t), b(t)}表示信道访问的退避过程, s(t)为t时刻消息的重传次数或称退避阶段(Backoff stage)的值, b(t)为t时刻退避计数器的值。状态D_i_,_j表示退避计数器挂起时所处的状态, 即此时的退避阶段和退避计数器的值。p_b表示检测到信道忙时退避计数器的挂起概率。当退避计数器值减为0时, 站点将向信道发送该消息, 若此时同一站点内高优先级队列或其他站点同时发送消息, 则消息间发生碰撞, 其概率为p_c。碰撞使竞争窗口值加倍, 重传次数加1, 进入下次退避过程, 当超过最大重传次数m时, 消息将被丢弃。

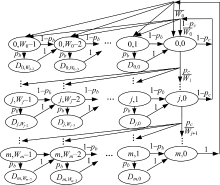	Figure Option View Download New Window
	图2 IEEE 802.11p单个AC的Markov链模型Fig.2 Signal AC Markov model of IEEE 802.11p

由图2 Markov链模型知, 消息在第j次退避阶段, 退避计数器的取值为[0, W_j-1]中的随机整数。W_j的计算式如下:

$\begin{matrix} W_{j} = \min {2^{j} (W_{\min} + 1) - 1, W_{\max}} + 1 (2) \end{matrix}$

式中:W_max=2^m'W₀-1, m'=log₂ $\begin{matrix} \frac{W_{\max} + 1}{W_{\min} + 1} \end{matrix}$ 为CW的最大增加次数; W_max和W_min分别为CW的最大值和最小值; m为消息的最大重传次数。

Markov链的一步转移概率如下:

(1)第j退避阶段, 退避计数器值从(j, k+1)状态转移到(j, k)状态, 即时隙内检测到信道空闲的概率为1-p_b, 其转移表达式为:

$\begin{matrix} \begin{matrix} P ((j, k) | (j, k + 1)) = 1 - p_{b} (3) \\ k \in [0, W_{j} - 2], j \in [0, m] \end{matrix} \end{matrix}$

(2)第j退避阶段, 退避计数器从(j, k+1)状态转移到D_i_,_k状态, 即时隙内检测到信道忙导致退避计数器挂起的概率为p_b, 其转移表达式为:

$\begin{matrix} \begin{matrix} P (D_{j, k} |(j, k + 1)) = p_{b} (4) \\ k \in [0, W_{j} - 2], j \in [0, m] \end{matrix} \end{matrix}$

(3)第j-1退避阶段, 消息发送时, 如果发生碰撞, 使得消息重传, 则重传次数加1, 并转至第j退避阶段, 其转移表达式为:

$\begin{matrix} \begin{matrix} P ((j, k) | (j - 1, 0)) = p_{c} / W_{j} (5) \\ k \in [0, W_{j} - 1], j \in [1, m] \end{matrix} \end{matrix}$

(4)第j退避阶段, 若消息成功发送, 则返回到初始阶段, 发送下一条消息, 其表达式为:

$\begin{matrix} \begin{matrix} P ((0, k) | (j, 0)) = (1 - p_{c}) / W_{0} (6) \\ k \in [0, W_{i} - 1], j \in [0, m - 1] \end{matrix} \end{matrix}$

(5)当达到最大退避阶段m时, 若消息发送成功, 则返回初始阶段发送下一消息; 反之, 则丢弃该消息, 同样返回初始阶段发送下一消息。因此在最大退避阶段以概率1返回到初始阶段。表达式为:

$\begin{matrix} \begin{matrix} P ((0, k) | (m, 0)) = 1 / W_{0} (7) \\ k \in [0, W_{i} - 1] \end{matrix} \end{matrix}$

2.2 系统稳态概率分析

Markov链中b_j_,_k= $\begin{matrix} \lim_{t \to \infty} \end{matrix}$ P(s(t)=j, b(t)=k)为系统的平稳分布, 其中j∈ [0, m], k∈ [0, W_i-1], 根据状态转移概率可得出初始退避阶段任意状态与初始状态间的关系如式(8)所示:

$\begin{matrix} \begin{matrix} b_{0, k} = \frac{W_{0} - k}{W_{0}} \frac{1}{1 - p_{b}} b_{0, 0} (8) \\ k \in [1, W_{0} - 1] \end{matrix} \end{matrix}$

相邻两个退避阶段的关系式为:

$\begin{matrix} b_{j, 0} = p_{c} b_{j - 1, 0}, j \in [1, m] (9) \end{matrix}$

通过式(8)和式(9)可得出任意状态与初始状态的关系式为:

$\begin{matrix} \begin{matrix} b_{j, k} = \frac{W_{j} - k}{W_{j}} \frac{1}{1 - p_{b}} (p_{c})^{j} b_{0, 0} (10) \\ k \in [1, W_{0} - 1], j \in [1, m] \end{matrix} \end{matrix}$

在平稳分布中, 根据归一化条件, 可得初始状态b_{0, 0}如式(11)所示:

$\begin{matrix} \begin{matrix} b_{0, 0} = [2 (1 - p_{b}) (1 - p_{c}) (1 - 2 p_{c})] / \\ [2 (1 - {p_{c}}^{m + 1}) (1 - p_{b}) (1 - 2 p_{c}) + W_{0} (1 - \\ (2 p_{c})^{m' + 1}) (1 - p_{c}) - (1 - {p_{c}}^{m' + 1}) (1 - 2 p_{c}) + \\ {p_{c}}^{m' + 1} (2^{m'} W_{0} - 1) (1 - 2 p_{c}) (1 - {p_{c}}^{m - m'})] (11) \end{matrix} \end{matrix}$

任意退避阶段只有退避计数器值减为0时, 消息才能被发送。因此消息能被发送的概率τ 的表达式为式(12):

$\begin{matrix} \begin{matrix} τ = \overset{m}{\sum_{i = 0}} b_{i, 0} = b_{0, 0} \overset{m}{\sum_{i = 0}} {p_{c}}^{i} = \\ [2 (1 - p_{b}) (1 - {p_{c}}^{m + 1}) (1 - 2 p_{c})] / \\ [2 (1 - {p_{c}}^{m + 1}) (1 - p_{b}) (1 - 2 p_{c}) + W_{0} (1 - \\ (2 p_{c})^{m' + 1}) (1 - p_{c}) - (1 - {p_{c}}^{m' + 1}) (1 - 2 p_{c}) + \\ {p_{c}}^{m' + 1} (2^{m'} W_{0} - 1) (1 - 2 p_{c}) (1 - {p_{c}}^{m - m'})] (12) \end{matrix} \end{matrix}$

用τ _i表示站点内AC[i](i=0, 1, 2, 3)队列消息能被发送的概率, 其表达式如式(13)所示:

$\begin{matrix} \begin{matrix} τ_{i} = [2 (1 - p_{bi}) (1 - {p_{ci}}^{m_{i} + 1}) (1 - 2 p_{ci})] / \\ [2 (1 - {p_{ci}}^{m_{i} + 1}) (1 - p_{bi}) (1 - 2 p_{ci}) + W_{0, i} (1 - \\ (2 p_{ci})^{m'_{i} + 1}) (1 - p_{ci}) - (1 - {p_{ci}}^{m'_{i} + 1}) (1 - 2 p_{ci}) + \\ {p_{ci}}^{m'_{i} + 1} (2^{m'_{i}} W_{0, i} - 1) (1 - 2 p_{ci}) (1 - {p_{ci}}^{m_{i} - m'_{i}})] (13) \end{matrix} \end{matrix}$

由式(13)知, AC[i]队列中消息能被发送的概率与AC[i]的最小竞争窗口值、碰撞概率和信道忙概率有关。需再找出τ _i、p_ci、p_bi之间的其他关系式, 联立求解消息能被发送的概率和碰撞概率等。

若本站点内其他AC队列或其他站点同时有消息发送时, 消息间会产生碰撞。消息的内部碰撞依据消息优先级决定消息发送权, 高优先级消息继续发送, 低优先级消息则重传。与外部站点消息发生碰撞时, 无论优先级高低消息都需重传。用 $\begin{matrix} {P_{I}}_{i} \end{matrix}$ 表示AC[i]的内部碰撞概率, 则其表达式为^[13]:

$\begin{matrix} \{\begin{matrix} P_{I 3} = 0 \\ P_{I 2} = τ_{3} \\ P_{I 1} = 1 - (1 - τ_{3}) (1 - τ_{2}) \\ P_{I 0} = 1 - (1 - τ_{3}) (1 - τ_{2}) (1 - τ_{1}) \end{matrix} (14) \end{matrix}$

AC[i]队列消息发送概率σ _i的表达式为^[16]:

$\begin{matrix} \{\begin{matrix} σ_{3} = τ_{3} \\ σ_{2} = τ_{2} (1 - P_{I 2}) = τ_{2} (1 - τ_{3}) \\ σ_{1} = τ_{1} (1 - P_{I 1}) = τ_{1} (1 - τ_{3}) (1 - τ_{2}) \\ σ_{0} = τ_{0} (1 - P_{I 0}) = τ_{0} (1 - τ_{3}) (1 - τ_{2}) (1 - τ_{1}) \end{matrix} (15) \end{matrix}$

站点内消息的发送概率为:σ _total= $\begin{matrix} \overset{3}{\sum_{i = 0}} \end{matrix}$ σ _i, 因此消息的外部碰撞概率P_O为:

$\begin{matrix} P_{O} = 1 - (1 - σ_{total})^{N - 1} (16) \end{matrix}$

式中:N为站点总数量。

AC[i]消息发送时产生碰撞的概率为p_ci:

$\begin{matrix} p_{ci} = P_{Ii} + (1 - P_{Ii}) P_{O} (17) \end{matrix}$

执行退避过程时, 退避计数器的值在时隙内减少, 即信道空闲概率为1-p_bi, 其表达式为:

$\begin{matrix} \{\begin{matrix} p_{b 3} = 1 - (1 - σ_{total})^{N - 1} (1 - τ_{0}) (1 - τ_{1}) (1 - τ_{2}) \\ p_{b 2} = 1 - (1 - σ_{total})^{N - 1} (1 - τ_{0}) (1 - τ_{1}) (1 - τ_{3}) \\ p_{b 1} = 1 - (1 - σ_{total})^{N - 1} (1 - τ_{0}) (1 - τ_{2}) (1 - τ_{3}) \\ p_{b 0} = 1 - (1 - σ_{total})^{N - 1} (1 - τ_{1}) (1 - τ_{2}) (1 - τ_{3}) \end{matrix} (18) \end{matrix}$

将式(13)(17)(18)联立组成一个非线性方程组, 可求解出AC[i]的发送概率σ _i和碰撞概率p_ci。

2.3 归一化吞吐量

归一化吞吐量为时间段内数据帧成功发送的量。设P_idle为信道空闲即时隙内无消息发送的概率; P_Tr为时隙内至少有一个站点发送消息的概率; P_S_i为AC[i]消息成功发送即时隙内只有一个站点发送AC[i]消息的概率; P_Fail为由于碰撞导致消息发送失败即时隙内有两个或两个以上的站点同时发送消息的概率。则其表达式为:

$\begin{matrix} \{\begin{matrix} P_{idle} = (1 - σ_{total})^{N} \\ P_{Tr} = 1 - P_{idle} \\ P_{Si} = N \times σ_{i} \times (1 - σ_{total})^{N - 1} \\ P_{Fail} = 1 - P_{idle} - N \times σ_{total} \times (1 - σ_{total})^{N - 1} \end{matrix} (19) \end{matrix}$

设S_i为站点内AC[i]的归一化吞吐量, 则:

$\begin{matrix} S_{i} = \frac{P_{Si} \times T_{E [L_{i}]}}{P_{idle} \times T_{aSl otTime} + \overset{3}{\sum_{i = 0}} P_{Si} \times T_{Si} + P_{Fail} \times T_{Ci}} (20) \end{matrix}$

式中: $\begin{matrix} T_{E [L_{i}]} \end{matrix}$ 为传输AC[i]数据包所需时间。分母第一部分为信道空闲时间的均值; 第二部分为数据包成功发送的时间均值; 第三部分为数据包发送失败的时间均值。式(20)中T_S_i为消息成功发送的传输时延, T_C_i为消息间发生碰撞所持续的时间。其表达式为:

$\begin{matrix} \{\begin{matrix} T_{Si} = T_{AIFS [AC [i]]} + T_{Head} + T_{L_{i}} + δ + T_{SIFS} + \\ T_{ACK} + δ \\ T_{C i} = T_{AIFS [AC [i]]} + T_{Head} + T_{L_{i}^{*}} + δ \end{matrix} (21) \end{matrix}$

式中:T_Head为消息帧帧头的传输时间; $\begin{matrix} T_{L_{i}} \end{matrix}$ 为数据包的传输时间; δ 为传播时延; T_SIFS为SIFS的持续时间; T_ACK为ACK的传输时间; $\begin{matrix} T_{L_{i}^{*}} \end{matrix}$ 为碰撞时数据包最大传输时间。

2.4 丢包率

设P_Drop_i为站点内AC[i]队列的丢包率。若数据包第m次重传失败, 则该数据包将被丢弃造成丢包, 丢包率表达式为:

$\begin{matrix} P_{Dropi} = p_{ci}^{m_{i} + 1} (22) \end{matrix}$

2.5 时延分析

MAC层时延定义为:消息从成为AC队列的队首开始到接收站点成功接收到该帧为止的时间段, 由接入时延和传输时延组成。用T_D表示消息的时延, E[T_D_i]为AC[i]消息时延的均值, 表达式如下^[5]:

$\begin{matrix} \begin{matrix} E [T_{Di}] = \\ E [N_{i}] (E [B_{Di}] + T_{Ci} + T_{0}) + (E [B_{Di}] + T_{Si}) (23) \end{matrix} \end{matrix}$

式中:E[N_i]为AC[i]消息退避重传次数的均值, 其表达式为:

$\begin{matrix} E [N_{i}] = \overset{m}{\sum_{j = 0}} j p_{ci}^{j} (1 - p_{ci}) (24) \end{matrix}$

式(23)中:E[B_D_i]为AC[i]消息的退避时间, 该时间由两部分组成, 分别为:不挂起情况下, 退避计数器连续减少到0所持续的时间, 用X_i表示, 其期望表达式如式(25)所示; 检测到信道忙导致退避计数器挂起所等待的时间, 用F_R_i表示, 表达式如式(26)所示。

$\begin{matrix} \begin{matrix} E [X_{i}] = \overset{m_{i}}{\sum_{j = 0}} \overset{W_{j} - 1}{\sum_{k = 1}} k b_{j, k} = \\ [b_{0, 0} (W_{0, i}^{2} (1 - (4 p_{ci})^{m'_{i} + 1}) (1 - p_{ci}) + \\ 4^{m'_{i}} W_{0, i}^{2} (p_{ci}^{m'_{i} + 1} - p_{ci}^{m_{i} + 1}) (1 - 4 p_{ci}) - (1 - p_{ci}^{m_{i} + 1}) \\ (1 - 4 p_{ci}))] / [6 (1 - p_{bi}) (1 - 4 p_{ci}) (1 - p_{ci})] (25) \\ E [F_{Ri}] = E [N_{backi}] (\overset{3}{\sum_{j = 0}} P_{Sj} \times T_{Sj} + P_{Fail} \times T_{Ci}) (26) \end{matrix} \end{matrix}$

式中:E[ $\begin{matrix} {N_{back}}_{i} \end{matrix}$ ]为AC[i]的退避计数器在递减过程中被挂起的次数, 其表达式为^[5]:

$\begin{matrix} E [{N_{back}}_{i}] = \frac{E [X_{i}] p_{bi}}{1 - p_{bi}} (27) \end{matrix}$

AC[i]队列消息的退避时间为:

$\begin{matrix} E [{B_{D}}_{i}] = E [X_{i}] + E [{F_{R}}_{i}] (28) \end{matrix}$

T₀为消息发生碰撞时, 重新监听信道前所等待的时间, 在基本接入模式下其表达式为:

$\begin{matrix} T_{0} = T_{SIFS} + T_{ACK_timeout} (29) \end{matrix}$

3 结果分析

3.1 性能指标分析

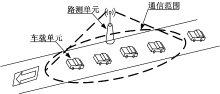
建立如图3所示的通信场景。联立求解得到归一化吞吐量、丢包率和时延性能指标, 并通过NS-2^[14]仿真验证了分析模型的准确性。计算中所需要参数的列表如下:数据包长度为512 bytes; 位传输速率为6 Mbit/s; 通信范围为500 m; 数据包产生量为10 packet/s; 短帧间间隔SIFS为32 μ s; 时隙时间slottime为13 μ s; 帧头传输时间Thead为57 μ s; ACK传输时间TACK为39 μ s; 传播时延δ 为2 μ s。

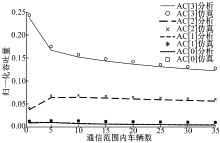
	Figure Option View Download New Window
	图3 通信场景Fig.3 Communication scenario

图4为不同AC队列的归一化吞吐量随通信范围内车辆数的变化情况。可见, 随着通信范围内车辆数的增加, AC队列的归一化吞吐量值逐渐减小。AC[3]队列的吞吐量最大, 而AC[0]最小。原因为发生内部冲突时, 虚拟调度器会选择高优先级消息发送, 造成低优先级消息重传。

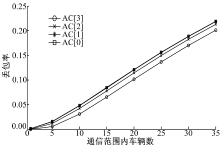
	Figure Option View Download New Window
	图4 归一化吞吐量随车辆数变化图Fig.4 Normalized throughput variation with number of vehicles

图5为不同AC队列的丢包率随通信范围内车辆数的变化情况。通过求解公式知, 丢包率只与碰撞概率有关。由图5可知, 不同AC队列的丢包率随车辆数的增加而上升。当通信范围内仅有一辆车时, AC[3]的丢包率为0, AC[0]的丢包率为1.3%, 该丢包是由于消息的内部碰撞造成的。随着通信范围内车辆数的增加, 消息碰撞加剧, 导致消息重传次数增加, 丢包现象加剧。当通信范围内有35辆车时, 4个AC的丢包率均超过了20%。为满足丢包率不超过10%^[3]的要求, 由图5知, 在饱和情况下通信范围内最大车辆数为19辆。

	Figure Option View Download New Window
	图5 丢包率随车辆数变化图Fig.5 Drop rate variation with number of vehicles

	Figure Option View Download New Window
	图6 时延随车辆数变化图Fig.6 Time delay variation with number of vehicles

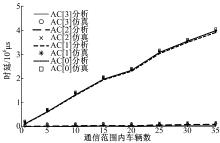
随着通信范围内车辆数的增加, 不同AC队列消息的时延也增加, 如图6所示。其中, 高优先级队列AC[3]和AC[2]队列的时延增加不明显, 而较低优先级队列AC[1]和AC[0]的时延急剧增加, 原因为高优先级消息发送的增加, 阻塞了低优先级发送, 从而导致时延增大。通信范围内车辆数为35时, AC[3]和AC[2]的时延均小于100 ms, 满足安全应用数据交互的时限要求^[12]。AC[1]和AC[0]可应用于非时间苛求类型的场合, 如娱乐等。

3.2 退避挂起机制对性能的影响

IEEE 802.11p协议规定退避时存在挂起机制。而很多文献采用Markov链分析时没予以考虑, 退避计数器的值以概率1递减, 即图2中p_b=0, 不存在D_i_,_j状态。所以研究退避挂起机制对网络性能(特别是对丢包率)的影响是必要的。

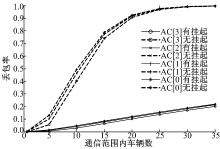
	Figure Option View Download New Window
	图7 退避挂起机制对丢包率的影响Fig.7 Effect of backoff mechanism on drop rate

图7为退避挂起机制对丢包率的影响。当通信范围内车辆数较少时, 退避挂起机制对改善丢包率无明显作用。但随着通信范围内车辆数的增加, 无退避挂起机制会导致丢包率的急剧上升。若无退避机制, 当通信范围内有19辆车时, 丢包率会达到90%以上, 而存在退避挂起机制时, 丢包率仅为10%。从而说明退避过程中采用挂起机制能有效地减少数据包碰撞概率, 从而降低丢包率。

4 结束语

本文考虑了不同类型消息间的影响, 在消息内部碰撞和信道忙时的退避挂起机制情况下, 采用二维Markov链对IEEE 802.11p的EDCA机制进行了建模。研究了归一化吞吐量、丢包率和时延性能指标, 并分析了退避挂起机制对丢包率的影响。结果表明:当通信范围内车辆数固定时, 单个站点的归一化吞吐量和时延与不同优先级AC队列有关; 丢包率只与AC队列和碰撞概率有关。而高优先级队列始终有较大吞吐量、较低时延和较小丢包率。通过分析得出为满足安全类应用丢包率的要求, 通信范围内的车辆数最多为19辆。同样也验证了IEEE 802.11p的EDCA机制能满足不同类型消息的服务质量。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Dar K, Bajhouya M, Gaber J, et al. Wireless communication technologies for ITS applications[J]. IEEE Communications Magazine, 2010, 48(5): 156-162. [本文引用:1]
[2]	IEEE Std. IEEE 802. 11p: Wireless LAN medium access control (MAC) and physical layer(PHY) specifications-amendment 7: wireless access in vehicular environment[S]. 2010. [本文引用:2]
[3]	IEEE 802. 11e/D6. 0. Draft supplement to part 11: Wireless medium access control(MAC) and physical layer specifications: medium access control (MAC) enhancement for quality of service (QoS)[S]. 2003. [本文引用:2]
[4]	Cheng H T, Shan H, Zhuang W. Infotainment and road safety service support in vehicular networking: From a communication perspective[C]∥Mech Syst Signal Process, 2011, 25(6): 2020-2038. [本文引用:1]
[5]	Bianchi G. Performance analysis of the IEEE 802. 11 distributed coordination function[J]. IEEE Journal on Selected Areas in Communications, 2000, 18(3): 535-547. [本文引用:3]
[6]	杨卫东, 李亚辉, 马建峰. 衰落信道中802. 11 DCF的非饱和吞吐量分析[J]. 吉林大学学报: 工学版, 2008, 38(3): 695-699. Yang Wei-dong, Li Ya-Hui, Ma Jian-feng. Non-saturation throughput analysis of 802. 11 DCF in fading channel[J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 38(3): 695-699. [本文引用:1]
[7]	Robinson J, Rand hawa T. Saturation throughput analysis of IEEE 802. 11e enhanced distributed coordination function[J]. IEEE Journal Selected Areas Communication, 2004, 22(5): 917-928. [本文引用:1]
[8]	Tursunova S, Kim Young-tak. Realistic IEEE 802. 11e EDCA model for QoS-aware mobile cloud service provisioning[J]. IEEE Transactions on Consumer Electronics, 2012, 58(1): 60-68. [本文引用:1]
[9]	Gas M, Kosek-saott K, Natkaniec M, et al. 3D Markov chain-based saturation throughput model of IEEE 802. 11 EDCA[J]. Electronics Letters, 2011, 47(14): 826-827. [本文引用:1]
[10]	Inan I, Keceli F, Ayanoglu E. Analysis of the 802. 11e enhanced distributed channel access function[J]. IEEE Transactions on Communications, 2009, 57(6): 1753-1764. [本文引用:1]
[11]	Yao Yuan, Rao Lei, Liu Xue. Performance and reliability analysis of IEEE 802. 11p safety communication in a highway environment[J]. IEEE Transactions on Vehicular Technology, 2013, 62(9): 4198-4212. [本文引用:1]
[12]	Han C, Dianati M, Tafazollir E, et al. Analytical study of the IEEE 802. 11p MAC sublayer in vehicular networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 99: 1-14. [本文引用:1]
[13]	Huang C L, Liao W. Throughput and delay performance of IEEE 802. 11e enhanced distributed channel access (EDCA) under saturation condition[J]. IEEE Transactions on Wireless Communications, 2007, 6(1): 136-145. [本文引用:1]
[14]	The Network Simulator-ns-2. [DB/OL][2014-06-21]. http://www.isi.edu/nsnam/ns/. [本文引用:1]

2010

0.0

... 0 引言车载自组网(Vehicular ad-hoc networks,VANETs)依靠先进的信息技术和通信技术为日益严重的交通问题,如道路拥堵和事故频发,提供了解决方案^[1] ...

2010

0.0

... 11p^[2]作为底层协议以解决车辆环境下的无线接入问题,如车辆高速移动导致的通信拓扑频繁变换及不同应用类型通信性能的不同需求等 ...

... AC[i](i=0,1,2,3)的T_AIFS[AC[_i_]]计算公式如下^[2]: ...

2003

0.0

... 11e^[3]的增强型分布信道访问(Enhanced distributed channel access,EDCA)机制以提供多种应用类型的服务,然而不同类型的服务质量(Quality of service,QoS)要求不同,如安全类应用实时性要求较高^[4] ...

... 为满足丢包率不超过10%^[3]的要求,由图5知,在饱和情况下通信范围内最大车辆数为19辆 ...

2011

0.0

2000

0.0

... 其中大部分是对Bianchi模型^[5]的改进,如文献[6]对DCF(Distributed coordination function)的非饱和吞吐量进行了计算 ...

... 用T_D表示消息的时延,E[T_D_i]为AC[i]消息时延的均值,表达式如下^[5]: ...

... 式中:E[ Nbacki]为AC[i]的退避计数器在递减过程中被挂起的次数,其表达式为^[5]: ...

2008

0.0

. 2008, 38(3):695-699

Non-saturation throughput analysis of 802.11 DCF in fading channel

衰落信道中802.11 DCF的非饱和吞吐量分析

Yang Wei-dong , Li Ya-Hui , Ma Jian-feng.

杨卫东, 李亚辉, 马建峰

Key Laboratory of Computer Network and Information Security，Ministry of Education, Xidian University, Xi'an 710071, China

Using a three dimensional Markov chain, a nonsaturation throughput performance model was proposed for IEEE 802.11 Distributed Coordination Function (DCF) in fading channel. The impacts of different factors, including bit error ratio, traffic loads and packet length, on the throughput of the system were analyzed using this model. Based on the model, a simple formula was derived to calculate the optimized packet length for maximizing the nonsaturation throughput. Simulation results show that this model can effectively predict the nonsaturation throughput of 802.11 DCF in fading channel, and by employing the optimum packet length the system throughput can be enhanced.

利用时间离散的三维马尔可夫链，建立了衰落信道中IEEE 802.11 DCF（分布式协调功能）在非饱和状态下的吞吐量性能模型，分析了位错误率、传输负载和分组长度对系统吞吐量的影响。基于该模型，推导了根据信道质量，计算分组长度最优值的简单公式。仿真结果表明，模型能够有效地预测802.11 DCF在衰落信道下的非饱和吞吐量，采用最优分组长度可以提高系统吞吐量。

2004

0.0

2012

0.0

2011

0.0

2009

0.0

2013

0.0

2012

0.0

... 通信范围内车辆数为35时,AC[3]和AC[2]的时延均小于100 ms,满足安全应用数据交互的时限要求^[12] ...

2007

0.0

... 用 PIi表示AC[i]的内部碰撞概率,则其表达式为^[13]: ...

2014

0.0

... 联立求解得到归一化吞吐量、丢包率和时延性能指标,并通过NS-2^[14]仿真验证了分析模型的准确性 ...