基于质心参照拓扑的灰色航迹抗差关联算法

引用本文

董凯, 刘瑜, 王海鹏. 基于质心参照拓扑的灰色航迹抗差关联算法. 2015, 45(4): 1311-1317
DONG Kai, LIU Yu, WANG Hai-peng. Grey track anti-bias association algorithm based on centroid topology of reference. Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1311-1317 复制到剪切板

Permissions

基于质心参照拓扑的灰色航迹抗差关联算法

董凯, 刘瑜, 王海鹏

海军航空工程学院信息融合研究所, 山东烟台 264001

作者简介:董凯(1986-),男,博士研究生.研究方向:多源信息融合.E-mail:188dongkai@163.com

基金:国家自然科学基金重点项目(61032001); 山东省自然科学基金项目(ZR2012FQ004)

摘要

针对传感器系统误差影响下利用目标拓扑信息的航迹关联算法性能受参照目标状态估计精度制约的问题,提出了一种基于质心参照拓扑的灰色航迹抗差关联算法。该算法以传感器共同观测目标的融合质心位置和航向为参照,建立目标拓扑描述向量,然后采用序贯修正的灰色关联分析方法计算各传感器航迹间的灰关联度,最后以灰关联度为检验统计量进行全局最优的航迹抗差关联判决。仿真结果表明,在随机交叉目标和密集平行编队环境下,该算法的性能和稳健性明显优于传统方法。

关键词: 通信技术; 航迹关联; 系统误差; 参照拓扑; 灰关联度; 抗差关联

中图分类号:TN957 文献标志码:A 文章编号:1671-5497(2015)04-1311-07

Grey track anti-bias association algorithm based on centroid topology of reference

DONG Kai, LIU Yu, WANG Hai-peng

Institute of Information Fusion, Naval Aeronautical and Astronautical University, Yantai 264001, China

Abstract

The performance of tracking association algorithm using target topology information is influenced by the estimation accuracy of the reference target state because of sensor bias. To solve such problem, a grey track anti-bias association algorithm based on centroid topology of reference is proposed. First, the algorithm takes the position and course of the sensor commonly observed targets' fusion centroid as the reference, and constructs the target topological vector. Then, the subsequential modified grey association analysis algorithm is used to calculate the grey association degree of the sensors. Finally, the global optimal track anti-bias association is carried out using the grey association degree as test statistical vector. Simulation results show that the performance and robustness of the proposed algorithm are better than the traditional algorithm apparently in random cross targets and dense parallel formation environment.

Keyword: communication; track association; system bias; topology of reference; grey association degree; anti-bias association

Show Figures

0 引言

分布式多传感器航迹融合的前提是航迹关联, 其含义是判断不同传感器的两条航迹是否代表同一个目标的过程^[1]。在传统的分布式航迹关联算法研究中, 通常假定传感器不存在系统误差。在实际工程应用中, 传感器不可避免存在距离、方位角、俯仰角测量的系统误差, 系统误差使传感器的观测航迹整体偏离目标真实轨迹, 因此依靠各传感器航迹间相对位置信息进行航迹关联判断的算法^{[2, 3]}适用性大大降低。

针对传感器存在系统误差条件下的航迹关联问题(本文称之为航迹抗差关联问题), 文献[4]首先提出利用观测目标参照拓扑信息, 采用扇形格和弥散化系数量化拓扑结构, 然后采用模糊模式识别方法进行航迹关联; 文献[5]选择三角形作为拓扑结构元, 用边长构造归一化拓扑相似度, 没有利用目标的相对角度信息, 降低了目标密集环境下的可靠性; 文献[6]考虑目标丢失的情况, 采用松弛迭代的方法实现区域目标的最大匹配, 但要求目标分布区域较小和方位系统误差较小, 并且只利用了目标之间的距离信息; 文献[7]分局部特征和全局特征对编队目标结构进行描述, 局部特征描述以三角形为结构元, 全局特征描述以编队重心为参照计算目标结构特征量, 并针对两种方法的优缺点提出层次化匹配关联算法, 但在平行等间距编队目标情形下存在关联模糊; 文献[8]应用灰色理论构建传感器航迹的局部自相关矩阵, 然后进行航迹关联判决的方法, 但没有给定拓扑目标的排列顺序, 关联结果存在不确定性; 文献[9]考虑传感器的方位系统误差, 以目标航向为基准划分多象限, 建立各象限内目标位置径向距离和拓扑向量、航速欧式距离和航向变化率3个模糊因素集, 进行模糊航迹对准关联, 但目标估计航向值的随机扰动(例如目标机动时滤波精度降低)将使算法性能大大降低。针对参照目标精度影响航迹抗差关联的问题, 本文提出一种基于质心参照拓扑的灰色航迹抗差关联算法, 与传统拓扑方法的主要区别在于:①利用航迹数据中的状态估计协方差信息, 计算观测区域目标的融合质心; ②以融合质心位置及航向建立参照系进行目标拓扑描述, 比目标参照系^[9]的精度和稳定性更高; ③利用航迹历史信息和灰色关联分析方法^[10], 对各传感器航迹拓扑描述向量进行关联匹配。最后根据航迹灰关联度矩阵进行全局最优的航迹抗差关联判决。

1 质心参照拓扑模型

1.1 系统误差影响分析

通常认为传感器系统误差为较小常量或者长时间范围内的缓变量, 因此在较短观测时间内可视为常量。设真实目标的距离和方位分别为r和θ , 不考虑随机量测误差时, 传感器方位和距离系统误差分别使目标观测值偏离Δ θ 角度和Δ r距离, 即在系统误差影响下, 所有目标的观测值在传感器极坐标系下相对目标真实位置发生Δ θ 的旋转和Δ r的伸缩。文献[9]的推导表明, 当目标观测区域距离传感器较远时(Δ r/r≪1), 可忽略系统误差引起的仿射变换, 近似认为传感器的系统误差不改变各目标之间的相对位置关系, 即一部传感器的航迹经过整体旋转和平移后能够与另一部传感器的航迹重合。从而为利用目标拓扑信息实现航迹关联提供了可能。

1.2 融合质心参照系的建立

假设m部传感器对共同观测区域内的目标探测概率为1, 选取各传感器共同观测的n个目标, 分别计算观测目标的融合质心状态估计。设 $\begin{matrix} {\hat{X}}_{s}^{i} \end{matrix}$ (k $\begin{matrix} |k \end{matrix}$ )和 $\begin{matrix} P_{s}^{i} \end{matrix}$ (k $\begin{matrix} |k \end{matrix}$ )分别为传感器s在k时刻对目标i的状态估计值及其状态估计协方差(i=1, 2, …, n; s=1, 2, …, m)。通常认为传感器对各目标的状态估计统计独立, 因此可以采用加权融合算法实时计算传感器s观测区域目标的质心状态估计 $\begin{matrix} {\hat{X}}_{s}^{0} \end{matrix}$ (k $\begin{matrix} |k \end{matrix}$ )及其估计协方差 $\begin{matrix} P_{s}^{0} \end{matrix}$ (k $\begin{matrix} |k \end{matrix}$ )。

$\begin{matrix} \begin{matrix} {\hat{X}}_{s}^{0} (k |k) = P_{s}^{0} (k |k) \overset{n}{\sum_{i = 1}} P_{s}^{i} {(k |k)}^{- 1} {\hat{X}}_{s}^{i} (k |k) (1) \\ P_{s}^{0} (k |k) = {[\overset{n}{\sum_{i = 1}} P_{s}^{i} {(k |k)}^{- 1}]}^{- 1} (2) \end{matrix} \end{matrix}$

式中:

$\begin{matrix} {\hat{X}}_{s}^{i} \end{matrix}$ (k $\begin{matrix} |k \end{matrix}$ )=[ $\begin{matrix} {\hat{x}}_{s}^{i} \end{matrix}$ (k) $\begin{matrix} {\hat{\overset{\cdot}{x}}}_{s}^{i} \end{matrix}$ (k) $\begin{matrix} {\hat{y}}_{s}^{i} \end{matrix}$ (k) $\begin{matrix} {\hat{\overset{\cdot}{y}}}_{s}^{i} \end{matrix}$ (k)]' (3)

从而可以得到加权融合的区域目标质心坐标( $\begin{matrix} {\hat{x}}_{s}^{0} \end{matrix}$ (k), $\begin{matrix} {\hat{y}}_{s}^{0} \end{matrix}$ (k))和航向 $\begin{matrix} θ_{s}^{0} \end{matrix}$ (k)(以正北为基准)。

$\begin{matrix} \begin{matrix} θ_{s}^{0} (k) = \\ \{\begin{matrix} \arctan ({\hat{\overset{\cdot}{x}}}_{s}^{0} (k) / {\hat{\overset{\cdot}{y}}}_{s}^{0} (k)), {\hat{\overset{\cdot}{y}}}_{s}^{0} (k) \geq 0 \\ \arctan ({\hat{\overset{\cdot}{x}}}_{s}^{0} (k) / {\hat{\overset{\cdot}{y}}}_{s}^{0} (k)) - π, {\hat{\overset{\cdot}{x}}}_{s}^{0} (k) \geq 0, {\hat{\overset{\cdot}{y}}}_{s}^{0} (k) < 0 \\ \arctan ({\hat{\overset{\cdot}{x}}}_{s}^{0} (k) / {\hat{\overset{\cdot}{y}}}_{s}^{0} (k)) + π, {\hat{\overset{\cdot}{x}}}_{s}^{0} (k) < 0, {\hat{\overset{\cdot}{y}}}_{s}^{0} (k) < 0 \end{matrix} (4) \end{matrix} \end{matrix}$

需注意, ( $\begin{matrix} {\hat{x}}_{s}^{0} \end{matrix}$ (k), $\begin{matrix} {\hat{y}}_{s}^{0} \end{matrix}$ (k))和 $\begin{matrix} θ_{s}^{0} \end{matrix}$ (k)是在传感器局部坐标系下通过加权融合得到的估计值, 分别隐含传感器的距离和方位角测量系统误差。

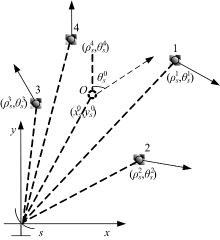
图1给出了k时刻传感器观测n个(n=4)目标在传感器局部坐标系下的整体态势, 图中 $\begin{matrix} ρ_{s}^{i} \end{matrix}$ 和 $\begin{matrix} θ_{s}^{i} \end{matrix}$ 分别表示在传感器局部坐标系下传感器对目标i(i=1, 2, 3, 4)跟踪航迹在k时刻的距离和方位估计值, 各目标箭头方向表示其运动方向。o表示k时刻区域目标融合质心, $\begin{matrix} θ_{s}^{0} \end{matrix}$ 表示质心运动方位角, 箭头方向表示质心运动方向。建立以区域目标质心位置为坐标原点, 质心航向为x轴正向的区域目标质心参照系对目标进行描述, 可以很大程度上抵消系统误差。经过旋转和平移操作, 得到图2所示的质心参照系下目标拓扑结构示意图, 图中 $\begin{matrix} ρ_{o}^{i} \end{matrix}$ 和 $\begin{matrix} θ_{o}^{i} \end{matrix}$ 分别表示在质心参照坐标系下目标i的距离和方位值, 各目标箭头方向表示其运动方向。对比可见各目标的速度方向均相对传感器局部坐标系下的方向顺时针旋转了 $\begin{matrix} θ_{s}^{0} \end{matrix}$ 角度, 坐标位置平移了( $\begin{matrix} x_{s}^{0} \end{matrix}$ , $\begin{matrix} y_{s}^{0} \end{matrix}$ ), 相对质心的位置和方位没有改变。

	Figure Option View Download New Window
	图1 传感器局部坐标系下目标分布Fig.1 Target distribution in sensor’ s local coordinate

	Figure Option View Download New Window
	图2 质心参照系下目标拓扑结构Fig.2 Targets’ topology in centroid reference coordinate

与以往的目标参照拓扑法中以各个目标为参照相比, 加权融合质心比单一目标具有更高的位置和航向精度, 因而能够为不同传感器的目标提供更为准确的参照拓扑描述, 为算法性能的提高做了重要铺垫。

1.3 目标拓扑描述向量

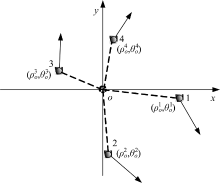
建立区域目标质心参照系之后, 就可以对目标的状态进行拓扑描述。虽然在系统误差影响下各传感器的区域目标质心参照系并不重合, 但目标在不同质心参照系下径向距离和方位是近似不变的(存在随机误差)。此外, 目标速度大小与参照系的选择无关, 运动方向在质心参照系下同样是近似不变的, 因此本文选择上述4个不变信息量构建各传感器目标的拓扑描述向量。区域目标i在质心o参照系下的拓扑描述向量 $\begin{matrix} T_{o}^{i} \end{matrix}$ (k)如下:

$\begin{matrix} T_{o}^{i} (k) = [ρ_{o}^{i} (k) θ_{o}^{i} (k) λ_{o}^{i} (k) β_{o}^{i} (k)]' (5) \end{matrix}$

式中: $\begin{matrix} λ_{o}^{i} \end{matrix}$ (k)为目标估计速度值; $\begin{matrix} β_{o}^{i} \end{matrix}$ (k)为目标在质心参照坐标系下的估计速度方位角, 它是目标估计速度在传感器局部坐标系下的速度方位角 $\begin{matrix} β_{s}^{i} \end{matrix}$ (k)相对 $\begin{matrix} θ_{s}^{0} \end{matrix}$ (k)的顺时针方向的夹角, 取值范围为0~2π 。

$\begin{matrix} \begin{matrix} ρ_{o}^{i} (k) = \sqrt[]{({\hat{x}}_{s}^{i} (k) - {\hat{x}}_{s}^{0} {(k))}^{2} + ({\hat{y}}_{s}^{i} (k) - {\hat{y}}_{s}^{0} {(k))}^{2}} (6) \\ θ_{o}^{i} (k) = \{\begin{matrix} θ_{s}^{i} (k) - θ_{s}^{0} (k), θ_{s}^{i} (k) \geq θ_{s}^{0} (k) \\ θ_{s}^{i} (k) - θ_{s}^{0} (k) + 2 π, θ_{s}^{i} (k) < θ_{s}^{0} (k) \end{matrix} (7) \\ θ_{s}^{i} (k) = \\ \{\begin{matrix} \arctan ({\hat{x}}_{s}^{i} (k) / {\hat{y}}_{s}^{i} (k)), {\hat{y}}_{s}^{i} (k) \geq 0 \\ \arctan ({\hat{x}}_{s}^{i} (k) / {\hat{y}}_{s}^{i} (k)) - π, {\hat{x}}_{s}^{i} (k) \geq 0, {\hat{y}}_{s}^{i} (k) < 0 \\ \arctan ({\hat{x}}_{s}^{i} (k) / {\hat{y}}_{s}^{i} (k)) + π, {\hat{x}}_{s}^{i} (k) < 0, {\hat{y}}_{s}^{i} (k) < 0 \end{matrix} (8) \\ λ_{o}^{i} (k) = \sqrt[]{{\hat{\overset{\cdot}{x}}}_{s}^{i} {(k)}^{2} + {\hat{\overset{\cdot}{y}}}_{s}^{i} {(k)}^{2}} (9) \\ β_{o}^{i} (k) = \{\begin{matrix} β_{s}^{i} (k) - θ_{s}^{0} (k), β_{s}^{i} (k) \geq θ_{s}^{0} (k) \\ β_{s}^{i} (k) - θ_{s}^{0} (k) + 2 π, β_{s}^{i} (k) < θ_{s}^{0} (k) \end{matrix} (10) \\ β_{s}^{i} (k) = \\ \{\begin{matrix} \arctan ({\hat{\overset{\cdot}{x}}}_{s}^{i} (k) / {\hat{\overset{\cdot}{y}}}_{s}^{i} (k)), {\hat{\overset{\cdot}{y}}}_{s}^{i} (k) \geq 0 \\ \arctan ({\hat{\overset{\cdot}{x}}}_{s}^{i} (k) / {\hat{\overset{\cdot}{y}}}_{s}^{i} (k)) - π, {\hat{\overset{\cdot}{x}}}_{s}^{i} (k) \geq 0, {\hat{\overset{\cdot}{y}}}_{s}^{i} (k) < 0 \\ \arctan ({\hat{\overset{\cdot}{x}}}_{s}^{i} (k) / {\hat{\overset{\cdot}{y}}}_{s}^{i} (k)) + π, {\hat{\overset{\cdot}{x}}}_{s}^{i} (k) < 0, {\hat{\overset{\cdot}{y}}}_{s}^{i} (k) < 0 \end{matrix} (11) \end{matrix} \end{matrix}$

为简化算法描述, 以两部传感器(s=1, 2)为例进行讨论, 同理可得传感器2的区域目标j在质心o'参照系下的拓扑描述向量 $\begin{matrix} T_{o'}^{j} \end{matrix}$ (k)如下:

$\begin{matrix} T_{o'}^{j} (k) = [ρ^{j} (k) θ^{j} (k) λ^{j} (k) β^{j} (k)]' (12) \end{matrix}$

2 序贯修正灰色航迹抗差关联

2.1 序贯修正灰关联度

传感器1和传感器2的拓扑数据列分别表示为T_o(k)= $\begin{matrix} \{T_{o}^{i} (k) |i = 1, 2, \dots, n\} \end{matrix}$ 和T_o'(k)= $\begin{matrix} \{T_{o'}^{j} (k) |j = 1, 2, \dots, n\} \end{matrix}$ , 二者的灰关联系数计算如下:

$\begin{matrix} \begin{matrix} ξ_{ij} (k, l) = \frac{\min_{i} \min_{j} Δ_{ij} (k, l) + ρ \max_{i} \max_{j} Δ_{ij} (k, l)}{Δ_{ij} (k, l) + ρ \max_{i} \max_{j} Δ_{ij} (k, l)} (13) \\ Δ_{ij} (k, l) = \{\begin{matrix} |ρ_{o}^{i} (k) - ρ_{o'}^{j} (k)|, l = 1 \\ |θ_{o}^{i} (k) - θ_{o'}^{j} (k)|, l = 2 \\ |λ_{o}^{i} (k) - λ_{o'}^{j} (k)|, l = 3 \\ |β_{o}^{i} (k) - β_{o'}^{j} (k)|, l = 4 \end{matrix} (14) \end{matrix} \end{matrix}$

式中:l=1, 2, 3, 4为描述向量中的指标序号; ρ 为分辨系数, ρ 越小, 分辨力越大, 一般取ρ =0.5; $\begin{matrix} \min_{i} \end{matrix} \begin{matrix} \min_{j} \end{matrix}$ Δ _ij(k, l)为两级最小差; $\begin{matrix} \max_{i} \end{matrix} \begin{matrix} \max_{j} \end{matrix}$ Δ _ij(k, l)为两级最大差; Δ _ij(k, l)为第l个指标量的绝对差。需注意, 指标2和指标4计算的角度差与指标1和指标3计算的距离差不同, 角度差是向量夹角, 相减时需进行角度周期性修正。

从式(14)可以看出, 指标绝对差的计算是在单个时刻数据列之间进行的, 没有利用航迹的历史信息, 因此本文借鉴文献[11]中序贯航迹关联思想, 把航迹当前时刻与其历史时刻联系起来, 对指标绝对差进行序贯累积, 得到修正的指标绝对差Δ '_ij(k, l)如下:

Δ '_ij(k, l)=Δ '_ij(k-1, l)+Δ _ij(k, l) (15)

需要注意的是, 虽然 $\begin{matrix} Δ_{ij}^{'} \end{matrix}$ (k, l)随时间推进不断增大, 但能使后续时刻的灰关联系数取值范围保持在0~1区间, 而利用航迹历史数据的指标绝对差信息有利于提高航迹抗差关联算法的性能。

然后对数据列各个指标的关联系数求加权平均, 得到k时刻拓扑描述向量 $\begin{matrix} T_{o}^{i} \end{matrix}$ (k)和 $\begin{matrix} T_{o'}^{j} \end{matrix}$ (k)之间的序贯修正灰关联度γ _ij(k)如下:

$\begin{matrix} γ_{ij} (k) = \overset{4}{\sum_{l = 1}} ξ_{ij} (k, l) \cdot a (l) (16) \end{matrix}$

式中:a(l)为指标l的权系数, 且 $\begin{matrix} \overset{4}{\sum_{l = 1}} \end{matrix}$ a(l)=1, a(l)≥ 0, 表明l对判决的重要程度。由此构建k时刻传感器1和传感器2航迹灰关联度矩阵:

γ (k)= $\begin{matrix} [\begin{matrix} γ_{11} (k) & γ_{12} (k) & \dots & γ_{1 n} (k) \\ γ_{21} (k) & γ_{22} (k) & \dots & γ_{2 n} (k) \\ ⋮ & ⋮ & ⋮ \\ γ_{n 1} (k) & γ_{n 2} (k) & \dots & γ_{nn} (k) \end{matrix}] \end{matrix}$ (17)

2.2 全局最优关联判决

根据两部传感器航迹的灰关联度矩阵建立以γ _ij(k)为统计量, L(k)为目标函数的二维分配模型^{[12, 13]}, 求解全局最优的航迹关联关系:

$\begin{matrix} \begin{matrix} L (k) = \min_{η_{ij}} \overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} η_{ij} γ_{ij} (k) (18) \\ s.t. \overset{n}{\sum_{j = 1}} η_{ij} = 1, \forall i = 1, 2, \dots, n (19) \\ \overset{n}{\sum_{i = 1}} η_{ij} = 1, \forall j = 1, 2, \dots, n (20) \end{matrix} \end{matrix}$

式中:η _ij为二进制变量, η _ij=1表示航迹i和航迹j来自于同一目标; η _ij=0则表示来自于不同目标。二维分配处理得到的关联对再经过灰关联度门限ε (0.5≤ ε < 1)的检验, 即灰关联度高于门限的关联对才被确认为航迹关联对。ε 的取值可通过仿真确定。

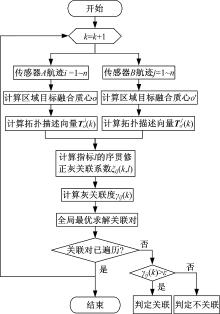
将该问题推广为多局部节点的航迹关联问题时, 可参考文献[14]中的全局统计量, 建立多维分配模型, 采用拉格朗日松弛算法求解, 这里不再赘述。图3给出了算法流程图。

	Figure Option View Download New Window
	图3 算法流程图Fig.3 Flow chart of algorithm

3 仿真验证

3.1 仿真环境

为验证算法的性能, 对本文提出的质心参照法和文献[9]中的拓扑模糊法进行50次步长为12的蒙特卡洛仿真, 给出算法的航迹抗差正确关联率和错误关联率结果。设两部传感器坐标分别为(100, 100) km和(200, 100) km, 测距误差均为100 m, 测角误差均为0.3° , 测距系统误差均为100 m, 测角系统误差均为3° , 采样周期为4 s, 灰关联度门限ε =0.6, 分辨系数ρ =0.5, 指标权系数a=[0.4, 0.4, 0.1, 0.1], 设置2种仿真环境。

环境1:随机交叉目标是航迹关联算法研究中的一种典型环境^[1], 设目标数30, 目标初始位置在(0, 300)km与(0, 200)km之间按正态分布产生, 初速和初始航向分别在4~220 m/s和0~2π 区间均匀分布。

环境2:平行编队目标是航迹关联算法研究中的另一种典型环境^[15], 设目标数10, 第一个目标初始位置为(130, 120) km, 相邻目标间隔300 m, 初始速度为400 m/s, 初始航向为30° (以正北为基准)。

3.2 仿真结果及分析

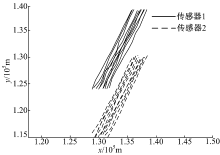
图4为环境1下两部传感器的观测航迹, 图5为环境2下两部传感器的观测航迹。可见在系统误差影响下, 两部传感器的航迹均出现了较大偏差。

	Figure Option View Download New Window
	图4 两部传感器的观测航迹(环境1)Fig.4 Tracks of 2 sensors(case 1)

	Figure Option View Download New Window
	图5 两部传感器的观测航迹(环境2)Fig.5 Tracks of 2 sensors(case 2)

	Figure Option View Download New Window
	图6 航迹正确关联率(环境1)Fig.6 Correct track association ratio(case 1)

	Figure Option View Download New Window
	图7 航迹错误关联率(环境1)Fig.7 False track association ratio(case 1)

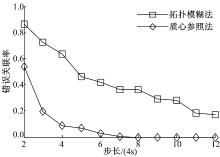
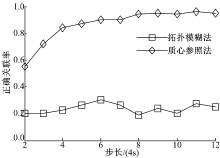
图6、图7分别为环境1下算法的航迹正确关联率和错误关联率比较图, 可见质心参照法的性能明显优于拓扑模糊法, 并且随步长推进, 目标密集程度逐步降低, 正确关联率逐步提高。主要原因是拓扑模糊法对每个目标建立参照拓扑信息, 而不同传感器对同一目标的航向估计值受滤波随机误差影响而存在差异, 导致不同传感器对同一目标建立的参照系之间存在随机旋转角, 降低了目标参照拓扑信息的匹配程度, 从而影响了算法性能。即只有当目标滤波稳定, 航向估计精度很高时才能保持较高的正确关联率, 如果由目标机动等原因导致滤波误差增大, 模糊拓扑法的性能将难以保证。相比之下, 质心参照法在加权融合算法的基础上建立质心参照系, 质心的坐标值和质心航向估计值均具有更高的精度和稳定度, 不同传感器在此参照系上构建的参照拓扑描述向量具备更高的匹配度, 从而使算法能够稳定保持更高的正确关联率。此外, 所采用的序贯修正灰关联度进一步提升了算法性能。

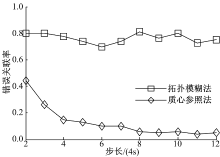
图8、图9分别为环境2下算法的航迹正确关联率和错误关联率比较图, 可见拓扑模糊法的性能较差, 并且在仿真时间段内没有显著变化, 主要原因有:①编队目标的速度和航向等运动特性相似, 导致拓扑模糊法中的速度和航向两个模糊因素失去辅助关联判决的作用; ②编队目标集中于根据算法要求划分的参照目标部分象限分界线附近, 在随机误差影响下其相对拓扑向量的准确性大大降低, 导致正确关联率较低; ③编队目标平行运动期间, 目标密集程度、拓扑结构变化不大。而质心参照法由于利用了航迹历史信息计算航迹间序贯修正灰关联度, 随步长推进能够持续提高正确关联率。

	Figure Option View Download New Window
	图8 航迹正确关联率(环境2)Fig.8 Correct track association ratio(case 2)

	Figure Option View Download New Window
	图9 航迹错误关联率(环境2)Fig.9 False track association ratio(case 2)

4 结束语

本文对系统误差影响下的分布式多传感器航迹关联问题展开了研究, 提出一种基于质心参照拓扑的灰色航迹抗差关联算法。首先建立加权融合质心参照系以获得更为准确、稳定的目标拓扑描述, 然后利用参照系下4种与系统误差无关的匹配信息构建目标拓扑描述向量, 再计算各传感器航迹之间的序贯修正灰关联度矩阵, 最后进行全局最优的航迹关联判决。两种典型仿真环境下的仿真结果表明, 在传感器存在系统误差的条件下, 本文算法在关联正确率和环境适应性上表现出良好的抗差关联效果, 能够为误差配准提供可靠的航迹关联对。由于算法需要各传感器完全探测共同观测区域内的目标, 以保证目标拓扑结构的完整性, 因此对干扰环境下传感器存在虚假航迹和错误航迹的复杂情形适应性有所不足, 这也是需要进一步研究的内容。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	何友, 王国宏, 陆大金, 等. 多传感器信息融合及应用[M]. 2版. 北京: 电子工业出版社, 2007: 51-52. [本文引用:2]
[2]	Mori S, Chang K C, Chong C Y. Comparison of track fusion rules and track association metrics[C]∥The 15th International Conference on Information Fusion, Singapore, 2012: 1996-2003. [本文引用:1]
[3]	Khaleghi B, Khamis A, Karray F, et al. Multisensor data fusion: a review of the state-of-the-art[J]. Information Fusion, 2013, 14: 28-44. [本文引用:1]
[4]	石玥, 王钺, 王树刚, 等. 基于目标参照拓扑的模糊航迹关联方法[J]. 国防科技大学学报, 2006, 28(4): 105-109. Shi Yue, Wang Yue, Wang Shu-gang, et al. Fuzzy data association based on target topology of reference[J]. Journal of National University of Defense Technology, 2006, 28(4): 105-109. [本文引用:1]
[5]	杨哲, 韩崇昭, 李晨, 等. 基于目标之间拓扑信息的数据关联方法[J]. 系统仿真学报, 2008, 20(9): 2357-2360. Yang Zhe, Han Chong-zhao, Li Chen, et al. Data association based on target topology[J]. Journal of System Simulation, 2008, 20(9): 2357-2360. [本文引用:1]
[6]	吴泽民, 邱正伦, 任姝婕. 多传感器航迹相关的区域匹配算法[J]. 弹箭与制导学报, 2011, 31(4): 210-213. Wu Ze-min, Qiu Zheng-lun, Ren Shu-jie. Area matching algorithm for multi-sensor track correlation[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2011, 31(4): 210-213. [本文引用:1]
[7]	曾昊. 基于星载异类传感器的舰船编队目标数据关联方法研究[D]. 长沙: 国防科学技术大学, 2008. Zeng Hao. Data association research about targets among ship formation based on heterogeneous space borne reconnaissance sensors[D]. Changsha: National University of Defense Technology, 2008. [本文引用:1]
[8]	方亮. 系统偏差条件下的航迹相关技术研究[D]. 长沙: 国防科学技术大学, 2009. Fang Liang. Research on track correlation with system bias[D]. Changsha: National University of Defense Technology, 2009. [本文引用:1]
[9]	宋强, 熊伟, 马强. 基于目标不变信息量的模糊航迹对准关联算法[J]. 系统工程与电子技术, 2011, 33(1): 190-195. Song Qiang, Xiong Wei, Ma Qiang. Fuzzy track alignment-correlation algorithm based on target invariable information[J]. Systems Engineering and Electronics, 2011, 33(1): 190-195. [本文引用:1]
[10]	刘思峰, 党耀国, 方志耕. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2004: 50-75. [本文引用:1]
[11]	He You, Zhang Jing-wei. New track correlation algorithms in a multisensor data fusion system[J]. IEEE Transactions on Aerospace and Electronic System, 2006, 42(4): 1359-1371. [本文引用:1]
[12]	Liu Xi, Yin Hao, Tian Chang, et al. An improved 2-d assignment algorithm for track-to-track association[C]∥Control and Decision Conference, Guiyang, China, 2013: 3698-3703. [本文引用:1]
[13]	Kragel B, Herman S, Roseveare N. A comparison of methods for estimating track-to-track assignment probabilities[J]. IEEE Transactions on Aerospace and Electronic System, 2012, 48(3): 1870-1888. [本文引用:1]
[14]	熊伟, 张晶炜, 何友. 基于多维分配和灰色理论的航迹关联算法[J]. 电子与信息学报, 2010, 32(4): 898-901. Xiong Wei, Zhang Jing-wei, He You. Track correlation algorithm based on multi-dimension assignment and grey theory[J]. Journal of Electronics & Information Technology, 2010, 32(4): 898-901. [本文引用:1]
[15]	鹿传国, 冯新喜, 孔云波, 等. 基于图的分布式平飞航迹关联算法[J]. 电光与控制, 2012, 19(10): 30-33. Lu Chuan-guo, Feng Xin-xi, Kong Yun-bo, et al. Distributed formation-flying track-to-track association based on the graph[J]. Electronics Optics and Control, 2012, 19(10): 30-33. [本文引用:1]

2007

0.0

... 0 引言分布式多传感器航迹融合的前提是航迹关联,其含义是判断不同传感器的两条航迹是否代表同一个目标的过程^[1] ...

... 环境1:随机交叉目标是航迹关联算法研究中的一种典型环境^[1],设目标数30,目标初始位置在(0,300)km与(0,200)km之间按正态分布产生,初速和初始航向分别在4~220 m/s和0~2#cod#x003c0 ...

2012

0.0

... 在实际工程应用中,传感器不可避免存在距离、方位角、俯仰角测量的系统误差,系统误差使传感器的观测航迹整体偏离目标真实轨迹,因此依靠各传感器航迹间相对位置信息进行航迹关联判断的算法^[2,3]适用性大大降低 ...

2013

0.0

2006

0.0

2008

0.0

2011

0.0

2008

0.0

2009

0.0

2011

0.0

. 2011, 33(1):190-195 DOI:10.3969/j.issn.1001506X.2011.01.39

Fuzzy track alignment-correlation algorithm based on target invariable information

基于目标不变信息量的模糊航迹对准关联算法

Song Qiang , Xiong Wei , Ma Qiang.

宋强, 熊伟, 马强

1. Research Institute of Information Fusion, Naval Aeronautical and Astronautical University, Yantai 264001, China; 2. Educational Administration Department, Naval Aeronautical and Astronautical University, Yantai 264001, China

This paper researches the track correlation problem with measuring systematic errors in the radar network and analyzes that how do the systematic errors affect the detected tracks of targets theoretically, then expresses the effect caused by the systematic errors as some rotation and mass motion. So the relative topology relation between targets wouldn’t be affected by the systematic errors. On this basis, a fuzzy binary track alignment-correlation algorithm based on target topology is provided. The algorithm takes the target topology information into account synthetically and constructs the target topology fuzzy element set. Then the algorithm resolves the problem of target track alignment-correlation by using fuzzy information processing theory, and can correlate the target tracks with a good performance prior to registration.

探讨了在组网雷达存在系统误差情况时的目标航迹对准关联问题。通过将探测系统误差对目标航迹的影响表示为各目标航迹数据的旋转和平移，从而说明了目标之间的相对拓扑关系不受系统误差影响；由此提出了一种雷达组网模糊航迹对准关联算法，该算法通过提取包括目标间拓扑信息在内的各种不受系统误差影响的目标不变信息量，采用模糊信息处理理论来解决目标航迹的对准关联问题，从而较好地实现了误差配准前的准确航迹对准关联。

... ②以融合质心位置及航向建立参照系进行目标拓扑描述,比目标参照系^[9]的精度和稳定性更高 ...

2004

0.0

... ③利用航迹历史信息和灰色关联分析方法^[10],对各传感器航迹拓扑描述向量进行关联匹配 ...

2006

0.0

2013

0.0

... _ij(k)为统计量,L(k)为目标函数的二维分配模型^[12,13],求解全局最优的航迹关联关系: ...

2012

0.0

... _ij(k)为统计量,L(k)为目标函数的二维分配模型^[12,13],求解全局最优的航迹关联关系: ...

2010

0.0

. 2010, 32(4):898-901 DOI:10.3724/SP.J.1146.2009.00394

Track correlation algorithm based on multi-dimension assignment and grey theory

基于多维分配和灰色理论的航迹关联算法

Xiong Wei , Zhang Jing-wei , He You.

熊伟, 张晶炜, 何友

① The Fourth Research Academy of CASIC, Beijing 100854, China; ② Research Institute of Information Fusion, Naval Aeronautical Engineering Institute, Yantai 264001, China; ③ Department of Electronic Engineering, Tsinghua University, Beijing 100084, China

To resolve the problem of track correlation in distributed multi-sensor system, a track correlation algorithm based on multi-dimension assignment and gray theory is presented in this paper. Firstly, gray theory is applied to acquire a global statistical vector in the distributed multi-sensor system. Then, a multi-dimension gray similar degree matrix is build according to the global statistical vector. Based on this matrix, the track correlation results can be got by a multi-dimension assignment method. At last, the algorithm is compared with gray track correlation algorithm. The simulation results show that the performance of the algorithm here is much better than that of the gray track correlation algorithm in dense multi-target environments, more cross, split and maneuvering track situations. In this situations, its correct correlation rate is improved about 8.8 percent over that of the gray track correlation algorithm.

针对目前应用于分布式多传感器系统中航迹关联算法只能解决两局部节点航迹相关的问题，该文提出了一种基于多维分配的灰色航迹关联算法。该算法运用灰色理论获取各传感器航迹间的灰色关联度，以此关联度为多传感器系统的全局统计量构造多维灰色关联度矩阵，并根据此矩阵形成的多维分配问题的解获得各传感器航迹间的关联结果。仿真结果表明，在密集目标环境下和/或交叉、分岔及机动航迹较多的场合，该算法的性能明显优于传统方法，其正确关联率较灰色航迹关联算法提高了大约8.8%。

2012

0.0

... 环境2:平行编队目标是航迹关联算法研究中的另一种典型环境^[15],设目标数10,第一个目标初始位置为(130,120) km,相邻目标间隔300 m,初始速度为400 m/s,初始航向为30#cod#x000b0 ...