随着不同分辨率和尺寸比例显示设备不断普及, 相同分辨率图像在不同显示设备上可能会呈现不同畸变结果。为适应多样化的显示终端, 图像和视频的非等比例缩放成为亟待解决的关键问题。最简单有效的非等比例缩放方法是直接删除不重要的行和列, 但过度删除非重要区域会造成图像局部失真。传统图像缩放算法一般分为均匀缩放算法和图像剪切算法^{[1, 2, 3]}。其中均匀缩放算法在进行非等比例缩放时会造成图像主体拉伸或压扁; 整幅图像采用相同的缩放算子, 且不保留图像主体区域, 在分辨率较低时并不适用。而另一种广泛采用的图像缩放裁剪技术, 不可避免地导致图像信息的丢失。

近年来, 基于内容感知的缩放技术成为图像自适应缩放算法领域的研究热点。文献[4]提出一种基于鱼眼变形的图像缩放算法, 但该算法只能处理含有单个物体的图像。文献[5]利用图像分割划分区域, 在保护图像重要区域的同时却降低了系统的鲁棒性。目前最具代表性的内容感知缩放算法是线裁剪(Seam carving, SC)技术^[6], 该算法为获得不失真的非等比例缩放图像, 多次运用动态规划迭代, 使得计算量随图像分辨率而呈几何级数增长, 而且, 能量函数定义的局限也使得其存在结构失真的缺陷^[7]。在此基础上, 很多学者又提出多种改进算法^{[8, 9, 10]}。文献[11]提出基于重要度扩散和自适应采样的图像/视频缩放算法, 在重要区域的保护和整体概貌之间进行平衡, 避免过多删除非重要区域。但该算法在每删除一行和一列后都要对其相邻行或列进行重要度提升, 虽能得到较高的图像质量, 但仍存在计算量大的问题, 并不适用于实时的视频信号处理。

本文提出了一种基于随机置乱的内容感知图像缩放算法(Content-aware image resizing algorithm based on random permutation, CARP)。该算法将视觉显著图得到的行/列能量向量进行随机重排, 并按一定规则抽取原始图像中低于阈值的行/列。与SC算法相比, CARP算法在有效保护图像主体区域不发生畸变的同时, 能显著提高缩放速度, 是一种运算复杂度较低, 易于实时处理的内容感知缩放算法。

内容感知图像缩放结果对图像内容及重要性的定义有很高的依赖性, 比较理想的情况是选择一种符合人眼特性的图像重要度识别方法。文献[12]中提出的基于图形的视觉显著度模型(Graph-based visual saliency, GBVS)得到符合人眼特性98%的重要区域, 且该模型简单、合理。因此, 本文采用GBVS算法建立显著度图, 以提高图像内容识别精度。

1.1 单坐标方向尺寸缩放

单坐标方向尺寸缩放, 图像尺寸改变仅发生在水平或垂直单个方向。本文以列方向尺寸变换为例阐述算法内容。如果行方向尺寸变换, 仅需将图像进行转置处理即可。

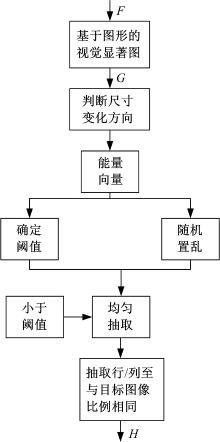
CARP算法如图1所示, 本文结合随机置乱能量向量的思想, 目的是在保护主体区域不被破坏的同时, 避免同一区域过度删除行或列, 从而达到非等比例缩放的目的。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 CARP算法在单坐标方向的原理框图Fig.1 Schematic diagram of CARP algorithm in single coordinate direction

假设输入原始图像F和待缩放目标图像H分辨率大小分别为m× n和m× n', 原始图像F进行单坐标方向尺寸变换, 即n-n'=c(c∈ z且c≠ 0)。当c> 0时, 通过本文算法删除列实现; 当c< 0时, 通过本文算法插入列实现。不失一般性, 以n-n'=c(c> 0)为例, 本文算法步骤如下:

步骤1 利用GBVS算法由原始图像F得到大小为m× n的显著图G。

步骤2 得到显著图G后, 需要计算能量向量。能量向量需要对显著图G的每一列进行求和得到, 令V=sum(G), 得到大小为1× n的能量向量V。

步骤3 将能量向量V随机置乱, 即使得置乱后向量内元素顺序随机排列, 令V_s=rand(V), 得到置乱后的向量V_s; 同时根据能量向量确定阈值T=1/2× max(V)。

步骤4 根据抽取列数c以及阈值T, 对置乱后的向量V_s进行均匀抽取, 假设置乱后向量V_s(i)(i≤ n, i∈ z⁺)满足V_s(i)< T, 则抽取; 否则, 寻找下一个满足条件的位置。

步骤5 如果步骤4结束后实际抽取列数c'< c, 即有剩余列未抽取, 返回步骤4继续执行, 直至c'=c, 结束。

经CARP算法计算后, 得到目标图像H, H即为非等比例缩放后的结果。

为了测试本文算法性能, 与文献[6]的SC算法进行比较, 其中GBVS的算法见文献[15]。在图2中, 给出3幅测试图像, 包括代表性的风景图、人物图和动物图。对3幅测试图像进行两组仿真实验, 表1给出缩放前后图像的分辨率, 第一组仿真实验中原始图像沿水平方向抽取20列, 第二组仿真实验中原始图像沿垂直方向抽取60行。表2显示SC算法和本文算法在二组仿真实验中的平均运行时间, 本文采用平均运行时间作为算法复杂度的评价指标。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 测试图像及分辨率Fig.2 Text images and resolution

表1

Table 1

表1(Table 1)

表1 分辨率改变 Table 1 Resolution changing 原始尺寸 缩放后尺寸 第一组 第二组 (a)480× 640 480× 620 420× 640 (b)402× 536 402× 516 342× 536 (c)480× 720 480× 700 420× 720

表1 分辨率改变 Table 1 Resolution changing

表2中两组仿真实验数据分析显示, 本文算法运算速度明显高于SC算法, 并且当缩放尺度较大时, SC算法运算速度明显降低, 而本文算法运算速度变化不明显。图3给出两种算法在图像缩小上的比较, 本文采用主观评价方法对缩放后

表2

Table 2

表2(Table 2)

表2 两组仿真实验平均运行时间 Table 2 Average run time of two groups simulation 计算时间/s 风景 人物 动物 第一组 SC算法 50.68 29.05 51.17 本文算法 3.18 2.86 3.04 第二组 SC算法 143.29 76.48 148.13 本文算法 3.24 2.97 3.07

表2 两组仿真实验平均运行时间 Table 2 Average run time of two groups simulation

图3

Fig.3

	Figure Option ViewDownloadNew Window
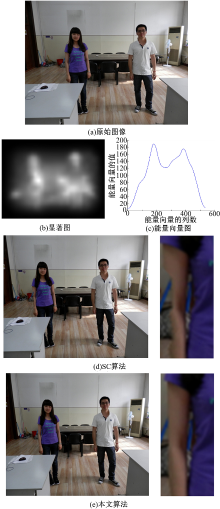	图3 第一组仿真在人物图上主观视觉效果的比较Fig.3 Subjective visual effect comparison in character of the first group simulation

图像质量进行评价。仿真实验结果表明, 本文算法在保护图像重要内容的同时, 获得了较好整体视觉效果, 避免了图像局部严重失真的现象。在图3(d)中, SC算法得到的图片出现明显局部失真现象, 图3(e)中, 用本文算法处理得到的图像主体区域没有失真现象发生, 且获得了较好的整体视觉效果。由于非等比例抽取方式的局限性, 本文算法在单方向抽取行/列数目存在极限, 该极限L为原始图像列/行与视觉主体宽/高之差, 抽取行/列数目越接近L, 得到的图像质量效果越差。如图4所示, 当抽取数目接近极限L时, 主体区域被抽取, 使得主体区域被破坏。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 图像行/列抽取数目接近极限L时的效果图Fig.4 Extraction number of row/column closing to limit

本文提出了CARP算法, 引入随机重排视觉显著图能量向量的思想, 在保护重要区域的同时, 避免在同一区域过度删除, 使得缩放后图像效果较好。与SC算法相比, 缩放尺度越大, CARP算法平均运行时间降低幅度越明显; 与直接删除行/列算法相比, 能够提高图像质量, 避免局部失真严重的问题。CARP算法在获得较好图像质量的同时, 大大降低了运算复杂度, 符合非等比例实时缩放的要求, 为今后在硬件平台上的实现提供了理论依据。