基于信号子空间的激光主动成像散斑去除

引用本文

王灿进, 孙涛, 王挺峰, 郭劲, 刘玉龙. 基于信号子空间的激光主动成像散斑去除. 2015, 45(4): 1347-1352
WANG Can-jin, SUN Tao, WANG Ting-feng, GUO Jin, LIU Yu-long. Speckle noise suppression method for laser active imaging based on signal subspace. Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1347-1352 复制到剪切板

Permissions

基于信号子空间的激光主动成像散斑去除

王灿进¹, 孙涛¹, 王挺峰¹, 郭劲¹, 刘玉龙²

1.中国科学院长春光学精密机械与物理研究所激光与物质相互作用国家重点实验室,长春 130033

2.吉林省烟草专卖局信息中心,长春130033

作者简介:王灿进(1987-),男,助理研究员,博士.研究方向:激光主动成像.E-mail:wcjpsh@126.com

基金:吉林省科技发展计划项目(20126015)

摘要

为研究激光主动成像中散斑噪声的抑制问题,提出一种基于信号子空间TDC(Time-domain constrained)的散斑去噪方法,并搭建一套基于距离选通ICCD的激光主动照明系统进行实验验证。首先使用同态变换将乘性噪声变为加性噪声,然后利用小波变换估计噪声的协方差;接着对含噪图像进行奇异值分解并估计信号子空间的维数,根据该维数对无噪图像的协方差矩阵进行特征值分解,计算出滤波估计矩阵。将滤波估计矩阵与含噪图像卷积,最后做同态逆变换,得到降噪后的图像。结果证明本文的去噪方法拥有比经典的Lee、Frost和Kuan算法更好的散斑噪声抑制效果,同时计算时间明显缩短。

关键词: 信息处理技术; 激光主动成像; 信号子空间; 散斑噪声; 时域限制; 同态变换

中图分类号:TN249 文献标志码:A 文章编号:1671-5497(2015)04-1347-06

Speckle noise suppression method for laser active imaging based on signal subspace

WANG Can-jin¹, SUN Tao¹, WANG Ting-feng¹, GUO Jin¹, LIU Yu-long²

1.State Key Laboratory of Laser Interaction with Matter, Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Science, Changchun 130033, China

2.Jilin Tobacco Monopoly Bureau Information Center, Changchun 130033, China

Abstract

To investigate the suppression of the speckle noise in laser active imaging, a denoising method based on Time-Domain Constrained (TDC) in signal subspace is proposed and a laser active imaging system based on range-gating ICCD is constructed for experiment. First, homomorphic transformation is performed to convert the multiplicative noise to additive noise. Second, wavelet transformation is performed to estimate the covariance of speckle noise. Third, the noise image is decomposed into signal subspace and noisy subspace, and singular value decomposing is used to estimate the dimension of the signal subspace. The covariance of clean image is decomposed using eigenvalue decomposing, and denoising estimating matrix is computed. Fourth, the denoising estimating matrix is convolved with noisy image. Finally, the inverse homomorphic transform is carried out to get the denoised image. Experiment results indicate that, compared with classical Lee, Frost and Kuan filtering, the proposed method has advanced denoising performance and consts less computation time.

Keyword: information processing; laser active imaging; signal subspace; speckle noise; TDC; homomorphic transformation

Show Figures

0 引言

激光主动成像^[1]系统具有分辨率高、抗干扰能力强、不受环境光限制等优点, 适用于微光、夜视以及远距离暗目标的探测成像, 目前已广泛应用于远距离监视、自动目标识别等领域^{[2, 3]}。在主动成像过程中, 由于相干光经过目标表面反射或者通过无规则涨落的折射媒介传播, 会形成一种信号相关的乘性噪声, 即散斑噪声, 造成图像质量严重下降。文献[4]通过计算灰度概率分布曲线证明散斑噪声是激光主动成像的主要噪声, 因此研究抑制散斑噪声的算法是大多数激光主动成像系统都必须考虑的内容。

国内外学者提出诸多抑制散斑噪声的经典算法, 包括均值滤波^[5]、Lee滤波^[6]、Frost滤波^[7]、Kuan滤波^[8]及其改进算法^[9]。这些滤波器使用一定大小的滤波窗口在图像上滑动, 使用不同算法计算出当前像素的替代值, 其中Lee滤波由于在滤除噪声和保留信号完整性之间能够达到较好的平衡而倍受关注。这类窗口算法虽然在同类区域去除散斑噪声效果较好, 但运算时间较长, 对于图像边缘和细节信息的保留能力也不理想。变换域降噪算法中使用较多的是小波软阈值滤波^{[10, 11]}, 这类算法缺陷在于阈值的选取较为困难, 阈值过大容易丢失图像细节信息, 阈值过小则不能很好地去除噪声。近年来出现了不少针对散斑噪声的新算法, 如Jarabo-Amores等^[12]提出一种基于“ mean-shift” 滤波的去噪方法, 该方法不必事先假设噪声的统计模型而能够达到与统计去噪相当的效果。Hyenkyun等^[13]提出基于交互技术(Shifting technology)的降噪方法, 能够快速有效地去除散斑噪声。国内, 文献[14]使用SURE(Stein's unbiased risk estimate)获得近似最优的小波系数的权值, 该方法优势在于计算量很小。

信号子空间方法的基本思想是将原始信号通过K-L变换分解为信号子空间和噪声子空间, 通过滤除噪声子空间噪声分量的同时保留信号子空间的信号部分, 能够恢复出较为纯净的信号, 该方法已经成功运用于语音和雷达信号降噪领域^{[15, 16]}。基于其优异的信噪分离效果, 本文将该方法从一维推广到二维空间, 提出一种基于时域约束(TDC)的激光主动成像散斑降噪方法。将本文的TDC降噪方法同经典的Lee、Frost和Kuan滤波作比较, 结果表明本文算法具有出色的噪声抑制效果, 同时算法也具有很好的实时性。

1 散斑噪声分析

被激光照射的目标表面相对于激光波长而言凹凸不平, 相干光被不同位置反射后在像面处发生干涉, 即形成散斑图样。散斑噪声的数学模型如式(1)(2)所示:

$\begin{matrix} \begin{matrix} I = I_{0} \cdot I_{sn} (1) \\ p (I_{sn}) = \frac{L^{L} I_{sn}^{L - 1}}{Γ (L)} e^{- L I_{sn}} (2) \end{matrix} \end{matrix}$

式中:I表示含噪图像; I₀表示无噪图像; I_sn表示散斑噪声作用系数, 服从均值为1, 方差为1/L的伽马分布, L是常数。

由式(1)可以看出散斑噪声是一种乘性噪声。为了将信号和噪声分离, 使用同态变换将其变为加性噪声:

$\begin{matrix} logI = \log I_{0} + \log I_{sn} (3) \end{matrix}$

记上式为:

$\begin{matrix} Y_{l} = X_{l} + N_{l} (4) \end{matrix}$

根据文献[17], 同态变换后散斑噪声的均值和方差的关系分别如式(5)(6)所示:

$\begin{matrix} \begin{matrix} E (N_{l}) = ψ (0, L) - \ln (L) (5) \\ var (N_{l}) = ψ (1, L) (6) \\ ψ (i, z) = {(\frac{d}{dz})}^{i} ψ (z) = {(\frac{d}{dz})}^{i + 1} lnΓ (z) (7) \end{matrix} \end{matrix}$

2 信号子空间滤波及TDC滤波方法

2.1 信号子空间

信号子空间技术是一种类似于傅里叶变换^[18]、小波变换^[19]的子空间变换技术。其原理是:带噪信号的空间由信号子空间与噪声子空间构成, 噪声能量均匀分布于整个空间中, 而信号能量则只分布于信号子空间中。将带噪信号分解至信号子空间和噪声子空间, 通过消去噪声子空间的分量, 就可以恢复出近似纯净的信号。该方法对于语音信号具有良好的去相关性, 因而广泛用于语音增强领域。本文接下来将这种方法推广到二维图像空间。

设无噪图像的估计为:

$\begin{matrix} {\hat{X}}_{(m \times n)} = H_{(m \times m)} Y_{(m \times n)} (8) \end{matrix}$

则误差信号表示为:

$\begin{matrix} ε = \hat{X} - X = (H - I) X + HN = ε_{x} + ε_{n} (9) \end{matrix}$

定义失真信号能量和残余噪声能量分别为:

$\begin{matrix} \begin{matrix} \overline{ε_{x}^{2}} = E (ε_{x} {ε^{T}}_{x}) = tr (E (ε_{x} {ε^{T}}_{x})) (10) \\ \overline{ε_{n}^{2}} = E (ε_{n} {ε^{T}}_{n}) = tr (E (ε_{n} {ε^{T}}_{n})) (11) \end{matrix} \end{matrix}$

式中:tr( )表示取对角线上的元素。

为使失真信号能量达到最小, 设置约束条件为:

$\begin{matrix} \underset{H}{\min \overline{ε_{x}^{2}}} 且 \frac{1}{m} \overline{ε_{n}^{2}} \leq σ^{2} (12) \end{matrix}$

式中:σ ²是常数。对上述约束最小值问题, 可以采用Kuhn-Tucker条件得到Lagrange多项式:

$\begin{matrix} L (H, μ) = \overline{ε_{x}^{2}} + μ (\overline{ε_{n}^{2}} - m σ^{2}) (13) \end{matrix}$

根据条件

$\begin{matrix} \{\begin{matrix} \nabla_{H} L (H, μ) = 0 \\ μ (\overline{ε_{n}^{2}} - m σ^{2}) = 0 \end{matrix} (14) \end{matrix}$

可以计算出滤波矩阵H的估计值:

$\begin{matrix} H_{TDC} = R_{X} (R_{X} + μ R_{N})^{- 1} (15) \end{matrix}$

式中:R_X=E(XX^T)是无噪图像的协方差矩阵, R_N=E(NN^T)是噪声的协方差矩阵, μ 是Lagrange算子。将R_X进行特征值分解, 表示成信号子空间和噪声子空间两部分:

$\begin{matrix} R_{X} = U Λ_{X} U^{T} = (\begin{matrix} U_{1} & U_{2} \end{matrix}) (\begin{matrix} Λ_{X_{1}} & 0 \\ 0 & Λ_{X_{2}} \end{matrix}) (\begin{matrix} {U^{T}}_{1} \\ {U^{T}}_{2} \end{matrix}) (16) \end{matrix}$

式中:U₁、U₂分别是m× r和m× (n-r)的特征值矩阵, r是信号子空间的维数, n-r是噪声子空间的维数; $\begin{matrix} Λ_{X_{1}} \end{matrix}$ 、 $\begin{matrix} Λ_{X_{2}} \end{matrix}$ 是特征值对角阵; U₁、 $\begin{matrix} Λ_{X_{1}} \end{matrix}$ 、 $\begin{matrix} {U^{T}}_{1} \end{matrix}$ 代表的是R_X在信号子空间的分量; U₂、 $\begin{matrix} Λ_{X_{2}} \end{matrix}$ 、 $\begin{matrix} {U^{T}}_{2} \end{matrix}$ 代表的是R_X在噪声子空间的分量。

取R_X的信号子空间的分量代入式(15), 可得滤波估计矩阵:

$\begin{matrix} H_{TDC} = U_{1} Λ_{X_{1}} (Λ_{X_{1}} + μ R_{N})^{- 1} {U^{T}}_{1} (17) \end{matrix}$

由式(16)(17)可知, 为了得到H_TDC, 需要确定以下四个参数:信号子空间的维数r、无噪图像的协方差矩阵R_X、噪声的协方差矩阵R_N以及常数μ 。

2.2 确定信号子空间维数r

估计信号子空间的维数, 可以用奇异值分解实现。信号Y的奇异值分解表示如下:

$\begin{matrix} Y = U_{m \times m} S_{m \times m} V_{m \times n} (18) \end{matrix}$

式中:S是Y的奇异值矩阵, S_{m× m}=diag(s₁, s₂, …, s_m), s₁≥ s₂≥ …≥ s_m, 即对角阵上的值采用降序排列。

信号某维度的奇异值大小代表该维度的重要程度, 奇异值越大, 对应该维度越重要。取S的前r个分量, 则Y可以近似表示为:

$\begin{matrix} Y \approx U_{m \times r} S_{r \times r} V_{r \times n} (19) \end{matrix}$

文中选取r的条件为:

$\begin{matrix} \overset{r}{\sum_{i = 1}} s_{i}^{2} / \overset{m}{\sum_{i = 1}} s_{i}^{2} \geq T_{r} (20) \end{matrix}$

式中:T_r是一个接近于1的阈值, 具体大小由实验决定。

由于像素值为0的像素点经过log变换会出现无穷小, 使Y无法进行奇异值分解, 因此同态变换前先将每个像素亮度增加10, 待取指数恢复之后再减去10。

2.3 确定无噪图像的协方差矩阵R_X、噪声的协方差矩阵R_N

经过同态变换之后乘性噪声变为加性噪声, 如式(4)所示, 则可以得到

$\begin{matrix} R_{X} = R_{Y} - R_{N} (21) \end{matrix}$

式中:R_Y=E(YY^T)可以直接由含噪图像求得。对于R_N, 式(6)给出了它和常数L的关系, 但是L难以估计。本文从小波分析的角度出发:在小波域上, 图像信号集中在低频分量, 而噪声信号均匀分布在整个小波空间^[16], 因此可以利用高频子带的小波系数估计噪声的强度:

R_N=k· ( $\begin{matrix} median (W_{1}^{HH} \end{matrix}$ )/0.6745)· I(22)

式中: $\begin{matrix} W_{1}^{HH} \end{matrix}$ 为含噪图像在高频子带的小波系数, median表示求中值, I为单位阵, k为一常数因子。加入调节因子k是因为经过同态变换之后方差会出现不可预计的偏差, 通过调整k的值使噪声方差取值合理, 实验中k∈ (0, 100)。

2.4 确定常数μ

μ 的取值会影响滤波后图像的质量。μ 值大, 可以较大程度地滤除散斑噪声, 却会导致较严重的信号失真; μ 值小, 能够保留较多的细节信号, 但会残余更多的噪声。选择μ 的值需要在信号完整性和滤波性能之间权衡。

根据文献[16], 采用以下公式确定μ :

$\begin{matrix} μ = \{\begin{matrix} μ_{0} - SNR / s \\ 4 \\ 9 \end{matrix} \begin{matrix} , 5 < SNR (dB) < 20 \\ SNR (dB) \geq 20 \\ SNR (dB) \leq 5 \end{matrix} (23) \end{matrix}$

式中:SNR是图像的信噪比; μ ₀和s是常数, 由实验确定。

式(23)表示的是:对于高信噪比的图像, 噪声较小, μ 取较小的值, 以保护信号完整性为主要目标; 对于低信噪比的图像, 噪声较大, μ 取较大的值, 以滤波为主要目标。

2.5 基于信号子空间的TDC滤波方法

本文基于信号子空间的散斑去噪方法如下:

(1)对增加亮度后的图像进行同态变换, 将乘性噪声变为加性噪声。

(2)将图像进行小波变换, 并利用高频分量估计噪声方差R_N。

(3)对Y进行奇异值分解, 估计信号子空间的维数r。

(4)计算无噪图像的协方差矩阵R_X=R_Y-R_N, 并根据式(16)对其进行特征值分解。

(5)根据式(17)计算变换矩阵H_TDC, 得到无噪图像的估计值 $\begin{matrix} \hat{X} \end{matrix}$ =H_TDCY。

(6)同态逆变换, 得到最终的去噪图像。

3 实验验证

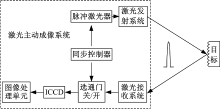
实验搭建一套基于距离选通技术的激光主动照明系统:使用532 nm波长、5 mrad发散角的半导体泵浦固体脉冲激光器发射脉冲光束照射3.4 km处的目标, 用选通ICCD接收反射信号, 通过同步控制器控制选通快门的开闭。其中选通ICCD由选通像增强器和CCD组成, 具有高增益、高灵敏度、成像清晰等优点。同步控制器控制ICCD在纳秒级的时间内进行选通, 可以抑制杂散光, 保证采集到较为清晰的含散斑图像。图1是实验系统框图, 图2是实验系统实物图。

	Figure Option View Download New Window
	图1 实验系统框图Fig.1 Block diagram of experimental system

	Figure Option View Download New Window
	图2 实验系统实物图Fig.2 Photo of experimental system

截取ICCD输出图像中被照亮的区域, 最终得到的实验图像大小为150× 150像素。分别采用Lee、Frost、Kuan和本文的TDC滤波方法进行实验, Lee、Frost和Kuan的滤波窗口均选为5× 5。窗口大小选为5× 5可以在滤除噪声和保留图像细节之间得到较好的平衡。实验编程环境为:Windows XP、i7-2600 3.40 GHz CPU、2G内存、VS2008+opencv软件平台。

图3为4种算法的滤波效果对比, ICCD的积分时间为50 ns。

	Figure Option View Download New Window
	图3 不同滤波方法的滤波结果Fig.3 Results of different denoising methods

从图3直观上看, Lee、Frost和Kuan结果图中残余较多的散斑噪声, 而TDC滤波后的图像最清晰, 滤波效果最好。观察图像下方中间的门框, 可以发现TDC滤波后的边缘更加清晰, 这是因为其余3种算法均使用邻域像素进行加权操作, 必将导致细节模糊。而TDC算法将图像矩阵当做整体进行运算, 是对图像信号的稀疏表示, 信号子空间的信号部分没有损失, 故边缘保持能力更强。

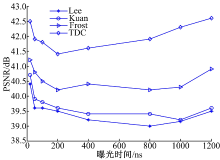
本文引入峰值信噪比PSNR^[20]以评价滤波算法的有效性。改变ICCD的积分时间, 得到不同噪声强度的图像, 分别用4种滤波方法进行实验, 计算其PSNR值, 比较滤波效果, 结果如图4所示。

	Figure Option View Download New Window
	图4 不同滤波算法的PSNR曲线Fig.4 PSNR curves of different denoising methods

由图4看出, 本文TDC算法对于不同强度的噪声能够取得比经典的Lee、Frost和Kuan算法更好的滤除效果。观察PSNR曲线, 随着曝光时间的增加, TDC滤波算法的曲线与其余曲线的差值越来越大, 这表示随着噪声的增大, TDC的滤波性能优势相对于其余算法越来越突出。这是因为对于Lee、Frost和Kuan等窗口滤波而言, 使用有限大小的滤波窗口信息, 并不能很好地估计噪声的方差, 随着噪声的增加, 滤波能力并不会显著提升, 滤波后残余的噪声会越来越大。而TDC算法的约束条件是将残余噪声限制在σ ²范围内, 算法在整个图像上进行噪声强度的估计, 并且只保留信号子空间中的非常小的噪声能量, 因此滤波效果更好。

表1统计的是不同算法对于150× 150图像的平均运算时间。可见本文算法比其余3种算法耗时要小得多。这是因为TDC算法对整个图像矩阵同时进行计算, 而其余3种算法均需要滑动滤波窗口遍历整个图像区域。在本文的实验条件下(成像区域大小为150× 150, 帧频为25 帧/s), TDC滤波算法能够满足实时处理的要求。

表1 不同算法的平均运算时间 Table 1 Average running time of different denoising methods

4 结束语

受语音增强领域的子空间分解方法的启发, 本文在分析散斑噪声数学模型的基础上, 提出一种基于信号子空间的激光主动成像去噪方法, 并搭建了一套基于距离选通技术的激光主动照明系统进行实验验证。本文算法将含噪图像分解为信号子空间和噪声子空间, 通过去除噪声子空间并尽量保留信号子空间的能量, 以取得良好的去噪效果。结果证明本文TDC方法具有比经典的Lee、Frost和Kuan算法更好的去噪性能, 同时缩短了计算时间, 满足激光主动成像系统实时性的要求。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	王灿进, 孙涛, 石宁宁, 等. 基于双隐含层BP算法的激光主动成像识别系统[J]. 光学精密工程, 2014, 22(6): 1639-1647. Wang Can-jin, Sun Tao, Shi Ning-ning, et al. Laser active imaging and recognition system based on double hidden layer BP algorithm[J]. Opt Precision Eng, 2014, 22(6): 1639-1647. [本文引用:1]
[2]	钱方, 孙涛, 郭劲, 等. 无参考的特征点复杂度激光干扰图像评估[J]. 光学精密工程, 2015, 23(4): 1179-1186. Qian Fang, Sun Tao, Guo Jin, et al. No-reference laser-dazzling image quality assessment based on feature-point complexity[J]. Opt Precision Eng, 2015, 23(4): 1179-1186. [本文引用:1]
[3]	赵建川, 王弟男, 陈长青, 等. 红外激光主动成像和识别[J]. 中国光学, 2013, 6(5): 795-802. Zhao Jian-chuan, Wang Di-nan, Chen Chang-qing, et al. Infrared laser active imaging and recognition technology[J]. Chinese Optics, 2013, 6(5): 795-802. [本文引用:1]
[4]	李自勤, 李琦, 王骐. 由统计特性分析激光主动成像系统图像的噪声性质[J]. 中国激光, 2004, 31(9): 1081-1085. Li Zi-qin, Li Qi, Wang Qi. Noise characteristic in active laser imaging system by statistic analysis[J]. Chinese Journal of Lasers, 2004, 31(9): 1081-1085. [本文引用:1]
[5]	Loupas T, McDicken W, Allan P. An adaptive weighted median filter for speckle suppression in medical ultrasonic images[J]. IEEE Trans Circuits System, 1989, 36(1): 129-135. [本文引用:1]
[6]	Lee J S. Digital image enhancement and noise filtering by use of local statistics[J]. IEEE Trans Pattern Analysis and Machine Intell, 1980, 20: 165-168. [本文引用:1]
[7]	Frost V S, Stiles J A, Shanmugan K S, et al. A mode for radar images and its application to adaptive digital filtering of multiplicative noise[J]. IEEE Trans Pattern Analysis and Machine Intell, 1982, 4: 157-165. [本文引用:1]
[8]	Kuan D, Sawchuk A, Strand T, et al. Adaptive restoration of images with speckle[J]. IEEE Trans Acoust, Speech and Signal Process, 1987, 35(3) : 373-383. [本文引用:1]
[9]	Lu Y H, Tan S Y, Yeo T S, et al. Adaptive filtering algorithms for SAR speckle reduction[C]∥Geoscience and Remote Sensing Symposium, Lincoln, NE, USA, 1996. [本文引用:1]
[10]	Donoho D L. Denoising by soft-thresholding[J]. IEEE TransInform Theory, 1995, 41(3): 613-627. [本文引用:1]
[11]	叶树亮, 张玉德, 张炜. 齿轮视觉检测中的尺度与方向相关性联合降噪[J]. 光学精密工程, 2014, 22(6): 1622-1630. Ye Shu-liang, Zhang Yu-de, Zhang Wei. Scale and directional correlation combined denoiseing in gear visual inspection[J]. Opt Precision Eng, 2014, 22(6): 1622-1630. [本文引用:1]
[12]	Jarabo-Amores P, Rosa-Zurera M, Mata-Moya D, et al. Mean-shift filtering to reduce speckle noise in SAR images[C]∥Instrumentation and Measurement Technology Conference, Singapore, 2009. [本文引用:1]
[13]	Hyenkyun W, Yun S. Alternating minimization algorithm for speckle reduction with a shifting technique[J] . Image Processing, 2012, 21(4): 1701-1714. [本文引用:1]
[14]	李晓峰, 徐军, 罗积军, 等. 激光主动成像图像噪声分析与抑制[J]. 红外与激光工程, 2011, 40(2): 332-337. Li Xiao-feng, Xu Jun, Luo Ji-jun, et al. Noise analyzing and denoising of intensity image for laser active imaging system[J]. Infrared and Laser Engineering, 2011, 40(2): 332-337. [本文引用:1]
[15]	Ikeda S, Ohtsuki T, Tsuji H. Signal-subspace-partition event filtering for eigenvector-based security system using radio waves[C]∥Personal, Indoor and Mobile Radio Communications, Tokyo, Japan, 2009. [本文引用:1]
[16]	Gu J, Yang J, Zhang H, et al. Speckle filtering in polarimetric SAR data based on the subspace decomposition[J]. Geoscience and Remote Sensing, 2004, 42(8): 1635-1641. [本文引用:2]
[17]	Donoho D L, Johnstone I M. Ideal spatial adaptation by wavelet shrinkage[J]. Biometrika, 1994, 81(3): 425-455. [本文引用:1]
[18]	邓建青, 刘晶红. 基于Fourier-Mellin变换和Keren算法的改进运动估计算法[J]. 液晶与显示, 2011, 26(3): 364-369. Deng Jian-qing, Liu Jing-hong. Improved motion estimation algorithm based on Fourier-Mellin transform and Keren algorithm[J]. Chinese Journal of Liquid Crystals and Displays, 2011, 26(3): 364-369. [本文引用:1]
[19]	任志英, 高诚辉, 申丁, 等. 双树复小波稳健滤波在工程表面粗糙度评定中的应用[J]. 光学精密工程, 2014, 22(7): 1820-1827. Ren Zhi-ying, Gao Cheng-hui, Shen Ding, et al. Application of DT-CWT robust filtering to evaluation of engineering surface roughness[J]. Opt Precision Eng, 2014, 22(7): 1820-1827. [本文引用:1]
[20]	任文琦, 王元全. 基于梯度矢量卷积场的四阶各向异性扩散及图像去噪[J]. 光学精密工程, 2013, 21(10): 2713-2719. Ren Wen-qi, Wang Yuan-quan. GVC-based fourth-order anisotropic diffusion for image denoising[J]. Opt Precision Eng, 2013, 21(10): 2713-2719. [本文引用:1]

2014

0.0

... 0 引言激光主动成像^[1]系统具有分辨率高、抗干扰能力强、不受环境光限制等优点,适用于微光、夜视以及远距离暗目标的探测成像,目前已广泛应用于远距离监视、自动目标识别等领域^[2,3] ...

2015

0.0

2013

0.0

. 2013, 6(5):795-802 DOI:10.3788/CO.20130605.0795

Infrared laser active imaging and recognition technology

红外激光主动成像和识别

Zhao Jian-chuan , Wang Di-nan , Chen Chang-qing

赵建川, 王弟男, 陈长青

1. Aviation Commissary of Navy in Changchun, Changchun 130033, China; 2. State Key Laboratory of Laser Interaction with Matter, Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China

An experiment platform for laser active imaging and target recognition was built combining a laser active image system and the target recognition technology, and the target recognition after laser active imaging was mainly researched. The feature vector was comprised of seven invariant Hu moments. The BP neural network algorithm comprised of 136 weight coefficients was used to study the moving target, a 43 submachine gun model at 450 m from the experiment platform at night, and excellent experiment results were obtained. It shows clear imaging effects by 68.87% of target recognition statistic probability in 2 740 frames of laser active imaging, and the probability of rotation transformation reaches 80.05%. These researches are significant to the detection and recognition of little targets at night.

在传统激光主动成像系统的基础上,结合目标识别技术搭建了一台激光主动成像识别系统实验平台,研究了激光主动成像后的目标识别技术。由7个不变Hu矩构成特征量,用由136个权值系数构成BP神经网络算法对黑夜条件下450 m处的运动目标—43式冲锋模具枪进行了实验研究。研究显示,采用该方法成功获得了清晰的红外激光主动成像效果,对2 740 frame激光主动成像图像的统计目标识别率达到了68.87%,其中旋转变换下的统计识别率可达80.05%。该项研究对实际黑夜暗小目标的探测识别具有重要意义。

2004

0.0

1989

0.0