基于MSA特征和模拟退火优化的遥感图像多目标关联算法

引用本文

李晖晖, 滑立, 杨宁, 刘坤. 基于MSA特征和模拟退火优化的遥感图像多目标关联算法. 2015, 45(4): 1353-1359
LI Hui-hui, HUA Li, YANG Ning, LIU Kun. Multi-target association algorithm for remote sensing images based on MSA features and simulated annealing optimization. Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1353-1359 复制到剪切板

Permissions

基于MSA特征和模拟退火优化的遥感图像多目标关联算法

李晖晖¹, 滑立¹, 杨宁¹, 刘坤²

1.西北工业大学自动化学院,西安 710072

2.上海海事大学信息工程学院,上海 200135

作者简介:李晖晖(1974-),女,副教授,博士.研究方向:数字图像处理,图像信息融合.E-mail:lihhui@nwpu.edu.cn

基金:航空基金(20131953022); 西北工业大学基础研究基金项目(JC20110266); 装备研究基金项目(9140A06050113HK****)

摘要

由于当前遥感成像技术一般只能获取采样稀疏的遥感图像,无法准确估计目标的状态信息,因此传统的利用状态特征进行关联的方法并不适合遥感图像的目标关联。选取不依赖于时间的目标图像特征作为关联量又无法处理大场景中多个目标关联引起的模糊性。针对上述问题,本文提出了基于多尺度自卷积不变矩特征匹配和模拟退火优化的多目标关联算法。首先提取目标的多尺度自卷积矩(MSA)特征,计算特征间匹配概率,构造整体关联代价矩阵,并设置自适应温度更新函数和双阈值对模拟退火算法进行改进,快速寻求全局最优解。实验结果表明,该算法能够有效地利用遥感图像特征信息,消除关联模糊性,高效解决多目标关联问题。

关键词: 摄影测量与遥感技术; 目标关联; MSA特征; 关联代价矩阵; 模拟退火算法

中图分类号:TP751 文献标志码:A 文章编号:1671-5497(2015)04-1353-07

Multi-target association algorithm for remote sensing images based on MSA features and simulated annealing optimization

LI Hui-hui¹, HUA Li¹, YANG Ning¹, LIU Kun²

1.College of Automation, Northwestern Polytechnical University, Xi'an 710072,China

2.School of Information Engineering, Shanghai Maritime University, Shanghai 200135, China

Abstract

Since the current remote sensing imaging techniques can only get sparse sampling remote images, which are unable to accurately estimate the target state information, so the traditional association method using state features is not suitable for remote sensing image target. If the time independent image features are selected as the associative volume, the ambiguity induced by the association multiple targets in big scene can not be handled. To solve the above problem, a multi-scale autoconvolution feature matching and simulated annealing optimization algorithm is proposed. First, the MSA features are extracted and the matching probability between features is calculated to construct the whole association cost matrix. Then, the adaptive temperature updating function and the double threshold are set to improve the simulated annealing algorithm for quick search of the global optimal solution. Experimental results show that the proposed algorithm can effectively use the feature information of remote sensing image, eliminate association ambiguity and solve the problem of multi-target association efficiently.

Keyword: photogrammetry and remote sensing; target association; msa feature; association cost matrix; simulated annealing algorithm

Show Figures

0 引言

多源遥感图像融合^[1]能够综合利用多源互补的图像信息以提高信息的准确性与可靠性, 因此在诸多领域得到广泛应用, 包括军事、测绘、地质、农业及灾情监测等。而目标关联是融合的先决条件, 概括来说就是在两幅(或多幅)不同时间(或空间)获取的遥感图像中, 将来自同一目标的信息进行匹配。然后才能进行融合检测、识别、跟踪等一系列处理。

以往的目标关联方法主要指状态滤波类方法, 将目标视为点对象, 利用雷达型数据提供的目标位置、速度、方位等运动特征进行关联, 适合密集采样的序列图像。如文献[2]提出了基于目标质心及质心偏移量的联合概率数据关联(Joint probabilistic data association, JPDA)方法, 首先将目标与背景分割, 然后计算目标区域的质心, 以估计目标的运动信息, 最后利用JPDA方法^[3]实现关联与跟踪。文献[4]提出了在红外系统中将目标检测和跟踪联合设计的方法, 利用多假设跟踪(Multiple hypothesis tracking, MHT)算法进行目标图像特征点的匹配跟踪。但由于当前遥感成像技术一般只能获取采样稀疏的遥感图像, 很难预测目标的状态量, 因此信息融合领域中传统的利用状态特征进行关联的方法并不适合遥感图像的目标关联。需要利用目标图像自身特征进行匹配, 来建立新的目标关联准则。文献[5]结合Gabor小波提取特征以及迭代最小平方和的方法, 实现目标尺度变化、旋转及平移等几何变形时的跟踪。文献[6]首先提取目标图像的8个不变矩特征, 然后通过训练神经网络实现目标的匹配和定位。

首先需要解决图像特征的提取问题。不变矩方法是解决图像特征不变性的常用方法, 它能够克服视点变化对特征量的干扰, 最具代表性的就是Hu矩特征^[7]。2005年Rahtu等^[8]结合多尺度几何分析方法, 在Hu矩特征的基础上, 研究了可以同时捕获空间特性和图像强度的多维不变描述子, 构造了多尺度自卷积矩(Multi scale autoconvolution, MSA)特征, 实践证明这是目前最稳健的不变矩特征之一^[8]。然后采用距离度量法进行特征匹配, 但由于遥感信息的不确定性和特征提取算法的不精确性导致特征匹配结果存在误差, 因此需要进行关联修正来消除多目标对应关系的模糊性。文献[9]对上述问题提供了一种解决思路, 首先利用目标特征匹配结果构造一个多目标关联代价矩阵(Association cost matrix, ACM), 然后采用模拟退火算法求解使整体关联代价最小的关联代价矩阵, 即为最终多目标关联结果。

本文借鉴文献[9]的思想, 将基于MSA特征匹配和关联代价矩阵最优化的多目标关联算法应用于海地机场飞机多目标关联问题上, 在组合优化过程中, 着重对模拟退火算法进行了改进:在原始算法的搜索过程中设定内、外循环迭代次数, 并设计了一种新的温度更新函数, 它具有一定的自适应性, 改进了温度控制方式, 提高了搜索效率。通过海地机场6类飞机灰度图像进行多组实验, 结果证明了本文算法具有很好的多目标关联效果。

1 多尺度自卷积矩(MSA)

多尺度自卷积矩(MSA)是迄今为止最为有效的不变矩。MSA变换的基本原理:图像中任意一点的坐标可以用其他随机不共线三点的坐标线性表示, 对图像进行仿射变换时, 这四个点线性表示的系数不会发生变化, 因此可利用系数不变性质构造仿射不变量, 具有较好的稳定性。

定义图像的仿射变换为A=A(T, t), 设图像仿射变换前后的坐标分别为x和x', 即x'=A(x)=Tx+t。设f为图像的灰度函数, 仿射变换后的图像为f'(x')=f(Tx+t)。

设x₀, x₁, x₂∈ R²是f(x)定义域中的3个点, 则点μ _α_,_β可线性表示为:

$\begin{matrix} μ_{α, β} = α (x_{1} - x_{0}) + β (x_{2} - x_{0}) + x_{0} (1) \end{matrix}$

μ '_α_,_β可表示为:

$\begin{matrix} \begin{matrix} μ'_{α, β} = α (x'_{1} - x'_{0}) + β (x'_{2} - x'_{0}) + x'_{0} = \\ T μ_{α, β} + t (2) \end{matrix} \end{matrix}$

式中:x'₀, x'₁, x'₂分别对应于x₀, x₁, x₂的仿射变换。可见随机变量f(μ _α_,_β)和f'(μ '_α_,_β)有着相同的分布, 因此其数学期望也相等, 这种相等关系独立于仿射变换。MSA方法即为变量f(μ _α_,_β)的数学期望值:

$\begin{matrix} F (α, β) = E [f (u_{α, β})] = \overset{}{\int_{R^{2}}} f (u) p_{U_{α, β}} (u) du (3) \end{matrix}$

单纯从数学上考虑积分元素在积分域内的任意性, 可知F(α , β )就是仿射变换的不变特征。设γ =1-α -β , 则μ _α_,_β=α x₁+β x₂+γ x₀。概率密度函数 $\begin{matrix} p_{U_{α, β}} \end{matrix}$ (u)=(p_α× p_β× p_γ)(u), 可将式(3)改写为:

$\begin{matrix} \begin{matrix} F (α, β) = \overset{}{\int_{R^{2}}} f (u) p_{U_{α, β}} (u) du = \\ \overset{}{\int_{R^{2}}} f (u) (p_{α} \times p_{β} \times p_{γ}) (u) (4) \end{matrix} \end{matrix}$

为方便计算, 将式(4)转至频域, $\begin{matrix} \hat{f} \end{matrix}$ 是f的傅立叶变换, 得到:

$\begin{matrix} F (α, β) = \frac{1}{\hat{f} {(0)}^{3}} \overset{}{\int_{R^{2}}} \hat{f} (- ξ) \hat{f} (αξ) \hat{f} (βξ) \hat{f} (γξ) dξ (5) \end{matrix}$

2 关联代价矩阵(ACM)

2.1 构造ACM

研究两幅遥感图像中的目标关联问题, 可将其看作2维分配问题^[10]。假设前一图像中有M个目标Z¹={ $\begin{matrix} z_{m}^{1} \end{matrix}$ , m=0, 1, …, M}, 后一图像中有N个目标Z²={ $\begin{matrix} z_{n}^{2} \end{matrix}$ , n=0, 1, …, N}。现在定义一个二值分配变量:

$\begin{matrix} a (m, n) = \{\begin{matrix} 1, 目标 z_{m}^{1} 分配给目标 z_{n}^{2} \\ 0, 其他 \end{matrix} \end{matrix}$

于是可用此形成整体关联矩阵:a={a(m, n); m=0, 1, …, M; n=0, 1, …, N}, 关联的目的是找到最优关联矩阵 $\begin{matrix} \tilde{a} \end{matrix}$ 使得下面的全局关联代价最小:

$\begin{matrix} \begin{matrix} C (a) = \overset{M}{\sum_{m = 0}} \overset{N}{\sum_{n = 0}} a (m, n) c (m, n) \\ \tilde{a} = \arg \min_{a} C (a) (6) \end{matrix} \end{matrix}$

提取出各目标的MSA特征后, 通过计算目标特征之间的欧氏距离可获得任意两目标的MSA特征匹配代价, c $\begin{matrix} (m, n) \end{matrix}$ =‖ f_m_{, 1}-f_n_{, 2}‖ , m=0, 1, …, M; n=0, 1, …, N, 其中f_m_{, 1}为前一幅图像中目标m的k维MSA特征, f_n_{, 2}为后一幅图像中的k维MSA特征。C={a(m, n)c(m, n); (m=0, 1, …, M); (n=0, 1, …, N)}为关联代价矩阵。当m=n=0时, 表示两幅图像之间没有发生匹配, c(0, 0)可设为较大的正数。当m或n有一个为0时, 表示存在漏检或虚警等问题, 此时令c(m, n)≥ $\begin{matrix} \max_{m \neq 0, n \neq 0} \end{matrix}$ {c}。

由此可将遥感图像多目标关联问题转化为寻找关联矩阵 $\begin{matrix} \tilde{a} \end{matrix}$ , 使得全局关联代价矩阵C的能量最小。那么如何定量描述关联代价矩阵的能量最小状态是需要解决的问题, 必须根据具体应用来进行数学建模并优化。

2.2 ACM最优化

假设同一幅图像中目标种类各不相同, 根据多目标关联的具体应用, 优化建模需要满足如下条件:两幅图像最多只能分配给对方一个目标。数学表述即为“ 关联矩阵a中每一行和每一列只有一个值为1” , 以此构造可行的关联矩阵。设C={C₁, C₂, …, C_k}为所有可行的关联代价矩阵的集合, E(C_i)为对应于C_i的目标函数值。构造关联代价矩阵最优化的数学模型为:E(C^*)=minE(C_i), C^*∈ C, ∀ C_i∈ C。目标函数的最小值对应关联代价矩阵的最优解, 即关联代价矩阵的能量最小^[11]。为方便表述, 记a $\begin{matrix} (m, n) \end{matrix}$ 为a_mn, 考虑到实际的约束条件, 进一步将目标函数定义如下:

$\begin{matrix} \begin{matrix} E = \frac{A}{2} \overset{M}{\sum_{m = 1}} |\overset{N}{\sum_{n = 0}} a_{mn} - 1| + \frac{B}{2} \overset{N}{\sum_{n = 1}} |\overset{M}{\sum_{m = 0}} a_{mn} - 1| + \\ \overset{M}{\sum_{m = 0}} \overset{N}{\sum_{n = 0}} c_{mn} a_{mn} (7) \end{matrix} \end{matrix}$

式中:前两项为惩罚项, 对应具体的约束条件, 只有当前两项均为零时, 第三项才是多目标关联的实际代价。不考虑关联为空的情况, 设定A、B为较大的正数, 只有当关联矩阵a中每一行和每一列有且只有一个元素为1、其余元素均为零时, 求得的目标函数值才会最小, 对应的关联矩阵即为最优关联结果。

3 模拟退火算法

3.1 传统模拟退火算法

在实际优化问题中, 有些目标函数具有非凸性, 存在局部最优解, 尤其是当优化问题规模增大时, 迅速增加的局部最优解数目将会导致全局优化结果不够准确, 同时又增加了计算量。模拟退火算法^[12](Simulated annealing, SA)是基于Monte-Carlo迭代求解策略的一种随机寻优算法, 它来源于对固体退火过程的模拟, 挖掘物理工程中固体物质的退火降温过程与组合优化问题的相似性, 从理论上来说, 它是一种近似全局最优算法。1983年, Krickpatric等人将模拟退火算法成功应用于大规模组合优化问题的求解^[12]。

模拟退火过程大致分为以下三个阶段:

(1)升温阶段:加热时, 固体内部粒子随着温度的升高, 运动增强, 当温度足够高, 固体变为无序状, 内能增大。升温阶段对应算法的设定初始温度(充分大)。

(2)平衡阶段:退火过程中, 根据热力学定律可知在每一温度下, 系统自由能逐步减到最小时, 即达到平衡态。等温下热平衡过程可用Monte Carlo方法模拟, 为使结果精确, 需要大量采样, 导致计算量很大。为提高搜索效率, 1953年, Metropolis等人提出重要性采样法, 粒子在当前温度T趋于平衡态的概率为χ =exp(-Δ E/kT), 其中Δ E为内能改变量, k为Boltzmann常数。依据概率χ > r=random[0, 1]接受该状态为重要状态。上述接受新状态的准则称Metropolis准则^[13], 相对Monte Carlo方法来说, 计算量明显减少。

(3)冷却阶段:随着温度缓慢降低, 固体内部粒子运动渐趋有序, 同时能量下降。本阶段, 采用合适的温度衰减函数即退火策略来控制算法进程。最简单也最常用的控制参数衰减函数为:T_k=aT_k-₁=a^kT₀(k=1, 2, …), 其中, a是常值, 取0.5~0.9。重复执行新状态产生及判断是否接受新状态的过程, 逐渐降温直到趋于零时, 达到能量最小状态, 即求得全局最优解。

3.2 改进模拟退火算法寻优

模拟退火算法是一种启发式搜索方法, 它具有原理简单、适合求解组合优化问题中的全局(或近似)最优解^[14]、适用范围广等优点, 但也存在一些缺点:当变量过多、构造的目标函数较复杂时, 为获得较精确的全局最优解, 初始温度需要足够高且降温幅度要小, 这将导致迭代搜索过程缓慢, 求解时间太长, 工业应用较困难; 在Metropolis准则依概率接受新状态环节中, 有可能丢失当前最优解而陷入局部最优解邻域。

针对上述问题, 为确保算法的优化质量, 同时又提高算法的搜索效率(时间性能), 本文研究了以下改进算法:选择合适的初始温度和终止温度, 并设计高效的退火策略, 改进对温度的控制方式, 设计一个新的温度更新函数, 根据某一温度下状态被接受的次数来决定降温幅度, 保证温度更新有一定的自适应性。在搜索过程中设置双阈值, 即内、外循环的迭代次数, 若目标函数值在当前温度下保持s_max步不变, 记为当前最优解; 判断在T $\begin{matrix} (i + 1) \end{matrix}$ 温度下求得的关联矩阵 $\begin{matrix} \tilde{a} \end{matrix} \begin{matrix} (i + 1) \end{matrix}$ 与上一温度T $\begin{matrix} (i) \end{matrix}$ 下求得的关联矩阵 $\begin{matrix} \tilde{a} \end{matrix} \begin{matrix} (i) \end{matrix}$ 是否一致, 若外循环连续iter_max步降温过程中搜索到的最优关联矩阵均保持不变, 可认为得到了较高质量的全局最优解。具体步骤如下:

(1)给定初始温度T_max, 最终温度T_min;

(2)T $\begin{matrix} (0) \end{matrix}$ =T_max, i=1, 外循环迭代次数iter_num=1, 随机产生一个初始解a₀, 令 $\begin{matrix} \tilde{a} \end{matrix}$ =a₀, 并计算目标函数值E $\begin{matrix} (a_{0}) \end{matrix}$ ;

(3)Do while T $\begin{matrix} (i) \end{matrix}$ > =T_min;

a) fors_num=1~s_max;

b)根据约束条件, 产生一新解a_new, 计算新的目标函数值E $\begin{matrix} (a_{new}) \end{matrix}$ , 并计算目标函数值的增量Δ E=E $\begin{matrix} (a_{new}) \end{matrix}$ -E $\begin{matrix} (\tilde{a}) \end{matrix}$ ;

c)如果Δ E< 0, 则 $\begin{matrix} \tilde{a} \end{matrix}$ =a_new;

d)如果Δ E> 0, 则p=exp(-Δ E/T $\begin{matrix} (i) \end{matrix}$ );

如果p> R=random[0, 1], $\begin{matrix} \tilde{a} \end{matrix}$ =a_new; 否则 $\begin{matrix} \tilde{a} \end{matrix}$ = $\begin{matrix} \tilde{a} \end{matrix}$ , s_num=s_num+1;

e) End for

(4)退温β =s_num/(s_num+maxstep), $\begin{matrix} (i + 1) \end{matrix}$ =T $\begin{matrix} (i) \end{matrix}$ × e^-β, i=i+1; 如果局部最优关联矩阵 $\begin{matrix} \tilde{a} \end{matrix} \begin{matrix} (i + 1) \end{matrix}$ = $\begin{matrix} \tilde{a} \end{matrix} \begin{matrix} (i) \end{matrix}$ , 则iter_num=iter_num+1; 否则iter_num=1;

(5)如果iter_num> =iter_max, End Do, 否则返回(3);

(6)输出全局最优解, 计算结束。

4 实验结果及分析

为了检验所提方法的可行性, 选用如图1所示的海地机场6类飞机目标灰度图像进行实验(这些图像来自于某些海地机场的IKONOS卫星图像, 如图2所示, 它的分辨率为1 m, 大小为3000× 3000像素), 每幅图像大小为128× 128像素。考虑到实际图像会受到噪声干扰、遮挡、亮度变化等情况的影响, 我们除了对图像进行尺度缩放、旋转、仿射变换外, 还对图像加入了不同等级的高斯白噪声、遮挡以及亮度变化。构成了多组6类待关联的飞机目标, 下面给出了原始飞机目标和其中6组仿真图像, 如图3所示。

	Figure Option View Download New Window
	图1 海地机场6类飞机目标Fig.1 Six class aircraft targets of Haiti airport

	Figure Option View Download New Window
	图2 IKONOS卫星图像(海地机场)Fig.2 IKONOS satellite image(Haiti airport)

	Figure Option View Download New Window
	图3 6组仿真图像Fig.3 Six group simulation image

以图2中的飞机目标和图3中其仿真的待关联目标进行关联为例:首先在集合{-1, -0.75, -0.5, -0.25, 0, 0.25, 0.5, 0.75, 1}中取任意两元素的组合构成29对(α , β )值, 进而计算各飞机目标的29维MSA特征向量, 通过距离度量法获得两两匹配概率; 随机初始化关联矩阵a, 并求得相应的关联代价矩阵C如下:

$\begin{matrix} \begin{matrix} a = [\begin{matrix} 1 & 1 & 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 & 1 \end{matrix}] \\ C = \\ [\begin{matrix} 0.0038 & 0.1075 & 0.1204 & 0.0460 & 0.1559 & 0.0750 \\ 0.1071 & 0.0033 & 0.0213 & 0.0649 & 0.2660 & 0.0505 \\ 0.1157 & 0.0214 & 0.0016 & 0.0741 & 0.2728 & 0.0672 \\ 0.0391 & 0.0652 & 0.0790 & 0.0041 & 0.1982 & 0.0384 \\ 0.1600 & 0.2637 & 0.2744 & 0.2022 & 0.0008 & 0.2295 \\ 0.0743 & 0.0461 & 0.0671 & 0.0390 & 0.2310 & 0.0024 \end{matrix}] \end{matrix} \end{matrix}$

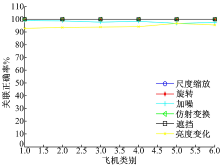
然后构造整体关联代价矩阵目标函数, 利用改进的模拟退火算法寻优, 得到使得ACM能量最小的关联矩阵 $\begin{matrix} \tilde{a} \end{matrix}$ 。此外, 提取出MSA特征后, 利用最近邻(NN)算法进行关联实验, 与得到的最终关联矩阵 $\begin{matrix} {\tilde{a}}_{NN} \end{matrix}$ 作比较。由于仿真图像目标组与原始目标组的排列顺序一样, 只对每个目标图像进行变换、加入干扰等, 理论上求得的最终关联矩阵 $\begin{matrix} \tilde{a} \end{matrix}$ 应该是单位矩阵。实验结果与理论一致, 可见利用关联代价矩阵最优化能够克服多目标特征匹配引起的关联模糊性, 关联结果更加准确。

$\begin{matrix} \begin{matrix} \tilde{a} & = [\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{matrix}] \\ {\tilde{a}}_{NN} & = [\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{matrix}] \end{matrix} \end{matrix}$

引入关联正确率指标进行统计实验分析, 图4给出了结合MSA特征和ACM最优化的多目标关联结果, 图5给出了结合MSA特征和NN方法实现多目标关联的结果。可以看出, 本文基于MSA和ACM最优化的多目标关联算法结果明显优于利用最近邻算法进行关联的结果。当图像发生尺度缩放、旋转、噪声干扰、仿射变换、遮挡以及亮度变化等一系列变化时, 最近邻算法无法解决关联模糊性, 而ACM考虑了整体关联代价, 具有一定的抗模糊性, 可获得更为有效的关联结果。

	Figure Option View Download New Window
	图4 MSA+ACMFig.4 Association accurate ratio of MSA+ACM

	Figure Option View Download New Window
	图5 MSA+NNFig.5 Association accurate ratio of MSA+NN

参考文献[9]是用MSA特征和ACM最优化算法解决舰船目标的关联问题, 本文借鉴其思路, 将该算法应用于飞机图像的多目标关联问题上, 并着重对传统模拟退火算法进行了改进。利用本文改进的模拟退火算法和传统算法对每组目标群图像分别独立运行50次, 记录每组运行时间(s)和目标关联结果数据, 计算关联正确率(%), 进行统计分析, 其对比结果如表1所示。可以看出, 改进的模拟退火算法既保持了多目标关联结果的准确性, 又减少了计算量, 在时间性能(搜索效率)上有了较大的提高。

表1 传统SA和改进的SA实验结果对比 Table 1 Experiment comparison results of the traditional SA and improved SA

5 结束语

针对无法准确估计采样稀疏的遥感图像中目标的状态信息, 而利用图像特征匹配的目标关联算法又无法处理大场景中多个目标关联引起的模糊性的问题。本文研究了基于MSA特征和关联代价矩阵最优化的遥感图像多目标关联算法, 并着重改进了模拟退火算法寻优过程。通过仿真实验表明:MSA特征可克服遥感成像中视点变化或目标姿态变化等因素的影响, 具有良好的仿射不变性和抗干扰性, 是有效的关联量; 在关联准则的约束下构造目标函数对ACM进行最优化, 得到的全局最优解有效消除了多目标之间特征关联的模糊性; 改进的模拟退火算法能够改善执行多次迭代搜索过程的时效性, 可快速得到全局最优解。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	雷琳. 多源遥感图像舰船目标特征提取和融合技术研究[D]. 长沙: 国防科技大学电子科学与工程学院, 2008. Lei Lin. Ship feature extraction and fusion in multiple remote sensing images[D]. Changsha: School of Electronic Science and Engineering, National University of Defense Technology, 2008. [本文引用:1]
[2]	Bar-shalom Y, Sherlukde H M, Pattipati K R. Use of measurements from an image sensor for precision target tracking[J]. IEEE Trans AES, 1989, 25(6): 863-871. [本文引用:1]
[3]	Bar Shalom Y. Extension of the probabilistic data association filter in multi-target tracking[C]∥Proceedings of the 5th symposium on nonlinear estimation, 1974: 16-21. [本文引用:1]
[4]	Blackman S, Dempster R J, Broida T J. Multiple hypothesis track confirmation for infrared surveillance systems[J]. IEEE Trans AES, 1993, 29(3): 810-823. [本文引用:1]
[5]	董学志, 宋建中, 韩广良. 一种利用Gabor小波特征的目标跟踪方法[J]. 光学技术, 2003, 29(4): 484-486. Dong Xue-zhi, Song Jian-zhong, Han Guang-liang. Target tracking method using wavelet feature[J]. Optical Technique, 2003, 29(4): 484-486. [本文引用:1]
[6]	姚剑, 刘其真, 张斌. 模糊技术与神经网络的混合算法在运动目标识别与跟踪中的应用[J]. 计算机工程与应用, 2000, 1: 62-64. Yao Jian, Liu Qi-zhen, Zhang Bin. The application of combination of fuzzy algorithms and neural network in tracking moving object[J]. Computer Engineering and Applications, 2000, 1: 62-64. [本文引用:1]
[7]	Hu M K. Pattern recognition by moment invariant[C]∥Proc IRE, 1961, 49: 1428-1436. [本文引用:1]
[8]	Rahtu E, Salo M, Heikkila J. Affine invariant pattern recognition using multi-scale auto convolution[J]. IEEE Transactions on Pattern analysis and Machine Intelligence, 2005, 27(6): 908-918. [本文引用:2]
[9]	雷琳, 蔡红苹, 唐涛, 等. 基于MSA特征的遥感图像多目标关联算法[J]. 遥感学报, 2008, 12(4): 586-592. Lei Lin, Cai Hong-ping, Tang Tao, et al. A MSA feature-based multiple targets association algorithm in remote sensing images[J]. Journal of Remote Sensing, 2008, 12(4): 586-592. [本文引用:1]
[10]	Bar-Shalom Y, Kirubarajan T, Gokberk C. Tracking with classification aided multiframe data assoeiation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(3): 868-878. [本文引用:1]
[11]	Mand al A K, Pal S, De A K, et al. Novel approach to identify good tracer clouds from a sequence of satellite images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 813-818. [本文引用:1]
[12]	Krickpatric S, Gelett J C D, Vecchi M P. Optimization by simulated annealing[J]. Science, 1983, 220(4598): 671-680. [本文引用:2]
[13]	Winkler G. Image Analysis, Rand om Fields and Dynamic Monte Carlo Methods[M]. Berlin: Springer-Verlag, 1999. [本文引用:1]
[14]	高尚. 模拟退火算法中的退火策略研究[J]. 航空计算技术, 2002, 32(4): 20-26. Gao Shang. Research on annealing strategy in simulated annealing algorithm[J]. Aeronautical Computer Technique, 2002, 32(4): 20-26. [本文引用:1]

2008

0.0

... 0 引言多源遥感图像融合^[1]能够综合利用多源互补的图像信息以提高信息的准确性与可靠性,因此在诸多领域得到广泛应用,包括军事、测绘、地质、农业及灾情监测等 ...

1989

0.0

1974

0.0

... 如文献[2]提出了基于目标质心及质心偏移量的联合概率数据关联(Joint probabilistic data association,JPDA)方法,首先将目标与背景分割,然后计算目标区域的质心,以估计目标的运动信息,最后利用JPDA方法^[3]实现关联与跟踪 ...

1993

0.0

2003

0.0

2000

0.0

. 2000, 1:62-64

The application of combination of fuzzy algorithms and neural network in tracking moving object

模糊技术与神经网络的混合算法在运动目标识别与跟踪中的应用

Yao Jian , Liu Qi-zhen , Zhang Bin.

姚剑, 刘其真, 张斌

图象跟踪是运动图象处理中的关键环节,但是如何在强噪声下实现快速有效的图象跟踪却一直是难点.该文提出了一种模糊技术与神经网络结合的算法,它充分吸收了模糊算法与神经网络的优点,在近距离目标下以神经网络识别的静态可能性为主,而在远距离目标时以模糊算法识别的动态可能性为主,使其不仅在目标近即大时有很高的识别率,而且更令人鼓舞的是在目标远即几乎为点目标时也有很高的识别率.另外,该文还提出了计算各个目标优先级的算法.最后,以红外序列图象为例表明该文提出的算法的高识别率.

1961

0.0

... 不变矩方法是解决图像特征不变性的常用方法,它能够克服视点变化对特征量的干扰,最具代表性的就是Hu矩特征^[7] ...

2005

0.0

... 2005年Rahtu等^[8]结合多尺度几何分析方法,在Hu矩特征的基础上,研究了可以同时捕获空间特性和图像强度的多维不变描述子,构造了多尺度自卷积矩(Multi scale autoconvolution,MSA)特征,实践证明这是目前最稳健的不变矩特征之一^[8] ...

2008

0.0

. 2008, 12(4):586-592

A MSA feature-based multiple targets association algorithm in remote sensing images

基于MSA特征的遥感图像多目标关联算法

Lei Lin , Cai Hong-ping , Tang Tao

雷琳, 蔡红苹, 唐涛

遥感图像中多目标关联存在以下两个问题:一是低时间分辨率观测使得目标状态信息无法准确估计,基于Kalman滤波的多目标关联算法不再适用;二是基于图像特征的目标关联算法又无法处理大场景观测中多个目标关联引起的模糊性.针对上述问题,提出一种基于多尺度自卷积特征匹配和关联代价矩阵最优化的多目标关联算法.实验表明该算法对遥感图像中多目标关联问题具有一定的适用性.

2005

0.0

... 1 构造ACM研究两幅遥感图像中的目标关联问题,可将其看作2维分配问题^[10] ...

2005

0.0

... 目标函数的最小值对应关联代价矩阵的最优解,即关联代价矩阵的能量最小^[11] ...

1983

0.0

... 模拟退火算法^[12](Simulated annealing,SA)是基于Monte-Carlo迭代求解策略的一种随机寻优算法,它来源于对固体退火过程的模拟,挖掘物理工程中固体物质的退火降温过程与组合优化问题的相似性,从理论上来说,它是一种近似全局最优算法 ...

... 1983年,Krickpatric等人将模拟退火算法成功应用于大规模组合优化问题的求解^[12] ...

1999

0.0

... 上述接受新状态的准则称Metropolis准则^[13],相对Monte Carlo方法来说,计算量明显减少 ...

2002

0.0

... 2 改进模拟退火算法寻优模拟退火算法是一种启发式搜索方法,它具有原理简单、适合求解组合优化问题中的全局(或近似)最优解^[14]、适用范围广等优点,但也存在一些缺点:当变量过多、构造的目标函数较复杂时,为获得较精确的全局最优解,初始温度需要足够高且降温幅度要小,这将导致迭代搜索过程缓慢,求解时间太长,工业应用较困难 ...