结合噪声去除的极大似然图像复原

引用本文

姜超, 耿则勋, 刘立勇, 潘映峰. 结合噪声去除的极大似然图像复原. 2015, 45(4): 1360-1366
JIANG Chao, GENG Ze-xun, LIU Li-yong, PAN Ying-feng. Maximum likelihood image restoration combined with image denoising. Journal of Jilin University Engineering and Technology Edition, 2015, 45(4): 1360-1366 复制到剪切板

Permissions

结合噪声去除的极大似然图像复原

姜超¹, 耿则勋¹, 刘立勇², 潘映峰³

1.解放军信息工程大学地理空间信息学院,郑州 450052

2.中国科学院国家天文台,北京 100012

3. 中国人民解放军61175部队,南京 210049

作者简介:姜超(1985-),男,博士研究生.研究方向:数字图像处理.E-mail:jiangchao19850429@126.com

基金:“863”国家高技术研究发展计划项目(2012AA7032031D); 国家自然科学基金项目(11373043)

摘要

基于混合噪声模型的极大似然算法不仅没有充分考虑迭代过程中的噪声影响,而且假定点扩散函数(PSF)已知且不随迭代过程变化,从而导致复原过程不稳定。在图像含噪且PSF未知的情况下,提出以去噪算法作为预处理手段,同时将PSF参数估计引入极大似然算法迭代过程并随迭代过程动态更新,最后将估计的PSF代入维纳滤波以提高复原图像的质量。实验结果证明,本文复原图像质量有明显改善,表明该算法具有较强的稳定性和抗噪声能力,是一种有效的图像复原方法。

关键词: 摄影测量与遥感技术; 图像复原; 混合噪声模型; 图像去噪; 点扩散函数; 极大似然

中图分类号:TP751 文献标志码:A 文章编号:1671-5497(2015)04-1360-07

Maximum likelihood image restoration combined with image denoising

JIANG Chao¹, GENG Ze-xun¹, LIU Li-yong², PAN Ying-feng³

1.PLA Information Engineering University, Zhengzhou 450052, China

2.National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012

3.Troops 61175 of PLA, Nanjing 210049, China

Abstract

In the maximum likelihood algorithm proposed by Benvenuto base on mixed noise model, the noise effect during iteration is not taken into consideration and the Point Spread Function (PSF) is assumed to be known and unchanged. This leads to the unstability of the image restoration. Under the condition of noise existence and PSF unknown, an image denoising algorithm is proposed as preprocessing, and the parameter estimation of PSF is introduced into iteration of the maximum likelihood and is dynamically updated. Finally, the Wiener filter with estimated PSF is utilized to improve the quality of the restored image. Experiment result demonstrate that the quality of the restored image is obviously improved, which proves the stability and noise resistance of the proposed algorithm.

Keyword: photogrammetry and remote sensing technology; image restoration; mixed noise model; image denoising; point spread function; maximum likelihood

Show Figures

0 引言

光学探测装置(如航空航天光学成像传感器和地基光学望远镜)透过大气对感兴趣目标进行观测时通常会受到大气湍流和噪声的干扰。这种干扰会造成观测目标图像质量严重退化, 影响后续的目标提取和识别等操作。为了解决大气湍流引起的图像模糊问题, 早期的研究人员提出了逆滤波、卡尔曼滤波以及维纳滤波等方法, 但上述滤波算法要求退化图像的点扩散函数(Point spread function, PSF)极大似然估计算法(Maxium likelihood, ML), 其中PSF是精确已知的。然而, 建立一个精确的数学模型来描述高度随机的大气湍流运动是非常困难的。因此, 在PSF未知或部分已知的情况下, 通常采用盲解卷积技术对目标图像和点扩散函数进行估计。常用的盲解卷积算法有:迭代盲解卷积(Iterative blind deconvolution, IBD)、非负支持域递归逆滤波(Non-negativity and support constraints recursive inverse filtering, NAS-RIF)、模拟退火算法(Simulated annealing, SA)以及极大似然估计算法。其中, IBD算法需要对PSF的支持域进行较紧的约束且算法的收敛性不够好, 通常只能得到一个近似的解^[1]。SA算法虽然具有全局收敛性, 但因该算法计算量过大, 而严重限制了其适用范围^[2]。NAS-RIF算法需要先确定目标的支持域并假定理想图像非负, 其对背景均匀的退化图像能取得较好的复原效果, 但该算法对噪声敏感^[3]。基于ML的盲解卷积算法是建立在真实的成像模型基础上的一种简单实用的最优化方法; 通过对解施加约束可以对该算法进行扩展, 从而推导出其他算法。2008年, Benvenuto等^[4]在传统ML算法的基础上提出了基于混合噪声模型的ML算法并证明了解的存在性。但该算法没有充分考虑迭代过程中的噪声影响, 同时假定PSF已知且在迭代过程中保持不变, 从而导致复原结果对噪声敏感且依赖于PSF的初始估计。

作者针对Benvenuto算法的不足, 首先, 对图像进行去噪预处理; 其次, 加入新的PSF迭代公式, 并随迭代过程动态更新PSF, 同时对目标估计图像去噪, 在降低对PSF初始估计依赖的同时增强算法的抗噪性; 最后, 将估计的PSF代入维纳滤波以进一步提高复原图像的质量。

1 混合噪声模型的极大似然算法

通常情况下, 传感器成像平面图像信号的数学模型可表示为:

$\begin{matrix} y_{i} = y_{i}^{obj} + y_{i}^{back} + y_{i}^{ron} (1) \end{matrix}$

式中:y_i是成像平面的第i个像素值; $\begin{matrix} y_{i}^{obj} \end{matrix}$ 和 $\begin{matrix} y_{i}^{back} \end{matrix}$ 分别表示目标辐射和背景辐射产生的光电子数量, 均服从泊松分布, 其数学期望分别为(Hx)_i和b_i, 令总光电子数量n_i= $\begin{matrix} y_{i}^{obj} \end{matrix}$ + $\begin{matrix} y_{i}^{back} \end{matrix}$ , 服从泊松分布; $\begin{matrix} y_{i}^{ron} \end{matrix}$ 为读出噪声, 这里假定其为均值r=0、方差σ ²的高斯白噪声。根据泊松分布原理有:

$\begin{matrix} P (n_{i} | {(Hx + b)}_{i}) = \frac{1}{n_{i}!} {(Hx + b)}_{i}^{n_{i}} e^{- {(Hx + b)}_{i}} (2) \end{matrix}$

传感器输出图像时, n_i受到读出噪声 $\begin{matrix} y_{i}^{ron} \end{matrix}$ 的污染, 最终的像素值y_i服从如下概率分布:

$\begin{matrix} P (y_{i} | n_{i}) = \frac{1}{\sqrt[]{2 π} σ} e^{- (y_{i} - n_{i})^{2} / (2 σ^{2})} (3) \end{matrix}$

由式(2)(3)可得泊松-高斯混合噪声模型下图像像素值的概率密度函数为:

$\begin{matrix} \begin{matrix} p_{Y} (y; x) = \\ \prod_{i \in S} (\overset{+ \infty}{\sum_{n = 0}} P (y_{i} | n_{i}) P (n_{i} | {(Hx + b)}_{i})) = \\ \prod_{i \in S} (\overset{+ \infty}{\sum_{n = 0}} \frac{1}{n!} {(Hx + b)}_{i}^{n} e^{- {(Hx + b)}_{i}} \frac{1}{\sqrt[]{2 π} σ} e^{\frac{(y_{i} {- n)}^{2}}{2 σ^{2}}}) (4) \end{matrix} \end{matrix}$

为了计算理想目标图像的极大似然估计, 对式(4)取负对数可得:

$\begin{matrix} \begin{matrix} J (x) = - \ln (p_{Y} (y; x)) = \\ - \sum_{i \in S} \ln \{\overset{+ \infty}{\sum_{n = 0}} \frac{{(Hx + b)}_{i}^{n}}{n!} e^{- {(Hx + b)}_{i}} \frac{1}{\sqrt[]{2 π} σ} e^{\frac{(y_{i} {- n)}^{2}}{2 σ^{2}}}\} = \\ \sum_{i \in S} \{{(Hx + b)}_{i} - \ln \overset{+ \infty}{\sum_{n = 0}} \frac{1}{n!} {(Hx + b)}_{i}^{n} e^{- \frac{(y_{i} {- n)}^{2}}{2 σ^{2}}}\} (5) \end{matrix} \end{matrix}$

将式(5)两边对待估像素值求导数, 可得:

$\begin{matrix} \nabla J (x) = h - H^{T} \frac{q (x)}{p (x)} (6) \end{matrix}$

式中:h= $\begin{matrix} \sum_{i \in S} \end{matrix}$ H_i; H为点扩散函数PSF的傅里叶变换; 向量p(x)和q(x)中的元素值分别为:

$\begin{matrix} \begin{matrix} p_{i} (x) = \overset{+ \infty}{\sum_{n = 0}} \frac{{(Hx + b)}_{i}^{n}}{n!} e^{- \frac{1}{2 σ^{2}} (n - y_{i})^{2}} (7) \\ q_{i} (x) = \overset{+ \infty}{\sum_{n = 0}} \frac{{(Hx + b)}_{i}^{n - 1}}{(n - 1)!} e^{- \frac{1}{2 σ^{2}} (n - y_{i})^{2}} = \\ \overset{+ \infty}{\sum_{n = 0}} \frac{{(Hx + b)}_{i}^{n}}{n!} e^{- \frac{1}{2 σ^{2}} (n + 1 - y_{i})^{2}} (8) \end{matrix} \end{matrix}$

在式(1)确定的成像模型中, 并不能确保各像点的像素值都为正值, 这是因为当背景的灰度值接近或等于零时, 由于加性高斯噪声的污染导致噪声点的像素值可能为负值。然而, 图像复原的目标就是得到观测目标图像的最优非负估计, 由此可得极大似然算法计算步骤:

Step1 给定初始值, 满足条件x⁰≥ 0。

Step2 由上式给定的初值按下式迭代计算。

$\begin{matrix} x^{k + 1} = \frac{x^{k}}{h} H^{T} \frac{q (x^{k})}{p (x^{k})} (9) \end{matrix}$

通常情况下, 式(9)要经过多次迭代方能得到较好的复原结果, 但其计算量非常大, 使得传统极大似然算法效率低下。文献[4]提出了式(9)的等效近似模型, 将参数b和σ ²引入该式, 以表达泊松-高斯混合噪声的影响, 最终的迭代公式为:

$\begin{matrix} x^{k + 1} = \frac{x^{k}}{h} H^{T} \exp [- \frac{1 + 2 (H x^{k} + b - y)}{2 (H x^{k} + b + σ^{2})}] (10) \end{matrix}$

大量实验表明, 用式(10)形成的极大似然迭代算法对符合泊松高斯混合噪声模型的退化图像有较好的重建效果。但是随着迭代次数的增加, 算法收敛的稳定性快速下降, 同时, 由于迭代过程中没有考虑噪声的影响, 明显出现噪声放大的现象。此外, 该算法假设PSF已知, 且在整个迭代过程中保持不变, 所以PSF初值的选取严重影响算法收敛的稳定性。在PSF未知的情况下, 很难得到目标图像的最优估计。本文将针对Benvenuto算法的不足, 加入去噪算法对含噪图像进行预处理, 并且在算法迭代过程中对估计目标图像进行去噪, 降低噪声对算法稳定性的影响; 其次, 在迭代过程中加入PSF的迭代公式, 同时对其进行正性约束和归一化约束, 使得复原结果不严重依赖于PSF初值的选取, 保证复原结果的可靠性; 最后, 将最终估计的PSF代入维纳滤波, 以避免估计图像强度集中。

2 图像去噪算法简介与对比

图像复原的实质就是恢复退化图像中的高频信息, 但是噪声也属图像中的高频信息, 对含噪图像进行复原操作将不可避免地产生噪声放大的现象。为了解决该问题, 在复原操作前对含噪图像进行去噪预处理是一种可行的方案。本文简要介绍当前使用最为广泛的四种去噪算法(总变分去噪(Total variation, TV)、贝叶斯最小二乘-高斯尺度混合去噪(Bayes least squares-gaussian scale mixtures, BLS-GSM)、非局部均值去噪(Non-local means, NLM)以及块匹配3D滤波去噪(Block-matching and 3D filtering, BM3D)), 并对算法的去噪性能进行对比分析。详细的算法原理见文献[5-8]。

2.1 TV去噪

Rudin等^[5]于1992年提出了TV去噪模型, 该模型采用能量函数的最小化问题来对图像去噪进行建模, 并在去噪处理中引入偏微分方程的各向异性扩散方程, 在抑制图像噪声的同时可以保持边缘, 较好地解决了抑制噪声和图像边缘保持之间的矛盾。

2.2 BLS-GSM去噪

Portilla等^[6]于2003年提出BLS-GSM去噪算法, 该去噪算法主要包括3个步骤^{[3, 4]}:①将图像在不同尺度和方向进行金字塔分解; ②对分解后的每一层进行去噪; ③用处理后的分层重构图像并进行金字塔反变换得到去噪图像。

2.3 NLM去噪

2005年, Buades等^[7]提出NLM去噪算法, 该方法结合图像中的全局信息综合考虑图像噪声模型(用全部像素的加权平均来估计去噪后的像素值), 既消除了传统邻域滤波器中出现的伪影, 又可保持边缘细节, 同时利用图像自身的自相似性能较好地恢复图像。

2.4 BM3D去噪

2007年, Dabov等^[8]提出了一种理想的图像去噪方法— — BM3D。该方法不仅利用图像的自相似性和冗余性等信息, 而且结合了变换域的阈值方法, 是一种多尺度、非局部的去噪技术, 广泛应用于图像和视频的去噪。

2.5 对比分析

本文主要考察算法的去噪性能和处理效率, 因此分别记录4种算法的峰值信噪比(Peak signal-to-noise ratio, PSNR)和处理时间。为了比较在不同噪声强度下的去噪性能, 对原始图像分别施加标准差为10和30的随机噪声, 最终的结果如图1、图2及表1、表2所示。

	Figure Option View Download New Window
	图1 噪声标准差为10时的去噪情况Fig.1 Standard deviation when noise is 10

	Figure Option View Download New Window
	图2 噪声标准差为30时的去噪情况Fig.2 Standard deviation when noise is 30

通过上述图表可知, 以上4种算法在去噪质量上都能达到较好的效果, 除TV算法的PSNR值略低外, 其余3种算法的PSNR值相近; 在处理效率上, 由于NLM算法不仅需要计算邻域相似性的权值, 而且图像中的每一像素点要与所有像素点的邻域一一比较, 所以计算量非常大, 导致效率低下。另外3种算法效率相当, 其中BM3D和TV略有优势。综上所述, 考虑复原算法的效率和重建质量, 本文采用BM3D和TV算法作为去噪预处理算法。

表1 噪声标准差为10时的去噪情况 Table 1 Denoising results when noise variance is 10

表2 噪声标准差为30时的去噪情况 Table 2 Denoising results when noise variance is 30

3 改进的极大似然算法

由第2节讨论可知, Benvenuto等^[4]提出的基于混合噪声模型的极大似然算法存在以下两方面问题:迭代过程中没有考虑噪声的影响, 随着迭代次数的增加, 稳定性变差, 噪声放大现象加剧; 假定PSF已知, 且不随迭代过程动态更新, 导致复原结果严重依赖于PSF初始估计。在上一节中提出用相应的去噪算法对含噪图像作预处理, 并在迭代过程中对估计的目标图像进行去噪处理以解决该算法在迭代过程中对噪声敏感的问题。在本节中, 将引入新的PSF迭代公式, 以避免该算法对PSF初始估计的依赖。

式(1)中的噪声项{ $\begin{matrix} y_{i}^{back} \end{matrix}$ + $\begin{matrix} y_{i}^{ron} \end{matrix}$ }符合泊松高斯混合噪声模型, 对应的概率密度函数为:

$\begin{matrix} p (y, b, σ) = \overset{+ \infty}{\sum_{n = 0}} \frac{1}{n!} b^{n} e^{- b} \frac{1}{\sqrt[]{2} σ} e^{- {(y - n)}^{2} / {(2 σ)}^{2}} (11) \end{matrix}$

对于未知参数b和σ ², 采用矩估计法计算其估计值^[9], 分别记为 $\begin{matrix} \hat{b} \end{matrix}$ 和 $\begin{matrix} {\hat{σ}}^{2} \end{matrix}$ :

$\begin{matrix} \hat{b} = m_{1}, {\hat{σ}}^{2} = m_{2} - m_{1} (12) \end{matrix}$

式中:m₁= $\begin{matrix} \frac{\overset{N}{\sum_{k = 1}} y_{k}}{N} \end{matrix}$ ; m₂= $\begin{matrix} \frac{\overset{N}{\sum_{k = 1}} (y_{k} - m_{1})^{2}}{N} \end{matrix}$ , 其中{y_k, k=1, 2, …, N}表示原始图像中不包含目标背景区域的灰度值序列构成的列向量。

根据矩估计法得到的极大似然算法参数值, 结合式(10)得到一个对称的PSF迭代公式为:

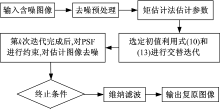
$\begin{matrix} H^{k + 1} = \frac{H^{k}}{h} {(x^{k})}^{T} \exp [- \frac{1 + 2 (H x^{k} + b - y)}{2 (H x^{k} + b + σ^{2})}] (13) \end{matrix}$

将式(10)和式(13)进行交替迭代, PSF的值会随着迭代过程动态更新, 有效克服了原算法对PSF初始估计的依赖, 实现真正的盲解卷积。另外, 在交替迭代过程中, 除了加入PSF正性约束和归一化约束外, 同时对目标估计进行去噪处理, 进一步保证了算法的稳定性及抗噪性。最后, 由式(10)和式(13)进行迭代得到的复原图像强度分布较集中, 这是因为极大似然算法是基于概率统计的方法, 只能最大似然地复原图像, 而不能很好地保持图像细节。为了克服该缺陷, 考虑在算法迭代完成后, 将估计的最终PSF代入维纳滤波算法, 以进一步提高复原图像质量。改进后的算法流程图如图3所示。

	Figure Option View Download New Window
	图3 改进的极大似然算法流程图Fig.3 Flow chart of improved ML algorithm

4 实验结果与分析

为验证本文算法的稳定性和抗噪性, 分别选取空间点源目标和扩展目标作为模拟数据进行图像复原实验, 图像大小为256× 256, 测试平台为Matlab7.14。采用带有泊松高斯混合噪声模型的长曝光大气湍流模型对原始图像进行降质处理, 其中, 光学系统长曝光OTF为:

$\begin{matrix} H_{LE} (v) = \exp \{- 3.44 {(\frac{λfv}{r_{0}})}^{\frac{5}{3}}\} (14) \end{matrix}$

式中:λ 表示波长; f表示望远镜焦距; r₀表示大气相干长度; v= $\begin{matrix} \sqrt[]{v_{u}^{2} + v_{v}^{2}} \end{matrix}$ 表示频率。

为客观评价算法的复原性能, 引入有参考图像评价指标相关系数和峰值信噪比以及无参考图像评价指标ImageQ对复原结果进行评价。其中, ImageQ综合考虑复原前后图像棱边区局部方差的平均增加量和平坦区局部方差的减少量来评价棱边恢复程度以及图像伪像的消除程度(原理见文献[10])。

峰值信噪比主要评价复原算法的抗噪性, 其值越大, 说明复原图像受噪声的影响越小, 其定义为:

$\begin{matrix} PSNR = 10 \lg (\frac{255 \times 255}{MSE}) (15) \end{matrix}$

相关系数通过计算复原图像与理想图像对应像点的差值, 反映两者之间的相似度, 相关系数趋近于1, 则表明复原结果与理想图像越接近, 复原效果越好; 反之, 两者之间的偏差越大, 复原效果越差。其定义为:

$\begin{matrix} c = \frac{E [(f - E (f)) (\hat{f} - E (\hat{f}))]}{\sqrt[]{E (f^{2}) - E {(f)}^{2}} \sqrt[]{E ({\hat{f}}^{2}) - E {(\hat{f})}^{2}}} (16) \end{matrix}$

4.1 模拟点源目标复原实验

	Figure Option View Download New Window
	图4 模拟点源目标复原结果对比Fig.4 Result comparison of simulated point source object

模拟双星图像的大气相干长度r₀=5 cm, 添加方差σ ²=0.05的高斯白噪声, 理想点源目标图像和模拟退化图像分别如图4(a)(b)所示。Benvenuto算法的结果如图4(c)所示, 本文算法的复原结果如图4(d)(e)所示; 评价指标如表3所示。

表3 双星图像评价指标对比 Table 3 Evaluation scales comparison of double-star image

4.2 模拟扩展目标复原实验

图5(a)为原始的Pleiades卫星图像, 采用大气相干长度r₀=10 cm, 方差σ ²=0.05的高斯白噪声对原始图像进行退化处理得到模拟退化图像如图5(b)所示。复原结果如图5(c)(d)(e)所示, 评价指标如表4所示。

	Figure Option View Download New Window
	图5 模拟扩展目标复原结果对比Fig.5 Result comparison of simulated satellite image

表4 扩展目标图像评价指标对比 Table 4 Evaluation scales comparison of satellite image

从图4、图5及表3、表4可以发现, 本文算法的各项评价指标较Benvenuto算法均有不同程度的提高, 证明了本文算法的可靠性和有效性。其中, 结合TV去噪的复原算法在PSNR和相关系数指标上均优于结合BM3D去噪的复原算法, 建议对复原图像细节信息恢复要求较高的情况下使用; 结合BM3D去噪的复原算法在复原图像视觉效果上有明显优势, 背景噪声去除效果最好, 但同时也损失了部分目标细节信息, 建议在对复原图像视觉效果要求较高的情况下使用。

5 结束语

由于Benvenuto提出的基于泊松高斯混合噪声模型的极大似然算法存在两个方面的缺陷:没有充分考虑迭代过程中的噪声影像; 要求PSF已知, 且在迭代过程中保持不变。这使得复原结果对噪声敏感且严重依赖于PSF的初始估计。作者针对以上问题, 提出结合噪声去除的改进极大似然算法。首先, 采用去噪算法对含噪图像进行预处理; 其次, 加入新的PSF迭代公式并随迭代过程动态更新, 同时对估计目标图像进行去噪, 以减轻噪声对迭代过程的影响; 最后, 将估计的PSF代入维纳滤波, 进一步改善复原质量。实验证明, 本文算法有效克服了复原过程中的噪声放大以及对PSF初始估计的依赖性, 复原质量有明显改善, 可以作为一种有效的复原方法用于观测图像的高清晰重建。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Ayers C R, Dainty J C. Iterative blind deconvolution method and its application[J]. Optics Letters, 1988, 13(7): 547-549. [本文引用:1]
[2]	Maccallum B C. Blind deconvolution by simulated annealing[J]. Optics Communication, 1990, 75(2): 101-105. [本文引用:1]
[3]	Kundur D, Hatzinakos D. Blind image deconvolution[J]. IEEE Single Processing Magazine, 1996, 13(3): 43-64. [本文引用:2]
[4]	Benvenuto F, Camera A L. The study of an iterative method for the reconstructionof images corrupted by Poisson and Gaussian noise[J]. Inverse Problems, 2008, 24(3): 35016-35035. [本文引用:3]
[5]	Rudin L I, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms[J]. Physica D: Nonlinear Phenomena, 1992, 60: 259-268. [本文引用:1]
[6]	Portilla J, Strela V, Wainwright M J, et al. Image denoising using Gaussian scale mixtures in the wavelet domain[J]. IEEE Trans Image Processing, 2003, 12(11): 1338-1351. [本文引用:1]
[7]	Buades A, Coll B, Morel J M. A non local algorithm for image denoising[J]. IEEE Computer Vision and Pattern Recognition, 2005, 2: 60-65. [本文引用:1]
[8]	Dabov K, Foi A, Katkovnik V, et al. Image denoising by sparse 3D transform-domain collaborative filtering[J]. IEEE Trans Image Process, 2007, 16(8): 2080-2095. [本文引用:1]
[9]	周宏潮, 朱炬波, 王正明. 混合泊松-高斯分布模型的参数估计[J]. 中国空间科学技术, 2005, 25(2): 1-5. Zhou Hong-chao, Zhu Ju-bo, Wang Zheng-ming. Parametric estimation of mixed Poisson-Gaussian distribution model[J]. Chinese Space Science and Technology, 2005, 25(2): 1-5. [本文引用:1]
[10]	陈波. 自适应光学图像复原理论与算法研究[D]. 郑州: 解放军信息工程大学, 2008: 63-68. Chen Bo. The theory and algorithms of adaptive optics image restoration[D]. Zhengzhou: PLA Information Engineering University, 2008: 63-68. [本文引用:1]

1988

0.0

... 其中,IBD算法需要对PSF的支持域进行较紧的约束且算法的收敛性不够好,通常只能得到一个近似的解^[1] ...

1990

0.0

... SA算法虽然具有全局收敛性,但因该算法计算量过大,而严重限制了其适用范围^[2] ...

1996

0.0

... NAS-RIF算法需要先确定目标的支持域并假定理想图像非负,其对背景均匀的退化图像能取得较好的复原效果,但该算法对噪声敏感^[3] ...

... 2 BLS-GSM去噪Portilla等^[6]于2003年提出BLS-GSM去噪算法,该去噪算法主要包括3个步骤^[3,4]:①将图像在不同尺度和方向进行金字塔分解 ...

2008

0.0

... 2008年,Benvenuto等^[4]在传统ML算法的基础上提出了基于混合噪声模型的ML算法并证明了解的存在性 ...

... 2 BLS-GSM去噪Portilla等^[6]于2003年提出BLS-GSM去噪算法,该去噪算法主要包括3个步骤^[3,4]:①将图像在不同尺度和方向进行金字塔分解 ...

... 3 改进的极大似然算法由第2节讨论可知,Benvenuto等^[4]提出的基于混合噪声模型的极大似然算法存在以下两方面问题:迭代过程中没有考虑噪声的影响,随着迭代次数的增加,稳定性变差,噪声放大现象加剧 ...

1992

0.0

... 1 TV去噪Rudin等^[5]于1992年提出了TV去噪模型,该模型采用能量函数的最小化问题来对图像去噪进行建模,并在去噪处理中引入偏微分方程的各向异性扩散方程,在抑制图像噪声的同时可以保持边缘,较好地解决了抑制噪声和图像边缘保持之间的矛盾 ...

2003

0.0

... 2 BLS-GSM去噪Portilla等^[6]于2003年提出BLS-GSM去噪算法,该去噪算法主要包括3个步骤^[3,4]:①将图像在不同尺度和方向进行金字塔分解 ...

2005

0.0

... 3 NLM去噪2005年,Buades等^[7]提出NLM去噪算法,该方法结合图像中的全局信息综合考虑图像噪声模型(用全部像素的加权平均来估计去噪后的像素值),既消除了传统邻域滤波器中出现的伪影,又可保持边缘细节,同时利用图像自身的自相似性能较好地恢复图像 ...

2007

0.0

... 4 BM3D去噪2007年,Dabov等^[8]提出了一种理想的图像去噪方法#cod#x02014 ...

2005

0.0

. 2005, 25(2):1-5 DOI:doi:10.3321/j.issn:1000-758X.2005.02.001

Parametric estimation of mixed Poisson-Gaussian distribution model

混合泊松-高斯分布模型的参数估计

Zhou Hong-chao , Zhu Ju-bo , Wang Zheng-ming.

周宏潮, 朱炬波, 王正明

针对实际CCD图像处理问题中噪声概率模型的参数估计问题,从CCD图像的噪声背景出发,研究其噪声的混合泊松-高斯分布,给出了两种参数估计方法,以及非零均值高斯噪声情况下的参数估计方法,计算结果表明文中方法给出的参数估计精度高.

... ²,采用矩估计法计算其估计值^[9],分别记为 b^和 σ^2: ...

2008

0.0

. 2008, :63-68

The theory and algorithms of adaptive optics image restoration

自适应光学图像复原理论与算法研究[D]

Chen Bo.

陈波

通过大气湍流成像是所有工作在大气环境中的光学成像系统必然会遇到的问题。在光线进入成像传感器入瞳之前,大气介质影响或干扰光波的理想传播,使目标反射电磁波的波阵面产生畸变,形成焦平面上像点强度分布扩教、峰值降低以及光束漂移等湍流效应,最终导致图像模糊,严重地影响光学系统的成像性能。自适应光学技术是目前克服大气湍流最有效的方法之一,但其对大气湍流的补偿是不完全的,目标的高频信息仍然受到抑制和衰减。因此,对经过自适应光学校正后的图像还必须进行基于图像复原技术的后处理,才能获取更清晰的目标图像。本文主要针对我国自适应光学地基望远镜成像后处理的迫切需求,利用信号处理和计算机软件技术对图像进行高清晰复原,以消除自适应光学校正的残余误差,使其接近或达到成像系统的衍射极限。论文重点研究了自适应光学图像复原理论与算法,同时对自适应光学波前重构和图像复原质量评价等问题也进行了探讨与分析,完成的工作主要包括: 1.开发了自适应光学成像原理演示系统。根据光波大气湍流传输理论,分别分析了湍流对长曝光OTF和短曝光OTF的影响。在介绍自适应光学系统组成和工作原理的基础上,基于SCIAO平台设计一个简单的自适应光学成像原理演示系统CYAOIS。 2.定义了图像复原质量综合评价指数。针对现有图像复原质量评价方法没有考虑伪像的不足,根据人眼视觉的特点,定义了一种基于分区局部方差变化统计的图像复原质量综合评价指数。实验证明,该指数是无参考图像复原质量评价的一种客观有效的指标。 3.基于广义岭估计的自适应光学图像波前重构。从自适应光学图像后处理复原的角度来讲,实时性和快速计算不再是波前重构的基本要求,而高精度才是波前重构最重要的要求。按照时间换精度的思路把广义岭估计GRE和迭代答解的思想引入波前重构,提出一种面向图像复原的广义岭估计Zernike模式波前重构算法。实验证明,该算法重构的PSF在图像复原中有更好的图像重建效果。 4.非抽样小波变换降质图像PSF估计。在图像复原问题中,PSF估计是算法的核心部分。把非抽样小波变换引入降质图像PSF估计,在Fried参数模型的基础上,根据不同尺度下小波变换模极大值和高斯点扩展函数方差的关系,提出一种基于非抽样小波变换的PSF估计算法。实验结果证明,该算法对无波前测量数据自适应光学图像有较好的PSF估计精度。 5.基于ENAS-RIF算法的自适应光学图像复原。针对基本NAS-RIF算法的不足,把Curvelet去噪图像预处理、可靠支持域、目标结构约束项和增强代价函数引入NAS-RIF算法,提出了基于可靠支持域和改进代价函数的ENAS-RIF算法。自适应光学图像复原实验结果证明,ENAS-RIF 算法较之NAS-RIF算法有更快的收敛速度、更好的恢复效果。 6.基于IRL-IBD算法的自适应光学图像复原。在非对称IBD算法的基础上,本文在PSF频率域引入带宽有限约束来进一步提高算法的可靠性,在PSF 像素空间引入动态支持域的思想以加快算法收敛速度,提出多重约束非对称IRL-IBD算法用于自适应光学图像高清晰复原。实验结果证明,改进后的IRL- IBD算法复原性能明显优于IBD算法。 7.基于方差统计的图像序列不良帧剔除。在多帧图像高清晰复原中,一些降质严重的观测图像不但不能对复原作出贡献,而且将可能严重影响重建图像的质量。本文利用加性噪声导致降质图像方差增大和PSF模糊导致降质图像方差减小的性质,参考摄影测量中粗差剔除的思想,设计了一个基于图像方差统计的不良帧自动剔除方案。实验结果表明,剔除不良帧后的图像复原效果有明显改善。 8.基于MAP原理的自适应光学图像多帧MF-MAPJD高清晰复原。在Bayesian框架下,根据自适应光学图像的特点重新定义了混合噪声模型和目标结构先验模型,在代价函数中新增加了PSF准则项,设计了一个简单的正则化约束项自动平衡方案,提出了基于MAP原理的AO图像多帧联合解卷积算法MF- MAPJD。实验结果表明,新算法同时估计点扩教函数和目标,充分了利用图像序列中的各种先验约束信息,复原图像质量改善明显。 9.基于二代Curvelet变换的图像自适应去噪。利用Curvelet变换比小波变换对图像信号具有更稀疏表示的特点,结合Bayesian Shrink理论,提出了一种改进的Curvelet域图像自适应去噪算法。实验结果表明其去噪性能优予小波去噪算法。 10.基于二代Curvelet变换的自适应光学图像复原。把多尺度多方向的思想引入自适应光学图像处理,设计了基于二代Curvelet变换的 Fourier-Curvelet混合域正则化图像复原算法ForCuRD。ForCuRD算法同时采用了傅里叶域收缩和Curvelet域收缩,克服单一变换域收缩的局限,为自适应光学图像复原研究提供了一条新思路。