作者简介:左曙光(1968-),男,教授,博士生导师.研究方向:汽车振动与噪声控制.E-mail:sgzuo@tongji.edu.cn
针对车用驱动电机转矩波动引起悬架系统振动进而造成车内噪声的问题,提出通过改善悬架纵向和垂向振动传递特性来实现减振的优化方法。通过扭杆梁柔性化、高频衬套模型的ADAMS实现等措施保证悬架弹性元件的精确描述来建立适用于高频仿真的悬架模型,并基于此模型进行振动传递特性分析,最后基于ISIGHT集成多学科软件实现多目标全局优化。优化结果表明:在略微减小垂向振动传递函数加权面积的基础上使纵向振动传递函数加权面积减小了17.23%,且在目标频段内振动传递优化效果显著。
An optimization method was proposed to solve the vibration issue of suspension system in both vertical and longitude directions, which is commonly caused by torque ripple of wheel-drive motor in electric vehicle. By flexibly modeling of the twist beam and realizing the high-frequency bushing model in the ADAMS, the elastic component was accurately described, then, the high-frequency applied suspension model was built. Based on ISIGHT software, the multi-objective optimization was conducted by integrating multi-disciplinary software. The optimization results showed that the weighted area of longitudinal vibration transfer function was optimized by 17.23% with slightly reducing the weighted area of vertical vibration transfer function. Within the target spectrum, the optimizing effect of vibration transfer is significant.
与传统汽车不同, 轮边驱动电动车的悬架系统不仅要衰减来自路面不平的激励, 还需要缓解驱动电机带来的额外振动。同济大学研究小组的试验表明[1], 驱动电机的转矩波动会引起悬架系统振动进而造成车内噪声, 其频率分布覆盖30~280 Hz。目前, 针对转矩波动引起的悬架振动问题的研究及其优化仍然较少。文献[2-3]对某特定转速下的转矩波动激励引起的车身振动问题进行了优化, 获得了一定的优化效果; 同时也提及由于研究频率的提高, 需要对模型的精确建立提出更高的要求。而精确建模的关键在于弹性元件的精确描述。Dzierek[4]建立了基于试验的圆柱衬套模型应用于五连杆悬架模型中, 分析表明精确衬套模型的应用能提高传递函数的精度。文献[5]指出, 弹性元件(尤其是衬套模型)在中高频段(20 Hz以上)动特性的描述准确与否会对悬架系统传递特性分析带来较大的影响。因此, 在建模过程中精确反映弹性元件的特性是必要。
以往的试验研究表明, 转矩波动主要引起悬架和车身的纵向振动[6], 而传统的路面不平激励则要求悬架系统需要保持良好的垂向振动传递特性。因此, 该优化设计问题是一个多目标的优化问题。针对该类优化设计问题若采用传统的确定性优化方法只能进行局部优化, 而以遗传算法为代表的随机性方法不仅具有全局性优化特点, 而且算法的鲁棒性、可靠性均较好[7, 8, 9]。单纯基于传统多体软件(如ADAMS)无法满足以上多目标及全局优化两方面的要求, 而在航空航天领域应用较多的ISIGHT软件不仅可以实现多目标全局优化, 还可以集成多学科的软件, 为解决此类问题提供便利。
本文首先对某轮边驱动电动车扭杆梁悬架进行精确建模, 使其满足高频仿真分析需要, 然后利用模型进行振动传递特性的分析, 最后基于ISIGHT平台进行针对纵向和垂向振动传递特性的多目标优化设计, 并通过实测转矩波动信号激励验证其优化效果。
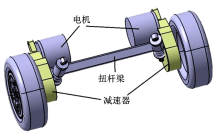
本文的研究对象来源于某轮边驱动电动汽车的后悬架, 主体结构为驱动电机、两级斜齿轮减速器和扭杆梁, 其中驱动电机与减速器固连, 减速器壳体同时也是悬架纵臂, 此外, 减振器与弹簧套连在一起连接于车身。三维实体结构如图1所示。
在模型建立之前需要明确模型的仿真频率范围, 即本文的研究频率范围。文献[1]通过试验发现, 在电动车的运行过程中加速和回馈制动时驱动电机的转矩波动引起车内噪声最为明显, 且主要频率为6倍电流频率。因此本文将所研究的工况选择在加速或者制动过程最常覆盖的车速10~50 km/h, 折算成转速约为100~500 r/min, 主要研究频率为电流频率的6倍频。其中电流频率可由下式计算得到[10]:
式中:p为电机极对数; n为电机转速; f为电流频率。
本文驱动电机为4对极, 可以计算得到当转速维持在100~500 r/min范围时, 电流频率将维持在6.667~33.333 Hz, 而6倍于电流频率则主要分布在40~200 Hz, 即本文振动衰减的目标频率范围为40~200 Hz。
建模过程中进行了扭杆柔性化和高频衬套的实现来描述弹性元件使其满足模型仿真频率最高达200 Hz的要求。
在传统低频研究过程中, 扭杆梁组件通过各向等效刚度来简要描述就能满足仿真需求。但是由于本文的分析频率较高, 为了能够精确反映悬架系统的模态信息, 需要将扭杆梁及纵臂进行柔性化。同时考虑到该悬架的纵臂同时也是减速器的壳体, 而壳体内部还支撑有轴系、齿轮和轴承等部件。若对整体进行柔性化势必会大大增加计算量, 且会给各部件间的连接关系描述带来困难, 故此处仅对扭杆梁进行柔性化。
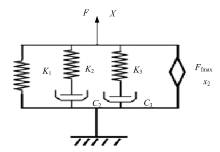
ADAMS中的衬套模型是简单的Kelvin-Voigt模型, 由一个刚度不变的弹簧和一个阻尼一定的粘壶组成, 其动力学方程如下:
式中:x为激励位移; K为刚度; C为阻尼; F为响应力。
该模型主要适用于较低频率的仿真(低于20 Hz), 应用于高频仿真时会高估阻尼的贡献, 从而产生较大误差[11]。
本文所采用的衬套模型是基于课题组之前关于橡胶衬套高频动态模型的研究[5], 根据玻尔兹曼叠加原理将描述不同橡胶材料特性的模型进行组合, 每个方向上都由1个超弹性单元、2个Maxwell黏弹性单元和1个摩擦单元组成, 得到其本构模型如图2所示。
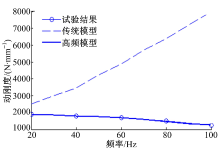
通过利用Fortran语言编写GFOSUB用户子程序来定义该橡胶衬套模型, 然后利用链接实现该衬套模型在ADAMS中的仿真调用。为了说明本文所建高频衬套模型在中高频仿真时的优势, 取轴向动刚度特性作对比, 但是由于激振台激振频率范围限制, 此处对比频率最高为100 Hz, 如图3所示。从图中可以看到, 高频衬套模型的动刚度特性与试验结果吻合较好, 且变化趋势相同, 而传统衬套模型会出现较大的偏差。因此将该高频模型在ADAMS悬架模型中实现将给模型的精确仿真带来极大的帮助。
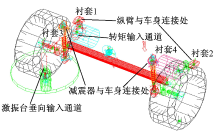
考虑到本文的仿真频率范围, 选择ADAMS中使用频率最高的FTire轮胎模型作为最终的轮胎模型[12]。最终在ADAMS/View中建立得到扭杆梁悬架系统刚柔耦合模型, 如图4所示。
一个振动系统的振动传递特性一般采用系统传递函数来表示。在电机输出位置— — 电机与悬架纵臂连接点建立转矩型输入通道, 输入幅值为100 N· m扫频转矩, 定义车身质心和衬套1~4的被动端处的纵向加速度为输出, 如图4所示。计算得到从电机与纵臂连接处到车身质心的无阻尼纵向传递函数, 如图5所示。从图中可以得到6个比较显著的峰值频率, 分别为16.59、17.69、29.39、71.96、105.30、134.51 Hz, 其中后3个峰值频率正好落在目标衰减频率范围。
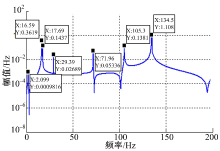 | 图5 电机与纵臂连接处到车身质心的无阻尼纵向传递函数Fig.5 Undamped longitudinal transfer function from motor and trailing arm joint to the body |
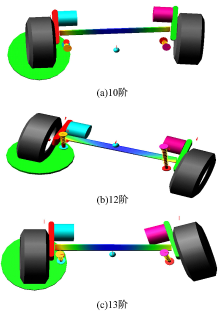
通过系统的模态计算发现, 在200 Hz以内系统总共有14阶模态。其中, 纵向传递函数中的后3个峰值频率分别对应系统第10、12、13阶模态的固有频率。观察该3阶模态的振型分别为:悬架前后移动、左右悬架上下反向跳动、右侧悬架绕Z轴摆动, 如图6所示。
为了避免共振的发生, 需要通过合理设计使得系统的固有频率尽可能与激励频率相错开。而通过振型动画可以发现, 10、12、13阶模态振型主要是由于扭杆梁的变形导致, 因此要想改变该频率段的模态频率分布, 从扭杆梁各向等效刚度的设计入手最为有效。
此外, 电机转矩波动引起的振动是通过悬架与车身连接的4个衬套传递给车身。衬套1、2分别为悬架左侧和右侧纵臂与车身连接衬套, 衬套3、4分别为悬架左侧和右侧减振器上支点与车身的连接衬套。在电机与纵臂连接处施加的白噪声扫频转矩激励下, 得到4个衬套处的纵向加速度响应功率谱密度如图7所示。从图中可以看到4个衬套的纵向加速度响应在不同频率段有不同的大小关系, 但是有一个共同点:纵臂与车身连接处衬套的纵向加速度响应幅值最大, 即衬套1、2纵向加速度的幅值大于衬套3、4纵向加速度的幅值。这说明电机转矩波动引起的纵向振动主要通过扭杆梁悬架纵臂与车身连接处的衬套传递到车身。
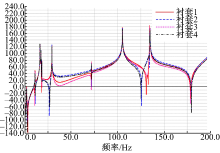 | 图7 白噪声转矩激励下4个衬套纵向加速度响应功率谱密度Fig.7 Comparison of 4 bushing’ s longitudinal acceleration response PSD under white noise torque excitation |
由于转矩波动主要引起悬架系统的纵向振动, 并且考虑到系统垂向振动传递特性分析与纵向振动传递特性分析存在较多相似, 故不再对垂向振动传递特性作详细分析说明。
本文选取悬架系统的纵向和垂向振动传递特性(即纵向和垂向传递函数)为优化目标, 在保持垂向传递特性的同时着重优化纵向40~200 Hz频率段的振动传递特性。
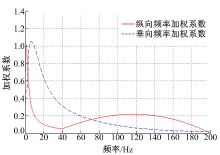
首先, 根据汽车平顺性国标GB/T 13441.1-2007采用“ 1/3倍频程下的基本频率加权方法” , 并在此基础上适当提高了纵向40~200 Hz频率段的加权系数, 对悬架系统的纵向和垂向传递函数进行加权, 如图8所示。然后, 对加权后的传递函数曲线求面积, 得到加权后的传递函数曲线面积SLongitu、SVertical。最后, 得到加权曲线面积的相对变化率Δ Longitu、Δ Vertical:
式中:SVertical, 0和SLongtitu, 0为优化变量取初始值时的加权后曲线面积。
通过寻求加权曲线面积相对变化率的最小值, 便可以得到目标频段最小的传递函数即最优的振动传递特性。因此确定优化目标函数为:
由前文可知, 扭杆梁的各向等效刚度对于悬架系统目标频段内的模态频率分布影响最大, 而纵臂与车身连接处的衬套是转矩波动引起的纵向振动的主要传递路径。因此将扭杆梁和纵臂与车身连接处衬套的等效刚度作为主要的优化对象。
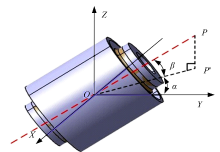
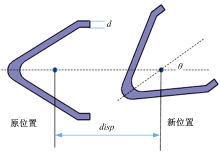
如图9所示, 纵臂与车身连接处的衬套有两个很重要的安装角度α 和β , 即衬套轴线在水平面的投影与Y轴的夹角以及衬套轴线与水平面的夹角。改变这两个安装角度就可以调整衬套X、Y、Z三个方向上的等效刚度。此外, 通过改变扭杆梁的开口角度θ 、位置disp、厚度d可以同时改变扭杆梁弯曲和扭转刚度。因此, 确定扭杆梁的结构调整参数为开口角度θ 、位置disp和厚度d, 如图10所示。优化变量为:
参考文献[13]对于扭杆梁悬架结构优化的案例以及考虑到安装布置的要求, 确定各优化变量的变化范围如表1所示。
| 表1 优化变量初值及范围 Table 1 Initial value and range of optimization variable |
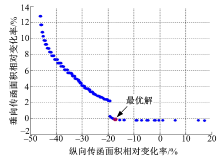
本文利用ISIGHT集成ANSYS、ADAMS和MATLAB, 实现自动优化流程, 并选取NSGA-II作为优化方法, 得到最终的Pareto解集, 如图11所示。由于要保持垂向振动传递特性并使纵向振动传递特性得到最大的优化, 即选取最优解保证Δ Vertical在0以下且Δ Longitu最小, 因此选择如图11所示的点作为最优解。得到优化前、后变量及目标值的比较如表2所示。
由表2可知, 悬架纵向传递函数加权面积下降了17.23%, 而垂向传递函数加权面积也略微下降0.1%, 达到了最初的优化目标。为了更加直观地验证优化效果, 本文取实际驱动电机100 r/min(即车速为10 km/h)时的转矩波动信号作为激励加载在扭杆梁悬架模型上, 得到优化前、后的车身纵向加速度功率谱密度对比如图12所示。
| 表2 优化前、后变量及目标值对比 Table 2 Value comparison of optimization variables and targets |
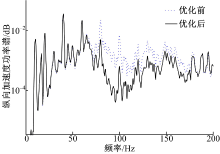 | 图12 优化前后实际转矩作用下车身纵向加速度功率谱对比Fig.12 Comparison of the body’ s longitudinal acceleration PSD before and after optimization |
从图12可以看到, 优化后的悬架系统很好地衰减了车身在65~180 Hz的纵向振动加速度幅值。在当前最优解情况下, 40~65 Hz和180~200 Hz段的优化效果并不明显。而取当前最优解靠左的点作为最优解时, 可以很好地扩大衰减频率范围, 但同时会给垂向振动传递特性带来负面影响, 并不符合本文最初的优化目标(即保持垂向振动传递特性的前提), 故此处只能作一折衷。
(1)实现了一种新型橡胶衬套模型在ADAMS中的仿真调用, 相较于传统衬套模型更能精确反映衬套在高频段的动态力学特性, 有助于提高悬架系统模型高频仿真的精度。此外, 结合扭杆梁柔性化、FTire轮胎模型的应用等措施, 建立了适用于高频仿真的悬架系统模型。
(2)通过振动传递特性分析表明:转矩波动引起的纵向振动主要通过纵臂与车身连接处的衬套传递至车身。
(3)通过合理的优化设计, 在略微减小垂向振动传递函数加权面积的前提下, 使得纵向振动传递函数的加权面积减小17.23%, 并针对实际转矩波动激励在65~180 Hz频段(覆盖绝大部分目标频段)对纵向振动有显著衰减。
(4)利用ISIGHT软件集成ANSYS、ADAMS和MATLAB实现多目标多变量优化, 并为自动实现刚柔耦合模型“ 建模-仿真-优化” 一体化优化方法提供了借鉴。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|