考虑交通量随机波动的随机用户均衡配流模型

引用本文

卫翀, 邵春福. 考虑交通量随机波动的随机用户均衡配流模型. 2015, 45(5): 1408-1413
WEI Chong, SHAO Chun-fu. Stochastic user equilibrium traffic assignment model consisting fluctuations in traffic flows. Journal of Jilin University Engineering and Technology Edition, 2015, 45(5): 1408-1413 复制到剪切板

Permissions

考虑交通量随机波动的随机用户均衡配流模型

卫翀^1,², 邵春福¹

1.北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京 100044

2.首都世界城市顺畅交通协同创新中心,北京 100124

作者简介:卫翀(1981-),男,副教授,博士.研究方向:交通网络建模与分析.E-mail:chwei@bjtu.edu.cn

基金:“973”国家重点基础研究发展计划项目(2012CB725403); 国家自然科学基金项目(51408035); 中央高校基本科研业务费专项项目(2013JBM008)

摘要

研究了随机用户均衡路网中交通量的随机波动现象。基于随机效用理论,运用贝叶斯定理构建了可以反映随机用户均衡路网中路径路段交通量概率分布的交通配流模型,避免了交通量的随机性在交通配流模型中被忽略的问题。侧重分析了路网中驾驶员的随机路径选择行为以及道路通行能力的不确定性对交通量波动的影响。设计了一种马科夫链-蒙特卡洛算法用来根据交通量概率分布估计路径路段交通量的统计特征。在一个中等规模路网上对提案模型进行了验证,结果表明:模型可以有效地评估出路径选择行为以及通行能力不确定性等因素对交通量波动的影响。

关键词: 交通运输系统工程; 随机用户均衡; 交通量概率分布; 贝叶斯定理; 随机效用理论

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2015)05-1408-06

Stochastic user equilibrium traffic assignment model consisting fluctuations in traffic flows

WEI Chong^1,², SHAO Chun-fu¹

1.MOE Key Laboratory for Transportation Complex Systems Theory and Technology, Beijing Jiaotong University, Beijing 100044, China

2.Center of Cooperative Innovation for Beijing Metropolitan Transportation, Beijing 100124, China

Abstract

The stochastic nature of traffic flow in stochastic user equilibrium networks was investigated. Based on the random utility theory, a stochastic traffic assignment model that can reflect the probability distribution of traffic flow was constructed using Baye's theorem. Driver's route choice behavior and the uncertainty in road capacity were taken into account in the model as the sources of fluctuation in traffic flow. A Markov chain Monte Carlo algorithm was also developed in order to estimate the characteristics of traffic flows from the probability distribution. The proposed model was tested on a medium-sized network. Results show that the model can be used to evaluate the effects of route choice behavior and uncertainty in road capacity on the fluctuations in traffic flows.

Keyword: engineering of communication and transportation; stochastic user equilibrium; probability distribution of traffic flows; Baye's theorem; random utility theory

Show Figures

0 引言

路网中交通量的随机波动与路网运营质量紧密相关^[1], 是建立交通配流模型时需要考虑到的一个重要现象。在以往的研究中, 研究者们提出了多种可以在交通配流模型中描述交通量随机波动性的建模方法。例如, Cascetta^[2]以及Watling^[3]提出了基于马科夫链理论的逐日学习型交通配流模型。Asakura等^{[1, 4]}, Shao等^[5]从OD间交通需求随机波动的角度出发讨论了路网中交通量的随机波动性。Hazelton^{[6, 7]}基于Hammersley-Clifford定理构建了一种遵循随机效用理论并可以输出路径路段交通量统计特征的CSUE(Conditional stochastic user equilibrium)模型, 但是该模型并不能给出交通量概率分布的具体形式, 并且该模型的计算量会随交通需求量的增加而增加。Watling^[8]基于渐进均衡条件建立了广义随机用户均衡模型(GSUE)并应用泰勒展开讨论了模型的解法, 但是该模型同样不能明确交通量概率分布的具体形式。Wei等^[9]讨论了均衡网络中交通量概率分布的情况, 但是没有考虑路网属性的不确定性与交通量随机波动性之间的关系。国内也有学者从交通系统演进的角度探讨了交通量的随机特性^{[10, 11]}, 但是这些研究的目的并不在于探索均衡网络中交通量的概率分布。在O-D需求确定的随机用户均衡路网中路径交通量的随机性主要源于驾驶员的随机路径选择行为和路网本身属性的不确定性, 并且交通量实质上是随机变量, 其概率分布的形式应在交通配流模型中得以明确体现。

本文提出了一种基于随机效用理论, 考虑到了随机用户均衡网路中交通量随机波动性的交通配流模型, 并开发算法根据模型反映出的交通量概率分布估计交通量的统计特征。

1 交通量的随机波动性

1.1 通行能力确定的情况

下面将从随机效用理论出发逐步推导出随机用户均衡路网中交通量的概率分布。基于随机效用理论, 可用下式来描述路径选择问题:

$\begin{matrix} \begin{matrix} P (su b_{i} | c_{i}) = P (U_{c_{i}} > U_{h} \forall h, h \neq c_{i}) = \\ P (V_{c_{i}} + ε_{c_{i}} > V_{h} + ε_{h} \forall h, h \neq c_{i}) (1) \end{matrix} \end{matrix}$

式中:P(sub_i|c_i)是一个条件概率, c_i为驾驶员i的路径选择结果, sub_i表示驾驶员i服从随机用户行为(Stochastic user behavior)^[7]。随机用户行为的定义如下:驾驶员选择了一条他或她所感知的效用最大的路径的这样一种行为被称为随机用户行为。应注意式(1)中条件概率的前提条件仅仅表明驾驶员的路径选择结果是c_i; 另一方面sub_i仅仅表示了驾驶员选择路径的行为规则, 但是并没有包含路径选择结果的信息。如式(1)所示, 驾驶员i的路径选择结果是c_i这一条件已给定的前提下sub_i可以被等价地表达为 $\begin{matrix} U_{c_{i}} \end{matrix}$ > U_h∀ h, h≠ c_i, 其中U_h为路径h的随机效用, 随机效用的可观测部分V_h由路径行程时间决定, ε _h为驾驶员对路径行程时间的感知误差。

接下来在交通网络的背景下进一步扩展式(1)。为了方便起见, 用I来表示网络中所有驾驶员集合; 用向量c表示c_j∀ j∈ I, 即网络中所有驾驶员的路径选择结果; 用R表示网络中所有路径的集合; 用向量f表示路径交通量集合。参照式(1), 当所有驾驶员的路径选择结果c为给定条件时, 驾驶员i服从随机用户行为这一事件的概率可以表示为:

$\begin{matrix} \begin{matrix} P (su b_{i} | c) = P (V_{c_{i}} (c) + ε_{c_{i}} > \\ V_{h} (c) + ε_{h} \forall h, h \neq c_{i}) (2) \end{matrix} \end{matrix}$

式中:V_h(c)为根据所有驾驶员的路径选择结果所确定下来的可观测效用。具体来说, V_h(c)包含了下面一系列的关系:由于路径交通量是路径选择结果的叠加, 所以根据c可以计算出路网中的路径交通量f, 并且这个结果是唯一确定的; 根据路径交通量又可以计算出每条路径的行程时间, 路径的行程时间进而又决定了V_h的值。

在随机用户行为的基础上, Hazelton^[7]指出随机用户均衡可以表达为:当路网上所有的驾驶员都服从随机用户行为时, 路网处于随机用户均衡状态。如果用sue来表示路网处于随机用户均衡状态, 那么sue可以等价地表示为sub_i∀ i∈ I。当所有驾驶员的路径选择结果c作为给定条件时, 路网处于用户均衡状态这一事件的概率为:

$\begin{matrix} P (sue | c) = \prod_{\forall i \in I} P (su b_{i} | c) = p {(r | c)}^{f_{r} (c)} (3) \end{matrix}$

式中:f_r(c)为根据所有驾驶员的路径选择结果c所确定的路径r的交通量; p(r|c)为在路径选择结果c作为条件给定的情况下, 路径r的效用为最大这一事件发生的概率。

$\begin{matrix} \begin{matrix} p (r | c) = P (V_{r} (c) + ε_{r} > V_{h} (c) + \\ ε_{h} \forall h, h \neq r) (4) \end{matrix} \end{matrix}$

需要补充说明的是, 式(3)中假设所有驾驶员都是同质的(homogeneous), 也就是说如果c_i=c_m。式(3)所显示的概率实际上是路径选择结果的似然函数, 应用贝叶斯定理可以从似然函数反过来推导出在路网已处于用户均衡状态这一条件给定的情况下路网上驾驶员路径选择结果是c的概率:

$\begin{matrix} P (c | sue) = \frac{P (sue | c) P (c)}{P (sue)} (5) \end{matrix}$

式中:驾驶员的路径选择结果是随机变量, 从贝叶斯统计学的观点来看, P(c)可以被理解为是路径选择结果的先验概率, 这个先验概率是一个均匀分布; P(sue)表示网络处于用户随机均衡的概率, 这一概率的值并不受路径选择结果c的影响。基于以上两点原因, 式(5)可以被改写为:

$\begin{matrix} P (c | sue) \infty P (sue | c) (6) \end{matrix}$

对于一个交通配流问题, 研究的重心在于分析交通量的分布情况, 而不仅仅是掌握所有驾驶员的路径选择行为结果。交通量实质上是驾驶员路径选择结果的叠加, 所以可以通过式(6)推导出网络已处于随机用户均衡状态下路径交通量的概率分布。在开始推导之前, 应该先注意到如果所有驾驶员的路径选择结果c已经给定, 路网中所有路径的交通量可以被唯一确定下来。但是反过来, 如果网络中路径交通量给定, 与之对应的路径选择结果c并不是唯一确定的, 而是有M种可能的情况。M的计算公式为:

$\begin{matrix} M = \sum_{\forall c : f (c) = f} 1 = \prod_{\forall n \in N} \frac{q_{n}!}{\prod_{\forall r \in R_{n}} f_{r}!} (7) \end{matrix}$

式中:f(c)为根据c算出的路径交通量向量; ∀ c:f $\begin{matrix} (c) \end{matrix}$ =f表示所有可以使等式f(c)=f成立的路径选择结果; N为网络中OD对的集合; R_n为第n对OD之间的路径集合; q_n为第n对OD之间的交通需求。

根据式(6)(7), 网络处于随机用户均衡状态下路径交通量为f的概率可以表示为:

$\begin{matrix} \begin{matrix} P (f | sue) = \sum_{\forall c : f (c) = f} P (c | sue) \propto \\ \sum_{\forall c : f (c) = f} P (sue | c) = \\ \sum_{\forall c : f (c) = f} p {(r | c)}^{f_{r} (c)} = \\ \prod_{\forall n \in N} \frac{q_{n}!}{\prod_{\forall r \in R_{n}} f_{r}!} p {(r | f)}^{f_{r}} (8) \end{matrix} \end{matrix}$

式中:

$\begin{matrix} \begin{matrix} p (r | f) = P (V_{r} (f) + ε_{r} > V_{h} (f) + \\ ε_{h} \forall h, h \neq c_{i}) (9) \end{matrix} \end{matrix}$

V_r(f)的可观测效用是由与路径交通量对应的路径行程时间所确定的。

需要指出的是, 式(8)所示的概率模型与Sheffi^[12]提出的多项式概率模型是完全不同的。Sheffi模型中路径行程时间是恒定不变的, 不受路径交通量大小的影响, 所以其模型并非本文所讨论的均衡模型范畴。

1.2 通行能力不确定的情况

式(8)反映了随机路径选择行为与路径交通量随机波动性之间的关系。本文接下来进一步考察路网属性的不确定性对路径交通量随机波动性的影响。这里仅讨论路段通行能力的不确定性这一因素。但是提出的模型具有普遍性, 其他因素可以通过相同的方法来考虑。

用s来表示路段通行能力并且设通行能力服从正态分布。用μ 、σ 分别表示该正态分布的均值和标准差。在交通配流问题中, sue、μ 和σ 被视为给定的条件, 配流结果可以用条件概率P(f|sue, μ , σ )来表述。推导P(f|sue, μ , σ )和推导P(f|sue)的思路类似, 可以从P(sue|c, s)开始讨论。该概率表示如下:

$\begin{matrix} P (sue | c, s) = p {(r | c, s)}^{f_{r} (c)} (10) \end{matrix}$

式中:p(r|c, s)表示在c和s作为给定条件的情况下, 路径r的效用为最大这一事件发生的概率, 其中路径的可观测效用由c和s决定的。

通过P(sue|c, s)可以进一步得到P(f, s|sue, μ , σ ), 有:

$\begin{matrix} \begin{matrix} P (f, s | sue, μ, σ) = \\ \sum_{\forall c : f (c) = c} P (c, s | sue, μ, σ) = \\ \sum_{\forall c : f (c) = c} \frac{P (sue | c, s) P (c) P (s | μ, σ) P (μ, σ)}{P (sue, μ, σ)} \propto \\ \sum_{\forall c : f (c) = c} p {(r | c, s)}^{f_{r} (c)} P (s | μ, σ) = \\ \prod_{\forall n \in N} \frac{q_{n}!}{\prod_{\forall r \in R_{n}} f_{r}!} p {(r | f, s)}^{f_{r}} P (s | μ, σ) (11) \end{matrix} \end{matrix}$

式中:P(μ , σ )和P(sue, μ , σ )为常数, 因为这些概率的值都不受f和s影响; P(sue|c, s)已经由式(10)给出; p(r|f, s)表示在f和s作为条件给定的情况下, 路径r的效用为最大这一事件发生的概率; P(s|μ , σ )表示给定均值和标准差的情况下路段通行能力为s的概率。

由P(f, s|sue, μ , σ )可以最终推导出当sue、μ 和σ 为给定条件时, 路网中路径交通量为f的概率:

$\begin{matrix} \begin{matrix} P (f | sue, μ, σ) = \\ \int_{s} P (f, s | sue, μ, σ) ds \propto \\ \int_{s} \prod_{\forall n \in N} \frac{q_{n}!}{\prod_{\forall r \in R_{n}} f_{r}!} p {(r | f, s)}^{f_{r}} P (s | μ, σ) ds (12) \end{matrix} \end{matrix}$

式(12)给出了路径交通量f所对应概率密度函数的一般形式, 概率密度函数的具体表达将随着与p(r|f, s)相对应的路径选择模型的不同而变化。通过概率密度函数的表达式实际上并不能直观地反映出路径路段交通量的均值和方差等特征, 因此本文将通过马科夫链-蒙特卡洛(Markov chain Monte Carlo)算法来根据推导出的概率密度函数估计出交通量的均值和方差等特征。

2 交通量的统计特征

根据已知概率密度函数可以计算随机变量的统计特征。式(12)反映了路径交通量这一随机变量所对应的概率密度函数。虽然该概率密度函数的形式较为复杂, 但可用马科夫链-蒙特卡洛算法^{[13, 14]}来估计交通量的统计特征值。马科夫链-蒙特卡洛算法的数学基础是马科夫过程, Andrieu等^[15]详细介绍了该算法的基本原理。应用该算法可以产生一系列来自概率分布P(f|sue, μ , σ )的随机样本。通过汇总这些随机样本便可以得到f的统计特征值。然而, 马科夫链-蒙特卡洛算法在运行过程中需要计算式(12)所示的概率密度函数, 因此会产生频繁的积分计算。本文通过将数据扩张技术(Data augmentation)与马科夫链-蒙特卡洛算法结合使用来避免积分计算。所设计的算法并不直接从概率分布P(f|sue, μ , σ )中抽取f的随机样本, 而是从式(11)所示的联合概率分布P(f, s|sue, μ , σ )中抽取f和s的随机样本, 然后用抽出的f的随机样本来估计出路径交通量的均值和方差等统计特征。

以下用f^t和s^t表示从P(f, s|sue, μ , σ )中抽取的第t个样本。用马科夫链-蒙特卡洛算法抽出f^t和s^t的过程可简要概括如下:

步骤1 抽出一个随机数f^*, 再从多维正态分布中抽取一个随机样本s^*, 该多维正态分布均值为s^t-¹, 协方差矩阵是一个维数与s^t-¹相对应的单位矩阵。

步骤2 计算

$\begin{matrix} τ = \frac{P (f^{*}, s^{*} | sue, μ, σ) P (f^{t - 1} | f^{*})}{P (f^{t - 1}, s^{t - 1} | sue, μ, σ) P (f^{*} | f^{t - 1})} (13) \end{matrix}$

步骤3 以min(1, τ )的概率接受f^*, s^*为抽取的第t个样本, 即以min(1, τ )的概率设f^t=f^*, s^t=s^*, 以1-min(1, τ )的概率设f^t=f^t-¹, s^t=s^t-¹。

在抽出第一个样本f^t、s^t之前需要设定一个初始值f⁰、s⁰, 这个初始值并不影响抽样过程, 可以任意设定。在上述算法中f^*是来自一个多项式概率分布的随机样本。该分布的参数由f^t-¹决定, 其概率密度函数为:

$\begin{matrix} P (f^{*} | f^{t - 1}) = \prod_{\forall n \in N} \frac{q_{n}!}{\prod_{\forall r \in R_{n}} f_{r}^{*}!} {(\frac{f_{r}^{t - 1}}{q_{n}})}^{f_{r}^{*}} (14) \end{matrix}$

算法中P(f^t-¹|f^*)的值可通过交换式(14)中f^t-¹和f^*的位置后进行计算。

重复上述步骤t次后产生的结果f¹, s¹, f², s², …, f^t, s^t是从式(11)所对应的概率分布中抽取出的一组随机样本。

3 数值计算示例

本文用文献[9]中的含有13个节点的路网测试了提出的交通配流模型。路网中有3对O-D对, 分别是点1到点2, 点1到点3, 和点4到点2。三对O-D对之间的交通需求分别是50, 30和30。本文中用下面的Logit模型来计算p(r|f, s)的值并用β 表示Logit模型的参数。在实际应用中β 也可被设置为随机变量^[16]。

令β =0.35, μ =40, σ =5。应用前文描述的马科夫链-蒙特卡洛算法, 从概率分布P(f, s|sue, μ , σ )中抽取一系列路径交通量f的随机样本。图1和图2用抽出的随机样本的直方图展示了通过节点1, 12, 8, 2的路径和通过节点4, 5, 9, 10, 11, 2的路径所承担交通量的概率分布情况。从这些输出结果可以看出:提案交通配流模型可以完整地描述路网中交通量的随机波动性, 而不是像传统的配流模型那样仅输出交通量的均值。基于马科夫链-蒙特卡洛算法抽取的随机样本还可以进一步估计出交通量的统计特征, 其中交通量的方差具体反映了交通量的随机波动性。

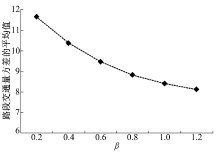
模型参数β 和σ 实际上分别反映了路径选择行为的随机性和路网属性的不确定性。其中β 为路径选择模型的参数, 该参数的取值越大, 表明驾驶员对路径行程时间的感知误差越小, 即路径选择的随机性越小。又由于路径选择结果与交通量之间存在叠加关系, 所以β 的值对交通量的方差是有影响的。为了考察这一点, 设μ =40, σ =5, 分别计算了β 等于0.2, 0.4, 0.6, 0.8, 1和1.2时路网中路段交通量方差的平均值。各个路段交通量的方差可以用马科夫链-蒙特卡洛算法所抽取的随机样本来计算。图3显示了计算结果。从图中可以看到:随着β 取值的增大, 或者说随着驾驶员对路径行程时间的感知误差的减小, 路段交通量方差的平均值将逐渐减小。

在交通配流模型中σ 表示路段的通行能力。σ 变大会使路径行程时间的不确定性变大, 与之相关联的驾驶员路径选择结果的随机性也会随之加大。

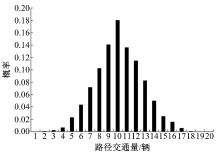	Figure Option View Download New Window
	图1 经过点1-12-8-2的路径所承担交通量的随机样本直方图Fig.1 Histogram of simulated samples for the route that visits node 1-12-8-2

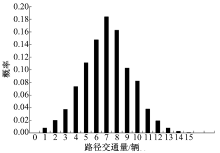	Figure Option View Download New Window
	图2 经过点4-5-9-10-11-2的路径所承担交通量的随机样本的直方图Fig.2 Histogram of simulated samples for the route that visits node 4-5-9-10-11-2

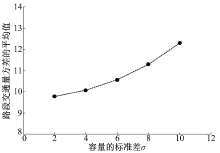
	Figure Option View Download New Window
	图3 β 的取值对路段交通量方差的影响Fig.3 Effect of β on the variances of link traffic flows

为了考察σ 的取值对路段交通量随机波动性的影响, 设β =0.35, μ =40, 分别计算了σ 等于2, 4, 6, 8和10时路网中路段交通量方差的平均值。图4为计算结果。从图中可以看出:随着通行能力不确定性的增大, 路段交通量方差的平均值也随之增大。从σ 对路径选择结果的影响以及路径选择结果与交通量的关系可以看出, 这种交通量方差逐渐增大现象本质上是由于路径选择结果的不确定性相应变大引起的。

	Figure Option View Download New Window
	图4 σ 的取值对路段交通量方差的影响Fig.4 Effect of σ on the variances of link traffic flows

4 结束语

在处于随机用户均衡的道路网中, 路径交通量是随机波动的, 其所对应的概率分布可以运用贝叶斯定理根据随机效用理论推导出来。基于马科夫链-蒙特卡洛算法可以进一步计算出随机用户均衡网络中路径路段交通量的均值和方差等统计特征值。研究结果表明:驾驶员的路径选择行为以及道路通行能力的不确定性均会影响到交通量的随机波动特性, 这种影响在路径交通量的概率密度函数中有明确的体现。数值计算结果显示, 当驾驶员对行程时间的感知误差较大时或道路通行能力的不确定性较高时都会使得路径路段交通量的方差变大。基于随机效用理论所建立的随机用户均衡配流模型可以描述出交通量的随机波动性, 为交通网络可靠性分析提供必要的信息。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Asakura Y, Kashiwadani M. Road network reliability caused by daily fluctuation of traffic flow[C]∥Proceedings of the 19th PTRC Summer Annual Meeting, Brighton UK, 1991: 73-84. [本文引用:2]
[2]	Cascetta E. A stochastic process approach to the analysis of temporal dynamics in transportation networks[J]. Transportation Research Part B, 1989, 23(1): 1-17. [本文引用:1]
[3]	Watling D. Asymmetric problems and stochastic process models of traffic assignment[J]. Transportation Research Part B, 1996, 30(5): 339-357. [本文引用:1]
[4]	Asakura Y. Reliability measures of an origin and destination pair in a deteriorated road network with variable flows[C]∥Proceedings of the 4th Meeting of the EURO Working Group in Transportation, Newcastle UK, 1996: 273-288. [本文引用:1]
[5]	Shao H, Lam W H K, Tam M L. A reliability-based stochastic traffic assignment model for network with multiple user classes under uncertainty in demand [J]. Networks and Spatial Economics, 2006, 6(3/4): 173-204. [本文引用:1]
[6]	Hazelton M L, Lee S, Polak J W. Stationary states in stochastic process models of traffic assignment: a Markov chain Monte Carlo approach[C]∥Proceedings of the 13th International Symposium on Transportation and Traffic Theory, Lyon, France, 1996: 341-357. [本文引用:1]
[7]	Hazelton M L. Some remarks on stochastic user equilibrium[J]. Transportation Research Part B, 1998, 32(2): 101-108. [本文引用:3]
[8]	Watling D P. A second order stochastic network equilibrium model. I: theoretical foundation: a second order stochastic network equilibrium model. II: solution method and numerical experiments[J]. Transportation Science, 2002, 36(2): 149-183. [本文引用:1]
[9]	Wei C, Asakura Y, Iryo Y. The posterior probability distribution of traffic flow: a new scheme for the assignment of stochastic traffic flow[J]. Tranportmetrica A: Transport Science, 2013, 9(8): 753-771. [本文引用:1]
[10]	刘天亮, 黄海军. 日常择路行为的多智能体模拟[J]. 物理学报, 2007, 56(11): 6321-6325. Liu Tian-liang, Huang Hai-jun. Multi-agent simulation on day-to-day route choice behavior[J]. Acta Physica Sinica, 2007, 56(11): 6321-6325. [本文引用:1]
[11]	刘诗序, 关宏志, 严海. 预测信息下的驾驶员逐日路径选择行为与系统演化[J]. 北京工业大学学报, 2012, 38(2): 269-274. Liu Shi-xu, Guan Hong-zhi, Yan Hai. Drivers'day-to-day route choice behavior and system evolution under forecast information[J]. Journal of Beijing University of Technology, 2012, 38(2): 269-274. [本文引用:1]
[12]	Sheffi Y. Urban Transportation Networks: Equilibrium Analysis with Mathematical Programming Methods[M]. Englewood Cliffs, NJ: Prentice-Hall, 1985. [本文引用:1]
[13]	Metropolis N, Rosenbluth A W, Rosenbluth M N. Equations of state calculations by fast computing machines[J]. Journal of Chemical Physics, 1953, 21(6): 1087-1091. [本文引用:1]
[14]	Hastings W K. Monte Carlo sampling methods using Markov chains and their applications[J]. Biometrika, 1970, 57(1): 97-109. [本文引用:1]
[15]	Andrieu C, de Freitas N, Doucet A, et al. An introduction to MCMC for machine learning[J]. Machine Learning, 2003, 50(1): 5-43. [本文引用:1]
[16]	罗清玉, 孙宝凤, 吴文静, 等. 基于Mixed logit模型的拥挤收费下交通方式分担率预测[J]. 吉林大学学报: 工学版, 2010, 40(5): 1230-1234. Luo Qing-yu, Sun Bao-feng, Wu Wen-jing, et al. Predicting traffic mode split under congestion pricing based on mixed logit model[J]. Journal of Jilin University (Engineering and Technology Edition), 2010, 40(5): 1230-1234. [本文引用:1]

1991

0.0

... 0 引言路网中交通量的随机波动与路网运营质量紧密相关^[1],是建立交通配流模型时需要考虑到的一个重要现象 ...

... Asakura等^[1,4],Shao等^[5]从OD间交通需求随机波动的角度出发讨论了路网中交通量的随机波动性 ...

1989

0.0

... 例如,Cascetta^[2]以及Watling^[3]提出了基于马科夫链理论的逐日学习型交通配流模型 ...

1996

0.0

... 例如,Cascetta^[2]以及Watling^[3]提出了基于马科夫链理论的逐日学习型交通配流模型 ...

1996

0.0

... Asakura等^[1,4],Shao等^[5]从OD间交通需求随机波动的角度出发讨论了路网中交通量的随机波动性 ...

2006

0.0

... Asakura等^[1,4],Shao等^[5]从OD间交通需求随机波动的角度出发讨论了路网中交通量的随机波动性 ...

1996

0.0

... Hazelton^[6,7]基于Hammersley-Clifford定理构建了一种遵循随机效用理论并可以输出路径路段交通量统计特征的CSUE(Conditional stochastic user equilibrium)模型,但是该模型并不能给出交通量概率分布的具体形式,并且该模型的计算量会随交通需求量的增加而增加 ...

1998

0.0

... 式中:P(sub_i|c_i)是一个条件概率,c_i为驾驶员i的路径选择结果,sub_i表示驾驶员i服从随机用户行为(Stochastic user behavior)^[7] ...

... 在随机用户行为的基础上,Hazelton^[7]指出随机用户均衡可以表达为:当路网上所有的驾驶员都服从随机用户行为时,路网处于随机用户均衡状态 ...

2002

0.0

... Watling^[8]基于渐进均衡条件建立了广义随机用户均衡模型(GSUE)并应用泰勒展开讨论了模型的解法,但是该模型同样不能明确交通量概率分布的具体形式 ...

2013

0.0

... Wei等^[9]讨论了均衡网络中交通量概率分布的情况,但是没有考虑路网属性的不确定性与交通量随机波动性之间的关系 ...

2007

0.0

. 2007, 56(11):6321-6325 DOI:doi:10.3321/j.issn:1000-3290.2007.11.027

Multi-agent simulation on day-to-day route choice behavior

日常择路行为的多智能体模拟

Liu Tian-liang , Huang Hai-jun.

刘天亮, 黄海军

The day-to-day route choice is a non-cooperative game process with many participants during a long time period. We use the multi-agent simulation system SeSAm to investigate two different route update rules designed for traffic information release and unrelease respectively. Simulation results on a small grid network show that the rule under information release can make route flow evolve to the logit stochastic user equilibrium faster than that under information unrelease. However, the flow pattern may be unstable if travelers put undue compliance on the released information. A stable flow pattern can also be achieved only relying on travelers' perceived experience and learning ability, but the evolution is rather slow. It is thus suggested that the traffic information should be timely released to public meanwhile utilized properly.

日常路径选择是一个长期的、多体参与的非合作博弈过程.基于多智能体环境，对交通信息公开和不公开两种路径更新规则进行了模拟研究，结果表明，信息公开比不公开能够使路径流量更快地演化到logit随机用户均衡状态，但若对信息的依赖程度过大，则可能导致系统振荡；出行者完全依靠自身经验完成路径选择也可以使系统演化至稳定态，但代价是演化效率太低.因此，既要公开交通信息，又要注意合理使用信息.

... 国内也有学者从交通系统演进的角度探讨了交通量的随机特性^[10,11],但是这些研究的目的并不在于探索均衡网络中交通量的概率分布 ...

2012

0.0

. 2012, 38(2):269-274

Drivers'day-to-day route choice behavior and system evolution under forecast information

预测信息下的驾驶员逐日路径选择行为与系统演化

Liu Shi-xu , Guan Hong-zhi , Yan Hai.

刘诗序, 关宏志, 严海

运用微观仿真方法,研究预测信息作用下驾驶员逐日路径选择行为与路网交通流的演化.首先,分析了目前研究存在的不足,针对预测信息情形,设计了一种可行的行程时间预测方法,根据驾驶员逐日路径选择过程,建立了理解行程时间更新模型和路径选择模型.然后,在2条平行路径的简单路网中,仿真了预测信息条件下驾驶员逐日路径选择过程,分析了模型参数取值不同时路径流量随时间演化的波动性和路网系统的效率.结果表明：路网流量的波动性和系统效率都与驾驶员对预测信息的依赖程度和预测模型参数有关,且二者的变化规律相似.最后,以系统最优为目标,给出了预测模型参数的最佳取值范围.

... 国内也有学者从交通系统演进的角度探讨了交通量的随机特性^[10,11],但是这些研究的目的并不在于探索均衡网络中交通量的概率分布 ...

1985

0.0

... 需要指出的是,式(8)所示的概率模型与Sheffi^[12]提出的多项式概率模型是完全不同的 ...

1953

0.0

... 虽然该概率密度函数的形式较为复杂,但可用马科夫链-蒙特卡洛算法^[13,14]来估计交通量的统计特征值 ...

1970

0.0

... 虽然该概率密度函数的形式较为复杂,但可用马科夫链-蒙特卡洛算法^[13,14]来估计交通量的统计特征值 ...

2003

0.0

... 马科夫链-蒙特卡洛算法的数学基础是马科夫过程,Andrieu等^[15]详细介绍了该算法的基本原理 ...

2010

0.0

. 2010, 40(5):1230-1234

Predicting traffic mode split under congestion pricing based on mixed logit model

基于Mixed logit模型的拥挤收费下交通方式分担率预测

Luo Qing-yu , Sun Bao-feng , Wu Wen-jing

罗清玉, 孙宝凤, 吴文静

The drawbacks of the traditional disaggregate models were analyzed and a new idea to investigate the traffic mode split under congestion pricing was proposed based on the mixed logit model. A traffic mode selection model was built based on the mixed logit model and the real inhabitant travel behavior data. The model was calibrated and simulated by the software SAS, including the Monte Carlo simulation. It was proved that the model is accurate and serviceable. The change of the traffic mode split under different congestion pricing rate can be predicted by the sensitivity analysis with the introduction of congestion pricing. The suggested model provides an approach to the analysis of travel behavior and the study of traffic impacts under the policy of congestion pricing, as well as the evaluation of other policies for travel demand management.

分析了传统非集计模型存在的缺陷，提出利用mixed logit模型研究拥挤收费下交通方式分担率变化的思路。结合实际居民出行数据建立了基于mixed logit的交通方式选择模型，利用SAS软件进行蒙特卡罗模拟计算，标定了模型并进行了仿真分析。经验证，所建模型具有较高的命中率和可用性。加入拥挤收费影响因素进行敏感性分析，可得出不同拥挤收费费率下的交通方式分担率。应用该模型能为拥挤收费下的出行行为分析和交通影响研究以及其他交通需求管理政策的评价提供了方法。

... 也可被设置为随机变量^[16] ...