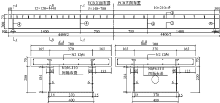
共设计6片直线简支箱型试验梁, 箱型截面。考虑试验场地和加载条件, 最终确定试验梁主要尺寸为:跨度4200 mm, 梁全长4500 mm; 混凝土板宽700 mm, 厚70 mm; 钢梁高200 mm, 下翼缘宽400 mm, 各上翼缘宽60 mm, 上、下翼缘板厚8 mm, 腹板厚6 mm。结合梁全高270 mm, 高跨比约为1/16, 高宽比为1/6。栓钉采用威迪建筑钢品有限公司生产的标准栓钉, 直径13 mm, 高50 mm。试验梁的横截面及立面布置图见图1。

6片试验梁中, 其中3片为完全连接的结合梁(FCB系列), 沿截面横向在每个腹板上方布置一列栓钉, 沿梁轴纵向各排栓钉间距在剪跨区为120 mm, 在无剪力区为140 mm, 每片梁共布置栓钉70个; 另外3片为部分连接的结合梁(PCB系列), 沿截面横向在每个腹板上方布置一列栓钉, 沿梁轴纵向各排栓钉间距(在整个梁跨均匀布置)为210 mm, 每片梁共布置栓钉42个, 剪力连接度为60%。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 结合梁立面及横截面图(单位:mm)Fig.1 Elevation view and cross-section of the model composite beams(unit:mm)

采集设备为北京东方振动和噪声技术研究所3018C采集仪和DASP(V10)信号分析软件, 相应的放大器两台, 及相应的供电设备。传感器为941B, 见图2和图3。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 数据采集设备Fig.2 Data acquisition devices

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 941B加速度/速度传感器Fig.3 941B LDVT sensors

加载设备采用甘肃天水红山试验机有限公司生产的1000 kN三维多点协调电液伺服动态加载机, 如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 动态试验机及控制系统Fig.4 Dynamic tester and control system

采用1∶ 10的C70货车模型的参数作为移动荷载模型货车的基本参数, 见表1, 模型的照片见图5。

表1

Table 1

表1(Table 1)

表1 货车模型主要参数 Table 1 Main parameters of the model freight carriage 参 数 数值 说 明 自重/kg 62 包含车轮 轴距/mm 183 轮对中心距离 转向架间距/mm 935 转向架中心间距

表1 货车模型主要参数 Table 1 Main parameters of the model freight carriage

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 货车模型Fig.5 Photograph of the model freight carriage

专门制作了1∶ 10轨道模型, 为模型车辆的运行提供足够的加速、运行及制动的空间, 以模拟车辆通过结合梁的整个过程, 以及测试结合梁产生的动力响应。试验平台的现场布置见图6。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 试验平台现场布置图Fig.6 Site layout of the test platform

轨道、轨枕以及道床整体设计, 每件长2 m, 共8件, 总长共16 m, 其中梁前加速段和梁后减速段各5.8 m, 梁上4.4 m。加速段以及制动段平台以40 mm× 40 mm× 3.5 mm角钢焊成, 并加以护栏。平台上铺设厚木板, 并以螺栓与角钢平台及模型梁固定在一起, 保证轨道的平稳性。

为了给模型车辆提供足够的梁上运行速度, 并在通过桥梁后能够及时制动, 需要制订加速方案以及相应的制动方案。考虑到本试验的车重最大达150 kg, 制动时不仅需要人工减速, 同时也需要设置一定的缓冲以保证安全。

(1)加速方案

根据测试方案的需要, 在6 m加速段采用双人两侧同步推动小车加速, 以保证车辆的平稳运动, 同时做好防护。当车辆第一个轮对运行到梁上时, 停止人工干预, 并跟进对车辆进行防护。

(2)测试段

在梁侧面用标记笔做好明显距离标记, 并摆放好试验工况标签。试验开始后测试人员站在梁跨中侧面一定距离外录像, 记录下小车通过梁的整个过程, 其他人员做好防护。

(3)制动方案

当小车最后一个轮对完全通过梁后, 采用双侧人工同步制动的方法, 以防止车辆偏离轨道或掉落。支架末端布置好缓冲物, 做到双重防护。

(1)跨中响应测试

梁布置在钢支座上, 一端竖向约束, 可自由转动, 另一端竖向约束, 允许一定范围内的纵向位移。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 梁跨中响应测试测点布置示意图Fig.7 Responses measuring point arrangement at midspan

在混凝土板上跨中位置共布置3个竖向传感器, 分别测试结合梁跨中的竖向加速度、速度。传感器布置示意图见图7, 左侧为加速度传感器, 右边两个为速度传感器(其中一个为备用)。

(2)竖向跨中挠度和梁端相对滑移测试

在钢梁跨中底部中心布置竖向动态挠度传感器, 与混凝土板的加速度和速度传感器相配合, 测试模型车辆通过结合梁时的跨中挠度时程。传感器布置方案见图8。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 梁底挠度测点布置示意图Fig.8 Displacement measuring point arrangement at midspan

为研究钢梁与混凝土板在移动荷载作用下的相对滑移规律, 把磁性表座吸附在钢梁底板位置处, 而把位移传感器的探针顶在混凝土板梁端处, 这样位移传感器所测得的数值就是钢梁与混凝土板的相对滑移, 见图9。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 梁端滑移测点布置示意图Fig.9 Slip measuring point arrangement at beam end

考虑到试验条件, 采取录像和波形相结合的方式确定车辆通过桥梁时的平均速度。对于本次试验, 加速和制动段的支架和梁是断开的, 从车辆过桥时的波形来看, 当车辆第一个轮对一上桥, 梁跨中波形挠度立刻增大; 当车辆最后一个轮对出桥时, 由于梁体刚度较大, 其挠度很快变为初始值。车辆通过测试段时, 没有人工干预, 可认为其速度是一个均匀变化的过程, 故从波形可以判断车辆通过的时间。因此, 知道测试段长度、车辆轴距及通过时间, 辅以录像, 就可以计算出车辆通过测试段的平均速度。车辆速度从最低到最高分为5~9个速度等级。

对6片梁均进行了移动荷载作用下梁的动力响应测试, 测试了不同重量的移动荷载以不同速度过梁时结合梁中的动力响应。货车自重为62 kg, 改变车重的方法是加不同的配重, 均匀布置于货车车厢内, 使货车的总质量分别达到100 kg(配重38 kg)和150 kg(配重88 kg)。

以FCB梁、车重为62 kg时例说明测试的过程。当小车以约为2 m/s的速度通过时典型的波形见图10。

图中自上向下依次为跨中竖向速度、加速度和动挠度。由于受到轨道不平顺等因素的干扰, 图中动挠度波形有较大的高频噪声, 未进行滤波。从图中可以看出, 此时跨中最大挠度约为0.07 mm。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 货车重62kg, 车辆通过FCB梁跨中时的某次响应Fig.10 Dynamic response of 62 kg freight carriage passing the midspan of FCB

对于等截面简支直线结合梁, 可得到振型表达式为φ _n(x)=sinλ ₃x=sin(nπ x/L), 那么结合梁振动方程的圆频率为(详细推导见文献[10]):

ωn2=γn2(nπ4(EI)Fm-L41γn2=1+β+(nπ2α(1+β)1+(nπ2α2

式中:α = (EI)CKSh2L2; β = (EI)C(EI)B, (EI)_B=E₁I₁+E₂I₂, 表示混凝土板与钢梁绕自身中性轴的抗弯刚度和; (EI)_C=E₁A₁ h12+E₂A₂ h22, 表示混凝土板与钢梁绕整个梁的中性轴的抗弯刚度和; (EI)_F=(EI)_C+(EI)_B, 表示不考虑滑移时结合梁的截面刚度。

对于单一材料的普通梁(如混凝土梁、钢梁), 相当于K_S趋向于无穷大, 那么α 趋向于零, 从而 γn2趋向于1, 则:

ωn, F=(nπ2L2(EI)Fm-3

形式上与普通直梁一致, 而(EI)_F可视为不考虑抗剪连接件刚度时结合梁的刚度。那么简支结合梁的等效动刚度可表达为:

(EI)eq=γn2(EI)F4

从前文的分析可知, 与普通梁相比, 考虑柔性的抗剪连接件引起滑移后, 结合梁无论是梁的静刚度还是动刚度均有一定的降低。若采用结合梁静力计算中类似的表示方式, γn2可视为简支结合梁第n阶的“ 动力刚度折减系数” , 而γ _n可视为第n阶的“ 频率折减系数” 。因此, 在进行结合梁的静力计算时, 必须要考虑由这种滑移带来的刚度降低^[11]。

根据Duhamel积分求得各阶响应后并求和, 可得到荷载通过梁时的最终反应。若梁的初始条件为零, 即q(0)和 q·(0)均为零, 那么移动力作用下简支结合梁的振动位移特解的表达式为(详细推导见文献[12]):

v(x, t)=∑n=1∞qn(t)·φn(x)=2m∑n=1∞(EI)Bα1+nπ2α1ωD, nsinnπxL×∫0tP(t)sinnπVtLe-ξnωn(t-τ)sinωD, n(t-τ)dτ5

式中:m= m-L为梁的总质量; ω _{D, n}为梁的有阻尼频率; ξ _n为相应的阻尼比。

需要注意的是, 与普通简支梁相比, 上述结果第二项多了一个系数。多个移动力以不同的速度通过梁的响应可用类似方法得到, 此处不再赘述。从形式上看, 式(5)与普通梁的反应并无多大区别, 但与普通梁相比, 各阶自振圆频率的表达式却有显著区别, 并不是一个简单的表达式, 参见式(1)。

将模型参数代入式(1), 得到PCB和FCB梁考虑滑移和不考虑滑移(此时相当于交界面上的抗剪刚度K_S为无穷大, 与普通梁相同)的一阶竖向自振频率的理论值, 见表2。表中同时给出了各试验梁一阶竖向自振频率的理论值、ANSYS有限元计算值和实测值(详细测试过程见文献[13])的结果对比, 其中K_S为单位长度抗剪连接件的纵向剪切刚度值, 当不考虑界面滑移时, K_S=¥ 。栓钉本构模型及相关参数的取值原则参考文献[14]。

表2

Table 2

表2(Table 2)

表2 FCB和PCB模型竖向自振频率结果对比 Table 2 Comparison of the vertical natural frequencies between FCB and PCB Hz 模型 理论计算值 γ12 数值结果 实测 结果 KS /MPa 考虑 滑移 不考虑 滑移 考虑 滑移 不考虑 滑移 FCB 305.32 22.546 28.91 0.608 25.93 31.607 23.13 PCB 183.19 20.921 28.91 0.517 24.11 31.208 21.16

表2 FCB和PCB模型竖向自振频率结果对比 Table 2 Comparison of the vertical natural frequencies between FCB and PCB Hz

从表2可以看出:①考虑界面滑移的理论计算值与实际测试结果非常接近, 说明本文在考虑滑移后的自振特性公式推导是正确的, 如果不考虑滑移, 会比实测结果大36.6%之多。②计算结果和实测结果均表明, 结合梁一阶竖向自振频率随抗剪连接度的减小而减小, 说明结合面滑移使结合梁刚度下降。

求得结合梁自振圆频率具体结果后, 式(5)可直接使用Newmark-β 法进行数值求解。本文采用VBA(Visual basic for applications)进行编程, 并与Microsoft Excel结合进行数值求解。通过调用Excel单元格计算得到的结合梁基本参数, 以VBA编程, 调用上述计算结果, 使用Newmark-β 法对移动荷载列作用下的结合梁响应进行计算。

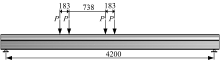
以62 kg的小车以不同速度通过FCB梁和PCB梁时为例, 把模型车辆简化为移动荷载列(荷载图示见图11), 假设阻尼比为0.02, 计算了移动荷载作用下简支结合梁的跨中动力响应。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 小车荷载列分布图示(单位:mm)Fig.11 Load series distribution of the model vehicle

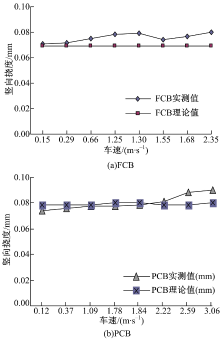
把不同车速作用下FCB和PCB梁的跨中竖向挠度的计算结果和实测结果进行对比, 结果见表3。

从表3可以看出:在62 kg移动荷载作用下, 结合梁的跨中挠度的理论值和实测值吻合良好, 大部分的误差均在5%以下, 验证了本文的结合梁动力理论和试验分析方法是正确的。

表3

Table 3

表3(Table 3)

表3 移动荷载作用下各试验工况的跨中竖向响应 Table 3 Vertical displacement of the beams under moving loads at the midspan 模型梁 车速/ (m· s-1) 跨中最大挠度 动力系数 实测值 /mm 计算值 /mm 误差 /% 实测值 计算值 FCB 0.154 0.071 0.069 2.82 1.255 1.339 0.292 0.072 0.069 4.17 1.273 1.339 0.659 0.075 0.069 8.00 1.325 1.339 1.249 0.078 0.069 11.54 1.379 1.342 1.300 0.079 0.069 12.66 1.397 1.342 1.547 0.074 0.069 6.76 1.308 1.339 1.675 0.077 0.069 10.39 1.362 1.341 2.354 0.080 0.069 13.75 1.414 1.336 PCB 0.124 0.074 0.079 6.76 1.305 1.501 0.366 0.076 0.079 3.95 1.340 1.503 1.093 0.078 0.079 1.28 1.375 1.501 1.783 0.078 0.080 2.56 1.375 1.509 1.836 0.079 0.080 1.27 1.394 1.504 2.219 0.081 0.079 2.47 1.429 1.506 2.588 0.088 0.079 10.23 1.552 1.509 3.062 0.090 0.080 11.11 1.587 1.507

表3 移动荷载作用下各试验工况的跨中竖向响应 Table 3 Vertical displacement of the beams under moving loads at the midspan

图12给出了62 kg小车不同车速下FCB和PCB梁的跨中竖向挠度最大值的计算结果和实测结果的对比。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 FCB和PCB跨中挠度的比较Fig.12 Comparison of the midspan displacement vs speed

为了更清楚地展示车速及连接刚度对结合梁跨中挠度的影响, 图13给出了62 kg的模型小车以10 m/s通过时FCB和PCB梁的跨中竖向挠度时程的计算值, 其中CB表示不考虑滑移时的情况, 相当于单一材料的普通梁(如钢梁、混凝土梁等)。

图13

Fig.13

	Figure Option ViewDownloadNew Window
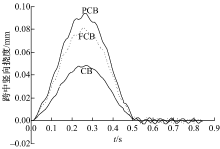	图13 模型车辆作用下结合梁的跨中挠度时程Fig.13 Time history of the midspan displacement of the composite beam under model vehicle

由图12、图13可知:在同样的车重和车速的移动荷载作用下, 部分连接的结合梁跨中会产生更大的动挠度; 由于试验条件所限, 小车的速度远低于共振车速, 因此在实测的速度范围内, 结合梁跨中挠度随车速的增加并不明显。