平衡式两排轴向柱塞泵缸体倾覆力矩

引用本文

邓海顺, 黄坤, 王传礼, 李永梅. 平衡式两排轴向柱塞泵缸体倾覆力矩. 2015, 45(5): 1468-1473
DENG Hai-shun, HUANG Kun, WANG Chuan-li, LI Yong-mei. Overturning moment of cylinder of balanced two-ring axial piston pump. Journal of Jilin University Engineering and Technology Edition, 2015, 45(5): 1468-1473 复制到剪切板

Permissions

平衡式两排轴向柱塞泵缸体倾覆力矩

邓海顺, 黄坤, 王传礼, 李永梅

安徽理工大学机械工程学院, 安徽淮南 232001

王传礼(1964-),男,教授,博士.研究方向:液压传动与控制.E-mail:chlwang@aust.edu.cn

作者简介:邓海顺(1978-),男,副教授,博士.研究方向:液压传动与控制.E-mail:hsdeng@aust.edu.cn

基金:国家自然科学基金项目(51205002,51075001); 安徽省自然科学基金项目(1508085ME80)

摘要

分析了平衡式两排轴向柱塞泵缸体的受力情况,推导了缸体倾覆力矩的计算公式,同时也给出了使缸体、配流盘保持轴向液压力平衡的计算公式和计算程序。取内、外排柱塞同为相等偶数和同为相等奇数,利用Matlab编程绘制出其倾覆力矩随缸体转角变化的动态曲线。研究表明:内、外排柱塞同为相等奇数或偶数时,平衡式两排轴向柱塞泵内外排的倾覆力矩可部分抵消,甚至完全抵消,使其缸体总的倾覆力矩大幅降低,其倾覆力矩的波动周期不变,且内、外排柱塞同为奇数时的倾覆力矩要小于同为偶数时的倾覆力矩。

关键词: 流体传动与控制; 平衡式双排轴向柱塞泵; 缸体; 平衡性; 倾覆力矩

中图分类号:TH322 文献标志码:A 文章编号:1671-5497(2015)05-1468-06

Overturning moment of cylinder of balanced two-ring axial piston pump

DENG Hai-shun, HUANG Kun, WANG Chuan-li, LI Yong-mei

Department of Mechanical Engineering, Anhui University of Science and Technology, Huainan 232001, China

Abstract

The cylinder stress state of the balanced two-ring axial piston pump is analyzed, and a calculation formula of the overturning moment of the cylinder is deduced. Also the calculation formula to balance the axial hydraulic pressure of the cylinder and the port plate is obtained and program is given. When the numbers of the pistons inside and outside are both even or both odd, the dynamic curve of the overturning moment of the cylinder as a function of its turning angle is drawn using software Matlab. The results show that, when the numbers of pistons inside and outside are both even or both odd, the inside and outside overturning moments of the balanced two-ring axial piston pump can partially or even completely counteract each other. So the overturning moment of the cylinder will significantly reduce and its fluctuation period will remain the same. When the numbers of pistons inside and outside are both odd, the overturning moment will be smaller than that the numbers of pistons inside and outside are both even.

Keyword: fluid power transmission and control; the balanced two-ring axial piston pump; cylinder; equilibrium; overturning moment

Show Figures

基于轴向柱塞泵的结构特点可知, 其缸体始终存在一定程度的倾覆力矩, 从而影响缸体在运转过程中的平稳性和平衡性^{[1, 2]}。倾覆力矩使配流副组件产生偏磨, 导致轴向柱塞泵配流副密封效果不佳, 产生较大泄漏而使轴向柱塞泵无法正常工作^{[3, 4]}。胡骁等^[5]指出, 转子(缸体)固有周期性偏心力矩是配流副油膜产生动态变化的原因, 且配流副油膜始终为楔形。Edge^[6]对轴向柱塞泵的缸体的压力进行试验研究, 指出现有模型不能反映高压高速下的实际工作情况。何必海等^[7]分析了航空燃油轴向柱塞泵配流副的流动特性, 结合挤压效应和热楔效应对配流副油膜厚度的影响, 建立了油膜动态变化方程, 进行了数值计算, 为油膜厚度实时响应的计算提供了一种新方法。

以上研究为普通轴向柱塞泵的设计制造提供了有力支持, 同时文献[8-10]研究了普通多排式轴向柱塞泵的流量脉动。平衡式两排轴向柱塞泵是一种全新轴向柱塞泵, 已有研究证明柱塞合理分布能有效降低其流量脉动, 且优于普通轴向柱塞泵^[11], 但其结构原理不同于普通轴向柱塞泵, 其缸体的受力状况和倾覆力矩也不同于普通轴向柱塞泵。本文分析了平衡式两排轴向柱塞泵运转过程中浮动缸体的平衡性, 推导了缸体倾覆力矩的计算公式, 同时也给出了使缸体、配流盘保持轴向液压力平衡的计算公式和计算程序。本文的研究结果可为普通两排或多排轴向柱塞泵缸体的平衡性提供参考。

1 工作原理

	Figure Option View Download New Window
	图1 平衡式双排轴向柱塞泵结构示意图Fig.1 Diagrammatic sketch of balanced two-ring axial piston pump

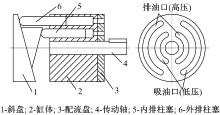
平衡式两排轴向柱塞泵的结构原理如图1所示, 与普通轴向柱塞泵相同, 由缸体、柱塞、配流盘和斜盘等构成。相比于普通轴向柱塞泵, 其斜盘由两个相互倾斜且嵌套的斜面组成, 每个斜盘斜面上分布一排柱塞。当传动轴驱动缸体转动时, 图1中两个斜盘斜面的柱塞往复运动方向相反, 从而导致内外排柱塞的吸排油方向相反, 使缸体两侧都分布有高压油口和低压油口。对应的配流盘上, 高压油口和低压油口也两侧分布。由此可通过合理设计缸体和配流盘的结构尺寸, 使缸体和配流盘保持轴向液压力平衡, 故称该泵为平衡式两排轴向柱塞泵。

2 缸体的受力分析

平衡式两排轴向柱塞泵缸体主要受两个力的作用, 即斜盘对缸体的压紧力和配流盘对缸体的反推力, 这两个力都受到内外排柱塞数奇偶性的影响。依据柱塞数对平衡式两排轴向柱塞泵流量脉动的分析可知, 内、外排柱塞数同为相等奇数或同为相等偶数时, 具有较小的流量脉动^[11]。故主要分析内、外排柱塞数同为相等奇数或同为相等偶数时缸体的受力状态, 不考虑内、外排柱塞数奇偶性相异的情况, 也可不考虑配流盘上三角槽对压力波动的影响。

2.1 斜盘对缸体的作用

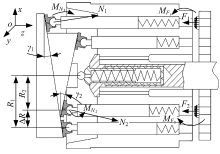
若平衡式两排轴向柱塞泵的内、外排柱塞数均为偶数时, 且将内、外排各有一个柱塞处于其上死点作为缸体转动的起始角, 如图2所示。斜盘对缸体的压紧力和压紧力矩^[12]如下:

$\begin{matrix} \begin{matrix} N_{i} = - \frac{π d_{i}^{2}}{4} m_{i} p_{H} (1) \\ \{\begin{matrix} M_{N_{xi}} = - \frac{π d_{i}^{2}}{4} R_{i} \tan γ_{i} \frac{\cos (φ_{i} - π / z_{i})}{\sin (π / z_{i})} p_{H} \\ M_{N_{yi}} = \frac{π d_{i}^{2}}{4} R_{i} \frac{\cos (φ_{i} - π / z_{i})}{\sin (π / z_{i})} p_{H} \\ M_{N_{zi}} = \frac{π d_{i}^{2}}{4} \frac{R_{i}}{co s^{2} γ_{i}} \frac{\sin (φ_{i} - π / z_{i})}{\sin (π / z_{i})} p_{H} \end{matrix} (2) \end{matrix} \end{matrix}$

式中:i=1, 2, 分别代表内排和外排; m_i为i排处于高压区的柱塞数; d_i为i排的柱塞直径; p_H为泵出口压力; R_i为i排柱塞分布圆直径; z_i为i排柱塞数; γ _i为i排斜盘斜面倾角; φ _i为i排缸体转角。

	Figure Option View Download New Window
	图2 缸体的受力示意图Fig.2 Cylinder’ s force diagram

若平衡式两排轴向柱塞泵的内、外排柱塞数均为奇数时, 其斜盘对缸体压紧力矩如下:

$\begin{matrix} \{\begin{matrix} M_{N_{xi}} = - \frac{π d_{i}^{2}}{4} R_{i} \tan γ_{i} \frac{\cos [φ_{i} - (2 \mp 1) π / 2 z_{i}]}{\sin (π / 2 z_{i})} p_{H} \\ M_{N_{yi}} = \frac{π d_{i}^{2}}{4} R_{i} \frac{\cos [φ_{i} - (2 \mp 1) π / 2 z_{i}]}{\sin (π / 2 z_{i})} p_{H} \\ M_{N_{zi}} = \frac{π d_{i}^{2}}{4} \frac{R_{i}}{co s^{2} γ_{i}} \frac{\sin [φ_{i} - (2 \mp 1) π / 2 z_{i}]}{\sin (π / 2 z_{i})} p_{H} \end{matrix} (3) \end{matrix}$

由于x方向的压紧力矩 $\begin{matrix} M_{N_{xi}} \end{matrix}$ 阻碍了平衡式两排轴向柱塞泵缸体的转动, 可由驱动缸体转动的传动轴相平衡, 保持缸体绕轴转动, 故使缸体产生轴向转动的力矩 $\begin{matrix} M_{N_{i}} \end{matrix}$ 为:

$\begin{matrix} M_{N_{i}} = M_{N_{yi}} + j M_{N_{zi}} (4) \end{matrix}$

2.2 配流盘的反推作用

如图2所示, 由于配流盘与缸体间压力流体的存在, 导致配流盘对缸体产生一定的反推力。不同于普通轴向柱塞泵, 平衡式两排轴向柱塞泵在配流盘的两侧都存在高压区, 故合理设计内、外排的结构尺寸可使配流盘的受力相对平衡。

配流盘的反推力和反推力矩可表示为:

$\begin{matrix} \begin{matrix} F_{i} = - \frac{1}{4} [\frac{R_{4 i}^{2} - R_{3 i}^{2}}{\ln (R_{4 i} / R_{3 i})} - \frac{R_{2 i}^{2} - R_{1 i}^{2}}{\ln (R_{2 i} / R_{1 i})}] φ_{pi} p_{H} (5) \\ \{\begin{matrix} M_{F_{xi}} = 0 \\ M_{F_{yi}} = - \frac{2 p_{H}}{9} [\frac{R_{4 i}^{3} - R_{3 i}^{3}}{\ln (R_{4 i} / R_{3 i})} - \frac{R_{2 i}^{3} - R_{1 i}^{3}}{\ln (R_{2 i} / R_{1 i})}] \\ \sin \frac{φ_{pi}}{2} \sin \frac{φ ″_{i} + φ'_{i}}{2} \\ M_{F_{zi}} = \frac{2 p_{H}}{9} [\frac{R_{4 i}^{3} - R_{3 i}^{3}}{\ln (R_{4 i} / R_{3 i})} - \frac{R_{2 i}^{3} - R_{1 i}^{3}}{\ln (R_{2 i} / R_{1 i})}] \\ \sin \frac{φ_{pi}}{2} \cos \frac{φ ″_{i} + φ'_{i}}{2} \end{matrix} \\ (6) \end{matrix} \end{matrix}$

式中:R₁_i、R₂_i为i排柱塞对应配流盘腰形槽内密封带内、外径; R₃_i、R₄_i为i排柱塞对应配流盘腰形槽外密封带内、外径; φ _pi为i排柱塞对应配流盘的压力角; φ '_i、φ ″_i分别为i排柱塞对应配流盘压力角的起始角和终止角。

使平衡式两排轴向柱塞泵缸体轴向转动总的反推力矩 $\begin{matrix} M_{F_{i}} \end{matrix}$ 为:

$\begin{matrix} M_{F_{i}} = M_{F_{yi}} + j M_{F_{zi}} (7) \end{matrix}$

2.2.1 压力角的确定

由式(6)可知, 压力角、压力角的起始角和终止角的大小决定了反推力的大小和方向, 可用缸体转角φ 的函数表示, 该函数同时也受到轴向柱塞泵柱塞数奇偶性的影响。若缸体上单个柱塞的油口范围角为φ ₁, 配流盘上的封油角为φ ₀。实际上封油角φ ₀稍大于单个柱塞的油口范围角φ ₁, 这样可保持轴向柱塞泵具有良好的密封性, 同时为避免压力突变, 常采用三角槽结构进行压力过渡。为使计算方便, 假设两者相等, 即φ ₁=φ ₀, 且φ ₀> 1.5π /z。由于平衡式两排轴向柱塞泵配流盘存在近似对称的三角槽结构, 其压力过渡的周期基本相同, 故上述假设对计算造成的影响较小。

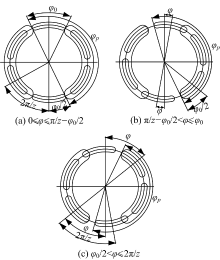
当柱塞数为奇数时, 如图3所示, 可分4种情况讨论压力角:①当0≤ φ ≤ π /z时, φ '=φ -φ ₀/2, φ ″=π +φ -π /2z+φ ₀/2, φ _p=π -π /2z+φ ₀; ②当π /z< φ ≤ 3π /z-φ ₀时, φ '=φ -φ ₀/2, φ ″=π -φ ₀/2, φ _p=π -φ ; ③当3π /z-φ ₀< φ ≤ φ ₀时, φ '=φ -φ ₀/2, φ ″=π +φ +φ ₀/2-3π /z, φ _p=π -3π /z+φ ₀; ④当φ ₀< φ ≤ 2π /z时, φ '=φ ₀/2, φ ″=π +φ +φ ₀/2-3π /z, φ _p=π -3π /z+φ 。

	Figure Option View Download New Window
	图3 奇数柱塞压力角的分布Fig.3 Pressure angle’ s distribution when the number of the piston is odd

当柱塞数为偶数时, 如图4所示, 可分3种情况讨论压力角:①当0≤ φ ≤ π /z-φ ₀/2时, φ '=φ -φ ₀/2, φ ″=π -φ ₀/2, φ _p=π -φ ; ②当π /z-φ ₀/2< φ ≤ φ ₀时, φ '=φ -φ ₀/2, φ ″=π +φ -2π /z+φ ₀/2, φ _p=π -2π /z+φ ₀; ③当φ ₀/2< φ ≤ 2π /z时, φ '=φ ₀/2, φ _p=π -2π /z+φ , φ ″=π +φ -2π /z+φ ₀/2。

	Figure Option View Download New Window
	图4 偶数柱塞压力角的分布Fig.4 The pressure angle’ s distribution when the number of the piston is even

2.2.2 密封带尺寸的确定

平衡式两排轴向柱塞泵密封带的基本尺寸存在如下关系^[13]:

$\begin{matrix} \begin{matrix} R_{2 i} - R_{1 i} = 0.125 d_{i} (8) \\ R_{4 i} - R_{3 i} = 0.1 d_{i} (9) \\ R_{2 i} + R_{3 i} = 2 R_{i} (10) \end{matrix} \end{matrix}$

式(8)(9)(10)为轴向柱塞泵配流盘设计的一般性经验公式。为保证平衡式两排轴向柱塞泵缸体受力平衡, 应满足:

$\begin{matrix} N_{1} + N_{2} = ε (F_{1} + F_{2}) (11) \end{matrix}$

式中:ε 为压紧系数, ε =1.05。

鉴于平衡式两排轴向柱塞泵可视为两个普通轴向柱塞泵的组合, 平衡式轴向柱塞泵配流盘密封带尺寸可分别进行计算:

$\begin{matrix} \begin{matrix} N_{1} = ε F_{1} (12) \\ N_{2} = ε F_{2} (13) \end{matrix} \end{matrix}$

由式(1)(5)(12)(13)可得:

$\begin{matrix} \frac{R_{4 i}^{3} - R_{3 i}^{3}}{\ln (R_{4 i} / R_{3 i})} - \frac{R_{2 i}^{3} - R_{1 i}^{3}}{\ln (R_{2 i} / R_{1 i})} = ε \frac{π m_{i} d_{i}^{2}}{2} (14) \end{matrix}$

联解式(8)(9)(10)(11)(14), 即可确定平衡式两排轴向柱塞泵配流盘密封带的基本尺寸, 由此即可决定平衡式两排轴向柱塞泵的反推力和反推力矩。若使N₁=N₂、F₁=F₂, 平衡式两排轴向柱塞泵的缸体和配流盘的轴向液压力均保持平衡, 由于缸体和配流盘都是两侧受力, 更有利于缸体的稳定。通过编制程序解非线性方程组, 即可得出缸体、配流盘轴向液压力平衡时的结构参数。

3 缸体的平衡性分析

由平衡式两排轴向柱塞泵缸体的受力分析(见图2)可得出决定其缸体平衡性最关键的参数倾覆力矩M_z为:

$\begin{matrix} M_{z} = M_{F_{1}} + M_{N_{2}} - M_{F_{2}} - M_{N_{1}} (15) \end{matrix}$

依据以上分析, 分别取平衡式两排轴向柱塞泵内、外排柱塞的分布圆半径R₁、R₂分别为40 mm和50 mm, 取泵出口压力p_H为16 MPa。利用Matlab编程确定配流盘结构尺寸, 由分布圆直径计算出各自密封带的半径值, 同时计算出缸体各个力矩随缸体转角变化的情况, 并按照平衡式两排轴向柱塞泵内外排柱塞数的奇偶性来考察其缸体倾覆力矩的情况。

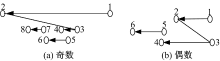
	Figure Option View Download New Window
	图5 奇数时力矩极坐标图Fig.5 Moment of polar coordinates when the number of the piston is odd

首先考察内外柱塞数均为奇数时缸体的倾覆力矩。图5为内、外排柱塞数均为7个时, 平衡式两排轴向柱塞泵缸体所受4个力矩的变化轨迹的极坐标图。由图可见, 平衡式两排轴向柱塞泵内、外排的压紧力矩和反推力矩的矢量均在π /z角度范围内变化, 且同一排的压紧力矩和反推力矩的方向大致相反。对反推力矩而言, 由图5(b)和图6(a)可见, 其运动轨迹为1→ 2跳至3→ 4→ 5→ 6→ 7→ 8跳至1, 由此循环。对压紧力矩而言, 见图5(c), 压紧力矩轨迹从上面曲线由右至左, 再从下面曲线由左至右, 由此完成一个完整的循环。

	Figure Option View Download New Window
	图6 反推力矩轨迹示意图Fig.6 Diagram of the reverse thrust moment’ s trace

图7为内、外排柱塞数均为6个时平衡式两排轴向柱塞泵缸体所受4个力矩变化轨迹的极坐标图。由图可见, 平衡式两排轴向柱塞泵的压紧力矩和反推力矩的矢量均在2π /z角度范围内变化, 同时同一排的压紧力矩和反推力矩的方向也近似相反。与图5相同, 按照式(14)设计轴向柱塞泵的结构尺寸并不能使同排的压紧力矩和反推力矩的大小相等。对反推力矩而言, 由图7(b)和图6(b)可见, 其运动轨迹为1→ 2跳至3→ 4→ 5→ 6跳至1, 如此循环。对压紧力矩而言, 见图7(c), 其轨迹由右运动至左, 再跳至右, 如此循环。

	Figure Option View Download New Window
	图7 偶数时力矩极坐标图Fig.7 Moment of polar coordinates when the number of the piston is even

综合图5、图6和图7可知:不论内、外排柱塞数均为偶数或奇数, 其反推力矩和压紧力矩均不相等, 其方向近似相反, 内、外排始终存在倾覆力矩。与压紧力矩不同, 反推力矩的方向和大小均随缸体转角周期性变化。由此可见, 对普通单排轴向柱塞泵而言, 压紧力矩不可能与反推力矩大小相等, 方向相反。而对平衡式两排轴向柱塞泵而言, 可使内、外排反推力矩与压紧力矩均大小相等, 方向相反, 由此使平衡式两排轴向柱塞泵的倾覆力矩在理论上近似为零。

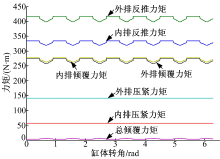
图8为平衡式两排轴向柱塞泵的各种力矩幅值随缸体转角的变化情况, 参数条件与图5相对应。由图可见, 由于内、外排设置相同的柱塞数, 故内、外排的反推力矩的波动周期相同, 且方向相反。同时, 内、外排的压紧力矩的幅值基本恒定, 可以最大程度地相互抵消, 故平衡式两排轴向柱塞泵总的倾覆力矩很小, 平均值为3.6827 Nm, 远小于内排倾覆力矩平均值272.7556 Nm和外排倾覆力矩平均值269.0729 Nm, 且总的倾覆力矩的最大值与最小值之差仅为3.6804 Nm, 远小于内排的14.9427 Nm和外排的18.6232 Nm。因此, 平衡式两排轴向柱塞泵缸体的平衡性要优于普通单排轴向柱塞泵。

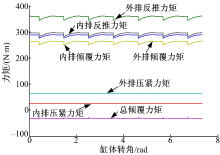
	Figure Option View Download New Window
	图8 奇数时力矩随转角的变化Fig.8 Moment changing in turn angle when the number of the piston is odd

图9为平衡式两排轴向柱塞泵各种力矩幅值随缸体转角的变化情况, 参数条件与图6相对应。当内、外排柱塞数为偶数时, 其总的倾覆力矩也小于内排倾覆力矩和外排倾覆力矩。总的倾覆力矩的平均值为32.8996 Nm, 最大值与最小值之差为3.2625 Nm, 相对应的内排分别为260.5547、13.2021 Nm, 外排分别为293.4544、16.4646 Nm。内、外排柱塞数为偶数时总的倾覆力矩大于奇数时总的倾覆力矩。

	Figure Option View Download New Window
	图9 偶数时力矩随转角的变化Fig.9 Moment changing in turn angle when the number of the piston is even

图8和图9都表明平衡式两排轴向柱塞泵内、外排的倾覆力矩相互抵消, 从而大大降低了平衡式两排轴向柱塞泵总的倾覆力矩。同时, 也可通过合理优化配流盘和缸体的结构尺寸, 进一步控制总的倾覆力矩的大小, 提高平衡式两排轴向柱塞泵的平衡性。

4 结论

(1)通过Matlab编程计算表明, 当内、外排柱塞数同为奇数或偶数时, 平衡式两排轴向柱塞泵浮动缸体的平衡性要优于普通轴向柱塞泵。其原因在于内外排的倾覆力矩可相互抵消, 使总的倾覆力矩减小, 但倾覆力矩的波动周期保持不变。

(2)内外排柱塞数同为奇数时的倾覆力矩优于内、外排柱塞数同为偶数时的倾覆力矩, 通过合理设计缸体和配流盘的结构尺寸, 可进一步减小其倾覆力矩。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	熊小平, 于兰英, 王国志, 等. 轴向柱塞泵球面配流盘倾覆力浅析[J]. 流体传动与控制, 2009(4): 25-28. Xiong Xiao-ping, Yu Lan-ying, Wang Guo-zhi, et al. The adventure analysis of spherieal valve plate in axial piston pump[J]. Fluid Power Transmission and Control, 2009 (4): 25-28. [本文引用:1]
[2]	童水光, 王相兵, 钟崴, 等. 基于虚拟样机技术的轴向柱塞泵动态特性分析[J]. 机械工程学报, 2013, 49(2): 174-182. Tong Shui-guang, Wang Xiang-bing, Zhong Wei, et al. Dynamic characteristics analysis on axial piston pump based on virtual prototype technology[J]. Journal of Mechanical Engineering, 2013, 49(2): 174-182. [本文引用:1]
[3]	Bergada J, Kumar S, Davies D L, et al. A complete analysis of axial piston pump leakage and output flow ripples[J]. Applied Mathematical Modelling, 2012, 36(4): 1731-1751. [本文引用:1]
[4]	Bergada J, Davies D L, Kumar S, et al. The effect of oil pressure and temperature on barrel film thickness and barrel dynamics of an axial piston pump[J]. Meccanica, 2012, 47(3): 639-654. [本文引用:1]
[5]	胡骁, 王少萍, 韩磊. 轴向柱塞泵配流副动态压力分布建模与仿真[J]. 液压气动与密封, 2012, 32(8): 68-71. Hu Xiao, Wang Shao-ping, Han Lei. Modeling and simulation on pressure distribution of plane port pair in axial piston pump[J]. Hydraulics Pneumatics & Seals, 2012, 32(8): 68-71. [本文引用:1]
[6]	Edge K A, Darling J. Cylinder pressure transients in oil hydraulic pumps with sliding plate valves[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 1986, 200(1): 45-54. [本文引用:1]
[7]	何必海, 孙健国, 叶志锋. 燃油柱塞泵滑靴副和配流副油膜计算研究[J]. 航空动力学报, 2010, 25(6): 1437-1442. He Bi-hai, Sun Jian-guo, Ye Zhi-feng. Calculation and analysis of film thickness for slipper pair and valve plate pair in fuel piston pump[J]. Journal of Aerospace Power, 2010, 25(6): 1437-1442. [本文引用:1]
[8]	杨逢瑜, 马毓姝, 温亚飞, 等. 双排式轴向柱塞泵的流量脉动分析[J]. 兰州理工大学学报, 2010, 36(6): 45-47. Yang Feng-yu, Ma Yu-shu, Wen Ya-fei, et al. Analyses of flow pulsation in double-ring axial piston pump[J]. Journal of Lanzhou University of Technology, 2010, 36(6): 45-47. [本文引用:1]
[9]	陈进, 方建忠, 李世六, 等. 多排式轴向柱塞泵的流体动力特性研究[J]. 建筑机械, 2007(9): 89-93. Chen Jin, Fang Jian-zhong, Li Shi-liu, et al. Fluid dynamic property study of may rows type axial piston pump[J]. Construction Machinery, 2007(9): 89-93. [本文引用:1]
[10]	纪平. 双排式轴向柱塞泵柱塞的受力与分析[J]. 液压与气动, 2011(4): 152-155. Ji Ping. Plunger dynamics analysis of double-row-type axial piston pump[J]. Chinese Hydraulics & Pneumatics, 2011(4): 152-155. [本文引用:1]
[11]	邓海顺, 王传礼, 张立祥. 平衡式两排轴向柱塞泵流量脉动的研究[J]. 农业机械学报, 2014, 45(5): 305-309. Deng Hai-shun, Wang Chuan-li, Zhang Li-xiang. Study on flow ripple of balanced two-ring axial piston pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(5): 305-309. [本文引用:2]
[12]	李壮云. 液压元件与系统[M]. 2版. 北京: 机械工业出版社, 2008. [本文引用:1]
[13]	何存兴. 液压传动与气压传动[M]. 武汉: 华中科技大学出版社, 2000. [本文引用:1]

2009

0.0

. 2009, 2009(4):25-28 DOI:doi:10.3969/j.issn.1672-8904.2009.04.009

The adventure analysis of spherieal valve plate in axial piston pump

Xiong Xiao-ping , Yu Lan-ying , Wang Guo-zhi

熊小平, 于兰英, 王国志

通过对斜盘式轴向柱塞泵中平面配流盘配流与球面配流盘配流的力学特性的分析,在其它因素都相同的情况下,球面配流盘配流的抗倾覆力矩能力强的特点.

... 基于轴向柱塞泵的结构特点可知,其缸体始终存在一定程度的倾覆力矩,从而影响缸体在运转过程中的平稳性和平衡性^[1,2] ...

2013

0.0

. 2013, 49(2):174-182 DOI:doi:10.3901/JME.2013.02.174

Dynamic characteristics analysis on axial piston pump based on virtual prototype technology

基于虚拟样机技术的轴向柱塞泵动态特性分析

Tong Shui-guang , Wang Xiang-bing , Zhong Wei

童水光, 王相兵, 钟崴

为开发新式高性能轴向柱塞泵,在分析柱塞泵工作原理和运动规律的基础上,采用Kane-Huston方法建立轴向柱塞泵机液耦合作用的多体力学模型,根据轴向柱塞泵流体特性及控制原理建立其液压系统模型,并构建二者实时接口连接的虚拟样机模型.建立某型号斜盘式轴向柱塞泵的虚拟样机模型并进行数值求解和仿真模拟,数值计算和仿真结果基本一致.研究柱塞泵机-液耦合作用下的运动特性,泵出口流量及压力脉动特性以及柱塞泵的流量控制特性,并研究柱塞泵相应动态特性的影响因素及其变化规律.基于虚拟样机技术的建模、仿真研究方法,能够全方位预测轴向柱塞泵的各项性能,正成为轴向柱塞泵性能研究的重要手段.

... 基于轴向柱塞泵的结构特点可知,其缸体始终存在一定程度的倾覆力矩,从而影响缸体在运转过程中的平稳性和平衡性^[1,2] ...

2012

0.0

... 倾覆力矩使配流副组件产生偏磨,导致轴向柱塞泵配流副密封效果不佳,产生较大泄漏而使轴向柱塞泵无法正常工作^[3,4] ...

2012

0.0

... 倾覆力矩使配流副组件产生偏磨,导致轴向柱塞泵配流副密封效果不佳,产生较大泄漏而使轴向柱塞泵无法正常工作^[3,4] ...

2012

0.0

. 2012, 32(8):68-71 DOI:doi:10.3969/j.issn.1008-0813.2012.08.023

Modeling and simulation on pressure distribution of plane port pair in axial piston pump

轴向柱塞泵配流副动态压力分布建模与仿真

Hu Xiao , Wang Shao-ping , Han Lei.

胡骁, 王少萍, 韩磊

为了获得轴向柱塞泵平面配流副的动态压力分布,基于雷诺(Reynolds)方程推导了柱坐标下封油带内任一点的压力计算模型,根据转子转动角度动态更新边界条件,利用有限差分法求解配流副油膜的动态压力分布。结果表明,配流副油膜压力在封油带内呈非线性,并且会产生使转子偏转的固有偏心力矩以及周期性偏心力矩,从而导致配流副油膜的动态变化。

... 胡骁等^[5]指出,转子(缸体)固有周期性偏心力矩是配流副油膜产生动态变化的原因,且配流副油膜始终为楔形 ...

1986

0.0

... Edge^[6]对轴向柱塞泵的缸体的压力进行试验研究,指出现有模型不能反映高压高速下的实际工作情况 ...

2010

0.0

. 2010, 25(6):1437-1442

Calculation and analysis of film thickness for slipper pair and valve plate pair in fuel piston pump

燃油柱塞泵滑靴副和配流副油膜计算研究

He Bi-hai , Sun Jian-guo , Ye Zhi-feng.

何必海, 孙健国, 叶志锋

通过分析航空燃油柱塞泵滑靴副及配流副间油液的流动特点,综合考虑挤压效应,热楔效应对油膜厚度的影响,得到满足滑靴副及配流副油膜变化的统一微分方程,通过求解方程,可计算得到滑靴副和配流副油膜厚度在柱塞旋转一周内的变化规律,弥补传统静压支承油膜计算方法的不足.

... 何必海等^[7]分析了航空燃油轴向柱塞泵配流副的流动特性,结合挤压效应和热楔效应对配流副油膜厚度的影响,建立了油膜动态变化方程,进行了数值计算,为油膜厚度实时响应的计算提供了一种新方法 ...

2010

0.0

. 2010, 36(6):45-47 DOI:doi:10.3969/j.issn.1673-5196.2010.06.012

Analyses of flow pulsation in double-ring axial piston pump

双排式轴向柱塞泵的流量脉动分析

Yang Feng-yu , Ma Yu-shu , Wen Ya-fei

杨逢瑜, 马毓姝, 温亚飞

针对轴向柱塞泵为降低流量脉动率而采用奇数柱塞使流量调节范围有限的问题,采用双排柱塞设计轴向柱塞泵,并对双排式轴向柱塞泵的结构及流量脉动特性进行研究.计算、仿真和实验结果表明:在缸质量和体积增大不多的前提下通过增加工作柱塞排数,可使泵的排量增大、流量脉动率减小、流量调节范围扩大.推导出的双排式轴向柱塞泵的理论流量计算公式经过计算机仿真和实验验证与实际接近.

0.0

. , 2007(9):89-93 DOI:doi:10.3969/j.issn.1001-554X.2007.09.023

Fluid dynamic property study of may rows type axial piston pump

多排式轴向柱塞泵的流体动力特性研究

Chen Jin , Fang Jian-zhong , Li Shi-liu

陈进, 方建忠, 李世六

研究了多排式轴向柱塞泵的工作原理、功能特点及应用前景,并以该泵为例,利用Pumplinx泵用软件对其进行了建模、仿真分析和空化预测。针对原设计左端盖中存在的弊端,着重分析了其空化产生的机理,并以提高空化系数为目标,从入口压力和结构优化2个方面在理论上进行了探讨,推出了与提高空化系数相关的数学公式,并提出了增大入口压力的改进措施,设计了有利于减小压降的新型端盖,有效地抑制了空化的产生。结果表明,应用Pumplinx泵用软件对多排式轴向柱塞新型泵进行流体动力特性分析验证,结果准确可靠。分析表明该泵各项性能指标优异,通过改良,泵的空化问题得到有效控制,为提高泵的容积效率和降低噪声提供了参考依据。

0.0

. , 2011(4):152-155 DOI:doi:10.3969/j.issn.1000-4858.2011.04.030

双排式轴向柱塞泵柱塞的受力与分析

Ji Ping.

纪平

柱塞的受力状况影响到双排式轴向柱塞泵的效率和寿命,是设计中的关键环节.柱塞随缸体旋转时受到离心力的作用,由于柱塞的质量中心与转动中心不重合,离心力引起柱塞的翻转.通过对柱塞的受力分析,确定了柱塞受力特性,该研究不仅对克服双排式轴向柱塞泵缸体所受的倾覆力矩和防止缸体倾斜提供了计算结果,而且为柱塞的选择给出了设计依据.

2014

0.0

. 2014, 45(5):305-309 DOI:doi:10.6041/j.issn.1000-1298.2014.05.047

Study on flow ripple of balanced two-ring axial piston pump

平衡式两排轴向柱塞泵流量脉动的研究

Deng Hai-shun , Wang Chuan-li , Zhang Li-xiang.

邓海顺, 王传礼, 张立祥

The balanced two-ring axial piston pump has a different characteristic of flow ripple because of its improved structure. The flow rippleis analyzed when the numbers of the piston inside and outside are even or odd. And its instantaneous flow’s curves are drawn by Matlab, based on the different parameters. The results show that when the numbers of the piston inside and outside are unequal even or unequal odd, the instantaneous flow inside and outside will counteract, and the flow ripple will reduce. When the numbers of the piston inside and outside are equal even or equal odd, the instantaneous flow inside and outside will overlap, and the flow ripple will remain unchanged. When the numbers of the piston inside and outside are equal and the piston inside and outside are arranged in cross, the pump has the minimum flow ripple, the ripple period is half of that of ordinary axial piston pump, and the pump’s structure is more compact.

平衡式两排轴向柱塞泵的结构特点，决定了其流量脉动不同于普通轴向柱塞泵。分析了内外柱塞数同为奇数或偶数的平衡式两排轴向柱塞泵的流量脉动情况，采用不同参数，利用Matlab绘制其瞬时流量曲线进行比较。结果表明：内外排柱塞数同为不相等的奇数或偶数时，内外排瞬时流量存在抵消使流量脉动减小。内外排柱塞数为相同的奇数或偶数时，内外排瞬时流量互相叠加使流量脉动保持不变。内外排柱塞数相等且交叉布置时，其流量脉动具有最大的减小量，脉动周期为普通轴向柱塞泵的一半，有利于泵结构的紧凑。

... 平衡式两排轴向柱塞泵是一种全新轴向柱塞泵,已有研究证明柱塞合理分布能有效降低其流量脉动,且优于普通轴向柱塞泵^[11],但其结构原理不同于普通轴向柱塞泵,其缸体的受力状况和倾覆力矩也不同于普通轴向柱塞泵 ...

... 依据柱塞数对平衡式两排轴向柱塞泵流量脉动的分析可知,内、外排柱塞数同为相等奇数或同为相等偶数时,具有较小的流量脉动^[11] ...

2008

0.0

... 斜盘对缸体的压紧力和压紧力矩^[12]如下: ...

2000

0.0

. 2000, :-

何存兴

本书包括随机过程的概念，泊松过程，马尔可夫链等内容。

... 平衡式两排轴向柱塞泵密封带的基本尺寸存在如下关系^[13]: ...