作者简介:滕菲(1985-),女,博士研究生.研究方向:汽车材料.E-mail:tengfei325@126.com
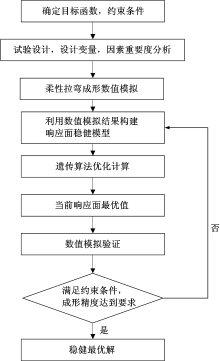
分析了型材柔性三维拉弯成形工艺的可控因素和不可控因素,提出了该工艺稳健分析优化设计方法。通过有限元模拟,对可控因素和不可控因素进行正交试验分析,找出了影响较大的因素。采用在减小回弹的基础上控制型材厚度变化率的综合质量损失为目标函数,用响应面模型对其进行函数拟合,然后利用遗传算法对目标函数进行稳健优化。试验验证结果表明:采用该方法进行稳健优化设计后,能够在满足约束条件的情况下有效减小综合质量损失。
The uncontrollable factors and controllable factors of the profile of three-dimensional flexible stretch bending forming are analyzed. Based on the analysis, a comprehensive quality evaluation method of three-dimensional stretch bending and a robust optimization method are proposed. The uncontrollable factors and controllable factors are analyzed based on orthogonal experiments by finite element simulations, and the factors greatly influencing the forming quality are identified. The comprehensive quality evaluation method is established using the loss of comprehensive quality as the optimization objective. The objective includes reducing the springback and controlling the change rate of profile thickness. The response surface model is adopted to carry out the fitting function. Genetic algorithm is applied for robust optimization, and the optimization results are validated. The results show that the robust optimization method can effectively reduce the comprehensive quality loss while the constraints are satisfied.
近年来, 铝型材在汽车、飞机和高铁列车的承载结构件制造领域得到广泛的应用[1]。拉弯工艺是铝型材主要的加工方法之一, 随着汽车和高铁等工业的发展, 二维拉弯工艺已不能满足工业需求, 三维拉弯工艺开始发展。铝型材三维拉弯成形质量受到很多因素的影响, 其中回弹是影响成形质量的主要原因[2, 3]。Tryand等[4]对铝型材的力学性能进行了系统研究, 发现铝型材具有明显的各向异性。Miller等[5, 6]发现减小预拉力可降低截面畸变程度, 增加补拉力能有效减小回弹。Hopperstad等[7]通过试验发现屈服应力和硬化特性对回弹量影响很大, 而各向异性对回弹的影响相对较小。
稳健优化设计是指虽然改变产品在制造中的参数, 产品性能仍可以保证的一种设计方法, 优化后的最优解具有较强的抗干扰能力[8, 9]。Tang等[10]采用径向基函数构造了自适应的代理模型用于板料成形稳健性分析, 优化后零件回弹量和减薄率均有所改善。谢延敏[11]基于动态的Kriging模型对板料成形进行了工艺稳健设计, 优化后的标准差有明显的降低。郭宝峰等[12]提出了一种塑性成形工艺参数稳健性设计方法, 该方法以形状精度和尺寸为控制对象。稳健性分析已广泛应用于板料成形工艺, 然而在拉弯工艺成形领域稳健性研究还没有得到广泛应用[13]。
本文对三维拉弯成形进行了稳健性分析和稳健优化设计。采用有限元模拟对拉弯成形工艺的可控因素和不可控因素进行研究, 并提出综合成形质量损失判定方法。基于响应面模型和遗传算法对其进行稳健优化设计, 并用拉弯成形试验进行验证。
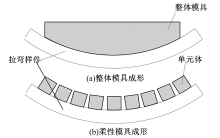
柔性三维拉弯成形模具采用若干离散单元体代替整体模具作为成形设备, 如图1所示。柔性拉弯模具成形面是由装配在离散单元体上的成形滑块组成的。单元体安装在一个独立支架上, 单元体可进行前后位移调整, 成形滑块可以上下位移调整和在水平面及垂直面内旋转, 所以柔性成形模具的成形面是可重构的。对于不同几何形状的型材只需更换相应几何形状的成形滑块和夹钳即可, 这可以有效减小成本。
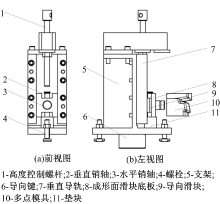
每个单元体由成形面滑块、支架、导向滑块和导轨等部件组成, 如图2所示。高度控制螺杆可以控制单元体模具高度, 其高度可以控制型材形状。垂直销轴控制成形滑块的高度; 水平销轴是成形滑块与单元体的连接件; 螺栓连接单元体与拉弯机的工作台; 支架支撑单元体构件; 导向滑块使成形滑块限位限向移动; 垂直导轨使成形滑块及连接件可以沿其轨道滑动; 导向滑块引导单元体装置沿着拉弯机在工作台面移动; 垫块是成形滑块的下控制点。
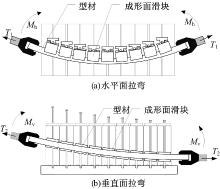
三维拉弯是指在两个相互垂直的平面内均有拉弯成形的工艺。柔性三维拉弯成形将三维拉弯分解为水平面拉弯和垂直面拉弯, 如图3所示。通过单元体位置移动和成形滑块旋转, 柔性三维拉弯的模具成形面可以在水平面和垂直面灵活修改, 故可以完成三维拉弯成形。
响应面模型是在试验设计基础上用于处理多变量问题建模的统计方法。响应面法最初是由Box和Wilson[14]提出, 它可以通过函数来拟合系统输入值与输出值之间关系, 从而简化问题和提高效率。柔性拉弯成形工艺稳健设计中, 不仅需要拟合柔性拉弯成形过程的输入和输出, 还需要计算优化目标函数值, 因此响应面模型可以作为一个有效的替代模型。
首先确定拉弯工艺的设计变量、约束变量和优化目标。通过这些变量设计方案, 进行数值模拟, 筛选出对目标函数影响较大的因素。利用这些筛选结果建立响应面模型, 并对拟合结果进行精度验证。
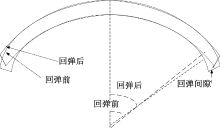
型材在拉弯成形过程中易出现回弹、起皱和断裂等成形缺陷。其中回弹是影响型材成形尺寸精度的主要因素, 它与整个成形过程密切相关。回弹量的判定有多种方法, 本文采用回弹后型材端点位置参考点与目标形状的回弹间隙来评价回弹大小, 如图4所示。回弹量是成形质量的重要参数, 减小回弹是拉弯成形优化的目标之一。
提高拉弯成形的质量是尽量减小回弹、起皱和断裂等成形缺陷。通过增加预拉量和补拉量可以减少回弹量, 但是同时容易引起起皱和破裂等问题。因此以起皱和破裂作为减小回弹的优化目标的约束条件。成形极限图可以表示拉弯成形过程中的起皱和破裂。但是精确的成形极限图不易得到, 目前已有很多研究采用型材的厚度率变化作为成形极限的判别标准。因此本文用厚度变化率作为优化的约束条件, 厚度变化率计算方法如下:
式中:Δ tmax和Δ tmin分别定义为成形后最大单元厚度变化率和最小单元厚度变化率; t0为成形前的单元厚度; tmax、tmin分别为成形后最大、最小单元厚度; 型材成形后质量的约束为:0≤ Δ tmax≤ 0.15, 0.02≤ Δ tmin≤ 0.03。
由上面的讨论可知, 在减小回弹的基础上型材的厚度变化也要有所约束。型材三维拉弯成形后的质量评价应该采用综合质量评价。Chen[15]提出一种基于信噪比的多元质量特性的稳健优化模型。郭宝峰等[12]在此基础上提出了一种综合质量损失评价方法。综合质量损失是指将信噪比转变为标准的质量损失后再加权求和。塑性成形工艺的稳健优化的标准质量损失为[12]:
式中:yi为标准质量损失, i为1到n的整数, n是指有n个质量损失考核指标; K为质量损失系数; L为最大质量损失; η 为信噪比, 信噪比是通过内、外表实验结果进行计算得到的。
式中:yz为综合质量损失; α i为标准质量损失的权重。权重系数α i的取值具有实际意义, 它能够反映出每个质量损失指标对稳健性要求的高低。权重系数α i值在0到1之间, α i值越高, 就表示该质量特性对稳健性的要求越高, 同时该因素对目标函数值的影响越显著。
用综合质量损失来评价拉弯成形后的质量, 可以把多目标的优化问题转化为单目标优化的问题。采用综合质量损失作为稳健优化的目标, 设计变量与它的关系可以在试验的基础上通过响应面模型建立。
基于响应面和遗传算法的柔性三维拉弯成形工艺稳健设计流程如图5所示。
型材柔性拉弯成形质量影响因素除了型材本身的截面形状和材料性能, 还有工艺参数以及在成形过程中可能出现的随机因素。敏感性分析可以获得影响拉弯工艺质量最为敏感的材料性能和工艺因素。可以通过在成形过程中严格控制这些敏感参数的波动范围来提高拉弯成形的质量。
在柔性拉弯成形过程中, 影响成形质量的参数主要有型材的几何参数、材料性能和工艺参数等。根据稳健性分析, 过程参数可以根据其性质分为可控因素和不可控因素。可控因素是指在工艺设计和优化中可以被人为改变的参数; 另一类在工艺设计中不能人为的改变或者不容易控制的因素称为不可控因素。通常情况下, 几何参数和工艺参数是可控因素, 材料性能和摩擦条件是不可控因素。
对于柔性三维拉弯成形过程中可控因素和不可控因素都较多。如果在工艺稳健性优化设计中将这些因素都考虑会增加试验次数, 而且不利于对试验结果的分析。为了简化优化设计, 需要有效地减少试验次数。因此在选择敏感因素时可借助正交试验来筛选出对试验结果敏感的因素, 略去不敏感的因素。
常用的稳健设计的试验方案是采用内、外表结合的方式。内表为可控因素, 外表为不可控因素, 试验方案为内外表的直积。考虑到对拉弯工艺成形结果影响较大的因素, 不可控因素选用材料的弹性模量、屈服应力、硬化指数、各项异性、抗拉强度和摩擦因数。对这些不可控因素影响程度采用L16(45)正交试验进行评估。结果表明, 弹性模量、屈服应力、硬化指数和摩擦因数是相对较为重要的不可控因素。同样地, 对三维拉弯成形的可控因素进行分析, 选用预拉伸量、补拉伸量、型材厚度与宽度的比值、型材长度和柔性模具设置等进行正交试验。试验采用有限元方法进行模拟, 试验结果表明, 目标形状一定时, 预拉伸量、补拉伸量、宽度与厚度的比值和型材厚度是对拉弯成形后质量影响较大的因素。
| 表1 内表因素水平表 Table 1 Parameters in inner table and their levels |
| 表2 外表因素水平表 Table 2 Parameters in outside table and their levels |
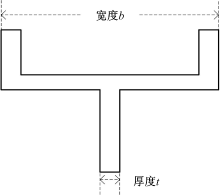
本文采用商业软件ABAQUS进行有限元模拟。选用复杂T型材为研究对象。复杂T型材几何形状如图6所示。使用的材料为铝型材AA6082, 材料参数如下:弹性模量E=71 000 MPa; 泊松比ν =0.345; 初始屈服应力σ 0=139.5 MPa; 应变强化参数Q1=17 MPa; C1=2300; Q2=168 MPa; C2=13。三维拉弯模型包括型材、柔性模具和夹钳3个部分。夹钳可以方便对型材施加拉力和弯矩的作用, 以及对型材与模具边缘位置的控制。夹钳和拉弯模具在拉弯成形过程中的变形量较小, 为了提高模拟运算速度, 选用不需要计算变形的离散刚体壳。
而型材在成形过程中需要计算变形量, 故选用可变形的实体单元。离散的单元体模具组成弧度π /6的弧面, 型材拉伸长度为1 m。柔性三维拉弯模型如图7所示。拉弯过程分为4个阶段, 预拉阶段、水平面拉弯, 垂直面拉弯和补拉阶段。在预拉阶段夹钳参考点的平动自由度放开, 并对夹钳设置预拉量的边界条件。型材受到由夹钳施加的长度方向的拉力。在水平面拉弯阶段离散模具的参考点固定。型材受到弯矩和拉力的作用, 通过夹钳的位移边界条件设置使型材逐渐贴合成形面。垂直面拉弯阶段, 首先将离散模具进行位移调整成为垂直面拉弯模具形状, 然后再通过夹钳的位移控制使得型材逐渐贴模。最后补拉阶段, 为了减少残余应力从而减小回弹, 型材会受到成形后长度方向的补拉力作用。
响应面法可以用于处理多变量的建模问题, 采用近似函数拟合输入和输出值之间关系。响应面法通常采用多项式来拟合系统输出和系统随机输入变量间的关系。型材拉弯成形属于非线性问题, 常用解决非线性问题的响应面方法为二阶响应面模型:
式中:m和n为1到h之间的整数, h为因素的个数; β 0、β m、β mm、
采用最小二乘法对二阶响应面模型系数进行计算, 并对其精度进行检验。本文选用R2作为验证方法, R2反映了响应面值与真值差异程度, 取值为0到1之间, 值为1表示二者完全相同。本文选用其中的20个响应面值计算R2, 得到R2的值为0.9832, 大于0.98表示该响应面模型可以达到较高的精度。故二阶多项式适用于拟合型材拉弯成形。
式中:N为试验设计空间检验点的个数; zl和
对结果采用非支配遗传算法进行优化, 综合质量损失最小化为稳健优化的目标。遗传算法种族的规模设为12, 经过18代遗传216次循环迭代, 得到优化结果为x1=0.7%, x2=0.76%, x3=16.7, x4=7, yz的最小值为0.093。
对柔性三维拉弯成形稳健优化结果进行拉弯成形试验验证。表3为随机抽取3组试验数据与优化后参数拉弯成形试验数据进行对比。其中试验1采用优化后工艺参数, 由表3可以看出试验1综合质量损失最小。优化后型材厚度变化率Δ tmax=0.092, Δ tmin=0.024。可见, 优化后成形质量满足约束条件。增大预拉量和补拉量能够有效减小回弹, 但是同时也容易引起成形截面质量失稳。型材宽度与厚度的比值对回弹影响并不是很大, 但是对型材起皱和断裂影响较大, 比值越小, 越易增加起皱失稳。型材厚度增加可以有效增加抗起皱能力, 但是会减小型材宽度与厚度的比值, 故型材厚度需要进行控制和优化。优化后结果是对多个目标优化后的参数, 可同时减小回弹和起皱。
| 表3 实验数据 Table 3 Experiments data |
通过对型材拉弯成形质量有影响的不可控因素和可控因素进行试验分析, 发现弹性模量、屈服应力、硬化指数和摩擦因数是影响较大的因素。提出了型材三维拉弯成形稳健分析模型, 模型采用响应面对型材三维拉弯成形后综合质量损失进行拟合, 并用遗传算法对其进行优化。采用该稳健优化模型对柔性三维拉弯成形实例进行稳健优化, 并验证了优化结果。结果表明, 该稳健优化模型能在满足约束条件下将综合质量损失减小至0.093。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|