作者简介:邢保英(1986-),女,博士研究生.研究方向:薄板材料连接新技术.E-mail:xbb0808@163.com
以3颗铆钉连接的5052铝合金自冲铆接头为对象,通过试验的方法研究多铆钉自冲铆接头力学性能机理。获得了m-o自冲铆接头(简称m-o接头)和m-i自冲铆接头(m-i接头)的静力学和疲劳试验数据,选择正态分布和二参数威布尔分布检验数据的有效性,通过最小二乘法获得疲劳寿命最佳拟合直线和疲劳载荷-疲劳寿命曲线二参数幂函数方程。结果表明:接头静态和疲劳失效形式分别为下板被拉出和下板断裂。铆钉分布结构对接头静强度、变形能力、能量吸收能力、疲劳寿命及它们的稳定性均有影响。m-i接头静力学性能良好,m-o接头整体具有良好的疲劳性能。疲劳测试中,铆钉分布结构会导致首要和次要承载顺序的产生,疲劳断口为首要承载顺序所在位置。
The mechanism of mechanical properties of Self-piercing Riveted (SPR) joints of aluminum alloy 5052 sheet with three rivets was investigated by experiments. The static and fatigue experimental data of m-o SPR joint (m-o joint) and m-I SPR joint (m-I joint) were obtained. The effectiveness of the experimental data was tested by normal distribution and two-parameter Weibull distribution. The best-fitting straight line of fatigue lift and two-parameter power function equations of fatigue load-fatigue life curves were acquired by least square method. Results show that the static fatigue failure modes of the SPR joint are the pull-out and fracture of the lower sheet respectively. The static strength, capacity of deformation and energy absorption, fatigue life and their stability of SPR joints with multiple rivets are all influenced by the distribution structure of the rivets. The m-I joints have favorable static property, but the m-o joints have excellent fatigue property overall. During the fatigue test, the sequences of the primary and secondary load bearing are generated by the distribution structure of rivets, and the fatigue fracture surface is the location of the primary load bearing sequence.
自冲铆技术是近年来迅速发展起来的一种新型连接方法, 因其独特的优势成为最有潜力的替代连接技术[1, 2, 3]。自冲铆采用冲头将一个半空心铆钉压入板材, 刺穿上层板料, 在凹模作用下铆钉管腿在底层板料中翻开形成铆扣, 获得机械内锁结构从而将上板和下板连接在一起。与传统铆接方法相比, 自冲铆可有效连接多层、有镀层的同种或异种材质和厚度的板材及难以采用点焊连接的板材。自动化程度高、易实现批量现代化生产, 且过程在线监控, 无需表面预处理、无需预打孔操作、操作环境安全友好、低能耗。目前一些汽车制造商已开始将自冲铆技术应用于生产中。Calabrese等[4]研究了自冲铆接头在腐蚀环境下的腐蚀特征和静强度。Fu等[5]研究了铆接压力、累积疲劳加载路径和预循环对6111铝合金自冲铆强度的影响。Sun等[6]研究了自冲铆受力状态、上下板厚度组合、材料组合、铆接方向和粘接剂的使用对自冲铆疲劳特性的影响。Hoang等[7]从工艺角度分析铆接过程中预应力和自然时效处理对铝制铆钉自冲铆接头静态特性的影响。He等[8, 9, 10]从铆接质量评估角度采用变差系数法预测自冲铆接头的强度和分析工艺参数的影响。此外, Li等[11, 12]研究了双铆钉自冲铆接头中边缘距离对接头质量、静力学特性和疲劳特性的影响, 其实质为接头的结构优化研究。Hoang等[13]基于铝质铆钉对多铆钉自冲铆部件进行了静力学试验和相应的数值模拟, 主要针对部件整体的特性, 研究了不同加载条件下多颗铝质铆钉连接的T-型自冲铆部件的静力学性能。
目前, 自冲铆的研究主要集中于单铆钉自冲铆接头, 有关多铆钉自冲铆接头的研究较少。现有的多铆钉自冲铆接头的研究目标在于优化接头尺寸[11, 12], 或是研究部件整体的特性[13], 不能很好地说明多铆钉自冲铆接头的力学性能机理。自冲铆疲劳性能的研究中均采用理想的正弦波形的载荷加载方式[5, 6, 12]。为分析多铆钉自冲铆接头承载机理, 考虑到自冲铆连接技术在应用中的工作条件(尤其是汽车和航空器中), 本文以两种铆钉分布结构的3颗铆钉5052铝合金(AA5052)自冲铆接头为对象, 进行静力学和疲劳试验, 疲劳试验中采用三角波形载荷加载, 从而分析多铆钉自冲铆接头的力学性能机理。
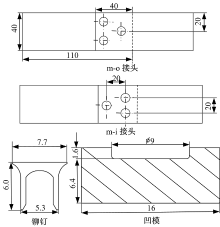
被连接件为2 mm厚的AA5052板材, 相同规格的试样分别为两种接头形式:m-o自冲铆接头(简称m-o接头)和m-i自冲铆接头(m-i接头)。采用Boellhoff公司RIVSET VARIO-FC型自冲铆设备, 铆钉为该公司生产的冷镀锌钢铆钉, 凹模为平底模具。试样、铆钉和凹模几何尺寸如图1所示。铆接过程中采用定位块进行铆接点定位、试铆。观察检验铆接件子午面, 确定铆接参数:预紧压强5 MPa, 铆接压强18 MPa, 整形压强11 MPa。通过载荷-行程曲线在线监控铆接质量, 保证后续试验中试件的可靠性。
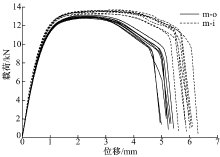
在MTS Landmark 100试验机上进行静力学试验, 两种接头每组各8个试件。选择组件拉伸模块, 拉伸速度为5 mm/min。由于试样承受拉伸剪切载荷, 试验中使用垫片, 避免试验过程中产生扭矩。垫片尺寸为30 mm× 40 mm× 2 mm, 试件有效长度为120 mm。试件组载荷-位移曲线和失效模式分别如图2和图3所示。
由图2可知:各试件组最大载荷及位移数据比较稳定, 选择正态分布来检验数据。使用Matlab拟合优度测试命令检验试件组最大载荷及位移数据是否服从正态分布, 以95%的置信度估计置信区间检验数据的有效性。试件组最大载荷及位移统计量见表1。表1中m-o-F和m-i-F分别表示m-o和m-i接头的最大载荷, m-o-D和m-i-D分别表示它们的最大位移。
| 表1 最大载荷及位移统计量 Table 1 Statistic of maximum load and displacement |
检验结果表明:试件组最大载荷及位移数据服从正态分布, 且试件组数据基本符合各自的置信区间, 即为有效数据。由图2和表1可知:两种接头的静力学性能可重复性和稳定性很高, 为了清晰地对比分析两种接头的特性, 在两种接头中各选择一个最接近均值的试验数据, 如图4所示。以m-o接头为例, 特征化载荷-位移曲线, 曲线被点线大致划分为a、b、c和d四个区域, 曲线与短点线的交点处为m-o接头的最大载荷所在位置。在此定义接头的刚度为载荷与位移的比值, 即为载荷-位移曲线的斜率。
由表1和图4可知:m-i接头静力学性能优于m-o接头。m-i接头平均最大承载能力比m-o接头高4.49%; 虽然两种接头最大载荷稳定性良好且比较接近, 然而m-o接头的稳定性更加突出。m-i接头的平均变形能力比m-o接头高15%; 与最大载荷稳定性特征相似, m-o接头仍然显示出更加良好的稳定性。最大载荷和良好的变形表明m-i接头在失效前可吸收更多的能量。将载荷-位移曲线图片导入AutoCAD软件中实现其横坐标1∶ 1显示, 获得接头载荷-位移曲线与横坐标系所围成区域的面积, 根据以下关系式计算接头的能量吸收值:
式中:Scoordinate为缩放后整个坐标系所围成区域的面积; Wunit为坐标系中横、纵坐标单位刻度所围成面积所代表的能量值; x为曲线与横坐标系所围成区域的面积。
计算表明, m-i接头的缓冲吸震能力比m-o接头高24.95%。
由图4观察可知, 试验开始后很短的时间内(变形量在0.11 mm以内), 区域a中两种接头的载荷发生交叉且刚度呈现出波浪状变化, 这可能是夹具机械调整所致, 此时载荷和刚度不能代表接头的特性。当进入稳定阶段后(区域b), 两种接头的载荷线性上升。m-i接头的最大初始刚度比m-o接头的大3.08%; 随着载荷的增加, 两种接头的刚度均以较快速率下降, 当达到接头最大载荷时, m-o和m-i接头的刚度较其最大初始刚度分别下降170.80%和141.01%。显然, 两种接头在达到最大载荷后载荷均保持了一段时间, 但m-i接头的保持时间更长, 促进了m-i接头变形量的延长。随后, 在区域c中接头载荷和刚度缓慢下降, m-i接头的载荷和刚度下降速率均小于m-o接头。最后, 在阶段d中铆钉与下板之间仅有的局部连接受到破坏, 接头失去承载能力, 载荷急剧下降, 此时两种接头的刚度也迅速降低, 且二者的降低速率几乎相同。这些结果与试验过程中接头的失效机制有关, 通过后续对失效模式的分析进行说明。
通过对试样失效过程和图3中失效模式的观察, 发现两种接头的失效过程和失效模式相似。决定自冲铆接头剪切强度的因素是板材接触面之间的摩擦力和铆钉-板材之间形成的内锁结构力[4], 所以两种接头显示出相似的失效特征:①失效过程中, 上板靠近自由端部的铆钉先失效, 之后内侧的铆钉失效; ②上板靠近自由端部的铆钉从下板中拉出, 铆钉头部轻微下陷; 内侧的铆钉未被完全拉出, 铆钉头部发生严重下陷; 下板内锁结构“ 碗” 边缘发生膨胀, 且“ 碗” 底出现圆周状破裂。
由于连接结构不同又呈现出明显差异, 导致两种接头产生了不同的抗剪切强度、变形量和稳定性。试验初期, 随着变形量的增加, 板材发生弯曲, 接头中上板靠近自由端部的铆钉受到“ 翘曲倾斜” 作用, 其内锁结构被破坏, 之后板材接触面之间的摩擦力和部分内锁结构力提供阻力。根据该变形特征可知, m-o接头最大载荷由上板靠近自由端部的两颗横向铆钉提供, 随后另外的一颗铆钉承载至失效。而m-i接头中上板靠近自由端部的一颗铆钉很快失效, 当内侧两颗横向铆钉承载时达到最大值, 因此提升了塑性变形能力以及延长了位移变形量。由图3可知:m-i接头下板边缘变形程度更大, 还观察到该接头下板两“ 碗” 底处破裂程度不同; 而m-o接头最后阶段的力学性能由一颗铆钉所维持, 因此它具有良好的稳定性。
实际应用中, 机械结构通常承受非稳定载荷(疲劳载荷), 甚至有时工作环境较为苛刻, 而疲劳失效载荷往往远低于静态断裂分析所估算的强度指标, 且失效前宏观上无明显变化, 在疲劳极限状态下突然失效, 造成严重后果。本文基于试件组静力学试验数据研究其疲劳性能。采用MTS试验机进行疲劳试验, 通过载荷控制选用三角波形进行拉-拉加载, 载荷比R=0.1, 加载频率为10 Hz。当接头出现明显的裂纹或循环次数达到200万时停止试验, 各载荷幅值下至少测试3个试件, 最大疲劳载荷幅值分别取m-o和m-i接头静态最大载荷均值的60%、40%和30%, 即为疲劳加载水平3、2和1。对疲劳寿命均值、标准差和相对滑移量均值进行统计分析, 见表2。
| 表2 疲劳寿命和滑移量统计量 Table 2 Statistic of fatigue life and slip value |
概率统计分布中威布尔分布是根据最弱环节模型或串联模型得到的, 适用于材料断裂强度模型的分析。目前其应用也包括可靠性和疲劳寿命模型, 在进行这些模型分析时, 它比指数分布更加灵活。本文采用二参数威布尔分布对疲劳寿命进行分析, 其分布密度函数为:
式中:α 和β 分别为威布尔分布的形状参数和尺度参数。
因疲劳试验试件数较少, 传统统计方法计算繁琐, 且在确定威布尔参数时存在一定困难。本文采用变差系数法(CV)[9, 10, 14]对疲劳寿命进行分析, 获得α 和β 的近似值。
式中:Γ 为伽玛函数。
计算获得不同疲劳载荷水平下疲劳寿命的α 值和对应的β 值见表2。因将失效概率为63.2%的值定义为威布尔尺度参数, 计算所得的β 值均大于各自的寿命均值[14]。可见, 各疲劳寿命均服从二参数威布尔分布, 验证了数据的有效性。
由表2可知:试验过程中接头相对滑移量很小, 其最大值为0.31 mm。可见, 铆钉分布结构对滑移量几乎无影响, 其值主要由疲劳载荷决定。随着载荷的降低, 滑移量降低。试验过程中滑移量具有良好的稳定性, 在接头断裂时该值快速增加。这与裂纹萌生和扩展具有很强的关联性, 在裂纹萌生或进入扩展第II阶段之前, 滑移量保持为一个稳定的数值; 一旦裂纹萌生或进入扩展第II阶段, 滑移量快速增加直到接头断裂。这些与裂纹萌生、扩展有关的信息可通过相对滑移量获得, 最终可有效避免疲劳失效的突然发生。
由于试验数据主要集中于中等寿命区域[15], 采用最小二乘法(LSM)获得的双对数坐标下接头最小二乘直线和由测试数据所组成的最大疲劳载荷-寿命(F-N)曲线如图5所示。计算获得m-o和m-i接头F-N曲线二参数幂函数方程分别为:Nm-o=109.105F-5.005, Nm-i=108.687F-4.531。
由表2可知:随着疲劳载荷降低, 接头疲劳寿命分散性增大。相同载荷水平下, m-i接头疲劳寿命的分散性要小于m-o接头, 这与接头疲劳失效模式有关。图5表明, 当lgF大于0.897 kN时, m-i接头疲劳强度稍高于m-o接头; 当lgF小于0.897 kN时, m-o接头疲劳强度要高于m-i接头, 即整体上m-o接头显示出较高的疲劳强度。
图6为疲劳失效模式。由图可知, 接头疲劳失效模式均为下板断裂, 断口表面均存在黑色物质。m-o接头断裂部位为两颗铆钉所在处, m-i接头为单颗铆钉所在处。m-o接头中上板靠近自由端部的两颗横向铆钉承受疲劳载荷, 与m-i接头相比, 降低了弯曲程度和减缓了应力集中, 因此提高了接头寿命。但是由于m-o接头中两颗横向铆钉对称性因素的存在, 导致了该接头疲劳失效部位的多样性, 如图6中箭头所示。m-i接头疲劳失效发生于单颗铆钉周围, 说明m-i接头具有良好的疲劳寿命稳定性。
铆接过程中, 由于材料流动细化了基板材料的晶粒尺寸, 在裂纹扩展过程中, 裂纹需要穿越更多的晶界, 阻碍了其扩展过程, 因此可提高材料疲劳性能。宏观结构上, 多铆钉共同承载降低了损伤效应, 提高了接头的疲劳强度。不同的分布结构会产生不同的承载次序(首要和次要承载顺序), 导致强度提高的程度各不相同。
由于m-o接头具有良好的疲劳性能, 以它为对象通过机加工获得该接头中一颗铆钉所在位置处的损伤表面, 并将其与该接头的断口损伤表面(两颗铆钉所在位置处)进行比较。结果表明, 疲劳断口中铆钉体上微震磨损区域的面积更大, 程度更加剧烈。证明了首要和次要承载顺序的存在, 且疲劳断口为首要承载顺序所在位置。
借助FEI公司MLA650扫描电子显微镜(SEM), 其配备有EDAX公司X射线能谱仪(EDX), 设置加速电压为20 kV, 对m-o接头中断口和铆钉体表面进行SEM分析和面域元素分析, 结果如图7所示。由图7(a)观察到, 断口处两颗铆钉管腿表面均存在黑色物质, 根据文献[3]可知其为疲劳微震磨损产物, 它有助于定位裂纹萌生部位。可见, 疲劳裂纹主要萌生于铆钉管腿与下板接触部位, 且损伤由铆钉管腿底部向上蔓延。可推测该过程为:初期相对滑移产生的摩擦力使接触部位产生一些材料磨屑, 磨屑的存在增加了该部位的粗糙度进而增大了摩擦力。这些磨屑被压缩的同时又产生新的磨屑, 在疲劳载荷作用下, 该过程循环往复, 最终在该部位发生微震磨损并形成微动第三体, 使损伤区域不断长大。沿下板厚度方向可清晰地观察到疲劳弧线、准解理、疲劳条带、撕裂棱和次级裂纹。随着裂纹扩展至板材边缘, 板材快速断裂失效, 产生缩颈现象和大量韧窝结构, 呈现出延性断裂特征, 这些特征指明了裂纹扩展路径及失效部位。
由图7(b)可知:该面域内Al元素为主要物质成分, 其分布较为集中且位于铆钉管腿边缘偏上, 这也说明该接触部位的微震磨损生长方向朝着铆钉头部的方向。尽管其分布面积不大, 但含量相当高, 可见, 该处发生了剧烈的微震磨损。
根据观察发现, 所有接头疲劳裂纹萌生于铆钉管腿与下板接触部位, 沿下板厚度和宽度方向扩展直至板材边缘。由于铆接后铆钉与下板接触部位存在较大接触应力, 加之疲劳试验中铆钉与下板发生相对滑移, 产生弯曲效应, 疲劳载荷作用下诸如应力强度因子之类的弹性应力集中是裂纹扩展的促进因素[6], 因此该部位成为最薄弱环节。
(1)静态加载下, 接头失效形式均为下板被拉出; 多铆钉接头的静力学性能稳定性良好, 其中m-o接头的稳定性优势更加突出。m-i接头具有较大的静强度、良好的变形能力和较强的能量吸收能力。
(2)疲劳加载下, 接头失效形式均为下板断裂。随着疲劳载荷下降, 接头相对滑移量降低。总体而言, m-o接头疲劳寿命高于m-i接头; 而m-i接头疲劳寿命稳定性优于m-o接头。
(3)疲劳加载下, 接头中铆钉分布结构会导致首要和次要承载顺序的产生, 疲劳断口为首要承载顺序所在位置。铆钉与下板接触部位的相对滑移产生的微震磨损导致并加速了裂纹的萌生; 随后裂纹沿下板厚度和宽度方向扩展, 板材在边缘处快速断裂。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|