电动车用永磁电机新型观测器设计

引用本文

张永博, 易伯瑜, 康龙云. 电动车用永磁电机新型观测器设计. 2015, 45(5): 1527-1534
ZHANG Yong-bo, YI Bo-yu, KANG Long-yun. Novel observer design of permanent magnet synchronous motor for electric vehicles. Journal of Jilin University Engineering and Technology Edition, 2015, 45(5): 1527-1534 复制到剪切板

Permissions

电动车用永磁电机新型观测器设计

张永博^1,², 易伯瑜¹, 康龙云¹

1.华南理工大学机械与汽车工程学院, 广州 510640

2.华南农业大学工程学院广州 510642

康龙云(1961-),男,教授,博士生导师.研究方向:可再生能源,新能源变换控制技术,新能源汽车电机驱动技术.E-mail:lykang@scut.edu.cn

作者简介:张永博(1968-),男,讲师,博士研究生.研究方向:增程式电动车.E-mail:ybzhang@scau.edu.cn

基金:国家自然科学基金项目(51377058)

摘要

在电动汽车永磁同步电机的无传感器控制中,转子磁链值的参数摄动对转子速度和角度的辨识效果影响较大。为此,可以把转子磁链作为变量加入到扩展卡尔曼滤波器中进行辨识,但这会增加运算矩阵的阶数,造成实际系统运算量偏大。为解决这一问题,通过坐标变换的方法将高阶的扩展卡尔曼滤波器分解成为两个并行的低阶卡尔曼滤波器,提出一种用于永磁电机无传感器控制的非线性两段扩展卡尔曼滤波器,并在理论上分析了滤波器所需的乘法加法运算次数。仿真及实验结果表明:与原有传统卡尔曼滤波器相比,该算法减少了一定的运算量并保持了良好的辨识效果。

关键词: 自动控制技术; 无传感器控制; 转子磁链; 非线性两段扩展卡尔曼滤波器

中图分类号:TP29 文献标志码:A 文章编号:1671-5497(2015)05-1527-08

Novel observer design of permanent magnet synchronous motor for electric vehicles

ZHANG Yong-bo^1,², YI Bo-yu¹, KANG Long-yun¹

1.School of Mechanical and Automobile Engineering, South China University of Technology, Guangzhou 510640, China

2.College of Engineering,South China Agriculture University,Guangzhou 510642,China

Abstract

The conventional sensorless algorithm for electric vehicle based on Extended Kalman Filter (EKF) can be influenced by the error of the rotor flux and shows considerable steady-state speed and position deviations. To take rotor flux as a variable in the EKF may increase the order of the operational matrix and the computation load of the real system. To solve this problem and still keep the advantage of the original algorithm, a novel Kalman control strategy using Nonlinear Two-stage EKF (NTSEKF) is proposed. The main idea is to decouple the Kalman filter into two parallel low order filters using coordinate transformation. In theory, the total number of multiplication and addition operations for EKF and NTSEKF is calculated respectively. Simulation and experimental results show that the novel strategy can reduce the number of arithmetic operations compared to EKF meanwhile still keep good identification performance.

Keyword: automatic control technology; sensorless control; rotor flux; nonlinear two-stage extended Kalman filter

Show Figures

0 引言

目前, 交流电机已成为电动汽车的主要动力核心, 其中, 永磁同步电机因功率因数大、功率密度高以及过载能力强等优点而得到广泛应用^{[1, 2]}。传统的永磁同步电机(Permanent magnet synchronous motor, PMSM)检测方法多采用光电编码盘和旋转变压器等设备来测量转子的角度, 这类设备不仅增加了安装及维护成本, 且在高温、潮湿及其他恶劣条件下工作时将降低传感器的可靠性。为了克服机械式传感器带来的缺陷, 使用无传感器技术^{[3, 4]}替代传感器来检测转子磁极的位置, 这种方法也是目前研究的热点之一。

卡尔曼滤波算法^{[5, 6, 7]}是目前常见的无传感器控制方法, 它的实质是对系统的状态向量进行重构, 它以“ 预测-实测-修正” 的顺序递推, 可以从上一采样时刻状态的估计值以及当前状态的测量值消除系统随机干扰, 计算出当前状态的估计量信息, 但为了克服误差扰动的影响, 需要经过大量实验才能确定合适的随机参数。在实际控制中, 转子磁链和定子电感等参数的摄动都对转子速度和角度观测值的准确性有较大的影响, 造成转子参数的观测存在一定误差, 为此国外有学者将这些电机参数作为方程变量加入到卡尔曼滤波器中进行辨识^{[8, 9]}, 以此来提高观测的准确性。但高阶的扩展卡尔曼滤波算法计算量大, 需要较高的硬件配置, 高昂的成本让它无法在工业现场推广使用。为解决这类问题, Hsieh等^[10]提出一种应用于线性系统上的最优两段卡尔曼滤波器(Optimal two-stage Kalman estimator, OTSKE), 该滤波器在本质上是对卡尔曼滤波器(Kalman filter, KF)进行了算法优化, 通过坐标变换的方法将卡尔曼滤波器的计算过程进行了分解, 降低了运算矩阵的阶数, 可以在一定程度上减轻卡尔曼滤波器的计算负担。OTSKE与KF在数学上是完全等价的。进一步深入的研究^{[11, 12, 13, 14]}将这种算法推广使用到非线性系统上, 可以适用于更为普遍的实际情况中。

本文依照OTSKE算法的思路, 提出一种基于非线性两段扩展卡尔曼滤波器(Nonlinear two-stage extended Kalman filter, NTSEKF)的永磁同步电机无传感器算法, 在该算法中, 将一个传统的五阶扩展卡尔曼滤波器分解成四阶卡尔曼滤波器和一阶增广卡尔曼滤波器, 通过两个滤波器的并行协同工作减少了运算量。理论分析和实验结果均显示, 该算法可以有效降低运算量, 从而能够节省系统硬件资源, 降低系统成本。

1 增广卡尔曼滤波器的建模分析

1.1 离散化电机模型的建立

假设磁路不饱和, 空间磁场呈正弦分布, 不计磁滞和涡流损耗影响, 永磁同步电机在两相旋转dq坐标系下的离散状态方程如下^[14]:

$\begin{matrix} \begin{matrix} X [k + 1] = A (Θ) X [k] + \\ B^{u} (Θ) U [k] + B^{Θ} (Θ) Θ [k] (1) \\ Y [k] = C (Θ) X [k] (2) \\ 式中 : \\ \begin{matrix} X (t) & = {[\begin{matrix} i_{d} & i_{q} & ω_{r} & θ_{r} \end{matrix}]}^{T}, Θ = {[ψ_{r}]}^{T}, \\ U & = {[\begin{matrix} u_{α} & u_{β} \end{matrix}]}^{T} \\ A (Θ) & = [\begin{matrix} 1 - \frac{R_{s}}{L_{d}} T_{s} & \frac{ω_{r} L_{q} T_{s}}{L_{d}} & 0 & 0 \\ - \frac{ω_{r} L_{d} T_{s}}{L_{q}} & 1 - \frac{R_{s}}{L_{q}} T_{s} & - \frac{ψ_{r} T_{s}}{L_{q}} & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & T_{s} & 1 \end{matrix}], \\ B^{u} (Θ) & = [\begin{matrix} \frac{\cos θ_{r}}{L_{d}} T_{s} & \frac{\sin θ_{r}}{L_{d}} T_{s} \\ - \frac{si n θ_{r}}{L_{q}} T_{s} & \frac{\cos θ_{r}}{L_{q}} T_{s} \\ 0 & 0 \\ 0 & 0 \end{matrix}], B^{Θ} (Θ) = [\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \end{matrix}], \\ C (Θ) & = [\begin{matrix} \cos θ_{r} & - \sin θ_{r} & 0 & 0 \\ \sin θ_{r} & \cos θ_{r} & 0 & 0 \end{matrix}] \end{matrix} \end{matrix} \end{matrix}$

式中:u_α、u_β为在静止两相坐标系(α β )下的定子电压; i_d、i_q为在旋转两相坐标系(dq)下的定子电流; R_s为定子电阻; R_d为定子d轴电阻; L_d为定子d轴电感; L_q为定子q电感; ψ _r为转子磁链; θ _r为电机的电角度值; ω _r为电机的电角速度值; T_s为采样周期。

1.2 增广卡尔曼滤波器

将转子磁链作为状态变量加入到方程(1)中, 可以写出增广状态方程和输出方程:

$\begin{matrix} \begin{matrix} X [k + 1] = \bar{A} (Θ [k]) X^{a} [k] + \\ \bar{B} (Θ [k]) U [k] + W [k] (3) \\ Y [k] = \bar{C} (Θ) X [k] + B^{y} (Θ [k]) U [k] + η [k] (4) \end{matrix} \end{matrix}$

式中:

$\begin{matrix} \begin{matrix} X^{a} [k] & = [\begin{matrix} X [k] \\ Θ [k] \end{matrix}], \bar{B} (Θ [k]) = [\begin{matrix} B^{u} (Θ [k]) \\ 0 \end{matrix}], \\ \bar{A} (Θ [k]) & = [\begin{matrix} A (Θ [k]) & B^{Θ} (Θ [k]) \\ 0 & G (Θ [k]) \end{matrix}], \\ \bar{C} (Θ) & = [\begin{matrix} C (Θ [k]) & D (Θ [k]) \end{matrix}], \\ W [k] & = [\begin{matrix} W^{x} [k] \\ W^{Θ} [k] \end{matrix}] \end{matrix} \end{matrix}$

W $\begin{matrix} [k] \end{matrix}$ 为过程噪声, η $\begin{matrix} [k] \end{matrix}$ 为测量噪声, 并假定都是零平均白噪声。

基于上述增广状态方程的传统扩展卡尔曼滤波算法如下:

$\begin{matrix} \begin{matrix} X^{a} [k |k - 1] = \bar{A} [k - 1] X^{a} [k - 1 |k - 1] + \\ \bar{B} [k - 1] U [k - 1] (5) \\ P [k |k - 1] = \\ \bar{F} [k - 1] P [k - 1 |k - 1] \bar{F} {[k - 1]}^{T} + Q \\ (6) \\ K [k] = P [k |k - 1] \cdot \\ \bar{H} {[k]}^{T} {(\bar{H} [k] P [k |k - 1] \bar{H} {[k]}^{T} + R)}^{- 1} (7) \\ X^{a} [k |k] = X^{a} [k |k - 1] + \\ K [k] (Y [k] - \bar{H} [k] X^{a} [k |k - 1] - B^{y} [k] U [k]) (8) \\ P [k |k] = P [k |k - 1] - K [k] \bar{H} [k] P [k |k - 1] (9) \end{matrix} \end{matrix}$

式中:

$\begin{matrix} \bar{F} \end{matrix} \begin{matrix} [k] \end{matrix}$ = $\begin{matrix} [\begin{matrix} F (Θ [k]) & E (Θ [k]) \\ 0 & G (Θ [k]) \end{matrix}] \end{matrix}$ ,

$\begin{matrix} \bar{H} \end{matrix} \begin{matrix} [k] \end{matrix}$ = $\begin{matrix} [\begin{matrix} H_{1} (Θ [k]) & H_{2} (Θ [k]) \end{matrix}] \end{matrix}$ ,

K $\begin{matrix} [k] \end{matrix}$ = $\begin{matrix} [\begin{matrix} K^{x} [k] \\ K^{Θ} [k] \end{matrix}] \end{matrix}$ ,

F $\begin{matrix} (Θ [k]) \end{matrix}$ = $\begin{matrix} \frac{\partial}{\partial X} \end{matrix}$ {A $\begin{matrix} (Θ [k]) \end{matrix}$ X $\begin{matrix} [k] \end{matrix}$ +

B^u $\begin{matrix} (Θ [k]) \end{matrix}$ U $\begin{matrix} [k] \end{matrix}$ +B^Θ $\begin{matrix} (Θ [k]) \end{matrix}$ Θ $\begin{matrix} [k] \end{matrix}$ },

F $\begin{matrix} (Θ [k]) \end{matrix}$ =

$\begin{matrix} [\begin{matrix} 1 - \frac{R_{s}}{L_{d}} T_{s} & \frac{ω_{r} L_{q} T_{s}}{L_{d}} & \frac{I_{q} L_{q} T_{s}}{L_{d}} & \frac{U_{q} T_{s}}{L_{d}} \\ - \frac{ω_{r} L_{d} T_{s}}{L_{q}} & 1 - \frac{R_{s}}{L_{q}} T_{s} & - \frac{I_{d} L_{d} T_{s}}{L_{q}} - \frac{ψ_{r} T_{s}}{L_{q}} & - \frac{U_{d} T_{s}}{L_{q}} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & T_{s} & 1 \end{matrix}] \end{matrix}$ ,

E $\begin{matrix} (Θ [k]) \end{matrix}$ = $\begin{matrix} \frac{\partial}{\partial Θ} \end{matrix}$ {A $\begin{matrix} (Θ [k]) \end{matrix}$ X $\begin{matrix} [k] \end{matrix}$ +

B^u $\begin{matrix} (Θ [k]) \end{matrix}$ U $\begin{matrix} [k] \end{matrix}$ +B^Θ $\begin{matrix} (Θ [k]) \end{matrix}$ Θ $\begin{matrix} [k] \end{matrix}$ },

E $\begin{matrix} (Θ [k]) \end{matrix}$ = $\begin{matrix} {[\begin{matrix} 0 & - \frac{ω_{r} T_{s}}{L_{q}} & 0 & 0 \end{matrix}]}^{T} \end{matrix}$ ,

G $\begin{matrix} (Θ [k]) \end{matrix}$ = $\begin{matrix} [1] \end{matrix}$ ,

D $\begin{matrix} (Θ [k]) \end{matrix}$ = $\begin{matrix} {[\begin{matrix} 0 & 0 \end{matrix}]}^{T} \end{matrix}$ ,

H₁ $\begin{matrix} (Θ [k]) \end{matrix}$ = $\begin{matrix} \frac{\partial}{\partial X} \end{matrix}$ {C $\begin{matrix} (Θ [k]) \end{matrix}$ X $\begin{matrix} [k] \end{matrix}$ +

B^y $\begin{matrix} (Θ [k]) \end{matrix}$ U $\begin{matrix} [k] \end{matrix}$ +D $\begin{matrix} (Θ [k]) \end{matrix}$ Θ $\begin{matrix} [k] \end{matrix}$ },

H₁ $\begin{matrix} (Θ [k]) \end{matrix}$ =

$\begin{matrix} [\begin{matrix} \cos θ_{r} & - \sin θ_{r} & 0 & - I_{d} \sin θ_{r} - I_{q} \cos θ_{r} \\ \sin θ_{r} & \cos θ_{r} & 0 & I_{d} \cos θ_{r} - I_{q} \sin θ_{r} \end{matrix}] \end{matrix}$

H₂ $\begin{matrix} (Θ [k]) \end{matrix}$ = $\begin{matrix} \frac{\partial}{\partial Θ} \end{matrix}$ {C $\begin{matrix} (Θ [k]) \end{matrix}$ X $\begin{matrix} [k] \end{matrix}$ +

B^y $\begin{matrix} (Θ [k]) \end{matrix}$ U $\begin{matrix} [k] \end{matrix}$ +D $\begin{matrix} (Θ [k]) \end{matrix}$ Θ $\begin{matrix} [k] \end{matrix}$ },

H₂ $\begin{matrix} (Θ [k]) \end{matrix}$ = $\begin{matrix} [\begin{matrix} 0 & 0 \end{matrix}] \end{matrix}$ ,

P $\begin{matrix} (\cdot) \end{matrix}$ = $\begin{matrix} [\begin{matrix} P^{x} [\cdot] & P^{xΘ} [\cdot] \\ P^{xΘ} {[\cdot]}^{T} & P^{Θ} [\cdot] \end{matrix}] \end{matrix}$

2 非线性两段卡尔曼滤波器的算法

为了实现NTSEKF算法, 将引入坐标变换矩阵T $\begin{matrix} [\cdot] \end{matrix}$ :

$\begin{matrix} T (J) = [\begin{matrix} I & J \\ 0 & I \end{matrix}] (10) \end{matrix}$

通过相应的坐标变换后, 将方差-协方差矩阵P $\begin{matrix} [\cdot] \end{matrix}$ 变换成式(11)所示对角矩阵 $\begin{matrix} \bar{P} \end{matrix} \begin{matrix} [\cdot] \end{matrix}$ :

$\begin{matrix} \bar{P} [\cdot] = [\begin{matrix} {\bar{P}}^{x} [\cdot] & 0 \\ 0 & {\bar{P}}^{Θ} [\cdot] \end{matrix}] (11) \end{matrix}$

基于T $\begin{matrix} [\cdot] \end{matrix}$ 的形式定义两个变换矩阵T $\begin{matrix} (M [k]) \end{matrix}$ 和T $\begin{matrix} (N [k]) \end{matrix}$ , M $\begin{matrix} [k] \end{matrix}$ 和N $\begin{matrix} [k] \end{matrix}$ 分别被定义为:

$\begin{matrix} \begin{matrix} M [k] = P^{xΘ} [k |k - 1] {(P^{Θ} [k |k - 1])}^{- 1} \\ N [k] = P^{xΘ} [k |k] {(P^{Θ} [k |k])}^{- 1} \end{matrix} \end{matrix}$

利用这两个矩阵可以进行如下变换:

$\begin{matrix} \{\begin{matrix} X^{a} [k |k - 1] = T (M [k]) {\bar{X}}^{a} [k |k - 1] \\ P [k |k - 1] = T (M [k]) \bar{P} [k |k - \\ 1] T {(M [k])}^{T} \\ X^{a} [k |k] = T (N [k]) {\bar{X}}^{a} [k |k] \\ K [k] = T (N [k]) \bar{K} [k] \\ P [k |k] = T (N [k]) \bar{P} [k |k] T {(N [k])}^{T} \end{matrix} (12) \end{matrix}$

通过进行矩阵变换, 并将其代入到扩展卡尔曼滤波方程(5)~(9)中, 根据一一对应关系^[12], 就可以得到NTSEKF算法的第一阶段状态参数预测方程组如下:

$\begin{matrix} \begin{matrix} {\bar{P}}^{Θ} [k |k - 1] = G [k - 1] {\bar{P}}^{Θ} [k - 1 |k - 1] \cdot \\ G {[k - 1]}^{T} + Q^{Θ} [k] (13) \\ E [k] = \frac{\partial}{\partial Θ} {A [k] (\bar{X} [k] + N [k] \bar{Θ} [k]) + \\ B^{Θ} [k] Θ [k] + B^{u} [k] U [k]} |_{_{\bar{Θ} [k |k]}} (14) \\ \bar{M} [k] = {F [k - 1] N [k - 1] + \\ E [k - 1] |_{Θ [k - 1 |k - 1]}} {(G [k - 1])}^{- 1} (15) \\ M [k] = \bar{M} [k] + (Q^{xΘ} [k] - \\ \bar{M} [k] Q^{Θ} [k]) {\bar{P}}^{Θ} {[k |k - 1]}^{- 1} (16) \\ {\bar{Q}}^{x} [k] = Q^{x} [k] - Q^{xΘ} [k] \bar{M} {[k]}^{T} - \\ M [k] {Q^{xΘ} [k] - \bar{M} [k] Q^{Θ} {[k]}}^{T} (17) \\ {\bar{P}}^{x} [k |k - 1] = F [k - 1] {\bar{P}}^{x} [k - 1 |k - 1] \cdot \\ F {[k - 1]}^{T} + {\bar{Q}}^{x} [k] (18) \\ \bar{Θ} [k |k - 1] = G [k - 1] \bar{Θ} [k - 1 |k - 1] (19) \\ u [k - 1] = {A [k - 1] N [k - 1] + \\ B^{Θ} [k - 1] M [k] G [k - 1]} \cdot \\ \bar{Θ} [k - 1 |k - 1] (20) \\ \bar{X} [k |k - 1] = A [k - 1] \bar{X} [k - 1 |k - 1] + \\ B^{u} [k - 1] U [k - 1] + u [k - 1] (21) \end{matrix} \end{matrix}$

NTSEKF算法第二阶段的状态参数更新方程如下:

$\begin{matrix} \begin{matrix} \bar{S} [k] = C [k] M [k] + D [k] (22) \\ S [k] = H_{1} [k] M [k] + H_{2} [k] (23) \\ {\bar{K}}^{Θ} [k] = {\bar{P}}^{Θ} [k |k - 1] S {[k]}^{T} \cdot \\ {H_{1} [k] {\bar{P}}^{x} [k |k - 1] H_{1} {[k]}^{T} + R [k] + \\ S [k] {\bar{P}}^{Θ} [k |k - 1] S {[k]}^{T}}^{- 1} (24) \\ {\bar{P}}^{Θ} [k |k] = {\bar{P}}^{Θ} [k |k - 1] - \\ {\bar{K}}^{Θ} [k] S [k] {\bar{P}}^{Θ} [k |k - 1] (25) \\ \bar{Θ} [k |k] = \bar{Θ} [k |k - 1] + \\ {\bar{K}}^{Θ} [k] (Y [k] - C [k] \bar{X} [k |k - 1] - \\ \bar{S} [k] \bar{Θ} [k |k - 1] - B^{y} [k] U [k]) (26) \\ {\bar{K}}^{x} [k] = {\bar{P}}^{x} [k |k - 1] H_{1} {[k]}^{T} \\ {H_{1} [k] {\bar{P}}^{x} [k |k - 1] H_{1} {[k] + R}}^{- 1} \\ (27) \\ {\bar{P}}^{x} [k |k] = {\bar{P}}^{x} [k |k - 1] - \\ {\bar{K}}^{x} [k] H_{1} [k] {\bar{P}}^{x} [k |k - 1] (28) \\ \bar{X} [k |k] = \bar{X} [k |k - 1] + \\ {\bar{K}}^{x} [k] {Y [k] - C [k] \bar{X} [k |k - 1] - \\ (S - \bar{S}) \bar{Θ} [k |k - 1] - B^{y} [k] U [k]} \\ (29) \\ \hat{X} [k |k - 1] = \bar{X} [k |k - 1] + \\ M [k] \bar{Θ} [k |k - 1] (30) \\ \hat{X} [k |k] = \bar{X} [k |k] + N [k] \bar{Θ} [k |k] (31) \end{matrix} \end{matrix}$

式中:N $\begin{matrix} [k] \end{matrix}$ =M $\begin{matrix} [k] \end{matrix}$ - $\begin{matrix} {\bar{K}}^{x} \end{matrix} \begin{matrix} [k] \end{matrix}$ S $\begin{matrix} [k] \end{matrix}$ 。

非线性NTSEKF的初始条件需使用传统EKF的初始状态( $\begin{matrix} \hat{X} \end{matrix} \begin{matrix} [0 |0] \end{matrix}$ , $\begin{matrix} \hat{Θ} \end{matrix} \begin{matrix} [0 |0] \end{matrix}$ , P^x $\begin{matrix} [0 |0] \end{matrix}$ , P^Θ $\begin{matrix} [0 |0] \end{matrix}$ , P^xΘ $\begin{matrix} [0 |0] \end{matrix}$ ), 利用对应的关系可得NTSEKF的初始值:

$\begin{matrix} \begin{matrix} N [0] = P^{xΘ} [0 |0] {(P^{Θ} [0 |0])}^{- 1} (32) \\ X [0 |0] = \hat{X} [0 |0] - N [0] \bar{Θ} [0 |0] (33) \\ \bar{Θ} [0 |0] = \hat{Θ} [0 |0] (34) \\ P^{x} [0 |0] = P^{x} [0 |0] - N [0] P^{Θ} [0 |0] N {[0]}^{T} (35) \\ {\bar{P}}^{Θ} [0 |0] = P^{Θ} [0 |0] (36) \end{matrix} \end{matrix}$

3 运算量的理论分析

为了体现出算法的优势, 对两组滤波器的运算量进行了理论分析, 由于滤波器的运算是通过加法和乘法来实现的, 所以用加法和乘法的运算次数来衡量算法的运算量。例如, 对传统的扩展卡尔曼滤波器方程P[k $\begin{matrix} |k - 1 \end{matrix}$ ]= $\begin{matrix} \bar{F} \end{matrix}$ [k-1]P[k-1 $\begin{matrix} |k - 1 \end{matrix}$ ] $\begin{matrix} \bar{F} \end{matrix}$ [k-1]^T+Q进行运算, 假设矩阵F, P, Q的阶数n均为5, 为了计算出P $\begin{matrix} [k |k - 1] \end{matrix}$ , 所需的乘法运算次数为2n³=250次, 所需的加法运算次数为2n³-n²=225次, 其他的以此类推。

基于经典扩展卡尔曼滤波器方程组, 可以得出理论上的运算量, 如表1所示。其中, n=5, 为状态量维数; m=2, 为输出维数; q=2, 为输入维数。

根据NTSEKF算法, 可得理论上的运算量如表2所示, 其中q=2, 为观测量维数; n=4, m=2, p=1。

表1 扩展卡尔曼滤波器算法运算量统计表 Table 1 EKF arithmetic operation requirement

统计量	乘法运算数量	加法运算数量
系数矩阵	12次	2次
u_d和u_q	4次	2次
X^a $\begin{matrix} [k \|k - 1] \end{matrix}$	n²+nq(35次)	n²-n+nq(30次)
P $\begin{matrix} [k \|k - 1] \end{matrix}$	2n³(250次)	2n³-n²(225次)
X^a $\begin{matrix} [k \|k] \end{matrix}$	2nm+mq(24次)	2nm+mq(24次)
K $\begin{matrix} [k] \end{matrix}$	n²m+2nm²+m³ (98次)	n²m+2nm²+m³-2nm (78次)
P $\begin{matrix} [k \|k] \end{matrix}$	n²m+n³(175次)	n²m+n³-n²(150次)
总计	598次	511次

表1 扩展卡尔曼滤波器算法运算量统计表 Table 1 EKF arithmetic operation requirement

表2 NTSEKF算法运算量统计表 Table 2 NTSEKF arithmetic operation requirement

统计量	乘法运算数量	加法运算数量
系数矩阵AX(Θ ), B^u(Θ ), B^Θ(Θ ), H	24次	4次
u_d和u_q	4次	2次
$\begin{matrix} \bar{X} \end{matrix} \begin{matrix} [k \|k - 1] \end{matrix}$	n²+nq(24次)	n²+nq(24次)
u $\begin{matrix} [k - 1] \end{matrix}$	n²p+np²+np (24次)	n²p+np²-np+ 2p²-p(17次)
$\begin{matrix} {\bar{P}}^{x} \end{matrix} \begin{matrix} [k \|k - 1] \end{matrix}$	2n³(128次)	2n³-n²(112次)
$\begin{matrix} {\bar{Q}}^{x} \end{matrix} \begin{matrix} [k - 1] \end{matrix}$	2n²p(32次)	2n²p(32次)
$\begin{matrix} \bar{M} \end{matrix} \begin{matrix} [k - 1] \end{matrix}$	n²p+np²+p³ (21次)	n²p+np²+p³- np(17次)
M $\begin{matrix} [k - 1] \end{matrix}$	2n²p+p³(33次)	2n²p+p³(33次)
$\begin{matrix} \bar{Θ} \end{matrix} \begin{matrix} [k \|k - 1] \end{matrix}$	p²(1次)	p²-p(0次)
$\begin{matrix} {\bar{P}}^{Θ} \end{matrix} \begin{matrix} [k \|k - 1] \end{matrix}$	2p³(2次)	2p³-p²(1次)
$\begin{matrix} \bar{X} \end{matrix} \begin{matrix} [k \|k] \end{matrix}$	nm+mp(10次)	nm+mp(10次)
$\begin{matrix} {\bar{K}}^{x} \end{matrix} \begin{matrix} [k \|k] \end{matrix}$	n²m+2nm²+ m³(72次)	n²m+2nm²+m³- 2nm(56次)
$\begin{matrix} {\bar{P}}^{x} \end{matrix} \begin{matrix} [k \|k] \end{matrix}$	n²m+n³(96次)	n²m+n³-n²(80次)
$\begin{matrix} \bar{Θ} \end{matrix} \begin{matrix} [k \|k] \end{matrix}$	2mp+nm+mq (16次)	2mp+nm+mq (16次)
$\begin{matrix} {\bar{K}}^{Θ} \end{matrix} \begin{matrix} [k \|k] \end{matrix}$	2p²m+2pm²+m³ (20次)	2p²m+3pm²+ m³-3pm(18次)
$\begin{matrix} {\bar{P}}^{Θ} \end{matrix} \begin{matrix} [k \|k] \end{matrix}$	p²m(2次)	p²m(2次)
S $\begin{matrix} [k] \end{matrix}$	npm(8次)	mp(2次)
$\begin{matrix} \bar{S} \end{matrix} \begin{matrix} [k] \end{matrix}$	npm(8次)	mp(2次)
N $\begin{matrix} [k] \end{matrix}$	npm(8次)	np(4次)
总计	533次	432次

表2 NTSEKF算法运算量统计表 Table 2 NTSEKF arithmetic operation requirement

4 仿真实验

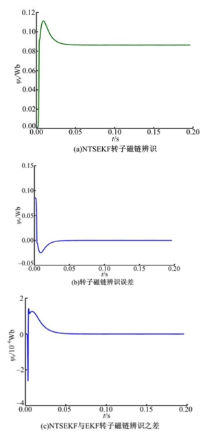
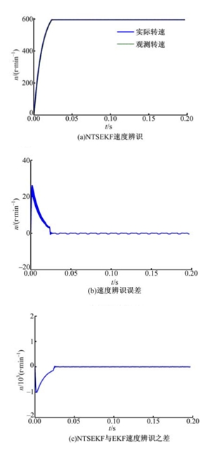
为了验证基于NTSEKF无传感器算法的有效性, 采用MATLAB/Simulink软件对系统进行了仿真研究。永磁同步电机的仿真参数如下:额定功率P_N=1.2 kW, 额定线电压U_N=300 V, 额定频率f_N=50 Hz, 定子电阻R_s=0.525 Ω , d轴电感L_d=1.65 mH, q轴电感L_q=1.65 mH, 转子磁链值ψ _r=0.08627 Wb, 极对数P=4, 额定转速n_N=3000 r/min。设定负载为2 N· m, 速度变化设定为600 r/min, 同时, 为了检验NTSEKF算法的和传统的扩展卡尔曼滤波器在算法上的等价性, 将两组滤波器加入到同一仿真模型中。其中, 传统的两段滤波器辨识出的电机参数参与电机的无传感器闭环控制, 扩展卡尔曼滤波器只根据电机的电流电压参数进行辨识, 所得结果不参与控制。图1、图2和图3分别是NTSEKF对转子磁链、转速以及转子电角度值的观测值、观测误差以及与EKF观测值之差。从仿真图上可以看出:NTSEKF参数辨识效果良好, 在初始阶段, 误差快速增大, 在达到最大值后, 误差逐渐减小, 在转速到达额定值后, 各项观测值都收敛到真实值。而NTSEKF与EKF的观测值之差极小, 这是由于NTSEKF的计算步骤多于EKF, 在计算过程中造成的精度损失完全可以忽略不计。

	Figure Option View Download New Window
	图1 转子磁链辨识仿真波形Fig.1 Simulation waves of rotor flux estimation

	Figure Option View Download New Window
	图2 速度辨识仿真波形Fig.2 Simulation waves of Speed estimation

	Figure Option View Download New Window
	图3 电角度辨识仿真波形Fig.3 Simulation waves of electrical angle estimation

5 实验结果

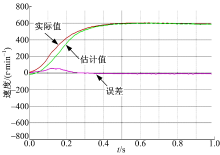
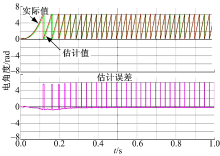
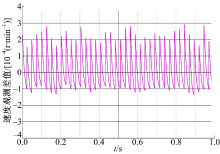
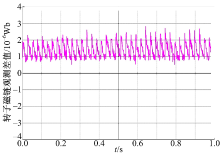
实验中采用Myway公司生产的Expert3系统进行实验, Expert3系统控制器的核心为TI公司的TMS320C6713高性能DSP控制芯片和Xilinx公司型号为SPARTAN-XC3S1500的FPGA, C6713负责核心算法计算, FPGA负责采样信号、产生脉宽调制(PWM)信号等。实验系统中采用一台表面贴式永磁同步电机, 电机参数与仿真所用参数一致。电机负载采用磁粉制动器, 制动器能提供恒定力矩, 且力矩与励磁电流呈线性关系。综合考虑运算精度和DSP的运算能力, 本实验中将逆变器开关频率设为10 kHz, 死区时间设为4 μ s。电机采用多摩川2500线的增量编码器来读取转子的真实位置, 作为估算转子位置的参考。在实际实验中, 负载值设为2 Nm, 速度设定为600 r/min。图4和图5分别是实验中NTSEKF对转速、转子角度值的观测值以及与真实参数之间的误差值。可以看出, NTSEKF对实际参数跟踪效果良好, 稳态误差很小。图6中的转子磁链观测值在经过短暂的超调后迅速稳定。由于转子磁链对电角度的辨识的影响较大, 电角度良好的辨识效果保证了该结果的准确性。图7、图8和图9是两组滤波器输出的转速、转子角度值及转子磁链值之差, 实验结果表明它们的输出相差极小, 与理论推导及仿真结果保持了很好的一致性。这就验证了两组滤波器在数学上是完全等价的。

	Figure Option View Download New Window
	图4 NTSEKF转速辨识Fig.4 Speed estimation based on NTSEKF

	Figure Option View Download New Window
	图5 NTSEKF电角度辨识Fig.5 Electrical angle estimation based on NTSEKF

	Figure Option View Download New Window
	图6 NTSEKF转子磁链辨识Fig.6 Rotor flux estimation based on NTSEKF

	Figure Option View Download New Window
	图7 NTSEKF与EKF转速辨识之差Fig.7 Difference of speed estimation between NTSEKF and EKF

	Figure Option View Download New Window
	图8 NTSEKF与EKF电角度辨识之差Fig.8 Difference of electrical angle estimation between NTSEKF and EKF

	Figure Option View Download New Window
	图9 NTSEKF与EKF转子磁链辨识之差Fig.9 Difference of rotor flux estimation between NTSEKF and EKF

为了在运算量方面有一个直观的比较, 利用DSP自带定时器分别计算传统EKF模块和NTSEKF模块的实际运行时间。定时器计算出传统卡尔曼滤波器的运行时间为71.5438 μ s, 两段卡尔曼滤波器的运行时间为62.7046 μ s, 比传统卡尔曼算法节省了12.355%的运算时间, 与理论的推导基本符合。

6 结束语

为克服无传感器算法中电机参数摄动对辨识结果的影响, 本文在两相旋转坐标系数学模型基础上将转子磁链值加入到辨识变量中, 利用OTSKE算法提出一种新的无传感器NTSEKF算法, 该算法能有效节省运算量并保持良好的辨识结果。仿真及实验结果验证了理论分析的准确性。NTSEKF滤波器的降阶及算法简化对卡尔曼滤波器在电机无传感器控制领域的应用有着积极的意义。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	邹继斌, 李建军, 徐永向, 等. 基于重复控制深海柱塞泵用永磁同步电机转速波动的抑制[J]. 电工技术学报, 2011, 26(6): 46-50. Zou Ji-bin, Li Jian-jun, Xu Yong-xiang, et al. Repetitive controller for suppression of the speed fluctuation in PMSM used for deep-sea plunger pump[J]. Transactions of China Electrotechnical Society, 2011, 26(6): 46-50. [本文引用:1]
[2]	郭新华, 王永兴, 赵峰, 等. 基于SHEPWM的中压大功率牵引永磁同步电机两电平控制[J]. 电工技术学报, 2012, 27(11): 76-82. Guo Xin-hua, Wang Yong-xing, Zhao Feng, et al. Two level control technology of PMSM used in medium voltage high power traction system based on SHEPWM[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 76-82. [本文引用:1]
[3]	鲁文其, 黄文新, 胡育文. 永磁同步电动机新型滑模观测器无传感器控制[J]. 控制理论与应用, 2009, 26(4): 429-432. Lu Wen-qi, Huang Wen-xin, Hu Yu-wen. A novel sliding-mode observer for the sensorless control of permanent-magnet synchronous machines[J]. Control Theory & Applications, 2009, 26(4): 429-432. [本文引用:1]
[4]	王礼鹏, 张化光, 刘秀翀. 永磁同步电动机无速度传感器矢量调速系统的积分反步控制[J]. 控制理论与应用, 2012, 29(2): 199-204. Wang Li-peng, Zhang Hua-guang, Liu Xiu-chong. Integral backstepping controller in the sensorless vector-control system for permanent magnet synchronous motor[J]. Control Theory & Applications, 2012, 29(2): 199-204. [本文引用:1]
[5]	张猛, 肖曦, 李永东. 基于扩展卡尔曼滤波器的永磁同步电机转速和磁链观测器[J]. 中国电机工程学报, 2007, 27(36): 36-40. Zhang Meng, Xiao Xi, Li Yong-dong. Speed and flux linkage observer for permanent magnet synchronous motor based on EKF[J]. Proceedings of the CSEE 2007, 27(36): 36-40. [本文引用:1]
[6]	尹忠刚, 张瑞峰, 钟彦儒, 等. 基于抗差扩展卡尔曼滤波器的永磁同步电机转速估计策略[J]. 控制理论与应用, 2012, 29(7): 921-927. Yin Zhong-gang, Zhang Rui-feng, Zhong Yan-ru, et al. Speed estimation for permanent magnet synchronous motor based on robust extended Kalman filter[J]. Control Theory & Applications, 2012, 29(7): 921-927. [本文引用:1]
[7]	陈振, 刘向东, 靳永强, 等. 采用扩展卡尔曼滤波磁链观测器的永磁同步电机直接转矩控制[J]. 中国电机工程学报, 2008, 28(33): 75-81. Chen Zhen, Liu Xiang-dong, Jin Yong-qiang, et al. Direct torque control of permanent magnet synchronous motors based on extended Kalman filter observer of flux linkage[J]. Proceedings of the CSEE, 2008, 28(33): 75-81. [本文引用:1]
[8]	Vyncke T J, Boel R K, Melkebeek J A A. A comparison of stator flux linkage estimators for a direct torque controlled PMSM drive[C]∥35th Annual Conference of the IEEE Industrial Electronics Society. Porto, Portugal: IEEE, 2009: 971-978. [本文引用:1]
[9]	Vyncke T J, Boel R K, Melkebeek J A A. On the stator flux linkage estimation of an PMSM with extended Kalman filters[C]∥5th IET International Conference on Power Electronics, Machines and Drives. Brighton, United Kingdom: IET, 2010: 1-6. [本文引用:1]
[10]	Hsieh C S, Chen F C. Optimal solution of the two-stage Kalman estimator[J]. IEEE Transactions on Automatic Control, 1999, 44(1): 194-199. [本文引用:1]
[11]	Hsieh C S, Chen F C. Optimal minimal-order least-squares estimators via the general two-stage Kalman filter[J]. IEEE Transactions on Automatic Control, 2001, 46(11): 1772-1776. [本文引用:1]
[12]	Hsieh C S, Chen F C. General two-stage Kalman filters[J]. IEEE Transactions on Automatic Control, 2000, 45(4): 819-824. [本文引用:2]
[13]	Kim K H, Lee J G, Park C G. Adaptive two-stage Kalman filter in the presence of unknown rand om bias[J]. International Journal of Adaptive Control and Signal Processing, 2006, 20(7): 305-319. [本文引用:1]
[14]	Hilairet M, Auger F, Berthelot E. Speed and rotor flux estimation of induction machines using a two-stage extended Kalman filter[J]. Automatica, 2009, 45(8): 1819-1827. [本文引用:2]

2011

0.0

. 2011, 26(6):46-50

Repetitive controller for suppression of the speed fluctuation in PMSM used for deep-sea plunger pump

基于重复控制深海柱塞泵用永磁同步电机转速波动的抑制

Zou Ji-bin , Li Jian-jun , Xu Yong-xiang

邹继斌, 李建军, 徐永向

The characteristic of the periodical torque ripple in deep-sea plunger pump was analyzed, and the influence of the periodical torque ripple on the speed fluctuation under conventional open-loop or closed-loop control is also studied in this paper. It is shown that the conventional PI controller in closed-loop system could not suppress the load disturbance of middle frequency. Considering the periodical character of the relationship between the load disturbance and the rotor position of the rotating motor, the improved repetitive controller is used to decrease the speed fluctuation in low speed. Both the simulated and experimental result show that repetitive control could suppress the periodical speed fluctuation effectively.

结合深海柱塞泵的工作原理, 分析了其负载转矩周期波动的特性, 并在常规转速开闭环控制系统下, 研究了周期性负载扰动对电机输出转速的影响, 指出基于常规PI控制的闭环系统不能抑制中频段的负载扰动。针对负载转矩扰动与电机转动位置相关的周期性特点, 提出采用改进重复控制的策略来抑制电机低速时的转速波动。仿真和实验结果均表明, 重复控制系统能够很好地抑制周期性的转速波动。

... 0 引言目前,交流电机已成为电动汽车的主要动力核心,其中,永磁同步电机因功率因数大、功率密度高以及过载能力强等优点而得到广泛应用^[1,2] ...

2012

0.0

. 2012, 27(11):76-82

Two level control technology of PMSM used in medium voltage high power traction system based on SHEPWM

基于SHEPWM的中压大功率牵引永磁同步电机两电平控制

Guo Xin-hua , Wang Yong-xing , Zhao Feng

郭新华, 王永兴, 赵峰

永磁同步电机具有结构紧凑、高功率密度、高气隙磁通和高转矩惯性比等优点,在中高压牵引驱动领域具有广阔的市场应用前景。本文对基于SHEPWM的中压大功率牵引永磁同步电机的两电平闭环控制技术进行研究,提出了非方波模式时的系统控制策略。研究了该控制策略中三相电压时间域的角度值和电压矢量空间位置角的关系,SHEPWM 的工程实现方法和不同PWM 模式下的动态切换方法等关键技术。经过试验验证,该控制策略达到了预期的消谐要求,动态切换过程中电流平滑,全速度范围内,d、q 电流跟踪良好。

... 0 引言目前,交流电机已成为电动汽车的主要动力核心,其中,永磁同步电机因功率因数大、功率密度高以及过载能力强等优点而得到广泛应用^[1,2] ...

2009

0.0

. 2009, 26(4):429-432 DOI:doi:10.3969/j.issn.1004-7018.2013.03.013

A novel sliding-mode observer for the sensorless control of permanent-magnet synchronous machines

永磁同步电动机新型滑模观测器无传感器控制

Lu Wen-qi , Huang Wen-xin , Hu Yu-wen.

鲁文其, 黄文新, 胡育文

根据滑模变结构控制理论以及永磁同步电动机的数学模型,在传统滑模观测器的基础上,设计了一种将反电势估算值反馈引入到定子电流观测计算中的新型滑模观测器,利用该观测器对永磁同步电动机的转子位置和转速进行了实时在线估算.针对采用滑模控制导致系统出现的抖振现象以及加上其他干扰引起转速计算精度不高的问题,采用了将传统的开关函数更换为近似饱和函数以及锁相环代替直接微分计算转速的方法,有效地抑制了抖振问题,提高了估算精度.仿真实验验证了该新型滑模观测器的正确性和有效性.

... 为了克服机械式传感器带来的缺陷,使用无传感器技术^[3,4]替代传感器来检测转子磁极的位置,这种方法也是目前研究的热点之一 ...

2012

0.0

. 2012, 29(2):199-204

Integral backstepping controller in the sensorless vector-control system for permanent magnet synchronous motor

永磁同步电动机无速度传感器矢量调速系统的积分反步控制

Wang Li-peng , Zhang Hua-guang , Liu Xiu-chong.

王礼鹏, 张化光, 刘秀翀

A robust control system composing of an integral backstepping controller and a sliding-mode variablestructure model-reference adaptive system (MRAS) is designed for the vector-controlled permanent magnet synchronous motor (PMSM). The backstepping control with integral action is employed as the speed and current controllers for the PMSM. The sliding-mode variable-structure MRAS is taken to estimate the speed/position of the drive system. The stability of the speed controller and the estimator is proved by using Lyapunov theorem. MATLAB simulation results validate the good speed-tracking and disturbance-rejection performances of the designed method.

... 为了克服机械式传感器带来的缺陷,使用无传感器技术^[3,4]替代传感器来检测转子磁极的位置,这种方法也是目前研究的热点之一 ...

2007

0.0

. 2007, 27(36):36-40 DOI:doi:10.3321/j.issn:0258-8013.2007.36.007

Speed and flux linkage observer for permanent magnet synchronous motor based on EKF

基于扩展卡尔曼滤波器的永磁同步电机转速和磁链观测器

Zhang Meng , Xiao Xi , Li Yong-dong.

张猛, 肖曦, 李永东

To eliminate the mechanical sensors of permanent magnet synchronous motor (PMSM) drive and get the stator flux linkage used in direct torque control (DTC), an extended Kalman filter (EKF) is established. The stator flux linkage on the fixed a-b coordinate, rotor speed and position are chosen as state variables. The input and output of the EKF are stator voltages and currents. The stator flux linkage and rotor speed are observed by EKF. DTC using space vector modulation (SVM) is applied to the system in order to reduce the torque ripples and keep constant switching frequency. The experimental test is carried out to verify the efficiency and robustness of the proposed sensor-less DTC system with speed and flux linkage observer.

为了取消永磁同步电机控制中的机械传感器，获得直接转矩控制中需要的电机磁链信息，设计了一种基于扩展卡尔曼滤波器的永磁同步电机转速和磁链估算方法。选取定子固定坐标系下定子磁链、电机转速和转子位置为状态变量，电压和电流作为输入、输出量，建立估算定子磁链、电机转速和转子位置的EKF滤波器系统。采用空间矢量调制的直接转矩控制策略，有效减小了直接转矩控制方法的转矩脉动，并保持了功率器件恒定的开关频率。实验结果表明EKF准确地观测了电机转速和磁链，所构建的无速度传感器DTC控制系统具有良好的转速和转矩控制性能。

... 卡尔曼滤波算法^[5,6,7]是目前常见的无传感器控制方法,它的实质是对系统的状态向量进行重构,它以#cod#x0201c ...

2012

0.0

. 2012, 29(7):921-927

Speed estimation for permanent magnet synchronous motor based on robust extended Kalman filter

基于抗差扩展卡尔曼滤波器的永磁同步电机转速估计策略

Yin Zhong-gang , Zhang Rui-feng , Zhong Yan-ru

尹忠刚, 张瑞峰, 钟彦儒

通过分析粗差对扩展卡尔曼滤波器(extended Kalman filte,EKF)状态估计的影响,对无速度传感器矢量控制的永磁同步电机的转速,提出了一种基于抗差扩展卡尔曼滤波器(robust extended Kalman filter,REKF)的估计方法.建立了永磁同步电机的REKF模型,探讨了永磁同步电机在粗差干扰下引入REKF能否获得优于EKF的估计性能这一问题,比较了REKF与EKF在遇到外部粗差干扰或内部估算粗差干扰时转速和磁链的变化.仿真和实验结果表明REKF较EKF而言具有更好的抗粗差性能, 使系统遇到干扰时能更快收敛.

... 卡尔曼滤波算法^[5,6,7]是目前常见的无传感器控制方法,它的实质是对系统的状态向量进行重构,它以#cod#x0201c ...

2008

0.0

. 2008, 28(33):75-81 DOI:doi:10.3321/j.issn:0258-8013.2008.33.013

Direct torque control of permanent magnet synchronous motors based on extended Kalman filter observer of flux linkage

采用扩展卡尔曼滤波磁链观测器的永磁同步电机直接转矩控制

Chen Zhen , Liu Xiang-dong , Jin Yong-qiang

陈振, 刘向东, 靳永强

This paper proposed that extended Kalman filter(EKF) observer was applied to the direct torque control (DTC) of permanent magnet synchronous motor(PMSM). The EKF observed the stator voltage and current to estimate rotor speed, rotor position, stator flux linkage and torque. Based on the estimation, the sensorless speed control system of PMSM was built. Simultaneously, by improving conventional EKF estimated equation of state, this method raised the accuracy of velocity estimation. The EKF observer provides a good optimal state estimation of PMSM which is a system of nonlinear, parameter variations and disturbance. Stability properties of PMSM control system based on EKF was proved. The simulation results show that this method can estimate the state variables accurately, improve the performance of the direct torque control of PMSM.

提出利用卡尔曼滤波(extended Kalman filter，EKF)观测器对永磁同步电机(permanent magnet synchronous motor，PMSM)直接转矩控制(direct torque control，DTC)系统进行精确参数估计的方法。通过检测定子电压和电流，应用EKF观测器精确估计电机的定子磁链、电机转速和转子位置，间接估计转矩，近而实现PMSM的无速度传感器控制；同时改进常规的EKF估计状态方程，提高速度估计的精确性，并证明了基于EKF的控制系统的稳定性定理。仿真结果表明该方法减小了系统的非线性、参数变化以及干扰带来的影响，EKF能够准确估计状态变量，提高了直接转矩控制的性能。

... 卡尔曼滤波算法^[5,6,7]是目前常见的无传感器控制方法,它的实质是对系统的状态向量进行重构,它以#cod#x0201c ...

2009

0.0

... 在实际控制中,转子磁链和定子电感等参数的摄动都对转子速度和角度观测值的准确性有较大的影响,造成转子参数的观测存在一定误差,为此国外有学者将这些电机参数作为方程变量加入到卡尔曼滤波器中进行辨识^[8,9],以此来提高观测的准确性 ...

2010

0.0

1999

0.0

... 为解决这类问题,Hsieh等^[10]提出一种应用于线性系统上的最优两段卡尔曼滤波器(Optimal two-stage Kalman estimator,OTSKE),该滤波器在本质上是对卡尔曼滤波器(Kalman filter,KF)进行了算法优化,通过坐标变换的方法将卡尔曼滤波器的计算过程进行了分解,降低了运算矩阵的阶数,可以在一定程度上减轻卡尔曼滤波器的计算负担 ...

2001

0.0

... 进一步深入的研究^{[11,12,13,14]}将这种算法推广使用到非线性系统上,可以适用于更为普遍的实际情况中 ...

2000

0.0

... 进一步深入的研究^{[11,12,13,14]}将这种算法推广使用到非线性系统上,可以适用于更为普遍的实际情况中 ...

... 通过进行矩阵变换,并将其代入到扩展卡尔曼滤波方程(5)~(9)中,根据一一对应关系^[12],就可以得到NTSEKF算法的第一阶段状态参数预测方程组如下: ...

2006

0.0

... 进一步深入的研究^{[11,12,13,14]}将这种算法推广使用到非线性系统上,可以适用于更为普遍的实际情况中 ...

2009

0.0

... 进一步深入的研究^{[11,12,13,14]}将这种算法推广使用到非线性系统上,可以适用于更为普遍的实际情况中 ...

... 1 离散化电机模型的建立假设磁路不饱和,空间磁场呈正弦分布,不计磁滞和涡流损耗影响,永磁同步电机在两相旋转dq坐标系下的离散状态方程如下^[14]: ...