基于模型诊断是用人工智能方法对系统进行监控的一种方法, 使用设备的内部结构与行为的知识进行诊断工作, 其设备依赖性低, 且不依赖专家知识, 因此成为人工智能的一个主要理论研究及应用方向^{[1, 2, 3]}。最初, 基于模型诊断方法是一种静态方法, 判断系统中部件故障存在与否^[4]; 而近年来出现的离散事件系统基于模型诊断是一种动态的诊断方法, 通过判断观测与模型的相容路径来得到系统故障及原因, 因其诊断过程中不需要系统停机, 因此逐渐受到更多领域专家的重视^{[5, 6]}。在离散事件系统基于模型诊断中, 出现了诊断器^{[6, 7]}、同步^[8]等经典理论方法及通讯网络诊断^[9]、程序正确性验证^[10]等应用。

随着系统的复杂性不断增加, 模型的规模也随之增加, 这导致诊断需要面对庞大的计算量, 因此, 出现了降低模型规模, 从而降低计算量的分布式方法^{[11, 12]}。在分布式方法中, 全局模型被划分为多个相互通讯的子模型, 每个子模型独立计算诊断。因其计算效率较高, 一些经典的全局诊断方法被过渡到分布式中; 而基于分布式的诊断方法也被提出和改进。以求降低复杂度, 得到更好的计算效率。

诊断问题有一个前提条件, 那就是待诊断系统必须是可诊断的。为了精确地诊断故障, 在系统运行前, 诊断系统需要判定可诊断性。对系统的可诊断性研究主要针对两个主要问题:不同模型条件下的可诊断性判定; 可诊断性判定方法效率的改进。

不同模型条件下的可诊断性主要针对的是不同离散事件系统下的可诊断性问题, 这一类问题在基本的可诊断性判定下考虑到模型本身的特性, 在一定的约束条件下进行判定:文献[13]提出了随机离散事件系统中的可诊断性判定方法, 随机离散事件系统的事件依赖概率分布出现, 同时依赖概率转移到不确定的状态中, 系统的可诊断性被定义为依赖某种分布, 在一定程度上能够保证故障被诊断出来; 文献[14]提出了在模糊离散事件系统下的可诊断性判定方法, 在模糊离散事件系统中, 事件被赋予隶属度, 可诊断性表示为满足一定隶属度的故障在某种程度上被区分。

可诊断性判定方法效率的改进主要针对可诊断性本身, 这一类问题仅考虑判定算法的改进、模型的编译或分解。文献[6]提出的诊断器方法, 通过编译模型判定可诊断性; 文献[8]提出了双树方法, 通过同步判定可诊断性; 而之后的可诊断性方法通常是对上述两种方法的改进。

分布式系统上的可诊断性是上述两类问题的共同关注点, 分布式系统既是一种特定的模型结构, 同时, 由于分布式系统的规模较小, 相当于降低了空间复杂度, 因此也提高了可诊断性的判定效率。

在分布式系统上的可诊断性通常效率较高, 但是由于观测长度的不足或局部传感器分布的不恰当等原因, 分布式系统的可诊断性与全局系统的可诊断性未必一致, 此时产生了同步操作:向邻居寻求帮助信息, 这种同步通常是随机的, 并没有考虑是否能够解决本地的可诊断性。而且, 同步操作本身较为消耗时间, 因此产生了两个问题:①是否能够得到某种方法, 在保证能够计算可诊断性的前提下, 尽量少地执行同步操作; ②是否能够得出某种选择策略, 在保证能够计算可诊断性的前提下, 使得通讯及本地计算成本最小。

在考虑局部可诊断性之后, 根据不同的观测序列将不可诊断的语言在局部进行分组, 并将子系统之间的信息传递分为三个递进的等级, 尽量少地采用同步操作, 而从全局角度, 将三个递进等级的操作定义为启发式值, 根据不同的策略, 结合不同的权值, 得到符合策略要求的分布式可诊断性解决过程, 在解决可诊断性的全局角度上, 定量评价一个分布式系统的可诊断性; 显然, 若能够通过较少的同步或信息交互即能得到可诊断性结果, 那么该分布式系统的可诊断性较好。

我们用自动机来描述离散事件系统的行为, 一个分布式系统被定义为一组自动机:

定义1(分布式系统)^[9]:一个分布式系统是一组子系统, 每个子系统被定义为一个五元组自动机:G_i=(Q_i, E_i, T_i, I_i, F_i)。

其中Q_i是子系统的状态集合, E_i是子系统的事件集合, T_i是子系统的转移函数集合, T_i⊆Q_i× E_i× Q_i, I_i和F_i分别是子系统的初始状态集合和终止状态集合, I_i⊆Q_i, F_i⊆Q_i。事件集合E_i中包含四个彼此独立的子集。是四类不同的事件:故障事件集合 Eif, 正常事件集合 Ein, 可观测事件集合 Eio以及通讯事件集合 Eic, 四个集合彼此独立。并且, 除通讯事件外, 任意事件都是子系统内部事件。即:∀ E_i, E_j, E_i∩ E_j⊆ Eic∪ Ejc, i≠ j。

在一个子系统中全部事件序列组合被记为E^* , 在E^* 上能够被子系统所接受的组合被定义为语言l, 描述子系统内部的行为。子系统上的语言集合记为L(G_i), L(G_i⊆)E^* 。L(G_i)表示的是在子系统G_i上全部可能的行为轨迹。在子系统中, 仅有可观测事件集合是能够被外界探测到, 用于推理系统实际行为的, 因此, 在诊断过程及可诊断性判定过程中, 语言中的部分事件被“ 抹去” , 根据不同的需要, 事件集合被投影到相应的子集中, 定义可观测的映射函数如下:

Po(e)=e, ife∈Eioε, ife∈Ei\Eio

而在语言上, 也存在着由语言到可观测语言的投影:P(ε )=ε , P_o(le)=P_o(l)P_o(e)。相应地, 事件集合和语言集合也可以投影到故障事件集合和通讯事件集合上, 以求得相应的结果。

这类投影存在着逆投影: Po-1(l)={l'|l'∈ L(G_i), P_o(l')=l}。逆投影得到的是一个语言集合。根据逆投影的结果, 可以得到具有相同观测序列的语言集合 Po-1(l), 在集合 Po-1(l)中向故障事件集合做投影, 得到语言中所包含的故障, 若该集合上向故障事件集合投影得到相同的结果, 则当前的语言集合是可诊断的, 否则, 是不可诊断的。对语言集合中的全部语言进行类似的操作, 可以得到子系统的可诊断性结果; 对每一个子系统进行可诊断性判定, 得到整个分布式系统的可诊断性。

定义2(局部可诊断)^[9]:若∀ l∈ L(G_i), ∀ |P_o(l)|> n, ∀ l'∈ Po-1(P_o(l)), P_f(l)=P_f(l'), n∈ N, 则子系统G_i是局部可诊断的, 否则, 子系统G_i是局部不可诊断的。

实际上, 局部可诊断性判定的是在子系统中具有完全相同可观测投影的语言的故障是否相同。如果故障不同而观测相同, 表明具有相同表征的系统行为隐含着不同的故障, 不能够被正确地检测出来, 对系统的安全性造成威胁。可诊断性判定的主要任务就是找出这类问题, 并通过各种方法解决。在分布式系统中, 可以通过与其他部件交换信息来确定部分不确定语言的发生, 这些不确定的语言被定义为一个局部组:

定义3(局部组):一个局部组被定义为一个语言集合, 用Group(l, G_i)表示。Group(l, G_i)={l|l∈ L(G_i)∩ Po-1(P_o(l)), ∃l'∈ Po-1(P_o(l)), P_f(l)≠ P_f(l')}

局部组中的语言是局部不可诊断的语言。当局部存在不可诊断的语言时, 通过同步方法来进行扩展, 得到扩展的观测信息及时序信息, 用于区分局部的可诊断性。用同步来进行观测信息的扩展, 用有向无环图来表示事件之间的时序关系。

定义4(同步):同步操作是两个自动机之间的操作:

Trim(G₁⊗G₂)=(Q₁× Q₂, E₁∪ E₂, T', I₁× I₂, F₁× F₂)其中T'被定义如下:

T'={((q₁× q₂), e, (q'₁× q'₂))|∃e₁, e₂, ((q₁, e₁, q'₁)∈ T₁)∧ ((q₂, e₂, q'₂)∈ T₂)∧ (e₁∩ (E₁∩ E₂)=e₂∩ (E₁∩ E₂)), e=e₁∩ e₂}

定义5(有向无环图)^[15]:一个有向无环图定义为一个二元组:D=(N, A)。

其中N是节点集合, 表示自动机G中的一个可观测事件; A是有向边集合, 表示可观测事件之间的时序关系。若在一个语言中, 两个可观测事件直接相邻, 则在有向无环图中存在一条边, 由前一个事件指向后一个事件, 称为直接可达, 记为n_i→ n_i+1; 而若两个可观测事件之间具有时序关系, 但是不直接相邻, 则在有向无环图中存在一条路径, 由时序在前的事件到达时序在后的事件, 称为间接可达, 记为n_i→ n_j。并且, 存在如下性质:若n_i→ n_j, 则如下路径存在:n_i→ n_i+1…→ n_j。

同样地, 若两个节点存在直接可达或者间接可达关系, 则二者存在时序关系:∃n_i→ n_j⇒ n_i≺n_j, ., 即n_i在n_j前。

当局部不可诊断时, 提出一种分层结构来进行扩展, 判定可诊断性, 根据约束模型的范围, 可诊断性被分为三层:语言的可诊断性、子系统的可诊断性以及分布式系统的可诊断性。对于子系统, 当且仅当子系统的全部语言是可诊断的, 子系统是可诊断的; 对于分布式系统, 当且仅当任意一个子系统是可诊断或通过通讯可诊断, 分布式系统是可诊断的。

在语言的可诊断性判定中, 定义语言的可诊断性标签d_ij, 表示在第i个子系统中的第j个语言。若该语言可诊断, 则d_ij=1; 否则d_ij=0。子系统的可诊断性依赖于语言的可诊断性, 定义标签为d_i, 当子系统中的全部语言可诊断时, d_i=1; 否则子系统不可诊断, d_i=0。分布式系统的可诊断性标签标记为d, d为一个二元向量dx, dy。

dx= ∏i=1nd_i, 当dx=0时, 分布式系统不可诊断, dx=1时, 分布式系统是局部可诊断的。dy= ∏i=1nk_i, 其中:

k_i= 2i, ifsyn-diagnosable(i)0, else

其中syn-diagnosable(i)表示的是通过通讯可诊断:即在有限次的同步之后, 子系统可诊断。dy的值可以判断分布式系统中有多少子系统是通过同步才可以诊断, 并且能够逐一地标定它们。

在这三层的判定可诊断性的结构中, 我们自底向上逐步判定每一层的可诊断性, 在语言层, 我们用局部的投影函数得到结果, 标记语言可诊断性, 并按照定义3分组; 在子系统层, 用语言可诊断性标签求得可诊断性, 并得到子系统上的时间因果图; 在分布式系统中, 先用子系统的可诊断性标签求得可诊断性, 然后执行分布式系统之间的同步, 判定同步的可诊断性, 求得全局的通讯可诊断性。

在子系统不可诊断时, 同步与之共享通讯事件的子系统, 可以改变当前子系统的可诊断性。其原因是通过同步, 子系统扩展了观测, 从而得到更多的信息来判断可诊断性, 同步的过程在可诊断性的角度上看, 是一个扩展观测、从而推出局部路径的过程。但是, 仅从可诊断性角度考虑, 同步过程是可以化简的。我们提出一个递进的过程, 通过更简单的操作扩展观测, 判定可诊断性。这个扩展观测的操作可以分为三个阶段, 复杂度是逐步递进的。如果前一个阶段的操作能够判定可诊断性, 后面的操作将不被执行。因此部分降低了同步过程的复杂度。

分别给出这三个阶段及判定条件:连接; 排序; 同步。

(1)连接:实质上, 连接是通过通讯不同的邻居, 在具有局部相同观测的语言上添加不同的观测来判定可诊断性, 如果存在如下条件:∀ l, l'∈ Group(l, G_i), P_c(l)≠ P_c(l'), 则可以用连接操作来进行可诊断性判定。

若组中每一个语言具有不同的通讯事件, 这表示每一个语言通讯到不同的子系统, 由于子系统之间的可观测事件交集为空, 那么通讯过程实际上扩展了可观测事件序列。若当前组中全部语言均能够通过通讯事件扩展, 从而被区分, 那么系统是通讯可诊断的。

设C(l)是与l通讯的全部语言的集合, 若在组中, 存在语言使得l_m∈ ∈ Group(l, G_i), l_n∈ ∈ Group(l, G_i)l_m, P_o(C(l_m))≠ P_o(C(l_n))则l_i, l_j是通讯可诊断的。简单地说, 若能存在一个语言, 能够通过通讯扩展, 使得该语言区别于其他的组成员, 则该语言是通讯可诊断的。

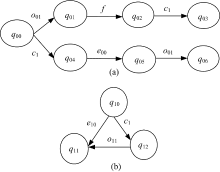
连接操作可以判断子系统的通讯可诊断性是因为通讯事件与观测事件之间的时序关系, 以及通讯事件本身的性质所决定的。通讯事件虽然是不可观测的, 但是在子系统之间, 通讯事件的发生是同时的, 因此, 一个通讯事件的发生可以判定时序小于该通讯事件的事件的发生, 两个子系统的观测可以通过时序的推理得到扩展, 从而得到可诊断性。如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 连接例Fig.1 An example of link

(a)中两个语言是不可诊断的, 但是由于通讯事件c₁的存在, 通讯到(b)的自动机, 若o₁₁发生, 则可以推断c₁已经发生, 并且在(a)中同时发生了c₁, 因此可以推断f发生。

(2)排序:若具有相同观测的语言通讯到同一个子系统, 此时邻居的观测不能直接推理出是哪一个语言, 但是通讯事件与观测事件之间的时序不同, 也可以作为区分可诊断性的依据, 其条件是∃l_m, l_n∈ Group(l, G_i), P_c(l_m)=P_c(l_n), C(l_m)∩ C(l_n)≠ ⌀。当存在语言满足上述关系时, 在有向无环图中判断观测与通讯事件的时序关系, 若能满足以下条件:∃l, l'∈ Group(l, G_i), ∃c∈ E_i∩ E_j, ∃e∈ P_o(l∩ l')使得c≺e, e⊂l, e≺c, e⊂l'。并且∃e'∈ Ejo, c≺e'。

在不可诊断语言的组中, 相同的通讯事件将得到相同的可观测事件扩展, 但是由于时序关系不同, 扩展的观测在不可诊断语言中的位置不同, 从而得到不同的扩展可观测序列, 最终得到通讯可诊断语言, 如图2所示。

图2与图1中所示的结构相同, 但是通讯事件不同。由于通讯事件c₁在图2(a)中与可观测事件o₀₁的时序在不同的语言中是不同的, 通讯之前若得到可观测事件o₀₁, 则可以判断故障f发生, 若在通讯之后得到可观测事件o₀₁, 则故障f没有发生。

(3)同步:当上述线性的执行过程不能判断可诊断性, 根据定义4的操作, 同步共享同一个通讯事件的自动机, 得到两个子系统的剪枝同步自动机, 在剪枝自动机上, 重新判定可诊断性。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 排序例Fig.2 An example of ordering

上述的三个递进的过程是在子系统内部的组中进行, 如果存在一组的语言全部被判定为可诊断, 或者k-1个语言是可诊断的, k是组中语言的个数。则这一组语言将被全部标为可诊断。当子系统中的全部语言被标记为可诊断, 则该子系统被标为可诊断。接下来一节我们将讨论在分布式系统角度下考虑的可诊断性判定过程以及通过可诊断性标签的值及其改变对子系统可诊断性作出的定位。

在语言层和子系统层上, 通过连接、排序、同步三种递进的方法可以得到子系统的局部可诊断性以及通讯可诊断性。而在全局角度, 同步的选择策略对于通讯可诊断性的判定效率有着一定的影响。较好的同步选择策略可以在正确地判断可诊断性的同时, 尽量少地与邻居通讯或同步; 或者, 在通讯成本和同步计算成本不相等时, 尽量减少判定可诊断性的成本。

当不考虑解决局部的可诊断性及通讯过程时, 我们可以将全局的可诊断性认为是这样一个问题:一个带有平行边的图, 是否每一个点都能够根据若干条边, 满足一个确定的特性。而进一步地, 在保持这种特性的前提下, 是否能够取消某些边, 使得图的解决成本更低?形式化这个问题, 并给出基本算法, 从全局角度来判断整个系统的可诊断性。在基本算法的基础上, 进一步讨论优化成本问题。

在全局角度通讯可诊断性的判定过程通常按如下步骤:①判断局部可诊断性; ②在局部可诊断性的结果上进行分组, 生成有向无环图表示时序, 并进行标记; ③选择一个局部不可诊断的子系统; ④递进地判断通讯可诊断性, 直到当前子系统是通讯可诊断的, 或者同步到全局为止; ⑤重复③、④过程, 直到每一个子系统都是局部可诊断或通讯可诊断的。

需要注意的是, 在第4个步骤中, 若当前子系统的同步结果与全部分布式系统的同步结果相等时, 该子系统仍是通讯不可诊断的, 则该子系统必然不可诊断, 从而, 整个分布式系统也不可诊断。此时无需再重复执行3, 4两个步骤, 而返回通讯不可诊断的结果。算法1描述的是在全局角度判断通讯可诊断性的过程。

算法1 判断通讯可诊断性

输入:分布式系统:G_i=(Q_i, E_i, T_i, I_i, F_i)

输出:通讯可诊断性结果dy, 局部可诊断性结果dx

初始化:局部可诊断性标签∀ d_ij=0, List=ε

(1)LocalDia(G_i) //计算全部子系统的局部可诊断性

(2)Mark(d_ij) //标记全部语言的可诊断性

(3)d_i= ∏j=0nd_ij //标记子系统的可诊断性

(4)∀ i, d_i=0, ∀ l_ij, d_ij=0, Group(l_ij, G_i) //对所有局部不可诊断的语言分组

(5)∀ i, d_i=0, Get(G_i, D_i) //生成局部不可诊断子系统的有向无环图

(6)L=List(G_i) //按照一定的规则对子系统进行排序

(7)While(L)≠ ε

(8) j=TestS D(First(L)) //选择一个子系统测试通讯可诊断性, 返回同步数

(9) if j=n

(10) dx=0

(11)else

(12) Delete(First(L))

(13)EndWhile

(14)EndWhile

(15) dy= ∑i∈dm=0nk_i

在算法1中可知, 最坏情况下, 将全部子系统同步, 得到的同步积结果依旧不可诊断时, 分布式系统是不可诊断的。而通常情况下, 一个分布式系统会得到一个通讯可诊断的结果。如果满足观测的公平性, 分布式系统与其同步后的结果在可诊断性上是等价的, 该性质也可保证通讯可诊断性的结果与同步后的全局可诊断性是等价的。

算法1给出的是最基本的通讯可诊断性判定过程, 并不考虑通讯成本及计算的成本。进一步地, 考虑各种成本, 对通讯可诊断性的判定过程进行优化。

通讯可诊断性判定的成本主要包括局部可诊断性判定、通讯成本以及通讯后的可诊断性判定。由于局部可诊断性判定的结果是确定的, 这部分成本不计入优化考虑。通讯成本指的是子系统G_i与子系统G_j通讯, 发出通讯事件的成本; 若子系统G_i与子系统G_j是通过多个子系统通讯, 则通讯成本包括全部相关的通讯事件成本。通讯后的可诊断性判定成本包括判定当前子系统情况, 并通过连接、排序或同步等过程, 最终判定通讯可诊断性的计算成本。

这种方法可以被概括成一个在全局角度下的加权图的问题:存在一个无向、带有平行边的加权图, 每一个点都需要通过某些边满足自身的性质, 满足性质的同时, 也带来了本地的计算成本以及边的通讯成本, 如何求得一个子图, 使得满足每一个点的性质的同时, 使得全局的成本最小。

每个子系统被视作加权图中的一个节点, 局部可诊断性及通讯可诊断性被定义为点的性质。共享同一个通讯事件的子系统之间存在一条边, 并且每存在一个通讯事件, 建立一条边。通讯事件的通讯成本作为该边的权。

全局的通讯判定局部可诊断性的成本为C(G_i); 若G_i不可诊断, 分组及建立有向无环图的成本为C(N_i); 在G_i中存在k个通讯事件, 每个通讯事件的成本为C(c_ik); 通讯可诊断性计算过程中, 连接、排序及同步的计算成本分别为C₁, C₂, C₃。在判定通讯可诊断性时, 若当前分布式系统是通讯可诊断的, 且存在多个策略S₁, S₂, …, S_m, 使得该分布式系统通讯可诊断, 则全局成本为min( ∑i=1nC(G_i)+C(N_i)+C(S_k)), 其中S_k等于在策略下的计算成本。对于一个确定的分布式系统C(G_i)+C(N_i)是固定的, 全局成本的最小值实际上是求minC(S_k)。算法2给出的是求解一个通讯可诊断性计算策略的方法。

算法2:通讯策略的求解

输入:分布式系统G_i=(Q_i, E_i, T_i, I_i, F_i), 通讯事件成本C(c_ik), 计算成本C₁, C₂, C₃

输出:策略S_k={(c_1i, c_1j), (c_2m, c_2n), …}, 策略成本C(S_k)

初始化:S_k=⌀, C(S_k)=0, ∀ i, s'_i=0, s″_i=0

(1)While∀ G_i∈ L, s_i≠ 0

(2) L=List(G_i) // 对分布式系统进行排序

(3) i=First(L) // 选择一个子系统

(4) if d_i=0 // 如果当前子系统局部不可诊断

(5) ComLD(G_i) // 选择当前子系统的通讯策略

(6) s'_i=a₁× C₁+a₂× C₂+a₃× C₃

//当前计算成本为连接、排序、同步成本之和, //其中a₁, a₂, a₃分别为选择相应策略进行判定的//语言数, 且a₁, a₂, a₃之和为一组中语言的个数。

(7) s″_i=∑ C(c_ik) //计算通讯成本

(8) s_i=s'_i+s″_i, Reserve(c_ik) //保留当前策略

(9) Mark=Mark(G_k, c_ik) //标记全部已经建立通讯的子系统

(10) ∀ G_m∈ Mark, s″_m=s″_m-c_ik //在已经建立通讯的子系统中将通讯成本减去

(11) L=ReList(L) //重新列表

(12)EndWhile

(13)C(S_k)= ∑i=1ns_i //计算全部成本

考虑到每一个局部可诊断的最优未必在全局上最优, 其中通讯的成本以及可重用的通讯事件对全局的结果有影响, 因此这种策略的选择变成了一个搜索过程。从具有最低成本的子系统开始, 得到一个局部的通讯策略, 选择部分通讯事件计算通讯可诊断性, 并尽量重复利用通讯事件, 使得通讯成本较小。而在列表过程中, 列表策略的不同, 也会导致成本存在不同。策略的选择可以作为一个带有启发式的搜索过程。

可诊断性是诊断系统的一种性质。通常对于一个系统, 我们只定性地判断可诊断与不可诊断, 而在分布式的诊断系统中, 每一个子系统的可诊断性被独立地定性, 分布式系统通过全部子系统来定性。而不能独立定义可诊断性的分布式系统, 其可诊断性显然弱于独立的局部可诊断。如果需要定量地描述分布式系统的可诊断性, 则用一些参数来评价可诊断性。

对于一个分布式系统, 其任意子系统是局部可诊断的, 则该分布式系统是可诊断的。若该分布式系统中, 部分子系统局部可诊断, 而部分子系统是通讯可诊断的。则存在两个参数可以对其进行描述, 一是局部可诊断子系统所占比例, 二是同步操作次数的分布。

局部可诊断子系统所占比例可以简单地定义为i/n, 其中i是局部可诊断的子系统数量, n是分布式系统中子系统的数量。这个参数分布在[0, 1]上, 当全部子系统局部不可诊断时, 达到最小值0, 全部子系统局部可诊断时, 达到最大值1。

同步操作次数的分布可以定义为一个n元数组m=[i₁, i₂, …, i_n], 其中i_j的值是使第j个子系统通讯可诊断, 需要一次性同步的子系统数, 分布在[0, +∞ ]上。这里一次性同步是指将多个自动机逐一同步:Trim(G₁⊗G₂⊗…⊗G_i); 而不是与一组自动机中的自动机同步多次:Trim(G₁⊗G₂), Trim(G₁⊗G₃), …, Trim(G₁⊗G_i)。当i_j=0时, 该子系统是局部可诊断的; 当i_j在+∞ 上时, 该子系统是通讯不可诊断的; 特别地, (∃i_k=n)∧ (∀ i_j≤ n)时, 该系统是全局可诊断的。而通常情况下, 当m的平均值较小时, 系统的计算和通讯成本较小; 而当m的平均值较大时, 则表示每个子系统需要同步多个子系统才能判定通讯可诊断性, 此时计算和通讯的成本较高。在一个分布式系统中, 若m的方差较小, 表示该分布式系统的通讯较多, 且分解较为均匀; 若m的方差较大, 则该分布式系统的分解存在一定的问题, 具有较高值的部分子系统的划分可能存在着问题, 可以进一步添加观测或重新分解该部分子系统, 从而使该部分具有较为良好的通讯可诊断性。

用一个实例来描述通讯可诊断性判定的过程及评价。图3是一个分布式自动机组。不同的语言具有相同的观测, 并且具有不同的通讯事件。在图3(a)中, 自动机中的l₁, l₂, l₄具有相同的可观测投影, 但是l₄存在扩展的观测obs₂, 因此与l₁, l₂不同。设l₁, l₂具有不同的故障事件, 因此l₁, l₂是不可诊断的。被分为一个组。在图3(b)中的通讯事件c₁可以与l₁通讯, 在l₁上扩展观测obs₃; 在图3(c)中的通讯事件c₂可以与l₂通讯, 在l₂上扩展观测obs₄; 那么, 无论选择扩展l₁或者l₂, 都可以得到一个与之前不同的可观测投影, 因此该系统是通讯可诊断的。

设c₁的通讯成本为cost(c₁), c₂的通讯成本为cost(c₂), 通讯c₁在图3(a)中的计算成本为cost(l₁), 通讯c₂在图3(a)中的计算成本为cost(c₂), 比较cost(c₁)+cost(l₁)与cost(c₂)+cost(l₂), 成本较低的作为判断通讯可诊断性的选择策略。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 选择策略举例Fig.3 An example of strategy in choosing

这种选择策略不仅在判定通讯可诊断性的过程中可以被应用, 诊断过程中, 当本地的系统故障不能被诊断, 需要通讯来辅助诊断本地故障时, 也可以采用离线通讯可诊断判定的通讯策略来有效地判定本地故障。

用实验验证i/n对通讯可诊断性判定效率的影响, 同时讨论子系统模型规模、分布式系统规模对通讯可诊断性判定的影响。实验建立在不同子系统规模的分布式系统上, 且子系统的规模不同, 测试用算法1判定通讯可诊断性测试的效率。实验结果见表1。

可以看出, 当局部可诊断的比例较高时, 判定效率较高, 反之则较低。这是因为在判定通讯可诊断性过程中, 向其他子系统通讯, 计算同步, 消耗较多时间。并且, 选择被同步子系统的策略对判定通讯可诊断性的效率也存在着影响。

通讯可诊断性判定的效率随着分布式系统规模增长而降低是因为:测试通讯可诊断性时, 当前子系统可能存在多个可以通讯的候选子系统, 部分时间消耗在对候选子系统的选择上。

表1

Table 1

表1(Table 1)

表1 实验结果 Table 1 Experimental results ms 局部可诊 断比例/% 子系统× 状态数 10× 10 10× 20 20× 10 20× 20 40× 10 40× 20 100× 10 100× 20 100× 100 95 62 108 391 578 2688 6328 5641 10219 46060 90 63 266 453 1782 2906 7203 7828 11281 47109 80 78 375 547 2296 3328 9047 9156 13610 49531 70 109 548 718 3110 4063 12750 13875 18297 54219 60 172 828 1000 4469 5234 18828 25974 30025 67875 50 297 1344 1454 6781 7265 28906 42506 67030 110297

表1 实验结果 Table 1 Experimental results ms

同时, 分布式系统规模增加, 需要判定通讯可诊断性的子系统也随之增加, 因此导致通讯可诊断性判定的效率降低。

提出了在分布式系统的可诊断性判定过程中的简化算法, 通过对子系统的化简及时序的添加, 化简同步过程, 提高测试通讯可诊断性的效率。提出了在通讯可诊断性判定过程中的成本问题及其解决该问题的算法。

进一步地, 改进了同步过程中对可通讯候选子系统的选择策略, 提高了通讯可诊断性的判定效率。同时, 讨论了在分布式系统的通讯可诊断性中, 是否存在同步的上限, 使得任意子系统在通讯可诊断性判定过程中, 同步不超过该上限的子系统即可得到通讯可诊断的结果。