引用本文
刘磊, 王燕燕, 申春, 李玉祥, 刘雷. Bellman-Ford算法性能可移植的GPU并行优化. 2015, 45(5): 1559-1564
LIU Lei, WANG Yan-yan, SHEN Chun, LI Yu-xiang, LIU Lei. Performance portable GPU parallel optimization technique on Bellman-Ford algorithm. Journal of Jilin University Engineering and Technology Edition, 2015, 45(5): 1559-1564  
Permissions
Copyright©2015, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
Bellman-Ford算法性能可移植的GPU并行优化
刘磊1, 王燕燕1, 申春1, 李玉祥2, 刘雷3
1.吉林大学 计算机科学与技术学院,长春 130012
2.中信证券有限公司,北京 100026
3.中国科学院 计算技术研究所,北京 100190
申春(1971-),女,讲师,博士.研究方向:软件理论与技术.E-mail:shenchun@jlu.edu.cn

作者简介:刘磊(1960-),男,教授,博士生导师.研究方向:软件理论与技术.E-mail:liulei@jlu.edu.cn

基金:吉林省重大科技攻关项目(20130206052GX); “863”国家高技术研究发展计划项目(2012AA010902); “973”国家重点基础研究计划项目(2011CB302500)
摘要

提出了一种面向GPU的性能可移植的并行归约求极值优化算法和全局访存优化算法,对Bellman-Ford算法进行并行化改造,以解决不同类型GPU设备上都存在的并行粒度不足和全局内存访问不连续等问题。实验结果表明:本文的优化算法在NVIDIA和AMD的多款GPU设备上都取得了很好的效果,经本文算法优化后的程序性能较原始GPU并行版本提升3~6倍。

关键词: 计算机软件; Bellman-Ford算法; GPU并行编程及优化技术; 并行归约算法; 性能可移植性
中图分类号:TP302 文献标志码:A 文章编号:1671-5497(2015)05-1559-06
Performance portable GPU parallel optimization technique on Bellman-Ford algorithm
LIU Lei1, WANG Yan-yan1, SHEN Chun1, LI Yu-xiang2, LIU Lei3
1.College of Computer Science and Technology, Jilin University, Changchun 130012, China
2.Citic Securities Co., Ltd., Beijing 100026, China
3.Institute of Computing Technology, Chinese Academy of Sciences, Beijing 100190, China
Abstract

A GPU-oriented performance portable parallel reduction algorithm for extreme value optimization and a global memory access optimization algorithm are presented to resolve the issues of deficient parallel granularity and global memory access conflict on different GPUs. Experimental results show that the presented optimization algorithms can obtain high performance on a variety of NVIDIA and AMD GPU devices, gaining a speedup of 3 to 6 times than existing methods.

Keyword: computer software; Bellman-Ford algorithm; GPU parallel programing and optimization techniques; parallel reduction algorithm; performance portability
0 引 言

Bellman-Ford算法是一种常见的求解单源最短路径问题的算法, 在计算机网络、智能交通等诸多领域[1, 2, 3]中有着广泛的应用, 但是由于该算法时间复杂度很高, 在多核处理器上的并行性能很难满足业界需求。GPU因其吞吐量高、速度快、显存带宽高等优点逐渐成为提高计算性能的主要途径[4, 5], 采用GPU并行化, 可以取得更好的性能。但是, GPU并行编程尤其是性能优化非常困难, 现有的GPU上的Bellman-Ford算法的并行粒度较低, 而且也很难在不同的GPU设备上保证算法的性能可移植性。

本文提出了一种面向GPU性能可移植的并行规约求极值优化算法和全局访存优化算法对Bellman-Ford算法进行并行化改造, 以解决不同类型GPU设备上都存在的并行粒度不足和全局内存访问不连续等问题。通过在NVIDIA GeForce GTX 690、NVIDIA GeForce GTX TITAN、AMD Pitcairn等多款GPU设备上对本文提出的优化算法进行实验, 在多款GPU设备上都取得了很好的性能提升, 比CPU串行实现性能提高约200~300倍, 比OpenMP并行版本性能提高约40~80倍, 与传统的Bellman-Ford的GPU并行实现版本相比性能提升了3~6倍。

1 Bellman-Ford算法的并行性分析
1.1 算法介绍

Bellman-For算法[6]是由查理德· 贝尔曼和莱斯特· 福特创立的, 主要用来求解单源最短路径问题。其基本思想是对所有的边不断进行松弛迭代操作, 并且同时更新每个顶点的最短路径值和其最短路径上的前驱顶点值, 达到收敛时停止迭代操作。

Bellman-Ford算法的过程可描述为:带权有向图G=(V, E), 其中V表示图顶点集合, E表示图边集合, 源点为s, 图顶点数为N=|V|, 对于图G, Bellman-Ford算法通过递推迭代方式反复对边集E中每条边进行松弛操作, 使得源点到其他每个顶点u∈ V的最短路径估计值逐渐逼近其最短距离, 总共需要迭代N-1次。每个顶点v可构造出一个最短路径长度数组序列dist1[v], dist2[v], …, distN-1[v]。对于distk[v], 其中k=1, 2, …, N-1, 可通过如下递归计算公式求出:

distk[v]=dist1[v]=edge[s][v], k=1distk[v]=min{distk-1[v], min{distk-1[j]+edge[j][v]}}, k> 11

式中:v=0, 1, …, N-1; j=0, 1, …, N-1, 为图G的顶点, 且j≠ v; dist1[v]为从源点s到终点v只经过一条边的最短路径长度; dist2[u]为从源点s最多经过两条边到达终点v的最短路径长度; distk[v]为从源点s最多经过不构成负值回路的k条边到达终点的最短路径长度。

算法的最终目的是计算出distN-1[v], 即从s到v的最短路径长度, 具体算法过程如下:

procedure Bellman-Ford(input: G, s, output:σ , η )

1 //初始化

2 for v=0 to N-1 do

3 σ 0(v)=∞ , η 0(v)=-1, σ 0(s)=0;

4 end for

5 //对所有的边进行松弛迭代操作

6 for k=1 to N-1 do

7 //对每个顶点v计算σ k(v), η k(v)

8 for v=0 to N-1 do

9 if v≠ s then

10 //计算通过其他顶点j到达顶点v的最短路径δ (v)及最短路径上前驱顶点ρ (v)

11 δ (v)=∞ , ρ (v)==-1;

12 for j=0 to N-1 do

13 if σ k-1(j)+edge[j→ v]< δ (v)and j≠ v then

14 δ (v)=σ k-1(j)+edge[j→ v];

15 ρ (v)=j;

16 end for

17 σ k(v)=MIN(σ k-1(v), δ (v));

18 if σ k(v)< σ k-1(v) then

19 η k(v)=ρ (v)

20 else

21 η k(v)=η k-1(v);

22 end for

23 end for end procedure

算法迭代N-1次收敛, σ k(v)、η k(v)指经过k次迭代后从源点s到达顶点v的最短路径值distk[v]和最短路径上的前驱顶点值; δ (v)指通过其他各顶点j到达v的路径最短值, ρ (v)指该路径上v的前驱顶点。

1.2 算法并行性分析及GPU并行实现算法

根据Bellman-Ford算法过程可知, 对每个顶点v进行初始化操作以及计算σ k(v)和η k(v)部分可以直接采用并行的方式进行处理。计算通过其他顶点j到达顶点v的最短路径δ (v)和最短路径上前驱顶点ρ (v)不能直接进行并行处理, 但是可以采用并行归约[7]方法对其进行并行处理。

设一维线程T(|V|)={t0, t1, …, t|V|-1}, 每个线程负责一个顶点, 线程tv∈ T(|V|), v=0, 1, …, |V|-1, 其线程号为v_id, 且用线程号v_id表示线程tv所处理的顶点v, 则Bellman-Ford的GPU并行算法[8]为:

procedure BF_Naive(input: G, s, output: σ , η )

1 kernel par_ Initialize_kernel(G, s, σ , η )

2 σ 0(v_id)=∞ , η 0(v_id)=-1;

3 if v_id=s then σ 0(v_id)=0;

4 end kernel

5 kernel par_bf_kernel(G, s, σ , η , k)

6 if v_id≠ s then

7 calculate δ (v_id), ρ (v_id);

8 update σ k(v_id), η k(v_id);

9 end kernel

10 prepare the OpenCL platform and input data;

11 par_Initialize_kernel(G, s, σ , η ) ; thread:T(|V|

12 for k=1 to N-1 do

13 par_bf_kernel(G, s, σ , η , k); thread:T(|V|)

14 end for end procedure

在该算法过程中, 内核函数par_Initialize_kernel负责对每个顶点v进行初始化操作, 内核函数par_bf_kernel负责对每个顶点v计算σ k(v)、η k(v), 计算时每个线程需要以串行的方式计算δ (v)、ρ (v)值, 执行|V|次循环, 线程的任务量比较重, 并行粒度不足, 算法效率低。因此, 本文采用并行归约求最小值的方法对计算通过其他顶点j到达顶点v的最短路径δ (v)和最短路径上前驱顶点ρ (v)进行并行优化处理。

2 Bellman-Ford算法的GPU并行优化
2.1 利用参数化并行归约方法实现Bellman-Ford算法的GPU并行化

从Bellman-Ford算法中可以看出, 计算顶点v的最短路径δ (v)和最短路径上前驱顶点ρ (v)的过程, 实际上是一个求最小值并计算该最短路径上v的前驱顶点ρ (v)值的过程。使用多个线程方式计算δ (v)和ρ (v)时需要保证线程间同步, 然而在GPU环境下很难在所有线程之间提供全局同步机制, 并且OpenCL中也不支持全局同步机制。为此, 本文设计并实现了一种称为参数化并行归约方式来计算δ (v)和ρ (v)。

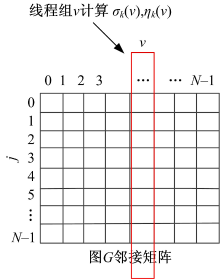
在GPU中以线程组为基本调度单位, 同一个线程组内的线程可以通过硬件支持的barrier机制来保证线程组内线程同步。通常线程组内的线程数是GPU硬件调度单位的倍数, 例如在NIVIDIA显卡中调度单位为wrap, 在AMD显卡中调度单位为wave。为了保证算法的多平台可移植性, 本文将线程组内线程数M设置为可动态调整的参数, 以M作为任务划分和归约同步的基本单位。定义二维线程(x, y)=T(M, |V|), 将线程分为|V|组, 每组有M个线程, 分别对每个顶点v计算σ k(v)、η k(v)和δ (v)、ρ (b)值进行处理, 然后用每个线程组对每个顶点b计算σ k(v)、η k(v)值, 如图1所示。每个线程组内的M个线程采用par_reduce并行归约算法计算δ (v)、ρ (v), 该算法的思路是:首先使用M个线程分别计算经过各个顶点到达顶点v的路径值, 并同时求出几条路径的最短路径值保存在δ inter(t)中, 该路径上的前驱顶点值保存在ρ inter(t)中; 以二分法的方式对中间归约结果δ inter和ρ inter继续进行归约, 该过程是一个迭代的过程, 迭代 log2M +1次结束, 且本次迭代使用的线程数是上次迭代使用线程数的一半。

图1 线程组与邻接矩阵关系图Fig.1 Relationship between thread groups and the adjacent matrix

参数化并行归约算法为par_reduce, 使用par_reduce算法对Bellman-Ford算法进行优化后的算法为BF_Reduce, 具体过程如下:

procedure BF_Reduce(input: G, s, output:σ , η )

1 par_reduce(input: M, v, G, output:δ , ρ )

2 δ inter(t)=∞ , ρ inter(t)=-1;

3 M个线程{ t| t=0, 1, …, M-1}并行执行:

4 {

5 for i=0 to N/M -1 do

6 if δ inter(t)> σ k-1(t+i* M)+edge[(t+i* M)→ v]

and (t+i* M)< |V| then

7 δ inter(t)=σ k-1(t+i* M)+edge[(t+i* M)→ v], ρ inter(t)=t+i* M;

8 end for

9 }

10 M1= M/2

11 for iter=2 to log2M +1 do

12 M1个线程{t| t=0, 1, …, M1-1}分别并行执行以下任务:

13 {

14 if δ inter(t)> δ inter(t+M1) and (t+M1)< M then

15 δ inter(t)=δ inter(t+M1), ρ inter(t)=t+M1;

16 }

17 M=M/2, M1=M1/2 ;

18 end for

19 end par_reduce

20 kernel par_bf_kernel_reduce

21 if ty≠ s then

22 par_reduce(group, ty, G); //使用参数化并行归约方法计算δ , ρ

23 Update σ k(ty)、η k(ty);

24 end kernel

25 Prepare the OpenCL platform and input data;

26 par_Initialize_kernel(G, s, σ , η ) thread:T(|V|)

27 for k=1 to N-1 do

28 par_bf_kernel_reduce(G, s, σ , η , k) thread:T(group, |V|)

29 end for end procedure

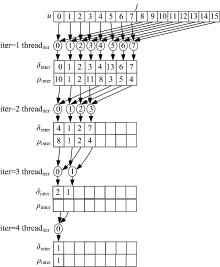
在该算法中, 根据硬件的调度单位设置组内进行归约的线程数, 使得该算法能够很好地适用于不同的GPU平台。为了简单说明par_reduce算法的过程, 图2中给出了一个当M为8(在实际计算中M是较大的数字)、顶点数N为16时par_reduce算法的归约过程。

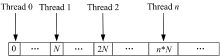
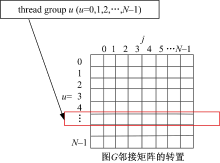
图2 并行归约求最小值的迭代过程Fig.2 Iteration process of parallel reduction for minimum value

2.2 Bellman-Ford并行算法性能可移植的优化

在par_reduce算法过程中, 每次迭代都需要频繁地访问数据, 在GPU中, 频繁访问全局内存时效率非常低, 因此采用共享内存来保存第一轮迭代结果, 然后直接对共享内存中的数据进行迭代。根据图1不难发现, 每组线程都是对图G的邻接矩阵的每一列进行归约操作, 而在计算机中矩阵的存储方式一般是按行顺序存储在内存中, 对全局内存的访问方式如图3所示, 连续地线程访问全局内存时是跳跃的, 不是连续的, 因此访存请求无法自动合并, 访存效率非常低。

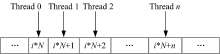
图3 对列归约时全局内存访问方式Fig.3 Global memory access mode when reducing for the col

邻接矩阵的每一列元素正好与其转置矩阵的相应行的元素对应, 一个线程组对矩阵一行元素的访问方式见图4, 访存请求可以实现自动合并, 访存效率非常高。

图4 对行归约时全局内存访问方式Fig.4 Global memory access mode when reducing for the row

为了提高全局内存的访存效率, 同时保证算法具有良好的平台适应性, 本文先对图G的邻接矩阵进行转置操作, 然后线程组对转置后邻接矩阵的每一行进行处理, 实现以合并方式访问全局内存来减少访存延时, 提高访存效率, 如图5所示。为了解决全局内存访问不连续的问题, 本文设计了BF_Reduce_Coarse优化算法, 其基本过程与BF_Reduce算法基本相同, 不同之处在于线程组每次对转置后邻接矩阵的一行元素进行并行归约。相较于算法BF_Reduce, 本文通过将BF_Naive中对δ (v)、ρ (v)的计算部分展开, 将一个线程执行的任务分配给多个线程以归约方式执行。

图5 转置后线程组和邻接矩阵关系图Fig.5 Relationship between thread groups and the adjacent matrix after matrix transposition

3 实验和分析

本文使用OpenCL[9, 10]对BF_Reduce、BF_Reduce_Coarse算法进行了编程实现, 分别在NVIDIA GeForce GTX 690、NVIDIA GeForce GTXTITAN[11, 12]、AMD Pitcairn三个GPU平台上对BF_Reduce、BF_Reduce_Coarse进行测试, 主要目的是为了说明本文提出并行优化算法具有很好的算法可移植性。

3.1 算法实验

实验时采用随机方式分别生成顶点规模为256、512、1024、2048、4096、8192的图, 并将BF_Reduce_Coarse与BF_Reduce、BF_Naive以及OpenMP进行比较分析。算法GPU执行时间的计算式为:

time(GPU)=time(kernel)+time(DataToGPU)+time(DataToCPU) (2)

3.2 实验结果与分析

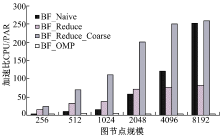
图6为BF_Reduce_Coarse、BF_Reduce、BF_Naive在NVIDIA GeForce GTX TITAN GPU平台下的性能加速比, 该平台基于NVIDIA Kepler GK110架构, 可以看出BF_Reduce_Coarse算法在该平台下性能优化很明显。

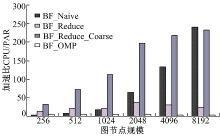
图6 NVIDIA GeForce GTX TITANFig.6 NVIDIA GeForce GTX TITAN

图7为BF_Reduce_Coarse、BF_Reduce、BF_Naive在NVIDIA GeForce GTX 690 GPU平台下的性能加速比, 该平台基于NVIDIA Kepler GK104架构, BF_Reduce_Coarse算法性能优化效果在节点规模小时很明显, 在节点规模比较大时优化性能略比BF_Naive低。

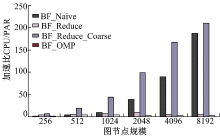
图7 NVIDIA GeForce GTX 690Fig.7 NVIDIA GeForce GTX 690

图8为BF_Reduce_Coarse、BF_Reduce、BF_Naive在AMD Pitcairn GPU平台下的性能加速比, BF_Reduce_Coarse算法性能优化很明显, BF_Reduce在该平台下性能非常低。

图8 AMD Pitcairn GPUFig.8 AMD Pitcairn GPU

实验结果显示:优化后的算法在3个平台下都能很好地实现性能加速, 说明本文提出的优化算法具有很好的性能可移植性, 比CPU串行实现性能平均提高约200~300倍, 比算法OpenMP并行实现性能平均提高约40~80倍, 比BF_Naive并行实现性能平均提高约3~6倍。

另外, 根据实验结果可以发现, 全局内存的访问方式对于算法的性能有很大的影响, 采用矩阵转置方式解决了全局内存访存不连续问题后, 性能有很明显的提高, 提高约4~40倍。当顶点数量达到一定规模时, BF_Reduce_Coarse与BF_Naive在有些平台下加速效果不是很明显, 这是因为当顶点规模比较大时, 需要的线程数比较多, 然而硬件资源是有限的, 而且在并行归约过程中线程组内只有部分线程是有用的, 其他线程一直处于等待状态, 负载不均衡。此外, BF_Reduce_Coarse在归约时需要申请两段共享内存来保存归约过程中间结果, 每个设备只提供数量有限的存储器, 若是每个线程需要的存储空间越大时每个计算单元内驻留的线程数目就越少, 处理的线程也就越少, 会在一定程度上影响性能。从总体性能加速情况来看, 本文对Bellman-Ford算法的优化工作有很重要的意义。

4 结束语

提出了一种面向GPU的性能可移植的并行归约求极值优化算法和全局访存优化算法, 对Bellman-Ford算法进行并行化改造, 并在3个平台下对本文提出的优化方法进行实验。实验结果显示, 优化后算法在多个平台下都能实现很好的性能加速。基于GPU对算法进行优化时, 以下两方面会对算法性能有一定的影响:①Global Memory的访问方式会影响算法的性能, 实验表明, 以对齐方式访问内存可使算法性能提升4~40倍左右。②每个线程需要的存储器数量会在一定程度上影响算法的性能, 主要影响在计算单元上同时驻留的线程数目。

The authors have declared that no competing interests exist.

参考文献
[1] Tehrani Pouya, Zhao Qing. Distributed online learning of the shortest path under unknown rand om edge weights[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, 2013: 3138-3142. [本文引用:1]
[2] Carli M, Panzieri S, Pascucci F. A joint routing and localization algorithm for emergency scenario[J]. Ad Hoc Networks, 2014, 13: 19-33. [本文引用:1]
[3] Tewari A, Kumar D A. Different routing algorithm for computer networks[J]. Kaav International Journal of Science, Engineering & Technology, 2014, 1(1): 21-34. [本文引用:1]
[4] Abouali M, Timmermans J, Castillo J E, et al. A high performance GPU implementation of Surface energy balance system (SEBS) based on CUDA-C[J]. Environmental Modelling & Software, 2013, 41: 134-138. [本文引用:1]
[5] Huang B, Mielikainen J, Oh H, et al. Development of a GPU-based high-performance radiative transfer model for the Infrared atmospheric sounding interferometer (IASI)[J]. Journal of Computational Physics, 2011, 230(6): 2207-2221. [本文引用:1]
[6] Singh D P, Khare N. A study of different parallel implementations of single source shortest path algorithms[J]. International Journal of Computer Applications, 2012, 54(10): 26-30. [本文引用:1]
[7] 颜深根, 张云泉, 龙国平, 等. 基于OpenCL的归约算法优化[J]. 软件学报, 2011, 22(2): 163-171.
Yan Shen-gen, Zhang Yun-quan, Long Guo-ping, et al. Reduction algorithm optimization based on the OpenCL[J]. Journal of Software, 2011, 22(2): 163-171. [本文引用:1]
[8] Kumar S, Misra A, Tomar R S. A modified parallel approach to single source shortest path problem for massively dense graphs using CUDA[C]∥2011 2nd International Conference on Computer and Communication Technology, Allahabod, 2011: 635-639. [本文引用:1]
[9] Lee Jaejin, Kim Jungwon, Seo Sangmin. An OpenCL framework for heterogenous multicores with local memory[C]∥Proceeding of the 19th International Conference on Parallel Architectures and Compilation Techiniques, ACM New York, NY, USA, 2010: 193-204. [本文引用:1]
[10] 贾海鹏, 张云泉, 龙国平, 等. 基于 OpenCL 的拉普拉斯图像增强算法优化研究[J]. 计算机科学, 2012, 39(5): 271-277.
Jia Hai-peng, Zhang Yun-quan, Long Guo-ping, et al. Research on laplace image enhancement algorithm optimization base on OpenCL[J]. Computer Science, 2012, 39(5): 271-277. [本文引用:1]
[11] NVIDIA. NVIDIA's Next Generation CUDA Compute Architecture: Kepler GK110[EB/OL]. [2013-06-28]. http://www.nvidia.com/content/PDF/kepler/NVIDIA-Kepler-GK110-Architecture-Whitepaper.pdf. [本文引用:1]
[12] NVIDIA. NVIDIA's next generation CUDA TM compute architecture, Fermi[EB/OL]. [2013-05-22]. http://www.nvidia.com/content/PDF/fermi_white_papers/NVIDIA_Fermi_Compute_Architecture_Whitepaper.pdf. [本文引用:1]