引用本文
郭玉泉, 李雄飞, 刘昕. 谱分析与启发式遗传算法相结合的多尺度社区检测方法. 2015, 45(5): 1592-1600
GUO Yu-quan, LI Xiong-fei, LIU Xin. Heuristic genetic algorithm associated with spectral analysis uncovering multi-scale community of complex networks. Journal of Jilin University Engineering and Technology Edition, 2015, 45(5): 1592-1600  
Permissions
Copyright©2015, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
谱分析与启发式遗传算法相结合的多尺度社区检测方法
郭玉泉1, 李雄飞1, 刘昕2
1.吉林大学 计算机科学与技术学院,长春 130012
2.吉林大学 网络中心,长春 130022
刘昕(1976-),女,高级工程师.研究方向:智能交通与网络计算.E-mail:lx@jlu.edu.cn

作者简介:郭玉泉(1974-),男,博士研究生.研究方向:复杂网络分析,数据挖掘.E-mail:guoyuquan@sohu.com

基金:吉林省科技发展计划项目(20090468,20100508,201105017)
摘要

针对常规的社区检测方法不能揭示出社区结构的多尺度特征这一问题,本文通过对复杂网络传导率函数C与社区平均凝聚概率的分析,提出了一种局部启发变异策略,同时将复杂网络谱分析与遗传算法相结合,提出了多尺度社区检测算法HGASA。在人工网络和现实网络上对HGASA算法进行了测试,实验结果表明了HGASA算法的有效性和高效性。

关键词: 计算机应用; 多尺度社区; 遗传算法; 启发函数; 局部启发变异算法
中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2015)05-1592-09
Heuristic genetic algorithm associated with spectral analysis uncovering multi-scale community of complex networks
GUO Yu-quan1, LI Xiong-fei1, LIU Xin2
1.College of Computer Science and Technology, Jilin University, Changchun 130012,China
2.Network Center, Jilin University, Changchun 130022,China
Abstract

The community structure of complex networks has attracted much attention. However, previous methods can not investigate the multi-scale property of the community. To address this problem, by analyzing conduct function C and average agglomerate probability, a local heuristic heteromorphosis strategy is proposed; then, spectral analysis of complex networks is combined with genetic algorithm; finally a multi-scale community detection algorithm HGASA (Heuristic genetic algorithm with spectral analysis) is proposed. Extensive tests on artificial networks and real world networks justify the superiority of the HGASA algorithm.

Keyword: computer application; multiple-scale community; genetic algorithm; heuristic function; local heuristic mutation algorithm
0 引 言

目前, 对于网络社区还没有统一定义, 通常认为社区是一个内部连接紧密的节点集合, 而该节点集合与网络的其他部分连接稀疏。在现实网络中, 网络社区表现出多尺度结构特征, 即在不同尺度下有不同的社区划分结果。常用网络社区检测方法可以分为三类:第一类是基于优化的方法, 典型算法有GN[1]、FN[2]、LPAm[3]和LGA[4]方法。优化方法多以Newman等[5]提出的Q函数为优化目标, 而最大化Q函数是NP完全问题, 所以这些优化算法都是近似的优化算法。第二类是层次聚类方法, 典型算法有EAGLE[6]和CPM[7]。层次聚类方法中树状图生成与分割的时间复杂度都很高, 因此层次聚类方法效率较低。第三类是网络动力学方法, 如Jin等[8]提出的基于马尔可夫方法的社区检测方法。以上方法多数都是单一尺度的网络社区结构检测, 不能检测多尺度网络社区结构。网络社区结构的多尺度特征是通过网络传播特性与谱特征来体现的, 目前检测都是采用基于网络动力学与谱方法的检测算法。Alex等[9]利用同步过程与拉普拉斯矩阵谱检测多尺度社区; Delvenne等[10]通过在时间尺度上社区稳定性检测多尺度社区; Cheng等[11]通过复杂网中传播过程的稳定状态检测多尺度社区。

为评估社区检测结果的优劣, 2004年Newman[5]提出了网络社区的度量标准, 称为模块化函数。随着研究的深入, Fortunato[12]、Arenas[13]等发现模块化函数存在分辨率限制(Resolution limit), 无法发现特定尺寸的社区结构。2010年, Cheng等[11]提出的传导率函数(C函数)作为网络社区评价标准, 传导率函数从网络动力学角度评价网络社区划分结果, 克服了模块化函数的分辨率限制问题。

本文提出的HGASA算法(Heuristic genetic algorithm with spectral analysis, HGASA)通过谱分析获得复杂网络多尺度结构信息, 将结构信息应用于遗传算法优化过程。算法从网络动力学角度分析了个体变异过程, 提出基于网络动力学的变异操作启发函数, 用于指导变异操作, 同时证明该启发函数与优化目标函数(C函数)存在单调关系。

1 谱分析

矩阵的谱特性已经被广大学者深入研究, 将其应用到复杂网络社区检测中时, 可以根据复杂网络矩阵的谱特性揭示出复杂网络的社区结构[14]。复杂网络通常使用图G=(V, E)来描述, 其中V表示网络的节点集合, E表示网络中边的集合。邻接矩阵是图的主要表示方法, 当使用邻接矩阵A描述图时, Aij定义如下:

Aij=1, 当节点i与节点j之间有边0, 当节点i与节点j之间无边1

邻接矩阵有多种扩展形式, 如标准拉普拉斯矩阵、规范化拉普拉斯矩阵、模块化矩阵、关联矩阵。本文只讨论无权重无向网络, 采用规范化拉普拉斯矩阵[14]用于社区结构检测。规范化拉普拉斯矩阵定义为N=I-T, 其中I为单位阵, T=D-1A, D为对角阵, Dii为节点i的度, A为网络邻接矩阵。

定义1 假设λ 1, …, λ n是规范化拉普拉斯矩阵N的n个特征值, 将特征值按递增排序并去除重复的特征值得到一个递增序列ω 1, …, ω m(m< n), 称此序列为矩阵N的谱, 记为S(N)={ω 1, …, ω m}。

定义2 S(N)为规范化拉普拉斯矩阵N的谱, 设ei=ω i+1-ω i, 则ei称为矩阵N的第i个谱隙。

设定一个阈值ep, 当谱隙大于此阈值(即ei> ep)时, 认为ei是一个有效谱隙, 实际应用中ep取值0.5[15]。将矩阵N的有效谱隙按递减顺序排列, 每个谱隙对应一个社区尺度, 谱隙的下标值与网络中社区的数量一致, 由此得到了复杂网络的多尺度社区结构。多尺度社区结构反映了网络在传播过程中的动力学特征[11], 矩阵的谱分析方法可以有效地揭示出网络的社区结构。

算法1 多尺度社区结构的算法

Input:网络邻接矩阵A, 谱隙阈值ep, 输出列表中元素的数量m

Output:社区数量值列表L

1 T=D-1A

2 N=I-T

3 计算N的特征值λ 1…λ n;

4 计算N的谱隙e1…en-1;

5 对大于阈值ep的谱隙按递减进行排序, 得到谱隙序列EP;

6 取EP中前m个元素的下标值放入到L中;

7 Return

2 HGASA算法

2.1 编解码

HGASA算法采用字符串编码方式[16], 每个字符串代表一个个体, 每个字符位置代表节点, 每个字符代表节点所属的社区。Ii=(Li1, Li2, …, Lin), Ii表示第i个个体, Lin表示第i个个体中第n个基因表达, 这里表示节点n的社区标识符。由上面的定义知, 如果Lip=Liq, 则表明Ii所对应的社区结构中, 节点p与节点q在同一个社区中。

2.2 群体初始化

遗传算法在群体初始化时通常采用随机生成个体的方式, 这样可以使初始群体具有多样性。HGASA算法中采用标签传播[17]方法生成个体, 初始时个体每个节点分配一个社区标识符, 然后经过数次异步标签传播产成个体。标签传播方法的随机性保障生成个体的多样性, 同时具有很高的效率。但是标签传播方法生成个体的社区结构具有不确定性, 使个体需要较长的进化时间才能达到目标状态。标签传播算法生成的个体虽然具有一定的社区结构, 但与社区检测的目标有一定的差距。HGASA算法利用矩阵谱分析的结果作为标签传播的约束条件, 在标签传播过程中控制个体中标签的数量与谱分析的结果一致, 这样个体生成时便具有了基本的社区结构, 从而保障后续优化过程的效率和精度。

算法2 群体初始化算法

Input: 个体包含社区的数量k, 群体包含个体的数量m

Output: 群体p

1 for i=1 to m

2 生成个体I;

3 While(个体I社区标识数量> k)

4 随机选择个体I的一个基因位置, 进行标签传播操作;

5 将I加入到群体p中;

6 Return p

2.3 交叉操作

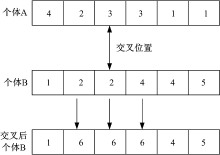
采用遗传算法解决社区检测问题时, 交叉操作中有一定的特殊性, 进行交叉操作时要将一组关联密切的基因交叉给下一代而不是个别基因, 因此, 不能采用传统的单点、多点交叉方法, 而是采用单路交叉、多路交叉。本文对Tasgin[16]提出的单路交叉算法进行了改进, 称为合并式单路交叉(One-way incorporating crossing)。改进的目的是使交叉后新个体保留两个父母个体交叉位置的最大社区结构特征。合并式单路交叉操作过程定义如下:设A、B是任意两个体, A作为源个体, B作为目的个体, CB(n)为个体B中节点n所属社区的节点集合, CA(n)为个体A中与节点n在同一社区节点的集合, L为初始状态(每个节点一个社区)社区标识符的集合, L(B)为个体B中社区标识符的集合, LB(n)为个体B中节点n的社区标识符。进行交叉操作时, 首先在个体A中选择一个节点作为交叉位置, 设节点n被选为交叉位置; 然后, 在个体B中所有包含于CB(n)∪ CA(n)中的节点进行交叉操作, 对每个节点取一个不同于个体B中现有标签进行赋值, 即LB(m)← L∀ m∈ CB(n)∪ CA(n)且L{L-LB}。

交叉操作如图1所示。在交叉后个体B中标签6所代表的社区结构继承了个体A与个体B的结构特征。

图1 交叉操作Fig.1 Cross operation

合并单路交叉能保留上一代个体的社区结构特征, 在新个体中社区结构特征更加突出。

2.4 变异操作

对于复杂网络社区检测问题, 遗传算法通常采用随机方式变异, 变异操作缺乏必要的启发信息, 对于变异操作的进化方向缺乏有效控制, 从而使个体进化速度缓慢, 优化效果不佳。基于上述原因, 遗传算法难以应用于大规模网络的社区检测。本节针对复杂网络社区检测过程, 构建了局部动力学启发函数, 以启发变异操作进化方向, 并且证明启发函数和HGASA算法目标函数单调, 从而提高个体进化速度和检测精度。

HGASA算法采用传导率函数C(P)作为目标函数, 其定义如下:

C(P)=1k∑i=1k1-in_vol(Vi)vol(Vi)2

式中:P为复杂网络的一个社区检测结果, P={V1, …, Vk}, 其中k为社区个数, Vi表示第i个社区中的节点集合。

定义3 社区Vi的内部度in_vol(Vi)定义为in_vol(Vi)= ∑x∈Vi, y∈ViAxy。

定义4 社区Vi的度vol(Vi)定义为vol(Vi)= ∑x∈Vi, yAxy。

从传导率定义(式(2))可以看出, 传导率是每个社区分离概率的平均值, 反映了复杂网络中社区间传播的能力, 体现了复杂网络的一种动力学特征。传导率越小, 社区结构划分越合理。

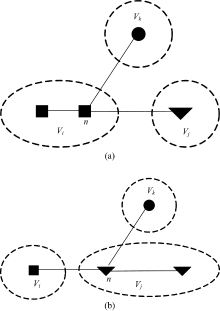
命题1 n是一个节点, C是一个社区, n∉C, n与C中节点存在一条边, 当节点n社区标识符由l变化为l'时, 社区C的内部度in_vol(C)不变化。

证明 如图2所示, 在图2(a)中, n∈ Vi, 节点n与社区Vk中某一节点间存在一条边。当节点n由社区Vi划分到Vj后, 即Vi-{n}, Vj+{n}, 如图2(b)所示, 社区Vk的内部度与外部度都没有变化, 所以命题1成立, 证毕。

图2 节点社区变化示意图Fig.2 Community of node

命题1阐明了节点社区标识变化和其相邻社区内部度的关系, 在变异操作中性质1表现为将一个节点由包含它的当前社区分离, 然后融入到与节点连接更紧密的相邻社区。从网络动力学角度分析此过程, 可以认为是“ 社区标识符” 从邻居社区传递到当前节点过程, 即节点i的社区标识符由L(V(i))变为L(V(j)), 其中L(V(i))表示包含节点i的社区, L(V(i))表示节点i的社区标识符。由于社区标识符传播导致复杂网络社区划分的传导率发生变化。社区标识符由一个社区传播到相邻社区边缘节点时连接两个社区间边的数量发生变化, 因此引入函数h(Ci, Cj)(简称h函数)评估两个社区之间社区标识符的传播能力, 其定义如下:

h(Ci, Cj)=12in_vol(Ci)vol(Ci)+in_vol(Cj)vol(Cj)3

式中:Ci、Cj代表两个相邻的社区。

h(Ci, Cj)函数代表两个相邻社区的凝聚概率的平均值。当社区标识传播达到稳定状态时, 社区标识符所表达的社区结构是网络的社区结构。

命题2 当社区数量不变时, 传导率函数C(P)与h(Vi, Vj)单调递减, P为一个分区, Vi、Vj为相邻的社区, Vi∈ P, Vj∈ P, P={V1, …, Vk}。

证明 设P为一个社区划分, P={V1, …, Vk}, 节点n∈ Vi。社区标识符通过网络传播, 节点n当前标识符为L(Vi), 当社区标识符L(Vj)传播至节点n时, 引发社区划分由P变为P', P'={V'1, …, V'k}。社区标识符L(Vj)传播到节点n后引起的

函数h的增量如下:

Δhn=h(V'i, V'j)-h(Vi, Vj)=12in_vol(V'i)vol(V'i)+in_vol(V'j)vol(V'j)-12in_vol(Vi)vol(Vi)+in_vol(Vj)vol(Vj)=12in_vol(Vi-{n})vol(Vi-{n})+in_vol(Vj+{n})vol(Vj+{n})-in_vol(Vi)vol(Vi)-in_vol(Vj)vol(Vj)

由n的社区标识变化引起的传导率函数C(P)的增量如下:

ΔC=C(P')-C(P)=1k∑i=1k1-in_vol(V'i)vol(V'i)-1k∑i=1k1-in_vol(Vi)vol(Vi)

根据命题1除社区Vi与Vj外其他社区有in_vol(V'i)=in_vol(Vi), 于是有:

ΔC=1kin_vol(Vi)vol(Vi)+in_vol(Vj)vol(Vj)-in_vol(V'i)vol(V'i)-in_vol(V'j)vol(V'j)=1kin_vol(Vi)vol(Vi)+in_vol(Vj)vol(Vj)-in_vol(Vi-{n})vol(Vi-{n})-in_vol(Vj+{n})vol(Vj+{n})=-2kΔhn

综上所述, C(P)与h(Ci, Cj)单调递减, 命题2成立。需要特别说明的是, 命题2中在社区标识符传递的过程中不讨论社区标识符减少的情况, 因为这种情况不满足优化目标的要求。

从命题2可知:传导率函数C(P)与函数h(Vi, Vj)单调递减, 因此使用h(Vi, Vj)作为社区标识符传播的启发信息, 当社区标识符向着h(Vi, Vj)增大的方向传播时, C(P)将变小, 此时得到的社区结构更优良。

当社区标识符在网络上传播时, 它到达的下一个节点与它在同一社区的概率最大。基于此本文提出如下的变异方法:对于个体I的第i个基因(即节点i被选择进行变异), 节点i的邻接社区标识符集合为Ln(i), 只需在Ln(i)中选择一个社区标识符, 不需要考虑节点i的所有邻居节点的社区标识符, 而是以h(Vi, Vj)作为启发函数, 选择具有最大h值的标签传播到当前节点。Li← arg maxL{h(Vi, VL) L∈ Ln(i)}。Li为节点i的社区标识符。

算法3 基于h函数的局部启发式变异算法(Local heuristic mutation algorithm, LHMA)

Input: 待变异个体Ind, 变异基因位置Pos

Output: 变异后个体Ind

1 for k=1 to n //n为节点数量

2 List =NeiLabel(pos, Ind) //求节点相邻社区标识符集合

3 m=length(List) //计算队列长度

4 for i =1 to m

5 t=h(Vpos, VList[i]) //计算h函数

6 if (t> max_h)

7 max_h=t

8 L=Label(VList[i])

9 将Ind中pos位置基因变为L

10 Return Ind

性质1 LHMA的时间复杂度为O(Cn)。

证明 假设网络的社区数量为k, 节点的平均外度为dout, 网络节点数量为n, 对于个体I发生变异节点的概率为β 。

设计算h函数的平均时间为t, 每个节点直接相连外部社区数量为dout, 则每个节点计算所有h函数的时间的最大值为O(doutt), 总的时间复杂度为O(β douttn)。将tdoutβ 看作常数C, 则LHMA的时间复杂度为O(Cn)。

2.5 HGASA框架

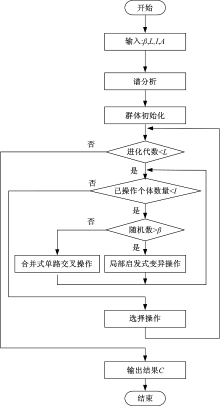
HGASA的流程图如图3所示。算法首先对复杂网络的拉普拉斯矩阵进行谱分析, 得到不同尺度下复杂网络的社区数量; 然后根据社区数量进行群体初始化, 得到具有特定尺度社区结构的个体; 最后使用局部启发式变异算法与合并式单路交叉算法对群体进行优化, 从而得到复杂网络的社区结构。HGASA算法选择在所有个体进行完交叉或变异操作后进行, 将交叉和变异产生的新个体加入群体中, 然后在新群体中选择传导率最小的个体作为下一代种群。

图3 HGASA算法流程图Fig.3 Flow diagram of HGASA

算法4 HGASA

Input:邻接矩阵A, 变异概率β , 进化代数L, 种群数量I

Output: 为社区检测结果C

1 spectrumanalysis (A) //对矩阵进行谱分析

2 Initialization() //群体初始化

3 While(进化代数< L)

4 for i=1 to I

5 If rand()> β

6 LHMA(); //局部启发式变异算法

7 Else

8 OWICA(); //合并式单路交叉算法

9 Select(); //选择操作

10 C← 社区检测结果

11 Return C

性质2 HGASA算法的时间复杂度为O(Mn)。

证明 步骤1的时间复杂性为O(kn)。步骤2对于每个个体经2~3次的标签传播可以得到满足要求的个体, 步骤2时间复杂性为O(2In), 步骤5至步骤8时间复杂度为O(Lβ Cn)。所以HGASA算法时间复杂度为O(kn+2In+Lβ Cn), 即O((k+2I+Lβ C)n), 设k+2I+LC=M, 所以算法时间复杂度为O(Mn)。

3 实 验

采用人工网络和现实网络对HGASA的性能进行测试。算法采用VC++6.0、Matlab7.0在Windows XP下实现。VC++ 6.0实现遗传算法部分, Matlab7.0实现矩阵分析。

HGASAd的主要参数有5个, 群体规模I、进化代数G、个体变异概率α 、个体基因发生变异的概率β 和隙阈值ep。前四个参数是遗传算法常用参数。第五个参数是用于控制谱隙的有效值, 一般取0.5。实验采用召回率和精度来比较不同算法的分区结果。

3.1 人工网络

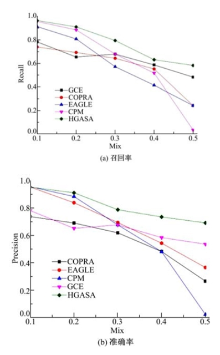
目前人工生成网络方法有多种, 本文采用Lancichinetti[18]提出的方法进行人工网络生成。这种方法可以根据节点的度、社区尺寸等多种方式生成社区, 使生成的网络能够更深入地检查社区检测方法的性能。混合率Mix(0≤ Mix≤ 1)是Lancichinetti方法控制网络生成的重要参数, 它反映了社区结构的清晰程度, Mix越小网络社区结构越清晰, 反之社区结构模糊。选择GCE[19]、CPM[7]、COPRA[17]、EAGALE[6]作为对比算法。从图4可以看出:0.1≤ Mix≤ 0.2时, 网络社区结构明显, 对比算法和HGASA都有较高的召回率和准确率, 随着Mix增大网络社区结构变得模糊, 对比算法的准确率和召回率显著降低, 但HGASA仍可较好地发现社区结构, 说明HGASA在检测模糊社区结构方面性能明显优于对比算法。

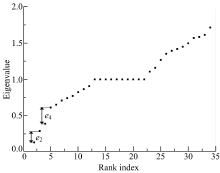
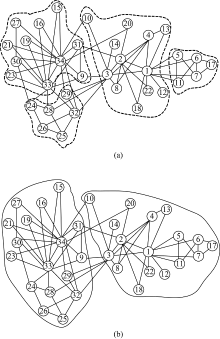
图4 HGASA算法的召回率和准确率Fig.4 Recall rate and precision of HGASA

3.2 现实网络

HGASA对现实世界网络的检测选用空手道俱乐部网络和海豚网络来进行。空手道俱乐部网络(Karate)[20]展示了美国一所大学空手道俱乐部34名成员间的社会关系, 每个节点代表一名成员, 两个节点间有一条边则意味着相应的两个成员之间是交往频繁的朋友关系。用HGASA对空手道俱乐部网络进行检测的结果如图5、图6所示。图5是空手道俱乐部网络的谱隙, e2、e4是两个谱隙, 对应的社区数量为2和4。图6为HGASA对空手道俱乐部网络的检测结果, 此社区结构与现实观察的检测结果一致。通过实验可

以看到HGASA可以有效地检测出Karate的多尺度社区结构。

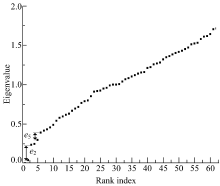
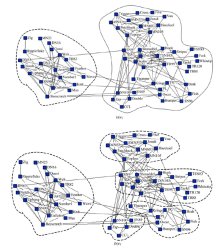
图5 Karate网络谱隙Fig.5 Spectral of Karate

图6 Karate网络的多尺度社区结构Fig.6 Multiple-scale community structure of Karate

海豚网络[21]是Lusseau通过对新西兰神奇湾中62只不同性别海豚观测而构建的动物社会网。网络中每个节点代表一只海豚, 如果两个海豚联系密切, 那么海豚对应的顶点之间就会有一条边连接。这些海豚被天然地分为雄性海豚组和雌性海豚组两个社区。由图7可以看到海豚网络的e2、e5对应两个社区结构。图8(a)为海豚网络对应e2的社区结构, 海豚网络被分成两个大的社区, 图8(b)为海豚网络对应e5的社区结构, 可以看到在图8(a)中右侧社区又被细分为4个社区。

图7 海豚网络谱隙Fig.7 Spectra of dolphin

通过在人工网络和现实网络上对HGASA的测试可以看出, HGASA具有较强的社区检测能力, 在社区结构不明显时仍有较好的检测结果, 并且可以有效地检测出多尺度网络社区结构。

图8 海豚网络多尺度社区结构Fig.8 Multiple-scale community structure of dolphin

4 结束语

利用矩阵谱分析方法揭示出复杂网络的多尺度特征, 并且结合局部网络动力学启发函数提出了遗传算法HGASA。计算机生成网络和现实网络的测试结果表明, HGASA可有效地检测多尺度网络社区结构。在后续的研究中, 作者将进一步研究多尺度社区结构与网络功能演化的关系。

The authors have declared that no competing interests exist.

参考文献
[1] Girvan M, Newman M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(12): 7821-7826. [本文引用:1]
[2] Newman M E J. Fast algorithm for detecting community structure in networks[J]. Physical Review E, 2004, 69(6): 066133. [本文引用:1]
[3] Barber M J, Clark J W. Detecting network communities by propagating labels under constraints[J]. Physical Review E, 2009, 80(2): 026129. [本文引用:1]
[4] Liu D Y, Jin D, Baquero C, et al. Genetic algorithm with a local search strategy for discovering communities in complex networks[J]. International Journal of Computational Intelligence Systems, 2013, 6(2): 354-369. [本文引用:1]
[5] Newman M E J. Detecting community structure in networks[J]. European Physical Journal B, 2004, 38(2): 321-330. [本文引用:2]
[6] Shen H W, Cheng X Q, Cai K, et al. Detect overlapping and hierarchical community structure in networks[J]. Physica A: Statistical Mechanics and Its Applications, 2009, 388(8): 1706-1712. [本文引用:2]
[7] Palla G, Derenyi I, Farkas I, et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature, 2005, 435(7043): 814-818. [本文引用:2]
[8] Jin D, Yang B, Baquero C, et al. A Markov rand om walk under constraint for discovering overlapping communities in complex networks[J]. Journal of Statistical Mechanics-Theory and Experiment, 2011(5): P05031. [本文引用:1]
[9] Alex Arenas, Albert Diaz-Guilera, Conrad J. Synchronization reveals topological scales in complex networks[J]. Physical Review Letters, 2006, 96(11): 114102. [本文引用:1]
[10] Delvenne J C, Yaliraki S N, Barahona M. Stability of graph communities across time scales[J]. Proceedings of the National Academy of Sciences, 2010, 107(29): 12755-12760. [本文引用:1]
[11] Cheng X Q, Shen H W. Uncovering the community structure associated with the diffusion dynamics on networks[J]. Journal of Statistical Mechanics-Theory and Experiment, 2010(4): P04024 [本文引用:3]
[12] Fortunato S, Barthelemy M. Resolution limit in community detection[J]. Proceedings of the National Academy of Sciences, 2007, 104(1): 36-41. [本文引用:1]
[13] Arenas A, Fernand ez A, Gomez S. Analysis of the structure of complex networks at different resolution levels[J]. New Journal of Physics, 2008, 10(5): 053039. [本文引用:1]
[14] Shen H W, Cheng X Q. Spectral methods for the detection of network community structure: a comparative analysis[J]. Journal of Statistical Mechanics-Theory and Experiment, 2010(10): P10020 [本文引用:2]
[15] Shen H W, Cheng X Q, Wang Y Z, et al. A dimensionality reduction framework for detection of multiscale structure in heterogeneous networks[J]. Journal of Computer Science and Technology, 2012, 27(2): 341-357. [本文引用:1]
[16] Tasgin M, Herdagdelen A, Bingol H. Community detection in complex networks using genetic algorithms[EB/OL]. [2013-07-08] . http://arxiv.org/abs/0711.0491. [本文引用:2]
[17] Gregory S. Finding overlapping communities in networks by label propagation[J]. New Journal of Physics, 2010, 12(10): 103018 [本文引用:2]
[18] Lancichinetti A, Fortunato S, Radicchi F. Benchmark graphs for testing community detection algorithms[J]. Physical Review E, 2008, 78(4): 046110. [本文引用:1]
[19] Lee C, Reid F, Mcdaid A, et al. Detecting highly overlapping community structure by greedy clique expansion[EB/OL]. [2013-09-22]. http://arxiv.org/abs/1002.1827. [本文引用:1]
[20] Zachary W. An information flow modelfor conflict and fission in small groups1[J]. Journal of Anthropological Research, 1977, 33(4): 452-473. [本文引用:1]
[21] Lusseau D. The emergent properties of a dolphin social network[J]. Proceedings of the Royal Society of London Series B: Biological Sciences, 2003, 270(Suppl 2): 186-188. [本文引用:1]