LTE中DRX节能策略的系统建模及性能优化

引用本文

王志衡, 霍占强, 金顺福. LTE中DRX节能策略的系统建模及性能优化. 2015, 45(5): 1615-1623
WANG Zhi-heng, HUO Zhan-qiang, JIN Shun-fu. System modeling and performance optimization for the power saving strategy of DRX in LTE. Journal of Jilin University Engineering and Technology Edition, 2015, 45(5): 1615-1623 复制到剪切板

Permissions

LTE中DRX节能策略的系统建模及性能优化

王志衡¹, 霍占强¹, 金顺福²

1.河南理工大学计算机科学与技术学院,河南焦作 454000

2.燕山大学信息科学与工程学院,河北秦皇岛 066004

霍占强(1979-),男,副教授,博士.研究方向:网络通信技术.E-mail:hzq@hpu.edu.cn

作者简介:王志衡(1983-),男,副教授,博士.研究方向:图像处理技术,数学建模及优化方法.E-mail:wzhenry@eyou.com

基金:国家自然科学基金项目(61472342)

摘要

兼顾LTE(Long term evolution)通信技术中移动终端的节能效果和响应速度,提出了一种带有休眠延迟机制的非连续接收DRX(Discontinuous reception)节能策略。考虑到网络中实际缓存容量的有限性,建立了一个带有休假延迟和启动阶段的多重休假有限容量排队模型,综合使用嵌入Markov链方法和补充变量的方法,导出系统阻塞率、能量节省率和数据帧延迟等指标表达式。结合数值实验和仿真实验,揭示了不同指标之间的折衷关系。对DRX中的休眠延迟器长度和系统容量大小进行了优化设置,为无线通信网络节能策略的改进及优化提供了理论依据。

关键词: 计算机应用; LTE; 节能策略; 休眠延迟; 多重休假排队

中图分类号:TP393 文献标志码:A 文章编号:1671-5497(2015)05-1615-09

System modeling and performance optimization for the power saving strategy of DRX in LTE

WANG Zhi-heng¹, HUO Zhan-qiang¹, JIN Shun-fu²

1.College of Computer Science and Technology, He'nan Polytechnic University, Jiaozuo 454000, China

2.School of Information Science and Engineering, Yanshan University, Qinhuangdao 066004, China

Abstract

In order to reduce the energy consumption and increase the response speed of the mobile stations in Long Term Evolution (LTE) communication technology, a novel power saving strategy is proposed in Discontinuous Reception (DRX) with sleep-delay mechanism. Considering that the system buffer is finite in practice, a multiple-vacation queuing model with a sleep-delay period and a waking-up procedure is built. Using the methods of embedded Markov chain and supplemental variable, the formulas of the system block ratio, the energy saving ratio and the latency of data frames are given. Combining the numerical experiments with analysis and simulation, the trade-off between different performance measures is investigated. Finally, the time length of the sleep-delay period and the buffer capacity in DRX are optimized. The results of this research have potential applications in the improvement and optimization of the energy saving strategy in wireless communication networks.

Keyword: computer application; LTE; power saving strategy; sleep-delay; multiple vacation queueing model

Show Figures

0 引言

网络规模的扩大和网络设备的更新加快了网络演进, 寻找新型的网络架构和空中接口技术, 成为网络发展的必然趋势。然而, 目前的网络应用日益暴露出能耗高、效率低、浪费多等诸多问题^{[1, 2]}。长期演进技术LTE(Long term evolution)作为第三代合作伙伴计划3GPP(the 3rd generation partner project)标准, 从通用移动通信系统UMTS(Universal mobile telecommunications system)技术衍生而来, 也称为4G标准^{[3, 4]}。LTE重新定义了核心网络和空中接口技术, 采用正交频分复用技术和多输入多输出作为其无线网络演进的唯一标准, 改善了小区边缘用户的性能, 提高了小区容量, 并降低了系统延迟。同时, LTE引入了一种非连续接收DRX(Discontinuous reception)省电工作机制^[5]。

近年来, 研究人员对移动通信系统中节能策略进行了相关研究。文献[6]假设UMTS中的DRX参数服从泊松分布, 利用半马尔科夫过程对DRX节能策略进行了建模分析, 通过系统实验研究了DRX的系统参数对平均分组时延和功率节省等性能指标的影响。文献[7]将LTE网络中的DRX节能策略的运行过程与载波聚合CA(Carrier aggregation)技术相结合, 基于Markov过程和排队理论, 结合系统实验, 分析并比较了不同的DRX参数设置和CA载体组件配置对系统性能的影响。文献[8]引入了一种轻度休眠模式以进一步提高LTE网络中DRX的节电性能, 关键思想是在系统快速苏醒过程中, 关闭能量放大器, 减少能量消耗。

已有的有关DRX节能策略及性能研究的工作, 或者是在策略改进中专注于系统的能量节省效果, 或者是在性能分析中假设系统容量是无穷大的。本文兼顾LTE中移动终端的节能效果和响应速度, 引入休眠延迟机制, 提出一种新的DRX节能策略。基于有限容量排队场所, 建立一个多重休假排队模型, 结合系统实验, 进行DRX节能策略的性能分析与系统优化。

1 DRX节能策略及系统模型

LTE中的DRX节能策略, 定义在媒体访问控制MAC(Media access control)子层, 按照工作状态分为空闲状态DRX(IDLE DRX)和连接状态DRX(ACTIVE DRX)^{[9, 10, 11]}。IDLE DRX是指用户终端UE(User equipment)处于IDLE状态下的DRX, 当缓冲区中没有数据帧时, 系统处在空闲状态, UE不必监听物理下行信道PDCCH(Physical downlink control channel)的信息; 如果有数据帧到达, UE发送一个无线资源控制协议RRC(Radio resource control)请求, 与基站eNB(Evolved nodeB)重新建立一个空口连接^[12], 启动监听PDCCH。而另一种ACTIVE DRX, 是指UE处在连接状态的DRX, 当没有数据帧到达时, UE不必持续监听PDCCH, 同时会临时关闭传输单元以节约能量; 当有数据帧到达时, 由于系统在这个状态下依然存在RRC连接, UE不需要和eNB重新建立空口连接, 便可启动监听PDCCH, 迅速转到工作状态, 因此可以减少信令开销, 加快传输速度^[13]。

本文在传统的DRX节能策略中引入一个休眠延迟定时器。当缓存清空后, 首先启动休眠延迟定时器。如果在休眠延迟定时器超时之前有数据帧到达, 系统立即转入工作状态进行数据传输; 否则, 系统在定时器超时后转入休眠状态, 开始一个短休眠间隔。如果在一个短休眠间隔内没有数据帧到达, 且短休眠间隔的数量未达到规定阈值, 则开始下一个短休眠间隔; 如果在短休眠间隔内没有数据帧到达, 但是短休眠间隔的数量达到阈值M, 系统将进入长休眠间隔。如果在某一长休眠间隔内没有数据帧到达, 则在该休眠间隔结束之后, 开始另一个长休眠间隔; 否则, 系统将从休眠状态返回工作状态。

显然, 过大的休眠延迟定时器长度将影响系统的节能效果, 而过小的休眠延迟定时器长度又会使系统在休眠状态与工作状态之间频繁切换, 达不到减少网络开销及降低响应延迟的目的。系统缓存的大小和休眠延迟定时器的长短是关乎本文所提出的改进的DRX节能策略是否可行的重要因素。因此, 需要通过数学方法定量分析休眠策略的系统性能并优化设计策略相关的系统参数。

将连续传输数据的过程抽象为忙期B, 从一个忙期开始时刻到下一个忙期开始时刻为止的时间抽象为忙循环R。将改进的DRX节能策略中的休眠延迟阶段抽象为休假延迟期D。将每个短休眠间隔抽象为短休假期V₁, 长休眠间隔抽象为长休假期V₂, 将连续的若干短休假期V₁和长休假期V₂统一抽象为系统休假期V。将数据信道的激活过程抽象为启动期U, 系统缓存抽象为排队场所。本文所提出的改进的DRX休眠策略可以建模为一个带有休假延迟期和启动期的多重休假期排队系统。

2 系统模型的解析

设一个忙期B的长度为T_B; 一个休假延迟期D的最大长度, 即定时器长度为T, 实际长度为T_D; 一个短休假期和长休假期的长度分别为 $\begin{matrix} T_{V_{1}} \end{matrix}$ 和 $\begin{matrix} T_{V_{2}} \end{matrix}$ , 一个系统休假期V的长度为T_V; 启动期的长度为T_U。同时, 设短休假期数量阈值为M, 系统所能容纳的最大数据帧数, 即系统容量为K(K< ¥ )。

将时间轴分割为长度相等的时间间隔, 称为“ 时隙” , 令数据帧的到达和离去只发生在时隙的边界处。考虑单个信道, 有限容量为K, 令数据帧的传输采用先到先服务的排队规则。

假设数据帧的到达间隔{J_n, n≥ 1}是独立同分布(i.i.d.)的随机变量, J_n服从参数为p的几何分布, 即P $\begin{matrix} \{J_{n} = k\} \end{matrix}$ = $\begin{matrix} {\bar{pp}}^{k - 1} \end{matrix}$ , k=1, 2, …, 其中0< p< 1, $\begin{matrix} \bar{p} \end{matrix}$ =1-p。假设数据帧的传输时间{S_n, n≥ 1}也是i.i.d.的随机变量, S_n服从一般分布, 其概率分布、均值及母函数分别为:s_k=P{S_n=k}, k=1, 2, …; E[S_n]=b; S(z)= $\begin{matrix} \overset{\infty}{\sum_{k = 1}} \end{matrix}$ s_kz^k。

2.1 各阶段的时间长度及到达的数据帧个数

一个休假延迟期D的实际长度T_D可能是一个休假延迟期D内有数据帧到达条件下的到达间隔, 也可能是一个完整的定时器长度T。休假延迟期D的实际长度T_D的均值为:

$\begin{matrix} E [T_{D}] = \frac{1 - {\bar{p}}^{T}}{p} (1) \end{matrix}$

式中: $\begin{matrix} {\bar{p}}^{T} \end{matrix}$ 表示在休假延迟期D内没有数据帧到达, 系统从D进入系统休假期V的概率。一个忙循环内, 系统休假期V的长度的均值为:

$\begin{matrix} E [T_{V}] = {\bar{p}}^{T} (\frac{P_{V_{1}} T_{V_{1}}}{1 - {\bar{p}}^{T_{V_{1}}}} + \frac{P_{V_{2}} T_{V_{2}}}{1 - {\bar{p}}^{T_{V_{2}}}}) (2) \end{matrix}$

式中: $\begin{matrix} P_{V_{1}} \end{matrix}$ =1- $\begin{matrix} {\bar{p}}^{M T_{V_{1}}} \end{matrix}$ 表示系统从一个短休假期V₁进入启动期U的概率; $\begin{matrix} P_{V_{2}} \end{matrix}$ = $\begin{matrix} {\bar{p}}^{M T_{V_{1}}} \end{matrix}$ 表示系统从一个长休眠期V₂进入启动期U的概率。

在一个忙循环R内, 启动期U存在的概率为 $\begin{matrix} {\bar{p}}^{T} \end{matrix}$ , 由此得U长度的均值为:

$\begin{matrix} E [T_{U}] = {\bar{p}}^{T} T_{U} (3) \end{matrix}$

一个短休假期V₁内有i个数据帧到达的概率为:

$\begin{matrix} A_{_{i}}^{V_{1}} = (\begin{matrix} T_{V_{1}} \\ i \end{matrix}) p^{i} {\bar{p}}^{T_{V_{1}} - i}, 0 \leq i \leq T_{V_{1}} \end{matrix}$

一个长休假期V₂内有i个数据帧到达的概率为:

$\begin{matrix} A_{_{i}}^{V_{2}} \end{matrix}$ = $\begin{matrix} (\begin{matrix} T_{V_{2}} \\ i \end{matrix}) \end{matrix}$ pⁱ $\begin{matrix} {\bar{p}}^{T_{V_{2}} - i} \end{matrix}$ , 0≤ i≤ $\begin{matrix} T_{V_{2}} \end{matrix}$

一个启动期U内有i个数据帧到达的概率为:

$\begin{matrix} A_{i}^{U} \end{matrix}$ = $\begin{matrix} (\begin{matrix} T_{U} \\ i \end{matrix}) \end{matrix}$ pⁱ $\begin{matrix} {\bar{p}}^{T_{U} - i} \end{matrix}$ , 0≤ i≤ T_U

一个数据帧的传输时间S内有i个数据帧到达的概率及其PGF分别表示为:

$\begin{matrix} A_{i}^{S} \end{matrix}$ = $\begin{matrix} (\begin{matrix} k \\ i \end{matrix}) \end{matrix}$ pⁱ $\begin{matrix} {\bar{p}}^{k - i} \end{matrix}$ s_k, i=0, 1, …

$\begin{matrix} A_{i}^{S} \end{matrix} \begin{matrix} (z) \end{matrix}$ = $\begin{matrix} \overset{\infty}{\sum_{i = 1}} \end{matrix} \begin{matrix} \overset{i}{\sum_{k = 0}} \end{matrix}$ z^k $\begin{matrix} (\begin{matrix} i \\ k \end{matrix}) \end{matrix}$ p^k $\begin{matrix} {\bar{p}}^{i - k} \end{matrix}$ s_i=S $\begin{matrix} (\bar{p} + pz) \end{matrix}$

2.2 系统的实际负载

考虑晚到系统, 选择系统忙期开始的时刻和每个数据帧完成传输的时刻作为嵌入点, 并由嵌入点处的数据帧个数表示系统的状态。忙期开始时刻及数据帧完成传输离去后, 系统中有k(1≤ k≤ K)个数据帧的概率分别由q_k和Q_k表示。

(1)当k=1时, 忙期开始时刻系统中的数据帧可能在休假延迟期、短休假期、长休假期中的任一时间段到达, 其概率分布为:

$\begin{matrix} q_{1} = Q_{0} (1 - {\bar{p}}^{T} + {\bar{p}}^{T} (\frac{P_{V_{1}} A_{1}^{V_{1}}}{1 - {\bar{p}}^{T_{V_{1}}}} + \frac{P_{V_{2}} A_{1}^{V_{2}}}{1 - {\bar{p}}^{T_{V_{2}}}}) A_{0}^{U}) (4) \end{matrix}$

(2)当2≤ k≤ K-1时, 忙期开始时刻的数据帧可能在短休假期及其之后的启动期到达, 或者在长休假期及其之后的启动期到达, 其概率分布为:

$\begin{matrix} \begin{matrix} q_{k} = \\ \{\begin{matrix} Q_{0} {\bar{p}}^{T} (\overset{k}{\sum_{i = 1}} \frac{P_{V_{1}} A_{i}^{V_{1}} A_{k - i}^{U}}{1 - {\bar{p}}^{T_{V_{1}}}} + \overset{k}{\sum_{i = 1}} \frac{P_{V_{2}} A_{i}^{V_{2}} A_{k - i}^{U}}{1 - {\bar{p}}^{T_{V_{2}}}}, \\ 2 \leq k \leq T_{V 1} \\ Q_{0} {\bar{p}}^{T} (\overset{T_{V_{1}}}{\sum_{i = 1}} \frac{P_{V_{1}} A_{i}^{V_{1}} A_{k - i}^{U}}{1 - {\bar{p}}^{T_{V_{1}}}} + \overset{k}{\sum_{i = 1}} \frac{P_{V_{2}} A_{i}^{V_{2}} A_{k - i}^{U}}{1 - {\bar{p}}^{T_{V_{2}}}}, \\ T_{V_{1}} + 1 \leq k \leq T_{V_{2}} \\ Q_{0} {\bar{p}}^{T} (\overset{T_{V_{1}}}{\sum_{i = 1}} \frac{P_{V_{1}} A_{i}^{V_{1}} A_{k - i}^{U}}{1 - {\bar{p}}^{T_{V_{1}}}} + \overset{T_{V_{2}}}{\sum_{i = 1}} \frac{P_{V_{2}} A_{i}^{V_{2}} A_{k - i}^{U}}{1 - {\bar{p}}^{T_{V_{2}}}}, \\ T_{V_{2}} + 1 \leq k \leq K - 1 \end{matrix} \\ (5) \end{matrix} \end{matrix}$

(3)当k=K时, 忙期开始时刻系统中的数据帧可能在短休假期及之后的启动期到达, 或者在长休假期及之后的启动期到达, 其概率分布为:

$\begin{matrix} \begin{matrix} q_{K} = \\ Q_{0} {\bar{p}}^{T} (\overset{T_{V_{1}}}{\sum_{i = 1}} \frac{P_{V_{1}} A_{i}^{V_{1}} K - i^{U}}{1 - {\bar{p}}^{T_{V_{1}}}} + \overset{T_{V_{2}}}{\sum_{i = 1}} \frac{P_{V 2} A_{i}^{V_{2}} K - i^{U}}{1 - {\bar{p}}^{T_{V_{2}}}}) (6) \end{matrix} \end{matrix}$

一个数据帧传输完成离开后, 系统中的数据帧是由上一个数据帧离去时刻系统中的数据帧与该数据帧的传输时间内到达并进入系统的数据帧构成。所以, 一个数据帧完成传输离去后, 系统中的数据帧数的概率分布为:

$\begin{matrix} Q_{k} = \{\begin{matrix} \overset{k + 1}{\sum_{j = 1}} (q_{j} + Q_{j}) A_{k - j + 1}^{S}, 0 \leq k \leq K - 2 \\ \overset{K - 1}{\sum_{j = 1}} (q_{j} + Q_{j}) K - j^{S} + q_{K}, k = K - 1 \end{matrix} (7) \end{matrix}$

由归一化条件可得:

$\begin{matrix} \overset{K}{\sum_{k = 1}} q_{k} + \overset{K - 1}{\sum_{k = 0}} Q_{k} = 1 (8) \end{matrix}$

综合公式(4)~(8), 采用迭代法, 可求出Q₀的值。

两个连续嵌入点间的平均间隔η 的表达式为:

$\begin{matrix} \begin{matrix} η = Q_{0} \frac{1 - {\bar{p}}^{T}}{p} + Q_{0} {\bar{p}}^{T} (\frac{P_{V_{1}} T_{V_{1}}}{1 - {\bar{p}}^{T_{V_{1}}}} + \frac{P_{V_{2}} T_{V_{2}}}{1 - {\bar{p}}^{T_{V_{2}}}}) + \\ Q_{0} {\bar{p}}^{T} T_{U} + (1 - Q_{0}) b (9) \end{matrix} \end{matrix}$

系统的实际负载ρ ', 即系统利用率为:

$\begin{matrix} ρ' = \frac{(1 - Q_{0}) b}{η} (10) \end{matrix}$

2.3 数据帧的平均等待时间

采用补充变量方法可以求出系统任意时刻数据帧数的概率分布。将系统的状态表示为ξ , ξ =0表示系统处于休假延迟期、短休假期、长休假期或启动期; ξ =1表示系统处于忙期。

休假延迟期D内任意时刻数据帧数的概率分布表达式为:

$\begin{matrix} Q_{0}^{D} \end{matrix}$ =P $\begin{matrix} \{ξ = 0, L = 0\} \end{matrix}$ = $\begin{matrix} \frac{Q_{0} (1 - {\bar{p}}^{T})}{pη} \end{matrix}$ (11)

一个短休假期V₁内任意时刻的数据帧个数L与剩余短休假期 $\begin{matrix} V_{1}^{+} \end{matrix}$ 的联合过程、一个长休假期V₂内任意时刻的数据帧数L与剩余长休假期 $\begin{matrix} V_{2}^{+} \end{matrix}$ 的联合过程、一个启动期U内任意时刻数据帧数L与剩余启动期U⁺的联合过程、一个数据帧传输过程S中任意时刻的数据帧数L与剩余传输时间S⁺的联合过程均可构成马尔可夫链。

短休假期V₁内任意时刻的数据帧数L和剩余短休假期 $\begin{matrix} V_{1}^{+} \end{matrix}$ 的联合概率分布为:

$\begin{matrix} \begin{matrix} Q_{k}^{V_{1}} (y) = \frac{Q_{0} {\bar{p}}^{T} y P_{V_{1}}}{pη (1 - {\bar{p}}^{T_{V_{1}}})} (y^{T_{V_{1}}} {(\frac{p}{y - 1 + p})}^{k + 1} - \\ \overset{k}{\sum_{l = 0}} A_{l}^{V_{1}} {(\frac{p}{y - 1 + p})}^{k - l + 1}) (12) \\ 0 \leq k \leq T_{V_{1}} \end{matrix} \end{matrix}$

长休假期V₂内任意时刻的数据帧数L和剩余长休假期 $\begin{matrix} V_{2}^{+} \end{matrix}$ 的联合概率分布为:

$\begin{matrix} \begin{matrix} Q_{k}^{V_{2}} (y) = \frac{Q_{0} {\bar{p}}^{T} y P_{V_{2}}}{pη (1 - {\bar{p}}^{T_{V_{2}}})} (y^{T_{V_{2}}} {(\frac{p}{y - 1 + p})}^{k + 1} - \\ \overset{k}{\sum_{l = 0}} A_{l}^{V_{2}} {(\frac{p}{y - 1 + p})}^{k - l + 1}) (13) \\ 0 \leq k \leq T_{V_{2}} \end{matrix} \end{matrix}$

逝去的启动期U^-内到达的数据帧数和剩余启动期的联合分布为:

$\begin{matrix} \begin{matrix} σ_{k} (y) = \frac{y}{p T_{U}} (y^{T_{U}} {(\frac{p}{y - 1 + p})}^{k + 1} - \\ \overset{k}{\sum_{i = 0}} A_{i}^{U} {(\frac{p}{y - 1 + p})}^{k - i + 1}) (14) \\ 0 \leq k \leq T_{U} \end{matrix} \end{matrix}$

启动期U内任意时刻的数据帧数L和剩余启动期U⁺的联合概率分布为:

$\begin{matrix} \begin{matrix} Q_{k}^{U} (y) = \overset{\infty}{\sum_{l = 1}} P \{ξ = 0, L = k, U^{+} = l\} y^{l} \\ 1 \leq k \leq K \end{matrix} \end{matrix}$

(1)当1≤ k≤ $\begin{matrix} T_{V_{1}} \end{matrix}$ 时, $\begin{matrix} Q_{k}^{U} \end{matrix} \begin{matrix} (y) \end{matrix}$ 的表达式为:

$\begin{matrix} \begin{matrix} Q_{k}^{U} (y) = \frac{Q_{0} {\bar{p}}^{T} T_{U}}{η} (\overset{k}{\sum_{i = 1}} \frac{P_{V_{1}} A_{i}^{V_{1}} σ_{k - i} (y)}{1 - {\bar{p}}^{T_{V 1}}} + \\ \overset{k}{\sum_{i = 1}} \frac{P_{V_{2}} A_{i}^{V_{2}} σ_{k - i} (y)}{1 - {\bar{p}}^{T_{V_{2}}}}) (15) \end{matrix} \end{matrix}$

(2)当 $\begin{matrix} T_{V_{1}} \end{matrix}$ +1≤ k≤ $\begin{matrix} T_{V_{2}} \end{matrix}$ 时, $\begin{matrix} Q_{k}^{U} \end{matrix} \begin{matrix} (y) \end{matrix}$ 的表达式为:

$\begin{matrix} \begin{matrix} Q_{k}^{U} (y) = \frac{Q_{0} {\bar{p}}^{T} T_{U}}{η} (\overset{T_{V_{1}}}{\sum_{i = 1}} \frac{P_{V_{1}} A_{i}^{V_{1}} σ_{k - i} (y)}{1 - {\bar{p}}^{T_{V_{1}}}} + \\ \overset{k}{\sum_{i = 1}} \frac{P_{V_{2}} A_{i}^{V_{2}} σ_{k - i} (y)}{1 - {\bar{p}}^{T_{V_{2}}}}) (16) \end{matrix} \end{matrix}$

(3)当 $\begin{matrix} T_{V_{2}} \end{matrix}$ +1≤ k≤ K-1时, $\begin{matrix} Q_{k}^{U} \end{matrix} \begin{matrix} (y) \end{matrix}$ 的表达式为:

$\begin{matrix} \begin{matrix} Q_{k}^{U} (y) = \frac{Q_{0} {\bar{p}}^{T} T_{U}}{η} (\overset{T_{V_{1}}}{\sum_{i = 1}} \frac{P_{V_{1}} A_{_{i}}^{V_{1}} σ_{k - i} (y)}{1 - {\bar{p}}^{T_{V_{1}}}} + \\ \overset{T_{V_{2}}}{\sum_{i = 1}} \frac{P_{V_{2}} A_{_{i}}^{V_{2}} σ_{k - i} (y)}{1 - {\bar{p}}^{T_{V_{2}}}}) (17) \end{matrix} \end{matrix}$

(4)当k=K时, $\begin{matrix} Q_{K}^{U} \end{matrix} \begin{matrix} (y) \end{matrix}$ 的表达式为:

$\begin{matrix} \begin{matrix} Q_{K}^{U} (y) = \frac{Q_{0} {\bar{p}}^{T} T_{U}}{η} (\overset{T_{V_{1}}}{\sum_{i = 1}} \frac{P_{V_{1}} A_{_{i}}^{V_{1}} {\bar{σ}}_{K - i} (y)}{1 - {\bar{p}}^{T_{V_{1}}}} + \\ \overset{T_{V_{2}}}{\sum_{i = 1}} \frac{P_{V_{2}} A_{i}^{V_{2}} {\bar{σ}}_{K - i} (y)}{1 - {\bar{p}}^{T_{V_{2}}}}) (18) \end{matrix} \end{matrix}$

式中: $\begin{matrix} {\bar{σ}}_{k} \end{matrix} \begin{matrix} (y) \end{matrix}$ = $\begin{matrix} \overset{\infty}{\sum_{n = k}} \end{matrix}$ σ _k $\begin{matrix} (y) \end{matrix}$ 。

一个数据帧的逝去的传输期S^-内到达的数据帧数和剩余传输期S⁺的联合分布为:

$\begin{matrix} \begin{matrix} ψ_{k} (y) = \frac{y}{pE [S]} (S (y) {(\frac{p}{y - 1 + p})}^{k + 1} - \\ \overset{k}{\sum_{i = 0}} A_{i}^{S} {(\frac{p}{y - 1 + p})}^{k - i + 1}), k \geq 0 (19) \end{matrix} \end{matrix}$

一个数据帧的传输期S内任意时刻的数据帧数L和剩余传输时间S⁺的联合概率分布为:

$\begin{matrix} \begin{matrix} Π_{k}^{*} (y) = \overset{\infty}{\sum_{l = 1}} P \{ξ = 1, L = k, S^{+} = l\} y^{l} \\ 1 \leq k \leq K \end{matrix} \end{matrix}$

(1)当1≤ k≤ K-1时, $\begin{matrix} Π_{k}^{*} \end{matrix} \begin{matrix} (y) \end{matrix}$ 的表达式为:

$\begin{matrix} Π_{k}^{*} (y) = \frac{b}{η} \overset{k}{\sum_{j = 1}} (q_{j} + Q_{j}) ψ_{k - j} (y) (20) \end{matrix}$

(2)当k=K时, $\begin{matrix} Π_{k}^{*} \end{matrix} \begin{matrix} (y) \end{matrix}$ 的表达式为:

$\begin{matrix} Π_{K}^{*} (y) = \frac{b}{η} (\overset{K - 1}{\sum_{j = 1}} (q_{j} + Q_{j}) {\bar{ψ}}_{K - j} (y) + q_{K} {\bar{ψ}}_{K} (y)) (21) \end{matrix}$

式中: $\begin{matrix} {\bar{ψ}}_{k} \end{matrix} \begin{matrix} (y) \end{matrix}$ = $\begin{matrix} \overset{\infty}{\sum_{n = k}} \end{matrix}$ ψ _k $\begin{matrix} (y) \end{matrix}$ 。

结合公式(11)~(13), 得系统中任意时刻的数据帧数L=0的概率分布为:

$\begin{matrix} P \{L = 0\} = Q_{0}^{D} (1) + Q_{0}^{V_{1}} (1) + Q_{0}^{V_{2}} (1) = \frac{Q_{0}}{pη} (22) \end{matrix}$

结合公式(12)(13)(15)(20), 得系统中任意时刻的数据帧数L=k $\begin{matrix} (1 \leq k \leq T_{V_{1}}) \end{matrix}$ 的概率分布为:

$\begin{matrix} P \{L = k\} = \frac{Q_{k}}{pη} (23) \end{matrix}$

结合公式(13)(16)(20), 得系统中任意时刻的数据帧数L=k $\begin{matrix} (T_{V_{1}} + 1 \leq k \leq T_{V_{2}}) \end{matrix}$ 的概率分布为:

$\begin{matrix} P \{L = k\} = Q_{k}^{V_{2}} (1) + Q_{k}^{U} (1) + Π_{k}^{*} (1) = \frac{Q_{k}}{pη} (24) \end{matrix}$

结合公式(17)(20), 得系统中任意时刻的数据帧数L=k $\begin{matrix} (T_{V_{2}} + 1 \leq k \leq K - 1) \end{matrix}$ 的概率分布为:

$\begin{matrix} P \{L = k\} = Q_{k}^{U} (1) + Π_{k}^{*} (1) = \frac{Q_{k}}{pη} (25) \end{matrix}$

综合公式(22)~(25), 系统中任意时刻的数据帧数L=k $\begin{matrix} (0 \leq k \leq K - 1) \end{matrix}$ 的概率分布为:

$\begin{matrix} P \{L = k\} = \frac{Q_{k}}{pη} (26) \end{matrix}$

此外, 结合公式(18)(21), 得系统中任意时刻的数据帧数L=K的概率分布为:

$\begin{matrix} P \{L = K\} = Q_{K}^{U} (1) + Π_{K}^{*} (1) = 1 - \frac{ρ'}{ρ} (27) \end{matrix}$

式中:ρ =pb为系统的输入负载。

结合公式(26)(27), 可得系统的平均队长为:

$\begin{matrix} E [L] = \frac{1}{pη} \overset{K - 1}{\sum_{k = 1}} k Q_{k} + K (1 - \frac{ρ'}{ρ}) (28) \end{matrix}$

在FCFS系统中, 由Little公式^[14]可得数据帧的平均等待时间为:

E $\begin{matrix} [W] \end{matrix}$ = $\begin{matrix} \frac{b}{pρ' η} \end{matrix} \begin{matrix} \overset{K - 1}{\sum_{k = 1}} \end{matrix}$ kQ_k+ $\begin{matrix} \frac{K}{p} \end{matrix} \begin{matrix} (\frac{ρ}{ρ'} - 1) \end{matrix}$ -b (29)

3 性能指标

系统阻塞率P_B是指新到达的数据帧因系统缓存满而被系统阻塞的概率, 即数据帧到达时刻系统中的数据帧数为K的概率。P_B表达式为:

$\begin{matrix} P_{B} = pP \{L = K\} = p (1 - \frac{ρ'}{ρ}) \end{matrix}$

能量节省率α 定义为稳态下系统处在休眠状态的概率。当休眠延迟期内无数据帧到达时, 系统的忙循环内将有一个休眠阶段, 则α 的表达式为:

$\begin{matrix} α = \frac{Q_{0} {\bar{p}}^{T} E [T_{V}]}{η} \end{matrix}$

数据帧延迟σ 指从数据帧到达系统的时刻开始, 到数据帧传输完毕离开系统时刻的这段间隔。该指标对应于排队模型中数据帧的逗留时间。数据帧延迟σ 的表达式为:

$\begin{matrix} σ = E [W] + b = \frac{b}{pρ' η} \overset{K - 1}{\sum_{k = 1}} k Q_{k} + \frac{K}{p} (\frac{ρ}{ρ'} - 1) \end{matrix}$

4 数值实验与仿真实验

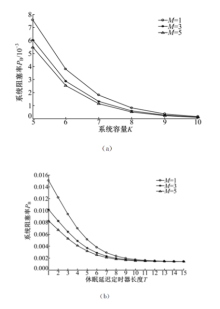
根据文献[15]进行数值实验时的参数设置, 本文的系统参数设定如下:1 slot=1 ms, 一个数据帧的平均传输时间b=2 ms, 输入负载ρ =0.8, 启动期的长度T_U=6 ms, 短休假期的长度 $\begin{matrix} T_{V_{1}} \end{matrix}$ =1 ms, 长休假期的长度 $\begin{matrix} T_{V_{2}} \end{matrix}$ =5 ms。

不同短休眠窗口数量阈值下, 系统阻塞率随系统容量和休眠延迟期长度的变化趋势如图1所示。

	Figure Option View Download New Window
	图1 系统阻塞率的变化趋势Fig.1 Change trend of system block ratio

由图1可知, 对于确定的系统容量, 或者休眠延迟定时器长度, 随着短休眠窗口数量阈值的增大, 系统阻塞率呈下降趋势。短休眠窗口数量阈值越大, 表示系统中短休眠窗口数量越多, 数据帧在短休眠阶段到达的概率相应增大。由于在短休眠阶段到达的数据帧被阻塞的概率较小, 所以系统阻塞率降低。从图1(a)可以看出, 随着系统容量的增大, 系统阻塞率呈下降趋势。这是因为系统容量越大, 系统缓冲区中可以容纳的数据帧越多, 数据帧被阻塞的概率也就变小。从图1(b)还可以看出, 随着休眠延迟定时器长度的增大, 系统阻塞率也呈下降趋势。这是因为休眠延迟定时器的长度越大, 数据帧在休眠延迟阶段到达的概率就越大, 由于在休眠延迟期内到达的数据帧将使系统立即返回到工作状态并进行数据帧传输, 不会造成系统缓存中数据帧数量增多, 从而降低数据帧被阻塞的概率, 系统阻塞率变小。

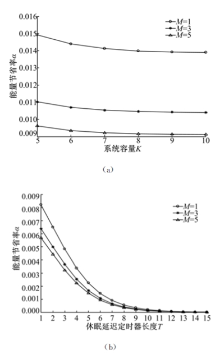
不同短休眠窗口数量阈值下, 能量节省率随系统容量和休眠延迟期长度的变化趋势如图2所示。

	Figure Option View Download New Window
	图2 能量节省率的变化趋势Fig.2 Change trend of energy saving ratio

由图2可知, 对于一个确定的系统容量, 或者休眠延迟定时器长度, 随着短休眠窗口数量阈值的变大, 能量节省率呈下降趋势。短休眠窗口数量阈值越大, 表示系统中短休眠窗口的数量越多, 数据帧在短休眠阶段到达的概率增大。由于系统在短休眠阶段比在长休眠阶段节省的能量少, 所以能量节省率降低。从图2(a)可以看出, 系统容量越大, 能量节省率越小。这是因为系统容量越大, 单位时间内到达并进入系统的数据帧越多, 从而增加系统的工作时间, 系统处在休眠阶段的时间减少, 能量节省率也就变小。从图2(b)还可以看出, 随着休眠延迟定时器长度的增大, 能量节省率呈下降趋势。这是因为休眠延迟定时器越大, 数据帧在休眠延迟阶段到达的概率就越大。由于在休眠延迟阶段到达的数据帧立即被传输, 使得系统进入休眠阶段的概率较小, 能量节省率也随之降低。

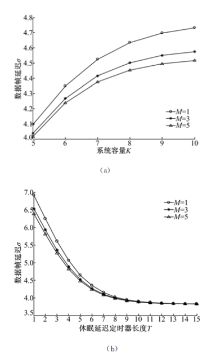
不同短休眠窗口数量阈值下, 数据帧延迟随系统容量和休眠延迟期长度的变化趋势如图3所示。

从图3可以看出, 对于确定的系统容量或者休眠延迟定时器长度, 随着短休眠窗口数量阈值变大, 数据帧延迟呈下降趋势。短休眠窗口数量阈值越大, 表示系统中的短休眠窗口数量越多, 数据帧在短休眠阶段到达的概率就越大。由于短休眠阶段内到达的数据帧的等待时间较短, 所以数据帧延迟相对较小。由图3(a)可知, 随着系统容量的增大, 数据帧延迟也增大。这是因为系统容量越大, 系统缓冲区中可以容纳更多的数据帧数, 新到达数据帧的等待时间越长, 数据帧延迟也就越大。由图3(b)可知, 随着休眠延迟定时器长度的增大, 数据帧延迟呈下降趋势。这是因为休眠延迟定时器长度越大, 数据帧在休眠延迟阶段到达的概率就越大, 由于在休眠延迟阶段到达的数据帧可以立即被传输, 因此数据帧延迟变小。

沿用理论分析数值实验中的系统参数, 以M=5为例, 针对不同的休眠延迟定时器长度T和系统容量K, 进行200 000次系统仿真。基于理论分析和系统仿真的对比实验结果见表1。

由表1可知, 系统性能指标的理论分析结果与仿真统计结果是吻合的, 这进一步说明了系统模型建立的合理性及理论推导过程的正确性。

	Figure Option View Download New Window
	图3 数据帧延迟的变化趋势Fig.3 Change trend of average latency of data frames

表1 理论结果与仿真结果的比较 Table 1 Comparison of analysis results and simulation results

综合上述的实验结果可以看出, 较大的系统容量在降低系统阻塞率的同时, 也会削弱系统的能量节省效果, 并加大数据帧延迟; 较大的休眠延迟定时器长度在降低系统阻塞率及数据帧延迟的同时, 又会降低系统的节能效果。因此, 在设置系统容量及休眠延迟定时器长度时, 需折衷考虑多种性能指标。为此, 综合系统阻塞率, 能量节省率和数据帧延迟, 构造成本函数如下:

F $\begin{matrix} (X) \end{matrix}$ =C₁P_B+C₂σ +C₃/α

式中:C₁, C₂和C₃分别为系统阻塞率, 数据帧延迟和能量节省率对系统成本的影响因子。当X分别为系统容量K和休眠延迟定时器长度T时, 可以得到成本函数F(K)和成本函数F(T)。

针对不同的阈值, 成本函数随系统容量和休眠延迟期长度的变化趋势如图4所示。

	Figure Option View Download New Window
	图4 成本函数的变化趋势Fig.4 Change trend of cost function

由图4可知, 当短休眠窗口数量阈值一定时, 随着系统容量或休眠延迟定时器长度的增大, 成本函数首先呈下降趋势, 当系统容量或休眠延迟定时器长度进一步增大时, 成本函数又呈上升趋势。由此可见, 分别存在一个最优的系统容量和休眠延迟定时器长度, 使成本函数达到最低值。

本实验中, 不同的短休眠窗口数量阈值下, 最优的系统容量K^*和休眠延迟定时器长度T^*及其对应的成本函数的最小值F(K^*)和F(T^*)如表2所示。

表2 系统参数的优化 Table 2 Optimization of system parameters

5 结束语

本文提出了一种带有休眠延迟机制的DRX节能策略, 并建立了一个带有休眠延迟和启动阶段的多重休假排队模型。综合使用嵌入Markov链方法和补充变量方法, 考虑有限容量, 对排队模型进行了稳态分析, 导出了系统阻塞率、能量节省率和数据帧延迟等系统性能指标的表达式。分别基于理论分析和改进的DRX节能策略的工作机制对排队模型进行了数值实验和系统仿真, 结果表明, 本文所提出的带有休眠延迟机制的DRX节能策略降低了系统阻塞率和能量消耗, 并改善了系统的响应性能。同时, 实验结果还揭示出, 在设置系统容量和休眠延迟定时器时, 不同的性能指标之间存在折衷关系。通过构造成本函数, 进行了节能策略的系统优化。本文的研究成果为无线网络通信中DRX节能策略的进一步改进奠定了理论基础。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Jailani E, Ibrahim M, Rahman R A. LTE speech traffic estimation for network dimensioning[C]∥Symposium on Wireless Technology and Applications, 2012: 315-320. [本文引用:1]
[2]	Cao J, Ma M, Li H, et al. A survey on security aspects for LTE and LTE-A networks[J]. IEEE Communications Surveys & Tutorials, 2013, 16(1): 1-20. [本文引用:1]
[3]	Abeta S. Toward LTE commercial launch and future plan for LTE enhancements (LTE-Advanced)[C]∥International Conference of Communication System (ICCS): 146-150. [本文引用:1]
[4]	Shin S C, Lee Y P. Testing of early applied LTE-Advanced technologies on current LTE service to overcome real network problem and to increase data capacity[C]∥15th International Conference on Advanced Communication Technology, 2013: 275-281. [本文引用:1]
[5]	林闯, 田源, 姚敏. 绿色网络和绿色评价: 节能机制、模型和评价[J]. 计算机学报, 2011, 34(4): 593-612. Lin Chuang, Tian Yuan, Yao Min. Green network and green evaluation: energy saving mechanism, model and evaluation[J]. Chinese Journal of Computers, 2011, 34(4): 593-612. [本文引用:1]
[6]	Ciochina C, Mottier D, Sari H. An analysis of three multiple access techniques for the uplink of future cellular mobile systems[J]. European Transactions on Telecommunications, 2008, 19(5): 581-588. [本文引用:1]
[7]	Zhang Y, Gao S, Tian H, et al. Delay analysis of DRX in LTE-advanced considering carrier aggregation[J]. Journal of China Universities of Posts and Telecommunications, 2011, 18(6): 1-7. [本文引用:1]
[8]	Ting K C, Wang H C, Tseng C C, et al. Energy-efficient DRX scheduling for QoS traffic in LTE networks[C]∥9th International Symposium on Parallel and Distributed Processing with Applications, 2011: 213-218. [本文引用:1]
[9]	Yin F. An application aware discontinuous reception mechanism in LTE-advanced with carrier aggregation consideration[J]. Annales Des Telecommunications-Annals of Telecommunications, 2012, 67(3/4): 147-159. [本文引用:1]
[10]	Mihov Y Y, Kassev K M, Tsankov B P. Analysis and performance evaluation of the DRX mechanism for power saving in LTE[C]∥26th Convention of Electrical and Electronics Engineering in Israel, 2010: 520-524. [本文引用:1]
[11]	麦岳波, 林晓辉. LTE无线系统终端省电机制研究[J]. 计算机工程, 2011, 37(15): 279-282. Mai Yue-bo, Lin Xiao-hui. Research on terminal electricity saving mechanism of LTE wireless system[J]. Computer Engineering, 2011, 37(15): 279-282. [本文引用:1]
[12]	Wen Y, Liang J, Niu K, et al. Performance analysis and optimization of DRX mechanism in LTE[C]∥International Conference on Network Infrastructure and Digital Content, 2012: 71-75. [本文引用:1]
[13]	Wang H C, Tseng C C, Chen G Y, et al. Accurate analysis of delay and power consumption of LTE DRX mechanism with a combination of short and long cycles[C]∥15th International Symposium onWireless Personal Multimedia Communications, 2012: 384-388. [本文引用:1]
[14]	田乃硕, 徐秀丽, 马占友. 离散时间排队论[M]. 北京: 科学出版社, 2008. [本文引用:1]
[15]	Jin S, Yue W. System modeling and performance analysis of the power saving class type II in BWA networks[J]. Journal of Global Optimization, 2013, 56(4): 1375-1391. [本文引用:1]

2012

0.0

... 然而,目前的网络应用日益暴露出能耗高、效率低、浪费多等诸多问题^[1,2] ...

2013

0.0

... 然而,目前的网络应用日益暴露出能耗高、效率低、浪费多等诸多问题^[1,2] ...

0.0

... 长期演进技术LTE(Long term evolution)作为第三代合作伙伴计划3GPP(the 3rd generation partner project)标准,从通用移动通信系统UMTS(Universal mobile telecommunications system)技术衍生而来,也称为4G标准^[3,4] ...

2013

0.0

2011

0.0

. 2011, 34(4):593-612 DOI:doi:10.3724/SP.J.1016.2011.00593

Green network and green evaluation: energy saving mechanism, model and evaluation

绿色网络和绿色评价:节能机制、模型和评价

Lin Chuang , Tian Yuan , Yao Min.

林闯, 田源, 姚敏

随着网络规模的扩大和网络设备的不断更新,目前的网络对能量的利用日益暴露出能耗高、效率低,浪费多等诸多问题.节省网络能耗、构建绿色网络不仅成为计算机领域一个意义重大、需要迫切解决的课题,也成为影响社会可持续发展和国家发展战略的一个重要因素.目前,大量绿色网络的研究工作致力于减少网络系统的无用能耗,提高能量利用率.文中将能量看成一种系统资源,从资源分配和任务管理角度对绿色网络的机制和策略进行了综述,介绍了模型方法在绿色评价中的应用.基于这些讨论,文中提出了基于随机模型的绿色评价框架,为构建绿色网络和节能机制的评价体系奠定了基础.

... 同时,LTE引入了一种非连续接收DRX(Discontinuous reception)省电工作机制^[5] ...

2008

0.0

2011

0.0

2011

0.0

2012

0.0

... 1 DRX节能策略及系统模型LTE中的DRX节能策略,定义在媒体访问控制MAC(Media access control)子层,按照工作状态分为空闲状态DRX(IDLE DRX)和连接状态DRX(ACTIVE DRX)^[9,10,11] ...

2010

0.0

2011

0.0

. 2011, 37(15):279-282 DOI:doi:10.3969/j.issn.1000-3428.2011.15.091

Research on terminal electricity saving mechanism of LTE wireless system

LTE无线系统终端省电机制研究

Mai Yue-bo , Lin Xiao-hui.

麦岳波, 林晓辉

Aiming at the demerits of the lower business and higher power consumption, etc., in constant power dormancy mode of the Long Term Evolution(LTE) system. This paper proposes a variation of power dormancy algorithm at first, which can dynamically change the dormancy period according to the demands of terminal business, promote the standby time of terminal, then, discusses several problems about the average response time and average consumption of the terminal in the dormant state under this algorithm. Simulation experiments show that, compared with constant power dormancy algorithm, the energy consumption can be reduced by 6%~12% in this algorithm.

针对长期演进(LTE)系统恒功率休眠模式中存在的低业务、高功耗等缺点，提出一种变功率休眠算法。该算法可根据终端业务要求，动态改变休眠周期，以提高终端的待机时间，并以该算法为基础，探讨休眠状态终端的平均响应时间和平均功耗等问题。仿真实验表明，与恒功率休眠算法相比，该变功率休眠算法可以减少功耗6%~12%。

2012

0.0

... 如果有数据帧到达,UE发送一个无线资源控制协议RRC(Radio resource control)请求,与基站eNB(Evolved nodeB)重新建立一个空口连接^[12],启动监听PDCCH ...

2012

0.0

... 当有数据帧到达时,由于系统在这个状态下依然存在RRC连接,UE不需要和eNB重新建立空口连接,便可启动监听PDCCH,迅速转到工作状态,因此可以减少信令开销,加快传输速度^[13] ...

2008

0.0

... 在FCFS系统中,由Little公式^[14]可得数据帧的平均等待时间为: ...

2013

0.0