基于自适应和小波模极大值重构的地面核磁共振信号噪声压制方法

引用本文

孙淑琴, 孟庆云, 方秀成, 林君, 王应吉, 田宝凤, 杨楠. 基于自适应和小波模极大值重构的地面核磁共振信号噪声压制方法. 2015, 45(5): 1642-1651
SUN Shu-qin, MENG Qing-yun, FANG Xiu-cheng, LIN Jun, WANG Ying-ji, TIAN Bao-feng, YANG Nan. Noise cancellation algorithm for surface magnetic resonance signals based on. Journal of Jilin University Engineering and Technology Edition, 2015, 45(5): 1642-1651 复制到剪切板

Permissions

基于自适应和小波模极大值重构的地面核磁共振信号噪声压制方法

孙淑琴¹, 孟庆云¹, 方秀成¹, 林君¹, 王应吉¹, 田宝凤¹, 杨楠¹

1.吉林大学仪器科学与电气工程学院,长春 130061

林君(1954-),男,教授,博士生导师.研究方向:地球物理探测技术,仪器和虚拟仪器.E-mail:lin_jun@jlu.edu.cn

作者简介:孙淑琴(1969-),女,教授.研究方向:核磁共振理论与应用.E-mail:sunsq@jlu.edu.cn

基金:国家重大科学仪器设备开发专项项目(2011YQ030133)

摘要

针对核磁共振信号中的噪声,在二进小波变换基本原理的基础上,研究了小波模极大值重构方法,将该方法与自适应滤波方法相结合应用到含噪声信号的干扰滤除中,通过分析包络信号拟合后的初始振幅、平均衰减时间和相位等数据可知,含噪声信号经自适应和小波模极大值重构方法滤波处理后拟合得到的特征参数误差最小且信噪比得到最大的提高。同时,通过实测数据得知采用自适应和小波模极大值重构方法进行噪声滤波后的结果与钻孔结果的一致性较好,验证了本文所提方法的有效性。

关键词: 通信技术; 核磁共振; 干扰滤除; 自适应滤波; 小波模极大值重构滤波

中图分类号:TN911 文献标志码:A 文章编号:1671-5497(2015)05-1642-10

Noise cancellation algorithm for surface magnetic resonance signals based on

SUN Shu-qin¹, MENG Qing-yun¹, FANG Xiu-cheng¹, LIN Jun¹, WANG Ying-ji¹, TIAN Bao-feng¹, YANG Nan¹

1.College of Instrumentation and Electrical Engineering, Jilin University, Changchun 130061, China

Abstract

Based on the principle of binary wavelet transform, a method of reconstruction of wavelet modulus maximum value for the noise in Magnetic Resonance Sound (MRS) signals is proposed. Combined with adaptive notch filter, the method is used to filter out noise. By analysis of the data of the initial amplitude, the average decay time and phase etc posterior the fitting of envelope signals, it is known that after several times of filtering processing of the noise signals, the obtained fitting error of the characteristic parameters is minimum, and the Signal to Noise Ratio (SNR) is obviously improved. Real data were measured and noise filtering was carried out using the proposed method in this paper. The obtained results are in good agreement with the drilling results, which verifies the effectiveness of the proposed method.

Keyword: communication technology; magnetic resonance sounding; interference filter; adaptive filter; reconstruction of wavelet modulus maximum value

Show Figures

0 引言

核磁共振测水方法是利用地层中丰度最高的氢原子核的顺磁性产生的核磁共振(Magnetic resonance sounding, MRS)信号, 通过改变激发电流的大小完成对不同深度地下水的测量^{[1, 2]}。对采集的信号经过滤波处理之后, 即可反演解释得到地下含水层深度、厚度、含水量大小、含水层平均孔隙度等信息^{[3, 4]}。

国内外专家学者提出了多种方法来抑制噪声, 主要有:仪器采集数据的叠加方法^{[5, 6]}, 缺点在于叠加次数多, 系统的工作效率低; 探测线圈采用八字形线圈^{[7, 8]}方式, 与圆形探测线圈相比, 探测深度降低一半; 采用同步检波和FIR低通滤波技术^{[9, 10]}的方法会引起有用信号的失真; 此外还有滑动平均滤波法、区块对消法, 正弦对消法、陷波滤波器法^{[11, 12, 13, 14, 15, 16, 17, 18]}。这几种方法主要针对电磁噪声的滤除, 由于噪声的无规律性, 以上滤波方法均存在一定的局限性。

上述滤波方法主要针对MRS信号中振幅提取的效果进行分析和处理, 然而未对MRS信号中频率、平均衰减时间、相位等其他几个特征参数提取情况进行分析和总结。本文研究了自适应和小波模极大值重构方法, 自适应滤波方式主要是针对固定频率噪声的滤波处理, 小波模极大值重构方法主要是针对白噪声的滤波处理^{[19, 20, 21, 22]}。将两者结合起来能够突破传统傅里叶变换在时域没有任何分辨率的限制, 具有良好的时域分析特性, 能够从强干扰的信号中提取有用成分, 弥补了其他方法在非平稳信号处理上的不足。将本文方法与自适应滤波方法和小波模极大值重构方法进行了对比, 可知用本文方法所得到的信噪比更高, 信号曲线与噪声曲线能够得到明显的分开, 且信号和噪声的曲线都变得更光滑, 对水文地质参数的解释更准确。

1 核磁共振测试信号及数据处理

1.1 数据处理流程

利用JLMRS仪器所采集的信号中通常混有复杂的噪声成分, 表达式如下:

$\begin{matrix} \begin{matrix} E (t) = \cos (2 π f_{0} t + φ_{0}) \sum_{n} E_{n} e^{- α_{n} t} + \\ \sum_{m} U_{m} \cos (2 π f_{m} t + φ_{m}) + ε_{real} (t) (1) \end{matrix} \end{matrix}$

式中:第一项为MRS信号表达式; 第二项为工频谐波噪声表达式, 由多个单频的谐波分量叠加而成, 其中每个单频率谐波的参数都是独立的; 第三项为随机噪声, ε _real(t)中包含平稳的随机噪声和非平稳的随机噪声。

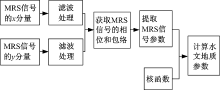
仪器测试信号的数据处理过程如图1所示。测试信号经过正交分解、噪声滤除、提取信号的初始振幅E₀, 平均衰减时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ , 接收频率f和初始相位φ ₀后, 经过反演计算即可得到地下含水量及含水层孔隙度等信息。MRS数据参数为E₀、 $\begin{matrix} T_{2}^{*} \end{matrix}$ 、φ ₀, 相应的水文地质参数为单位体积含水量(有效孔隙度)、空隙大小(渗透性)和含水层导电性(电阻率)。MRS信号的几个特征参数对于含水地层的解释均有直接关系。

	Figure Option View Download New Window
	图1 MRS信号数据处理流程图Fig.1 Flowchart of MRS signal data processing

1.2 自适应滤波算法原理

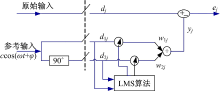
当原始信号中包含频率为ω 的工频谐波干扰时, 利用自适应滤波器可以消除这种特定频率成分的干扰, 自适应滤波器结构图^[23]如图2所示。图中核磁共振信号与干扰信号叠加, 经采样后给d_j端, 参考输入是与单频干扰相关的正弦信号, 采样送到d₁_j、d₂_j端, d₂_j是由参考信号经过90° 相移得来, 由两个参考信号得到ω ₁_j、ω ₂_j两个权值, 即自由度, 使得组合后正弦波振幅、相角与原始输入干扰分量的振幅、相角相同, 从而使输出的e_j中的ω 被抵消掉, 达到滤波的目的。

	Figure Option View Download New Window
	图2 自适应滤波器结构图Fig.2 Structure chart of adaptive trap

1.3 二进小波变换

设信号f(t)是平方可积的, 即f(t)∈ L²(R), 则这一信号的二进小波变换定义为^[24]:

$\begin{matrix} W_{f} (2^{j}, τ) = \frac{1}{\sqrt[]{2^{j}}} \int_{-}^{\infty} f (t) ψ^{*} (\frac{t - τ}{2^{j}}) dt (2) \end{matrix}$

式中:j∈ z; τ 为平移参数; ψ (t)为母小波。

假设χ (t)为尺度函数, 应用式(2)可知χ (t)、ψ (t)满足以下尺度方程:

$\begin{matrix} \begin{matrix} χ (t) = \sqrt[]{2} \overset{\infty}{\sum_{k = - \infty}} α (k) χ (2 t - k) (3) \\ ψ (t) = \sqrt[]{2} \overset{\infty}{\sum_{k = - \infty}} β (k) χ (2 t - k) (4) \end{matrix} \end{matrix}$

式中:α 为低通滤波器:β 为高通滤波器。

如果对式(2)的τ 进行离散化, 并假设χ (t)∈ L²(R)、ψ (t)∈ L²(R), 二进小波变换的小波系数和尺度系数为:

$\begin{matrix} \begin{matrix} d_{j} (k) = \frac{1}{\sqrt[]{2^{j}}} \int_{-}^{\infty} f (t) ψ (\frac{t - k}{2^{j}}) dt = f * {\overset{__}{ψ}}_{2^{j}} (k) (5) \\ s_{j} (k) = \frac{1}{\sqrt[]{2^{j}}} \int_{-}^{\infty} f (t) χ (\frac{t - k}{2^{j}}) dt = f * {\overset{__}{χ}}_{2^{j}} (k) (6) \end{matrix} \end{matrix}$

式中:k∈ z; $\begin{matrix} {\overset{__}{χ}}_{2^{j}} \end{matrix}$ (t)= $\begin{matrix} χ_{2^{j}} \end{matrix}$ (-t)= $\begin{matrix} \frac{1}{\sqrt[]{2^{j}}} \end{matrix}$ χ (- $\begin{matrix} \frac{t}{2^{j}} \end{matrix}$ ); $\begin{matrix} {\bar{ψ}}_{2^{j}} \end{matrix}$ = $\begin{matrix} ψ_{2^{j}} \end{matrix}$ (-t)= $\begin{matrix} \frac{1}{\sqrt[]{2^{j}}} \end{matrix}$ ψ (- $\begin{matrix} \frac{t}{2^{j}} \end{matrix}$ ); * 为卷积运算。

经过滤波器级联结构求出各尺度上的小波系数。令α _j(k)和β _j(k)分别是在滤波器α (k)和β (k)每两个系数之间添加2^j-1个零后所得到的滤波器, 记 $\begin{matrix} {\overset{__}{α}}_{j} \end{matrix}$ (k)=α _j(-k), $\begin{matrix} \overset{__}{β_{j}} \end{matrix}$ (k)=β _j(-k)。二进小波变换的快速分解算法为:

$\begin{matrix} \begin{matrix} s_{j + 1} (k) = s_{j} * {\overset{__}{α}}_{j} (k) (7) \\ d_{j + 1} (k) = s_{j} * \overset{__}{β_{j}} (k) (8) \end{matrix} \end{matrix}$

快速重构算法为:

$\begin{matrix} s_{j} (k) = \frac{1}{2} [s_{j + 1} * α_{j} (k) + d_{j + 1} * β_{j} (k)] (9) \end{matrix}$

1.4 小波模极大值重构消噪的原理

将含有噪声的信号进行多尺度小波分解, 求取相应的模极大值, 然后根据信号和噪声在不同尺度因子下的不同传播特性来区分信号和噪声, 这就是小波模极大值重构消噪的理论依据。

通过Lipschitz指数α 可以度量信号在某个时间区间或某一时刻的正规性, 即刻画信号的奇异性。奇异性也可以通过跟踪小波变换在细尺度下的模极大值来检测。而且Lipschitz指数和二进小波变换模极大值之间存在以下关系:如果信号的Lipschitz指数α > 0, 该信号的二进小波变换模极大值将随着尺度的增大而增大, 这样模极大值点是由需要的信号所产生; 反之, α < 0, 该信号的二进小波变换模极大值将随着尺度的增大而减小, 这样的模极大值由噪声产生。

根据以上原理可知, 随着尺度因子的不断变大, 噪声小波系数的模极大值点的幅度值将明显变小。经过几次二进小波变换之后, 由噪声产生的模极大值点的幅度值已经变得非常小, 甚至很多由噪声产生的模极大值点的值都变为零, 这样剩下的模极大值点主要是由信号产生的。一般情况下, 尺度越大, 信号产生的小波系数模极大值点的比例就越大, 大分解尺度上的模极大值点主要是由信号产生的。所以就可以利用大尺度上的小波系数模极大值点逐步确定由信号产生的小尺度上的小波系数模极大值点, 最后根据剩余的模极大值点重构信号, 这样就能够将噪声削弱。

1.5 小波模极大值重构消噪过程

根据小波模极大值重构消噪原理, 消噪算法过程如下:

(1)对含有噪声的信号进行二进小波变换, 小波分解尺度的总个数选择应该适中, 一般小波分解尺度数为4或5, 大于此值有用信号可能会丢失, 小于此值不能保证产生的小波系数模极大值点的优势程度。最后, 求出小波系数的模极大值点及相对应的模极大值。

(2)设定小波系数的阈值为T, 最大尺度上的小波系数模极大值如果大于阈值T, 则保留相对应的小波模极大值点, 否则剔除相对应的小波模极大值点, 从而使最大尺度上小波系数的小波模极大值点更新。根据核磁共振实际处理, 假设阈值T=0.1max, 其中max表示小波模极大值中的最大值。

(3)假设最大尺度为j。利用第(2)步中的小波模极大值点的位置构造U(x_jn), x_jn为尺度j上的第n个小波模极大值点, 之后在U(x_jn)内找到尺度j-1上的小波系数模极大值点, 使尺度j-1上位于U(x_jn)内的模极大值点保留, 其余的小波模极大值点进行清除, 尺度j-1上的小波模极大值点就进行了更新。假设j=j-1, 当尺度数为2时, 停止循环第(3)步。

(4)尺度j=1或j=2位置上相对应的极大值点进行保留, 其他位置的极大值点置为零。

(5)应用各个尺度上余下的小波模极大值点进行小波系数的重构, 最后利用重构的小波系数重构信号。

2 仿真模型的建立

在地下水探测技术中, 核磁共振仪器采用4倍频采样的数字正交技术来获得包络信号。模拟这样的一个理想信号并加入干扰噪声来验证本文研究方法的效果, 将处理后的信号与原始信号作对比, 以信噪比(信号强度与噪声强度的比值)高低为评价指标, 验证本文方法的可行性效果。

定义信号的信噪比如下:

$\begin{matrix} SNR = \sqrt[]{\frac{\overset{M}{\sum_{n = 1}} (S_{x}^{2} (n) + S_{y}^{2} (n))}{\overset{M}{\sum_{n = 1}} (N_{x}^{2} (n) + N_{y}^{2} (n))}} (10) \end{matrix}$

式中:S_x、S_y分别为含噪信号的x分量和y分量; N_x、N_y分别为噪声的x分量和y分量。

2.1 理想信号仿真

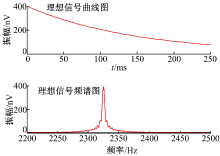
核磁共振信号中的噪声主要是白噪声和工频噪声, 工频噪声频率一般为50 Hz的整数倍, 为了模拟野外的实际信号, 在理想信号中叠加白噪声和工频噪声。建立仿真模型, 信号初始振幅E₀设为400 nV, 初始相位φ ₀设为165° , 弛豫时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ 设为150 ms, 频率f设为2325 Hz的理想衰减正弦波信号, 其包络信号和频谱图如图3所示。

	Figure Option View Download New Window
	图3 理想包络信号和频谱图Fig.3 Ideal signal envelope and spectrum diagram

2.2 信号加入白噪声

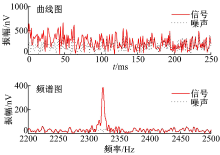
首先在包络信号上加入高斯白噪声, 其幅值为150 nV。此时信号的信噪比为1.43, 见图4。

	Figure Option View Download New Window
	图4 白噪声包络信号和频谱图Fig.4 Signal envelope and spectrum diagram of white noise

	Figure Option View Download New Window
	图5 去噪前后模极大值点对比Fig.5 Contrast before and after of modulus maxima

对加入白噪声的MRS信号与经小波模极大值重构处理后的MRS信号进行模极大值点的对比如图5所示。由图可知:原始数据中噪声大部分集中于第1层和第2层, 经小波模极大值重构处理后保存下来的系数较少。随着分解尺度的增加噪声部分越来越少, 有用信号成为主要部分, 所以保留下来的系数也越来越多。小波模极大值重构算法的主要优点是根据小波变换系数模极大值的跨尺度传播规律, 可以明确区分每一分解层次上代表噪声和信号的小波变换系数, 既不会去掉微弱的有用信号, 也不会保留强度较大的噪声^[25]。

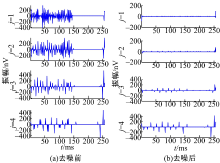
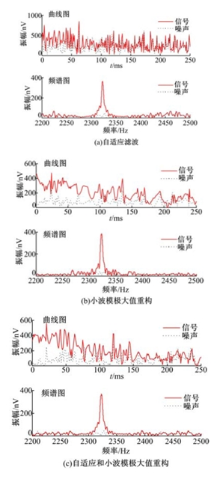
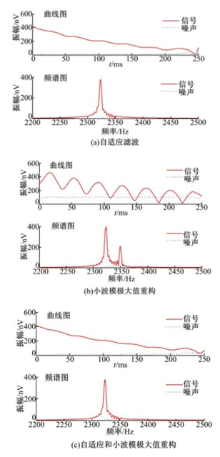
自适应滤波主要针对固定频率噪声的滤除, 小波模极大值重构主要针对白噪声的滤除, 为了反映基于自适应和小波模极大值重构滤波方法的优越性, 下面给出了几种滤波方式的对比。经过不同滤波方式所得到的包络信号和频谱图如图6所示。图6(b)和(c)所得到的曲线变得比较光滑, 信号与噪声明显地被分开。在3种滤波方法中, 经自适应和小波模极大值重构所得到的信噪比最高, 所以经此种滤波方式所得到的信号是最可信的。

	Figure Option View Download New Window
	图6 处理之后的包络信号和频谱图Fig.6 Envelope signal and the spectrum diagram after filtering

对加入白噪声的信号进行滤波, 比较滤波前后情况, 白噪声在整个频域范围内均匀分布, 无固定频率值。比较结果如表1所示。

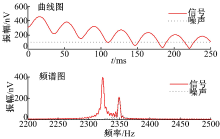
由表1可以看出:经过自适应和小波模极大值重构处理的数据与另外两种方法对比, 所得到的特征参数最接近于理想信号且信噪比最高, 信噪比可达到2.61。经过自适应和小波模极大值重构处理后的MRS特征参数的拟合误差E₀%达到0.82%, $\begin{matrix} T_{2}^{*} \end{matrix}$ 达到6.3%, φ ₀%达到1.75%, 频谱幅度衰减率达到0.12%, 满足实际应用的要求^{[14, 15]}。MRS数据处理之后, 所得到的特征参数越接近于理想信号说明处理的结果越准确, 反演解释结果的可信度越高。同时由图6可得, 经自适应滤波和小波模极大值重构方法所得到的信号曲线和噪声曲线变得比较光滑且信号与噪声明显分开, 获得了可信的包络信号。

2.3 信号加入工频噪声

理想信号中加入工频谐波干扰, 其中频率f₁=2350 Hz, 幅值为80 nV。信噪比为2.88, 如图7所示。

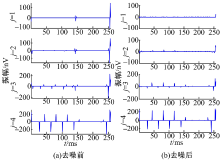
对加入工频噪声的MRS信号进行处理前、后模极大值点的对比如图8所示。与加入白噪声的对比结果类似, 随着分解尺度的增加噪声部分越来越少, 有用信号成为主要部分, 所以保留下来的系数也越来越多。

为了反映基于自适应和小波模极大值重构滤波方法的优越性, 下面给出了几种经过不同滤波方式得到的包络信号和频谱图, 如图9所示。由图可以看出:经自适应和小波模极大值重构滤波后所得到的信号曲线最光滑, 且噪声压制得最低, 信号与噪声分开的效果最好。

对加入噪声的信号进行滤波, 比较滤波前、后情况。核磁共振含噪信号经过不同滤波方法得到特征参数的拟合误差与信噪比的大小以及频谱幅度衰减率的比较结果见表2。

表1 数据经不同滤波方式后的对比(加入白噪声) Table 1 Contrast data with different filtering way(white noise)

滤波方式	振幅 E₀/nV	衰减时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ /ms	相位 φ ₀/(° )	信噪比	拟合误差			频谱幅度衰减率/%
滤波方式	振幅 E₀/nV	衰减时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ /ms	相位 φ ₀/(° )	信噪比	E₀/%		$\begin{matrix} T_{2}^{*} \end{matrix}$ /%	φ ₀/%
理想信号	400	150	165	¥	—	—	—	—
加入白噪声	372.5	164.38	170.9	1.43	—	—	—	—
自适应滤波	395.3	161.03	168.1	1.44	1.17	7.35	1.87	0.47
小波模极大值重构	378.8	163.96	170.0	2.46	5.3	9.3	3.0	0.13
基于自适应和小波模极大值重构	396.7	159.45	167.9	2.61	0.82	6.3	1.75	0.12

表1 数据经不同滤波方式后的对比(加入白噪声) Table 1 Contrast data with different filtering way(white noise)

	Figure Option View Download New Window
	图7 工频噪声包络信号和频谱图Fig.7 Signal envelope and spectrum diagram of industrial frequency noise

	Figure Option View Download New Window
	图8 去噪前后模极大值点对比Fig.8 Contrast before and after of modulus maxima

由表2可以看出, 经过基于自适应的小波模极大值重构处理的数据与另外两种方法相对比, 所得到的特征参数最接近于理想信号, 且信噪比最高。MRS特征参数(振幅E₀, 弛豫时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ , 相位φ ₀)的拟合误差控制在了3%以内, 且频谱幅度衰减率达到0.68%。由加入白噪声所处理的结果分析可知, MRS数据处理之后, 所得到的特征参数

接近于理想信号所对应的特征参数, 说明处理的结果准确, 反演解释结果的可信度高。

结合处理后的信号曲线图与表2可知: 经自适应和小波模极大值重构处理之后所得到的信号曲线的平滑度最好, 可以很好地将噪声与信号分离开来, 信噪比达到最高且最可信。

	Figure Option View Download New Window
	图9 处理之后的包络信号和频谱图Fig.9 Envelope signal and the spectrum diagram after filtering

表2 数据经不同滤波方式后的对比(加入工频噪声) Table 2 Contrast data with different filtering way(power noise)

滤波方式	振幅 E₀/nV	衰减时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ /ms	相位 φ ₀/(° )	信噪比	拟合误差			频谱幅度衰减率/%
滤波方式	振幅 E₀/nV	衰减时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ /ms	相位 φ ₀/(° )	信噪比	E₀/%		$\begin{matrix} T_{2}^{*} \end{matrix}$ /%	φ ₀/%
理想信号	400	150	165	¥	—	—	—	—
加入工频噪声	398.2	154.0	163.2	2.86	—	—	—	—
自适应滤波	399.3	151.1	161.2	14.06	0.17	0.73	2.3	0.97
小波模极大值重构	398.3	153.9	162.3	3.41	0.42	2.6	1.6	0.72
基于自适应和小波模大值重构	399.5	150.8	162.5	18.68	0.12	0.53	1.5	0.68

表2 数据经不同滤波方式后的对比(加入工频噪声) Table 2 Contrast data with different filtering way(power noise)

3 实测数据处理

2005年4月, 核磁组在内蒙古乌拉特地区进行了野外实验, 对野外采集数据应用不同的滤波方法进行数据处理。首先对每个测点的单个脉冲矩进行滤波处理, 再利用处理后的数据得出反演结果。

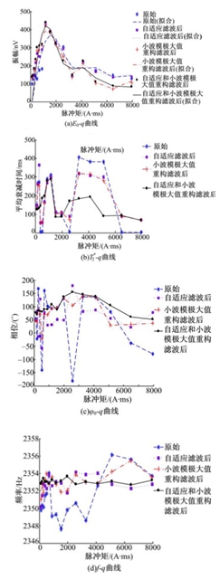(1)测点WLTQ100。当地的拉莫尔频率为2353 Hz, 对原始数据进行处理, 然后提取MRS信号的特征参数E₀、 $\begin{matrix} T_{2}^{*} \end{matrix}$ 、φ ₀、f。由表1可知MRS信号的特征参数所对应的水文地质参数。图10为MRS信号的不同特征参数所对应的曲线。由图可得出, 经自适应和小波模极大值重构滤波后所得到的曲线的平滑度和稳定性最好。

	Figure Option View Download New Window
	图10 不同滤波方式下的MRS信号特征参数曲线Fig.10 MRS signal characteristic parameter curves after different filter methods

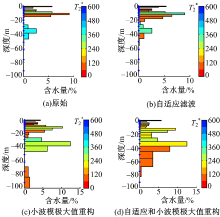
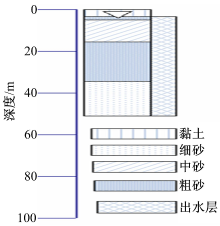
野外试验归纳出的衰减时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ 与含水层的岩性之间有一定的近似关系:T₂< 30 ms时为黏土, 30< T₂< 120 ms时为细砂, 120< T₂< 180 ms时为中砂, 180< T₂< 300 ms时为粗砂。

图11为经过不同滤波方式反演所得到的含水量柱状图。测点WLTQ100距离打井点XF277很近, 为2.03 km, 认为两者的水文地质情况是相似的。XF277的水文地质情况如图12所示。由图可知:XF277打井深度为1.575~50 m, 含水层厚度为48.425 m。饱和含水层从5 m开始, 5~6 m为粗砂, 6~17.9 m为中砂, 17.9~34.9 m为粗砂, 34.9~50 m为细砂。由图11、图12及 $\begin{matrix} T_{2}^{*} \end{matrix}$ 与含水层的岩性关系分析可得, 经自适应和小波模极大值重构反演所得到的含水量柱状图与钻探结果基本相符, 更接近于实际情况。

	Figure Option View Download New Window
	图11 不同滤波后反演所得到的含水量柱状图Fig.11 MRS inversion results with the different methods

	Figure Option View Download New Window
	图12 XF277水文地质情况Fig.12 XF277 hydrological geology

(2)测点WLTQ94。当地的拉莫尔频率为2354 Hz, 与WLTQ100处理过程相同。图13为MRS信号相应的特征参数对应的曲线。从图13中可知:经自适应和小波模极大值重构滤波后所得到的特征曲线的平滑度提高的程度最大, 稳定性最好。

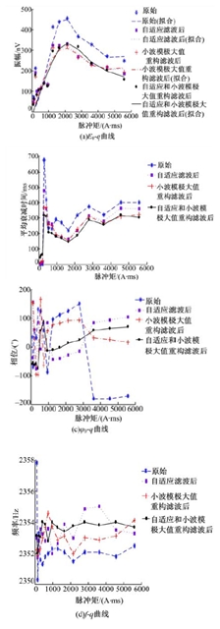	Figure Option View Download New Window
	图13 不同滤波方式下的MRS信号特征参数曲线Fig.13 MRS signal characteristic parameter curves after different filter methods

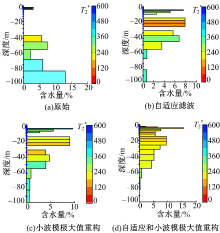
图14为经过不同滤波方式反演所得到的含水量柱状图。测点WLTQ94距离打井点HL11很近, 为3.17 km, 同样两者的水文地质情况是相似的。HL11的水文地质情况如图15所示。由图可知:HL11打井深度为1.5~42 m, 含水层厚度为40.5 m, 出水层从1.5 m开始, 1.5~5 m为粗砂, 5~21.7 m为中砂, 21.7~42 m为粗砂。经图14、图15及 $\begin{matrix} T_{2}^{*} \end{matrix}$ 与含水层的岩性关系的分析得出, 经自适应和小波模极大值重构反演得到的含水量柱状图更接近于钻井的实际情况。

	Figure Option View Download New Window
	图14 不同滤波后反演所得到的的含水量柱状图Fig.14 MRS inversion results with the different methods

	Figure Option View Download New Window
	图15 HL11水文地质情况Fig.15 HL11 hydrological geology

4 结论

(1)MRS特征参数(振幅E₀, 弛豫时间 $\begin{matrix} T_{2}^{*} \end{matrix}$ , 相位φ ₀)的拟合误差控制在了3%以内。由处理的结果分析可知, MRS数据处理之后, 所得到的特征参数接近于理想信号所对应的特征参数, 说明处理的结果准确, 反演解释结果的可信度高。

(2)实测数据处理表明, 在地下水含量未知的条件下对于不同强度的噪声干扰基于自适应和小波模极大值重构算法获得了较好的去噪效果。

(3)通过理想信号加入两种噪声, 经过不同滤波方法的比较, 得出了不同噪声情况下的消噪策略, 实测信号也验证了上述策略的适用性, 为野外试验的数据处理提供了指导, 缩短了寻找最佳方法所用时间, 提高了效率, 对以后消噪方法的研究给出了参考。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Legchenko A, Baltassat J M, Bobachev A, et al. Magnetic resonance sounding applied to aquifer characterization[J]. Ground Water, 2004, 42(3): 363-373. [本文引用:1]
[2]	Legchenko A, Baltassat, J M, Beauce A, et al. Nuclear magnetic resonance as a geophysical tool for hydrogeologists[J]. Journal of Applied Geophysics, 2002, 50(1): 21-46. [本文引用:1]
[3]	Müller-Petke M, Hiller T, Herrmann R, et al. Reliability and limitations of surface NMR assessed by comparison to borehole NMR[J]. Near Surface Geophysics, 2011, 9(2): 123-134. [本文引用:1]
[4]	Vouillamoz J M, Legchenko A, Nand agiri L. Characterizing aquifers when using magnetic resonance sounding in a heterogeneous geomagnetic field[J]. Near Surface Geophysics, 2011, 9(2): 135-144. [本文引用:1]
[5]	Juan Plata, Felix Rubio. MRS experiments in a noisy area of a detrital aquifer in the south of Spain[J]. Journal of Applied Geophysics, 2002, 50(1): 83-94. [本文引用:1]
[6]	Jiang C D, Lin J, Duan Q M, et al. Statistical stacking and adaptive notch filter to remove high-level electromagnetic noise from MRS measurements[J]. Near Surface Geophysics, 2011, 9(5): 459-468. [本文引用:1]
[7]	Konstantinos Chalikakis, Mette Ryom Nielsen, Anatoly Legchenko. MRS applicability for a study of glacial sedimentary aquifers in Central Jutland , Denmark[J]. Journal of Applied Geophysics, 2008, 66(3): 176-187. [本文引用:1]
[8]	Trushkin D V, Shushakov O A, Legchenko A V. The potential of a noise-reducing antenna for surface NMR groundwater surveys in the earth's magnetic field[J]. Geophysical Prospecting, 1994, 42(8): 855-862. [本文引用:1]
[9]	Anatoly Legchenko, Pierre Valla. A review of the basic principles for proton magnetic resonance sounding measurements[J]. Journal of Applied Geophysics, 2002, 50(1): 3-19. [本文引用:1]
[10]	Legchenko A, Valla P. Processing of surface proton magnetic resonance signals using non-linear fitting[J]. Journal of Applied Geophysics, 1998, 39(2): 77-83. [本文引用:1]
[11]	Legchenko A, Valla P. Removal of power-line harmonics from proton magnetic resonance measurements[J]. Journal of Applied Geophysics, 2003, 53(2): 103-120. [本文引用:1]
[12]	Legchenko A. MRS measurements and inversion in presence of EM noise[J]. Boletín Geológico y Minero, 2007, 118(3): 489-508. [本文引用:1]
[13]	Walsh D O. Multi-channel surface NMR instrumentation and software for 1D/2D groundwater investigations[J]. Journal of Applied Geophysics, 2008, 66(3): 140-150. [本文引用:1]
[14]	田宝凤, 段清明. 核磁共振信号工频谐波的自适应滤除方法[J]. 吉林大学学报: 信息科学版, 2009, 27(3): 223-228. Tian Bao-feng, Duan Qing-ming. Removal method of industrial frequency harmonics in nuclear magnetic resonance signal based on adaptive filter[J]. Journal of Jilin University (Information Science Edition), 2009, 27(3): 223-228. [本文引用:2]
[15]	田宝凤, 林君, 段清明, 等. 基于参考线圈和变步长自适应的磁共振信号噪声压制方法[J]. 地球物理学报, 2012, 55(7): 2462-2472. Tian Bao-feng, Lin Jun, Duan Qing-ming, et al. Variable step adaptive noise cancellation algorithm for magnetic resonance sounding signal with a reference coil[J]. Chinese Journal of Geophysics, 2012, 55(7): 2462-2472. [本文引用:2]
[16]	曾亮, 李振宇, 王鹏. 小波分析在提高核磁共振找水信号信噪比中的应用探讨[J]. CT 理论与应用研究, 2007, 15(2): 1-5. Zeng Liang, Li Zhen-yu, Wang Peng. Improveing S/N ratio of MRS signal of detecting ground water with wavelet analysis[J]. CT Theory and Applications, 2007, 15(2): 1-5. [本文引用:1]
[17]	Strehl S, Rommel I, Hertrich M, et al. New strategies for filtering and fitting of MRS signals[C]∥Proc Proceedings 3rd International MRS Workshop, Madrid, Spain, 2006: 65-68. [本文引用:1]
[18]	Strehl S. Development of strategies for improved filtering and fitting of SNMR-Signals[D]. Berlin: Department of Applied Geophysics Diplomarbeit, Institute of Applied Geosciences, Technical University of Berlin, 2006. [本文引用:1]
[19]	Abdullah Al Jumah. Denoising of an image using discrete stationary wavelet transform and various thresholding techniques[J]. Journal of Signal and Information Processing, 2013, 4(1): 33-41. [本文引用:1]
[20]	Nair S S, Joseph K P. Wavelet based electroretinographic signal analysis for diagnosis[J]. Biomedical Signal Processing and Control, 2014(9): 37-44. [本文引用:1]
[21]	张金榜, 孙艺笑, 王润典, 等. 改进的阈值函数去噪算法[J]. 电子科技, 2014, 27(2): 17-20. Zhang Jin-bang, Sun Yi-xiao, Wang Run-dian, et al. An improved threshold denoising algorithm[J]. Electronic Science and Technology, 2014, 27(2): 17-20. [本文引用:1]
[22]	李文刚, 张振勇, 王艳波, 等. 小波分析在矿井高密度电法数据处理中的应用[J]. 中国煤炭地质, 2011, 23(6): 52-55. Li Wen-gang, Zhang Zhen-yong, Wang Yan-bo, et al. Application of wavelet analysis in coalmine high-density electric prospecting data processing[J]. Coal Ceology of China, 2011, 23(6): 52-55. [本文引用:1]
[23]	Sun S, Yang N, Lin J, et al. Adaptive analysis of filter methods for magnetic resonance sounding[C]∥In Digital Manufacturing and Automation (ICDMA), IEEE, 2013: 106-111. [本文引用:1]
[24]	秦毅, 王家序, 毛永芳. 基于软阈值和小波模极大值重构的信号降噪[J]. 振动测试与诊断, 2011, 31(5): 543-547. Qin Yi, Wang Jia-xu, Mao Yong-fang. Based on soft threshold and wavelet modulus maxima reconstruction signal noise reduction[J]. Journal of Vibration, Measurement & Diagnosi, 2011, 31(5): 543-547. [本文引用:1]
[25]	何永红, 文鸿雁, 靳鹏伟. 基于小波模极大值改进算法的变形模型研究[J]. 测绘科学, 2007, 32(4): 18-20. He Yong-hong, Wen Hong-yan, Jin Peng-wei. Deformation of the improved algorithm based on wavelet modulus maxima model research[J]. Science of Surveying and Mapping, 2007, 32(4): 18-20. [本文引用:1]

2004

0.0

... 0 引言核磁共振测水方法是利用地层中丰度最高的氢原子核的顺磁性产生的核磁共振(Magnetic resonance sounding,MRS)信号,通过改变激发电流的大小完成对不同深度地下水的测量^[1,2] ...

2002

0.0

2011

0.0

... 对采集的信号经过滤波处理之后,即可反演解释得到地下含水层深度、厚度、含水量大小、含水层平均孔隙度等信息^[3,4] ...

2011

0.0

... 对采集的信号经过滤波处理之后,即可反演解释得到地下含水层深度、厚度、含水量大小、含水层平均孔隙度等信息^[3,4] ...

2002

0.0

... 国内外专家学者提出了多种方法来抑制噪声,主要有:仪器采集数据的叠加方法^[5,6],缺点在于叠加次数多,系统的工作效率低 ...

2011

0.0

... 国内外专家学者提出了多种方法来抑制噪声,主要有:仪器采集数据的叠加方法^[5,6],缺点在于叠加次数多,系统的工作效率低 ...

2008

0.0

... 探测线圈采用八字形线圈^[7,8]方式,与圆形探测线圈相比,探测深度降低一半 ...

1994

0.0

... 探测线圈采用八字形线圈^[7,8]方式,与圆形探测线圈相比,探测深度降低一半 ...

2002

0.0

... 采用同步检波和FIR低通滤波技术^[9,10]的方法会引起有用信号的失真 ...

1998

0.0

... 采用同步检波和FIR低通滤波技术^[9,10]的方法会引起有用信号的失真 ...

2003

0.0

... 此外还有滑动平均滤波法、区块对消法,正弦对消法、陷波滤波器法^{[11,12,13,14,15,16,17,18]} ...

2007

0.0

... 此外还有滑动平均滤波法、区块对消法,正弦对消法、陷波滤波器法^{[11,12,13,14,15,16,17,18]} ...

2008

0.0

... 此外还有滑动平均滤波法、区块对消法,正弦对消法、陷波滤波器法^{[11,12,13,14,15,16,17,18]} ...

2009

0.0

. 2009, 27(3):223-228 DOI:doi:10.3969/j.issn.1671-5896.2009.03.001

Removal method of industrial frequency harmonics in nuclear magnetic resonance signal based on adaptive filter

核磁共振信号工频谐波的自适应滤除方法

Tian Bao-feng , Duan Qing-ming.

田宝凤, 段清明

摘　要：针对核磁共振测量信号中的噪声，尤其是拉摩尔频率附近的工频谐波噪声干扰问题，采用自适应滤波的方法进行噪声滤除，在自适应滤波去噪基本原理的基础上，对自适应陷波滤波器的性能进行了仿真研究，并将该方法应用到实际采集到的核磁共振信号工频谐波干扰的滤除中。研究结果表明，相对于传统的设计陷波滤波器去噪的方法，自适应陷波器可自动跟踪干扰频率和相角，滤波后信号的失真小，通过包络拟合后，信号振幅和弛豫时间的误差精度较高，可控制在5％以内，从而实现了工频谐波干扰的有效滤除。

... 此外还有滑动平均滤波法、区块对消法,正弦对消法、陷波滤波器法^{[11,12,13,14,15,16,17,18]} ...

... 12%,满足实际应用的要求^[14,15] ...

2012

0.0

. 2012, 55(7):2462-2472 DOI:10.6038/j.issn.0001-5733.2012.07.030

Variable step adaptive noise cancellation algorithm for magnetic resonance sounding signal with a reference coil

基于参考线圈和变步长自适应的磁共振信号噪声压制方法

Tian Bao-feng , Lin Jun , Duan Qing-ming

田宝凤, 林君, 段清明

College of Instrumentation and Electrical Engineering/Key Laboratory of Geo-Exploration and Instrumentation, Ministry of Education, Jilin University, Changchun 130061, China

Due to the high sensitivity of magnetic resonance sounding (MRS) instrument for groundwater exploration, the nV-level MRS signal received from the instrument is susceptible to interference of high industrial frequency harmonics, which leads to accuracy decrease in signal parameter extraction and influences the inversion result. To solve this problem, a 90° phase-shift adaptive noise cancellation system with reference coil for MRS full wave signal, based on the principle of correlation cancellation, is designed in this paper. The distance of reference coil away from the detection coil is theoretically calculated, and the algorithm of variable step adaptive noise cancellation is presented. The simulation results show that with different signal amplitudes and signal to noise ratios (SNR), adopting the adaptive noise cancellation system and variable step algorithm can increase SNR to 5.94dB or above, while the fitting error of initial amplitude and relaxation time is within 2.8%, when industrial frequency harmonics are not in coincidence with the signal frequency. However, when they are in coincidence, SNR can reach 5dB or above and the fitting error of initial amplitude and relaxation time is within 10%. The result of the variable step adaptive noise cancellation algorithm meets the requirement of practical application. Processing of field measured signals further proved the effectiveness of this algorithm.

核磁共振地下水探测仪的灵敏度高,接收到的纳伏级磁共振探测信号极易受到强工频谐波噪声的干扰,导致信号特征参数提取的准确度降低,影响反演解释的水文地质参数结果.为了解决这一难题,基于相关抵消的原理,针对全波磁共振信号,设计带有参考线圈的90°移相自适应噪声抵消系统,理论计算了参考线圈相对于探测线圈的距离,提出变步长LMS算法进行噪声压制.仿真结果表明,在不同的信号强度及不同的信噪比下,当信号与工频谐波干扰频谱不重合时,采用设计的自适应噪声抵消系统和变步长算法,信噪比可以提高到5.94 dB以上,初始振幅、弛豫时间特征参数的拟合误差在2.8%以内;当信号与工频谐波干扰频谱重合时,采用双向自适应滤波算法,信噪比可以达到5dB以上,初始振幅、弛豫时间特征参数的拟合误差在10%以内,可以满足实际应用的要求;实测数据处理进一步证明了方法的有效性.

... 此外还有滑动平均滤波法、区块对消法,正弦对消法、陷波滤波器法^{[11,12,13,14,15,16,17,18]} ...

... 12%,满足实际应用的要求^[14,15] ...

2007

0.0

. 2007, 15(2):1-5 DOI:doi:10.3969/j.issn.1004-4140.2006.02.001

Improveing S/N ratio of MRS signal of detecting ground water with wavelet analysis

小波分析在提高核磁共振找水信号信噪比中的应用探讨

Zeng Liang , Li Zhen-yu , Wang Peng.

曾亮, 李振宇, 王鹏

地面核磁共振(SNMR)找水方法是目前唯一能直接找到地下水的地球物理新方法.由于该方法接收灵敏度高,因此对电磁噪声也很敏感.为了提高信噪比和新方法的找水效果,必须对接收到的信号进行去噪处理.本文使用了小波分析去噪提高核磁共振信号信噪比的方法,并通过对湖北省新洲工区和王家湾工区实测数据的小波处理和对比分析,证明了这种方法的有效性.

... 此外还有滑动平均滤波法、区块对消法,正弦对消法、陷波滤波器法^{[11,12,13,14,15,16,17,18]} ...

2006

0.0

... 此外还有滑动平均滤波法、区块对消法,正弦对消法、陷波滤波器法^{[11,12,13,14,15,16,17,18]} ...

2006

0.0

... 此外还有滑动平均滤波法、区块对消法,正弦对消法、陷波滤波器法^{[11,12,13,14,15,16,17,18]} ...

2013

0.0

... 本文研究了自适应和小波模极大值重构方法,自适应滤波方式主要是针对固定频率噪声的滤波处理,小波模极大值重构方法主要是针对白噪声的滤波处理^{[19,20,21,22]} ...

0.0

2014

0.0

. 2014, 27(2):17-20 DOI:doi:10.3969/j.issn.1007-7820.2014.02.006

An improved threshold denoising algorithm

改进的阈值函数去噪算法

Zhang Jin-bang , Sun Yi-xiao , Wang Run-dian

张金榜, 孙艺笑, 王润典

An improved threshold denoising algorithm was proposed aiming at the problem of the invariable warp existing in flexible threshold and setting zero when the quotiety of wavelet was smaller existing in forcedly threshold.This algorithm has used exponent function to improve the threshold function came to the advantages of the flexible threshold.The simulation results show that denoised speech signal-to-noise ratio larger improvement,smoother signal,lower distortion,sharper noise reduction when compared with traditional algorithm.

针对软、硬阈值函数存在的恒定偏差以及在小波系数较小时置零的问题,提出了改进的阈值函数去噪算法。该算法在继承了软阈值函数优点的基础上,利用指数函数改进阈值函数。实验表明,改进的算法降噪后的语音信噪比显著提高、降噪效果明显、信号波形更加平滑、且失真度小。

2011

0.0

. 2011, 23(6):52-55 DOI:doi:10.3969/j.issn.1674-1803.2011.06.13

Application of wavelet analysis in coalmine high-density electric prospecting data processing

小波分析在矿井高密度电法数据处理中的应用

Li Wen-gang , Zhang Zhen-yong , Wang Yan-bo

李文刚, 张振勇, 王艳波

矿井高密度电阻率法数据由于受地电干扰、地形、接地电阻等因素的影响,通常会遇到具有一定平尺度和垂向幅度的类似尖脉冲假异常.在数据处理过程中,对于高幅度和宽尺度的噪声,特别是与有用信息的幅度及尺度相近时,即使应用广泛的Donoho软阈值函数和硬阈值函数去噪,也存在着难以克服的问题.为此提出了一种基于线性软阈值的去噪方法:根据噪声尺度确定分解层数,而每一层的阈值则采用线性函数确定.通过实测资料分析可知,这种方法能有效消除高频随机噪声和特定尺度的噪声,尤其是在处理类似尖脉冲的噪声信号时有较好的效果,同时能较好地保持原有地质信息.

2013

0.0

... 的工频谐波干扰时,利用自适应滤波器可以消除这种特定频率成分的干扰,自适应滤波器结构图^[23]如图2所示 ...

2011

0.0

. 2011, 31(5):543-547 DOI:doi:doi:10.3969/j.issn.1004-6801.2011.05.001

Based on soft threshold and wavelet modulus maxima reconstruction signal noise reduction

基于软阈值和小波模极大值重构的信号降噪

Qin Yi , Wang Jia-xu , Mao Yong-fang.

秦毅, 王家序, 毛永芳

软阈值小波降噪是一种常用的非平稳信号特征提取方法。为了改进软阈值小波降噪法的性能,提出一种基于软阈值和二进小波变换模极大值的新小波降噪方法。首先,对信号进行二进小波变换,再对小波系数进行软阈值处理;然后,选择由信号产生的小波系数模极大值点;最后,用交替投影算法重建信号。理论分析表明,该方法能有效地降低软阈值小波降噪法的误差下界。仿真试验表明,该方法提高了降噪结果的信噪比,且较好地保留了信号中的奇异性。将该方法和二进小波变换软阈值降噪法结合起来,应用于滚动轴承故障振动信号降噪。结果表明,该方法能有效地提取到信号中的冲击特征。

... L²(R),则这一信号的二进小波变换定义为^[24]: ...

2007

0.0

. 2007, 32(4):18-20 DOI:doi:10.3771/j.issn.1009-2307.2007.04.006

Deformation of the improved algorithm based on wavelet modulus maxima model research

基于小波模极大值改进算法的变形模型研究

He Yong-hong , Wen Hong-yan , Jin Peng-wei.

何永红, 文鸿雁, 靳鹏伟

变形监测中获得的观测资料不可避免地存在着噪声,如何从受噪声干扰的数据序列中提取特征信息,提高变形监测的精度是变形监测系统所涉及的关键技术问题之一.本文把小波模极大值与变形监测相结合,给出了改进的小波模极大值变形监测模型.该模型把阈值去噪和Witkin尺度跟踪理论结合,有效恢复了信号.与传统的去噪方法相比,该算法有着更高的精度,提高了信噪比,有更好的去噪效果.

... 小波模极大值重构算法的主要优点是根据小波变换系数模极大值的跨尺度传播规律,可以明确区分每一分解层次上代表噪声和信号的小波变换系数,既不会去掉微弱的有用信号,也不会保留强度较大的噪声^[25] ...