三维无线多媒体传感器网络全目标覆盖算法

引用本文

王艳娇, 毕晓君, 滕志军, 邬春明. 三维无线多媒体传感器网络全目标覆盖算法. 2015, 45(5): 1671-1679
WANG Yan-jiao, BI Xiao-jun, TENG Zhi-jun, WU Chun-ming. Coverage-all targets algorithm of directional sensor network for three-dimensional perception. Journal of Jilin University Engineering and Technology Edition, 2015, 45(5): 1671-1679 复制到剪切板

Permissions

三维无线多媒体传感器网络全目标覆盖算法

王艳娇^1,², 毕晓君², 滕志军¹, 邬春明¹

1.东北电力大学信息工程学院,吉林省吉林市 132012

2.哈尔滨工程大学信息与通信工程学院,哈尔滨 150001

作者简介:王艳娇(1985-),女,副教授,博士.研究方向:无线多媒体传感器网络目标覆盖算法及智能信息处理.E-mail:wangyanjiao1028@126.com

基金:国家自然科学基金项目(61175126); 东北电力大学博士科研启动基金项目(BSJXM-2013-20)

摘要

针对现有感知模型无法有效描述无线多媒体传感器真实感知能力的缺陷,提出一种新的三维有向感知模型。在此基础上,针对目标覆盖问题,为降低算法复杂度,设计了一种基于仰俯角优化和偏向角优化的两阶段目标覆盖算法。对于仰俯角和偏向角优化部分,利用差分进化算法进行求解,以达到利用少量传感器节点实现监测目标被全部覆盖的效果。仿真实验表明:对比随机部署方法,本文方法所需的传感器数目大幅下降。

关键词: 通信技术; 三维有向感知模型; 无线多媒体传感器网络; 目标覆盖

中图分类号:TN912 文献标志码:A 文章编号:1671-5497(2015)05-1671-09

Coverage-all targets algorithm of directional sensor network for three-dimensional perception

WANG Yan-jiao^1,², BI Xiao-jun², TENG Zhi-jun¹, WU Chun-ming¹

1.College of Information Engineering,Northeast Dianli University, Jilin 132012, China

2.College of Information and Communication Engineering,Harbin Engineering University, Harbin 150001, China

Abstract

The existing traditional perception models can not characterize the real perception ability of wireless multimedia sensor node accurately. To overcome this shortcoming a novel three-dimensional directional perception model is proposed. On this basis, a target coverage algorithm is designed based on the optimization of tilt angle and deviation angle instead of adjusting the main perception directions to solve the all targets coverage problem. The title angle and deviation angle are optimized based on differential evolution algorithm in order to use fewer sensors to cover all targets. Simulation results show that the proposed method requires less number of sensors to cover all targets than random deployment.

Keyword: communication technology; three-dimensional perception; wireless multimedia directional sensor networks; targets coverage problem

Show Figures

0 引言

随着无线多媒体传感器网络(Wireless multimedia sensor networks, WMSNs)研究的深入和实际应用的扩展^{[1, 2, 3]}, 为增强相应覆盖控制算法的实用性和有效性^{[4, 5]}, 一些学者致力于构建能够描述无线多媒体传感器节点真实感知能力的感知模型。Ma等^[6]于2005年首先设计了基于节点坐标、感知半径、感知方向和感知角度的扇形感知模型, 此后, Makhoul等^{[7, 8]}先后提出三角形和凸多边形感知模型。其中, 扇形感知模型能够较好地描述节点感知性能并且最为简单, 是目前最具代表性、应用最多的一种感知模型, 但是这些二维有向感知模型由于受到空间局限性以及与真实三维环境之间存在本质差别等因素的影响, 无法准确描述节点的空间感知能力, 使得基于此展开的覆盖控制方法与实际应用之间存在不小的技术偏差。基于此, 某些研究者试图建立面向真实环境的更为准确的三维有向感知模型, 如:Ma等^[9]于2009年首次提出基于传感器节点位置、主感知方向、水平方向感知范围和垂直方向感知范围的多媒体传感器节点三维感知模型; 文献[10]对上述模型进行改进, 将主感知方向正交分解为仰俯角和偏向角, 大幅降低了计算复杂度。

上述三维有向感知模型虽已具备一定的空间刻画能力, 但是其空间覆盖区域与传感器的高度无关, 且当其处于某些主感知方向时在二维平面内的覆盖区域没有边界限制, 不符合人们的主观认知, 此外, 无法适应实际三维物理环境的不规则表面覆盖等问题, 还不能准确描述节点的感知性能。为此, 本文提出一种新的三维有向感知模型。在此基础上, 针对典型目标覆盖问题^[11], 即求出覆盖全部目标所需的最小传感器数目, 设计了一种基于仰俯角优化和偏向角优化的新型目标覆盖算法。仿真结果表明:对比随机部署的方法, 本文方法所需的传感器数目大幅下降且比较稳定。

1 新型三维有向感知模型

多媒体传感器节点处于三维物理场景, 节点仅能覆盖球形区域的一部分。本文受传统传感器节点的三维模型建立方式(即将二维平面内的圆节点模型旋转拓展至空间得到球形三维感知模型)的启发^[12], 将多媒体传感器感知模型中应用最广的扇形模型绕节点旋转一定角度构建新型多媒体传感器三维有向感知模型, 具体定义如下:

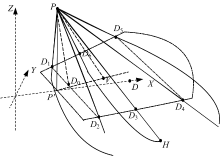
定义1 多媒体传感器三维有向感知模型可用一个五元数组(P, C, α , β , R)表示, 其中, C为主感知方向(与Z轴夹角称为仰俯角γ , 在X-Y平面投影为偏向角θ ), 2α 、2β 和R分别为水平感知角度(水平视域)、垂直方向感知角度(垂直视域)和感知半径。

为充分理解本文所提三维有向感知模型的定义, 这里给出其具体描述如图1所示。

	Figure Option View Download New Window
	图1 新的三维感知模型Fig.1 Novel three-dimensional directional perception model

图1中, $\begin{matrix} \vec{PV} \end{matrix}$ =C, ∠P'PV=γ , ∠VP'D=θ , ∠VPD₀=β , PH=R, ∠VPD₆=α 。

由上述模型可见, 其在二维平面内的最大覆盖范围为距点P'(P在X-Y平面内投影) $\begin{matrix} \sqrt[]{R^{2} - z^{2}} \end{matrix}$ 以内, 且随着传感器被放置高度的增加, 覆盖范围逐渐减小, 符合人们的主观认知, 充分克服了现有两种三维有向感知模型的缺陷, 能够更加真实地描述节点感知能力。

2 面向新型三维有向感知模型的目标覆盖问题

定义2 本文研究的目标覆盖问题是指, 为实现对二维平面内存在的N个目标的全面有效监测, 在三维场景中随机布撒M个参数完全相同的传感器, 求出覆盖所有目标需要开启工作的最少传感器数目。

对应于本文提出的三维有向感知模型, 影响节点覆盖能力的可控变量为主感知方向, 那么相应的目标覆盖算法就是求解包含仰俯角和偏向角的一个最优组合[(γ ₁, θ ₁), (γ ₂, θ ₂), …, (γ _M, θ _M)], 在覆盖所有目标的同时, 所用变量数目最少。

为了便于数学分析, 这里给出其相应的数学定义, 具体如下:

$\begin{matrix} \{\begin{matrix} \min |S'| \\ a ≺ S', \forall a \in A, S' \subseteq S \\ \overset{\infty}{\sum_{j = 0}} \overset{\infty}{\sum_{k = 0}} x_{ijk} \leq 1, \forall s_{i} \in S' \end{matrix} (1) \end{matrix}$

式中:S'为所选的传感器集合; A和S分别为目标集合和传感器集合; a为某目标; x_ijk为传感器i工作在仰俯角j和偏向角k的主感知方向上。约束条件保证所有目标都被覆盖以及每个传感器至多工作在一个方向上。

确定目标是否被节点覆盖是从数学上解决覆盖问题的关键, 为此, 这里需明确本文提出的三维有向感知模型的目标覆盖条件。

按照该模型的定义, 其在水平监测区域的投影相当于一个扇形绕顶点旋转后的横截面, 具体如图2所示。

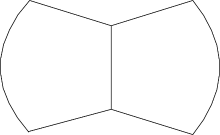	Figure Option View Download New Window
	图2 三维有向感知模型的横截面图Fig.2 Cross-sectional figure of novel three-dimensional directional perception model

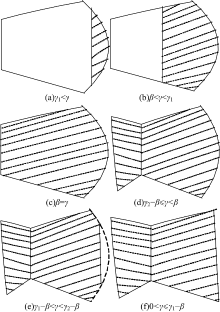
受到α 和β 的限制, 不同的仰俯角只会获得如图2所示的图形中的一部分, 通过推导发现水平监测区域会出现如图3所示的6种投影图形。

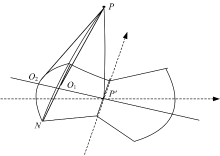
	Figure Option View Download New Window
	图3 水平投影情况Fig.3 Horizontal projection situation

图3中γ ₁和γ ₂分别对应于如图4所示的两种临界状态, 满足如下关系:

$\begin{matrix} \begin{matrix} \cos γ_{1} = \cos ∠ P' P O_{1} = \frac{PP'}{P O_{1}} = \frac{z}{Rcosα} \\ \cos γ_{2} = \cos ∠ P' P O_{2} = \frac{PP'}{P O_{2}} = \frac{z}{R} \end{matrix} \end{matrix}$

	Figure Option View Download New Window
	图4 临界条件示例Fig.4 Critical condition

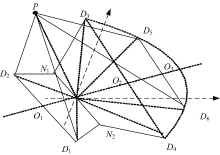
限于篇幅, 这里仅以最为复杂的投影图形(图3(e))为例说明目标节点的覆盖判别方法。为便于分析说明, 给出图3(e)相应的空间位置分布, 如图5所示。其中, ∠P'PO3=γ +β 、PP'=z、∠P'PO1=β -γ 、PD4=PD6=R、∠D₁PO₁=∠N₂PP'=∠D₄PO₂=∠D₆PO₃=α 。

	Figure Option View Download New Window
	图5 图3(e)的空间信息Fig.5 Spatial information of Fig.3(e)

判断目标是否被节点覆盖的方法如下:在满足式(2)的基础上, 位于D₅D₃N₁N₂D₄D₆内部(即在有向线段D₅D₆的右侧、有向线段N₁D₃右侧、N₁N₂左侧及N₂D₄左侧), 或处于四边形D₁D₂N₁N₂内(在有向线段D₁D₂右侧、D₂N₁右侧、N₁N₂右侧及N₂D₁右侧)。

$\begin{matrix} {x_{0}}^{2} + {y_{0}}^{2} \leq R^{2} - z^{2} (2) \end{matrix}$

以判断目标T(X', Y')在有向线段D₅D₆左侧或右侧为例说明判别上述位置关系的实施方法, 具体如下:目标T关于P'的相对坐标为T'(X'-x, Y'-y)=T'(x₀, y₀), D₅、D₆的坐标分别记为( $\begin{matrix} x_{D_{5}} \end{matrix}$ , $\begin{matrix} y_{D_{5}} \end{matrix}$ )、( $\begin{matrix} x_{D_{6}} \end{matrix}$ , $\begin{matrix} y_{D_{6}} \end{matrix}$ )。若D₁> 0, 在有向线段D₅D₆的右侧; 否则在该有向线段左侧。其中, A₁= $\begin{matrix} y_{D_{6}} \end{matrix}$ - $\begin{matrix} y_{D_{5}} \end{matrix}$ 、B₁= $\begin{matrix} x_{D_{5}} \end{matrix}$ - $\begin{matrix} x_{D_{6}} \end{matrix}$ 、C₁= $\begin{matrix} x_{D_{6}} \end{matrix} \begin{matrix} y_{D_{5}} \end{matrix}$ - $\begin{matrix} x_{D_{5}} \end{matrix} \begin{matrix} y_{D_{6}} \end{matrix}$ 、D₁=A₁x₀+B₁y₀-C₁。

为实施上述目标覆盖方案, 必须明确图5中处于二维平面内的相应各点坐标, 具体如下:

D₁ $\begin{matrix} (P' D_{1} \cos (π + θ + A), P' D_{1} \sin (π + θ + A)) \end{matrix}$

D₂ $\begin{matrix} (P' D_{1} \cos (π + θ - A), P' D_{1} \sin (π + θ - A)) \end{matrix}$

N₁ $\begin{matrix} (P' N_{1} \cos (\frac{π}{2} + θ), P' N_{1} \sin (\frac{π}{2} + θ)) \end{matrix}$

N₂ $\begin{matrix} (P' N_{1} \cos (\frac{3 π}{2} + θ), P' N_{1} \sin (\frac{3 π}{2} + θ)) \end{matrix}$

D₃ $\begin{matrix} (P' D_{4} \cos (B + θ), P' D_{4} \sin (B + θ)) \end{matrix}$

D₄ $\begin{matrix} (P' D_{4} \cos (θ - B), P' D_{4} \sin (θ - B)) \end{matrix}$

D₅ $\begin{matrix} (P' D_{6} \cos (C + θ), P' D_{6} \sin (C + θ)) \end{matrix}$

D₆ $\begin{matrix} (P' D_{6} \cos (C - θ), P' D_{6} \sin (C - θ)) \end{matrix}$

其中:

tanA=tan∠D₁P'O₁= $\begin{matrix} \frac{O_{1} D_{1}}{O_{1} P'} \end{matrix}$ = $\begin{matrix} \frac{tanα}{\sin (β - γ)} \end{matrix}$ ,

sinB=sin∠D₄PO₂= $\begin{matrix} \frac{D_{4} O_{2}}{D_{4} P'} \end{matrix}$ = $\begin{matrix} \frac{Rsinα}{\sqrt[]{R^{2} - z^{2}}} \end{matrix}$ ,

cosC=cos∠D₆P'O₃= $\begin{matrix} \frac{P' O_{3}}{P' D 6} \end{matrix}$ = $\begin{matrix} \frac{ztan (β + γ)}{\sqrt[]{R^{2} - z^{2}}} \end{matrix}$ ,

P'D₄= $\begin{matrix} \sqrt[]{R^{2} - z^{2}} \end{matrix}$ , P'N₁=ztanα ,

P'D₁= $\begin{matrix} \sqrt[]{P' {O_{1}}^{2} + O_{1} {D_{1}}^{2}} \end{matrix}$ = $\begin{matrix} \frac{z \sqrt[]{si n^{2} (β - γ) + ta n^{2} α}}{\cos (β - γ)} \end{matrix}$ 。

3 面向新型三维有向感知模型的目标覆盖算法

对于本文设计的多媒体传感器三维感知模型, 为实现所有目标的有效覆盖, 如果直接同时优化主感知方向中的仰俯角和偏向角, 复杂度过高, 对算法效率等要求过高, 难以求得满意结果。考虑到主感知方向中的仰俯角γ 影响其在水平方向的投影覆盖面积, 偏向角θ 影响其投影图形的朝向。如果调整仰俯角γ 保证每个传感器在水平方向的覆盖面积最大, 就可以使每个传感器覆盖尽可能多的目标, 再综合调整各传感器投影图形的朝向, 就可以达到目标覆盖算法的要求, 即用尽量少的传感器覆盖所有的目标, 复杂度大幅降低。基于上述分析, 将目标覆盖算法分成仰俯角优化和偏向角优化两部分。

3.1 仰俯角优化

仰俯角γ 的大小决定传感器在水平方向的投影覆盖面积大小, 投影覆盖面积越大, 传感器所能覆盖的目标就会越多, 越有利于用较少的传感器覆盖所有的目标。这里把投影覆盖面积达到最大的仰俯角称为最优仰俯角。

由图3中的三维感知模型的水平投影情况可以看出, 当γ ₂< 2β 时, 只会出现图3(a)(b)的情况, 投影面积最大时对应图3(b)的情况, 此时, γ +β =γ ₂, 即γ =γ ₂-β ; 而当γ ₂> 2β 时, 投影面积最大应出现在图3(d)(e)和(f)中, 而图3(d)(f)对应的最佳仰俯角为γ =γ ₂-β 和γ =γ ₁-β , 可以看作是图3(e)的边界情况。为此仅计算图3(e)面积即可求出最优仰俯角。

由图3(e)的空间位置关系(见图5)可得到其在二维平面内的投影图形的面积计算公式, 具体表述为:

$\begin{matrix} \begin{matrix} S = S_{梯 D_{1} D_{2} N_{1} N_{2}} + S_{扇 D_{3} P' D_{4}} - \\ S_{扇 D_{5} P' D_{6}} + S_{△ D_{5} P' D_{6}} + 2 S_{△ N_{2} P' D_{4}} = \\ \frac{1}{2} (N_{2} N_{1} + D_{1} D_{2}) P' O_{1} + \frac{B}{2 π} π (P' D_{4})^{2} - \\ \frac{C}{2 π} π (P' D_{4})^{2} + \frac{P' O_{3} \times D_{5} D_{6}}{2} + \\ P' N_{2} \times P' D_{4} \cos (B) = \\ [\frac{z}{\cos (β - γ)} tanα + ztanα] ztan (β - r) + \\ \frac{B - C}{2} (R^{2} - z^{2}) + ztan (β + γ) \cdot \\ \sqrt[]{R^{2} - \frac{z^{2}}{co s^{2} (β + r)}} + ztanα \times \sqrt[]{R^{2} co s^{2} α - z^{2}} (3) \end{matrix} \end{matrix}$

式(3)是非线性的复杂函数, 传统数学方法(如梯度下降法、最小二乘法等)很难求得理想结果, 进化算法由于不受函数形式限制, 越来越多地应用于此类问题的求解。差分进化算法^[13]就是该领域最具前沿、最有代表性的算法, 大量实验及文献指出该方法的连续函数优化性能已超越现有较为优秀的遗传算法、粒子群算法等, 为此, 这里采用差分算法求解最优γ 使S最大。

3.2 偏向角优化

经仰俯角优化后, 各个传感器节点都具有固定的、最大覆盖面积的投影图形, 如果随机获取偏向角, 某些节点很可能未覆盖任何目标或者相邻的多个节点覆盖相同目标, 造成资源浪费, 不符合目标覆盖算法的设计要求。为此, 必须优化偏向角调整各节点的投影图形朝向, 它的调整受到相邻节点的彼此制约, 是一个非常复杂的NP-Hard问题。其数学本质是优化各个传感器节点的偏向角, 在这种状态下, 挑选其中的kk个传感器(kk最小)实现覆盖全部目标的目的。鉴于差分进化算法的优化优势, 这里也采用该方法优化节点偏向角。该问题与普通优化问题不同的是, 其适应度函数不具有明确的数学形式。为此, 本文根据实际需求建立如下两种适应度函数求解方式。

方式一:利用进化算法求解。

基于上述分析可知, 该问题的适应度为挑选最优的部分传感器实现目标覆盖, 可以通过如下方式实现:优化传感器顺序, 达到所有目标被完全覆盖的前kk个传感器就是该问题最终选择的传感器组合, 而kk就是适应度值。这一实现方式本身就是一个组合优化的过程, 对于此类问题, 现在广泛采用遗传算法(Genetic algorithm, GA)进行求解, 鉴于该问题与TSP问题的本质相似性, 对于各种改进GA, 这里选用实数编码、交换序交叉操作的遗传算法^[14]求取适应度值。

方式二:随机计算。

随机计算的方式如下:设置一定的循环次数, 在每次循环中, 随机产生一个传感器顺序, 从第一个传感器开始, 逐个保留使覆盖目标增多的传感器, 直至达到所有目标被有效覆盖, 参与计算的传感器数目就是该问题的适应度值。

对比两种适应度计算方式可以发现:方式一的结果更为准确, 但是计算复杂、耗时长、不适宜大规模问题的求解; 方式二的结果虽然不一定是最优的, 但是计算简单, 适合于大规模问题的求解。因此, 在大规模目标覆盖问题的求解中采用方式二计算适应度, 而对于小规模目标覆盖问题或对时间要求不高时, 选用方式一精确计算适应度值。

3.3 目标覆盖算法

利用优化算法实现面向三维有向感知模型的无线多媒体传感器网络的目标覆盖的步骤具体如下:

步骤1 初始化相关参数:区域边界D; 传感器相关参数, 包括β 、α 、γ 和θ 的取值范围及传感器数目M; 目标数目N; 种群数目PN; 迭代次数Maxiter等。

步骤2 在区域内随机布撒传感器及目标。

步骤3 按3.1节中方法优化各传感器仰俯角, 得到最优仰俯角集合{γ ₁, γ ₂, …, γ _M}。

步骤4 初始化遗传算法相关参数, 产生有关传感器偏向角的初始种群。

步骤5 采用3.2节中方法计算适应度值, 即该种已定偏向角配合状态下, 达到目标覆盖所需的最少传感器数目。

步骤6 按照DE/current-to-best/1模式以及逐维单点交叉策略进行变异操作和交叉操作, 得到新个体。

步骤7 按3.2节计算新个体的适应度值, 并将其与原目标个体比较, 保留适应度值更优个体。

步骤8 结合全部更优个体形成新的迭代种群。

步骤9 判断是否满足终止条件, 若满足, 则输出传感器编号及相应仰俯角、偏向角; 若不满足, 则转至步骤6。

4 算法测试及结果分析

为充分验证本文提出的面向三维感知的无线多媒体传感器网络的目标覆盖算法的有效性和先进性, 这里进行了大量实验, 所有实验在硬件配置为Intel Centrino Duo, CPU:T7250、1G内存、主频为2.0 GHz的计算机上进行, 程序采用MATLAB R2007编写。主要包括以下几方面内容:①本文提出的算法能够解决目标覆盖问题; ②验证本文所提两阶段目标覆盖方法的有效性; ③将本文提出的目标覆盖与其他几种部署方法进行比较, 说明本文方法的先进性。

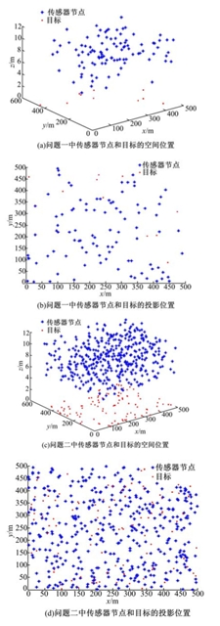
实验场景与文献[10]一致:监测区域为500 m× 500 m的矩形区域, 传感器参数完全相同, 仰俯角γ ∈ $\begin{matrix} [0, π / 2] \end{matrix}$ , 偏向角θ ∈ $\begin{matrix} [0, 2 π] \end{matrix}$ , 水平感知视角和垂直感知视角均为120° , 感知半径为100 m, 随机布撒传感器节点数目为M, 高度信息z∈ [5, 12], 覆盖N个目标。

实验一验证能有效解决目标覆盖问题不失一般性, 这里模拟两个目标覆盖问题, 随机布撒参数完全相同的传感器节点和目标, 问题一和问题二中传感器数目和目标数目分别为100、10和400、100。这两个问题中传感器和目标位置如图6所示。

	Figure Option View Download New Window
	图6 传感器节点和目标节点的位置Fig.6 Position of the senor node and the target node

对于上述两个目标覆盖问题, 利用本文算法优化后, 所调用的传感器在水平面的投影及相应覆盖的目标如图7所示。

	Figure Option View Download New Window
	图7 本文算法处理目标覆盖问题的效果Fig.7 Effect of the proposed targets coverage algorithm

本文算法参数设置如下:种群数目和迭代次数分别为50和100, 对于小规模目标覆盖问题, 即目标数目为10时, 选用3.2节中方法一作为适应度计算方式, 而对于目标数目为100的大规模覆盖问题, 适应度计算方式选为3.2节中方法二。

从图7可以看出:经本文算法调整以后, 对于小规模目标覆盖问题, 即目标数目为10时, 仅用5个传感器就能实现目标覆盖; 而对于大规模目标覆盖问题, 即目标数为100时, 仅需要28个传感器就可实现目标覆盖。

由此可见, 本文算法能够解决目标覆盖问题。

实验二验证两阶段目标覆盖方法的有效性

为验证本文所提分步优化仰俯角和偏向角的目标覆盖策略的有效性, 将其与综合调整主感知方向(即同时优化偏向角和仰俯角)的目标覆盖方法进行比较。

固定目标数N为10、20、30至100的位置, 在各目标位置下传感器数目都为200, 两种方法都采用3.2节中方法二计算适应度值, 其中, 综合调整主感知方向的方法是指对俯仰角和偏向角统一进行优化。

鉴于公平性原则, 当两种算法处理相同问题时, 即传感器数目和目标数目相同时, 保持传感器和目标的位置相同, 且保证算法的函数评价次数相同, 此外, 为避免随机性对算法评价造成的不良影响, 各算法都独立运行10次。本文算法的参数设置如下:种群数目为50, 迭代次数为100。在各种情况下, 综合调整主感知方向的方法以及本文所提算法覆盖所有目标所需的传感器节点数目如图8所示。

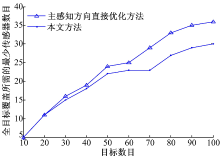
	Figure Option View Download New Window
	图8 两种方法的性能比较Fig.8 Comparison of the performance of two methods

从图8可以看出:在覆盖少量目标时(如目标为10和20时), 本文采用分别优化仰俯角和偏向角的目标覆盖方法与直接调整主感知方向的方法所需传感器数目相同, 而随着目标数目的增多, 本文方法所需传感器数目明显减少, 且目标数目越多优势越明显。这是由于对于不太复杂的小目标覆盖问题, 直接优化主感知方向的方法复杂度不是很高, 一般方法尚且能够满足其复杂度要求, 可求得较好结果, 然而对于复杂情况, 该方法的复杂度过高, 对算法效率及运行机制要求过高, 一般方法很难求得优异结果, 而经本文方法简化后, 复杂度大幅降低, 即可求得更佳结果。

综上所述, 对于复杂的目标覆盖问题, 与直接优化主感知方向的方法相比, 本文所提仰俯角和偏向角分别优化的目标方法更为有效。

实验三验证本文方法的先进性

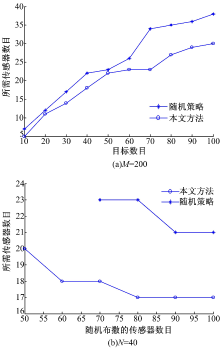
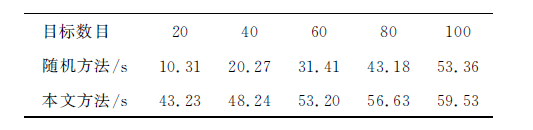
鉴于目前并未见到基于三维有向感知模型的目标覆盖算法相关成果发表, 这里仅能将本文方法与随机部署方法进行比较, 其中, 随机部署方法是指俯仰角、偏向角在规定范围内随机变化, 在某种部署状态下, 覆盖所有目标所需的最少传感器节点数目。为保证对比的全面性和完整性, 这里进行复杂度和覆盖效果两方面的对比。对于时间复杂度的比较, 限于篇幅, 仅统计传感器数目为200, 目标数目分别为20、40、60、80及100时的算法运行时间。为对比的公平性, 保证两种方法的函数评价次数均为2000, 两种方法的时间复杂度比较如表1所示。为充分对比两种算法的覆盖效果, 这里进行大量实验, 参数设置及实验方式与实验二相同, 比较结果如图9所示。

表1 传感器数目为200时两种方法的时间复杂度比较 Table 1 Comparison of time complexity of the number of sensors=200

由表1中数据可以看出:无论是随机方法还是本文方法, 随着目标数目的增多, 算法的运行时间都有所增加, 这是符合实际情况的。无论对于哪种目标覆盖情况, 与随机方法相比, 本文方法所需的时间都略长, 但相差不大, 且目标数目越多, 两者之间的差别越少。

	Figure Option View Download New Window
	图9 两种方法的性能比较Fig.9 Comparison of the performance of two methods

由图9可以得到以下结论:①目标数目相同时(见图9(b)), 无论是随机部署还是本文所提算法, 当传感器数目增加时, 所需的传感器数目都会减少, 这是因为当传感器部署密度增大时, 会使一些传感器的某些方向更加“ 优秀” , 即占据更好的位置, 从而能覆盖更多的目标点并使许多边缘目标点集中化; ②布撒相同数目传感器节点时(见图9(a)), 目标数目越多, 达到目标覆盖所需的传感器数目也越多, 这与实际情况也是一致的; ③无论上述哪种覆盖情况本文方法所需的传感器数目都比随机部署要少, 特别地, 当目标数目为40、随机抛撒传感器数目为50或60时, 随机方法很难实现全目标覆盖, 而本文方法可以求得较为满意的结果, 且情况越为复杂, 本文算法的优越性越明显。

综上所述, 与随机部署方法相比, 本文建立的基于仰俯角和偏向角优化的两阶段目标覆盖算法所需时间略长, 但覆盖效果的优势十分明显。

为进一步验证本文采用差分进化算法对仰俯角和偏向角进行优化的正确性, 将其与模拟退火方法、遗传方法以及粒子群算法进行比较。固定目标数N为25、75和125的位置, 在各目标位置下改变传感器数目为150、250和350, 模拟不同的目标覆盖问题。具体参数设置及实验方式同上, 其性能比较结果(包括算法精度、效率和稳定性)如表2所示。

表2 四种目标覆盖方法的性能比较 Table 2 Comparison of performance of four targets coverage algorithms

从表2中数据可以得出以下结论:

(1)在所求解精度方面, 当覆盖目标数目较少时(如目标数目为25), 本文方法所需传感器数目明显比其他3种方法更少, 而随着目标数目的增加, 4种方法所用传感器数目相差不大, 本文算法所需数目略少, 说明本文方法在覆盖效果方面具有一定优势。这是由于在目标数目较少时, 本文方法由于自身运行机制较好, 能够突破其他几种方法在一定程度上陷入局部最优的僵局、并快速收敛到较优结果, 而随着目标数目的增多, 问题复杂度急剧增高, 对算法要求也越高, 几种方法的运行效率都有所下降。

(2)在稳定性方面, 本文方法在处理小目标覆

盖问题(如目标数目为25)时, 算法十分稳定, 每次都能取得最优结果, 而对于大目标覆盖问题, 与其他3种方法的方差相差不大, 都较小, 说明本文方法相对十分稳定。

(3)在运行效率方面, 对于相同的覆盖问题, 在相同函数评价次数内, 本文方法的运行时间明显小于其他3种方法, 说明本文方法在运行效率方面优势明显。

综上所述, 与采用其他方法执行进化策略的目标方法相比, 本文方法能更为稳定地获得优异结果, 且在运行效率方面优势明显, 说明了本文选择差分进化算法作为进化策略构建目标覆盖算法的正确性。

5 结束语

鉴于现有的多媒体传感器网络目标覆盖算法都是针对理想的二维感知模型设计的, 其理论研究结果与实际应用之间存在较大的技术偏差, 本文从实际角度出发, 在现有三维感知模型中加入感知范围, 提出一种新型三维感知模型, 并设计了一种基于仰俯角优化和偏向角优化的目标覆盖算法。实验仿真结果表明, 与随机部署方法相比, 本文方法能够用更少的有向传感器节点实现所有目标的覆盖。由此可见, 本文提出的目标覆盖算法能够有效解决目标覆盖问题, 具有一定的工程应用前景。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Khuntia P, Pattnaik P K. Target coverge management protocol for wireless sensor network[J]. Journal of Theoretical and Applied Technology, 2012, 35(1): 20-25. [本文引用:1]
[2]	Yang L, Xin H. Research on key technologies to target coverage algorithm in wireless sensor networks[J]. International Journal of Digital Content Technology and its Applications, 2012, 6(17): 542-550. [本文引用:1]
[3]	凡高娟, 孙丽娟, 王汝传, 等. 距离辅助的无线传感器网络节点覆盖判别模型[J]. 通信学报, 2010, 31(8): 127-133. Fan Gao-juan, Sun Li-juan, Wang Ru-chuan, et al. Distance-assistant node coverage identification model for wireless sensor networks[J]. Journal on Communications, 2010, 31(8): 127-133. [本文引用:1]
[4]	Wang X, Ma J J, Wang S. Distributed energy optimization for target trackong in wireless sensor networks[J]. IEEE Transactions on Mobile Computing, 2009, 9(1): 73-86. [本文引用:1]
[5]	Ai C, Santosh K, Ten H L. Local barrier coverage in wireless sensor networks[J]. IEEE Transactions on Mobile Computing, 2010, 10(4): 491-504. [本文引用:1]
[6]	Ma Hua-dong, Liu Yong-he. Correlation based video processing in video sensor networks[C]∥2005 International Conference on Wireless Networks, Communications and Mobile Computing, New York, USA, 2005: 987-992. [本文引用:1]
[7]	Makhoul A, Saadi R, Pham C. Coverage and adaptive scheduling algorithms for criticality management on video wireless sensor networks[C]∥The 4th ACM Int'l Workshop on Performance Monitoring, Measurement, and Evaluation of Heterogeneous Wireless and Wired Networks, St. Petersburg, 2009: 54-60. [本文引用:1]
[8]	Adriaens J, Megerian S, Potkonjak M. Optimal worst-case coverage of directional field-of-view sensor networks[C]∥Proc of the 3rd Annual IEEE Conf on Sensor, Mesh and ad hoc Communications and Network, Reston, VA, 2006: 336-345. [本文引用:1]
[9]	Ma H D, Zhang X, Ming A L. A coverage-enhancing method for 3D directional sensor networks[C]∥Proceeding of 28th IEEE Conference on Computer Communications IEEE INFOCOM 2009, Washington, 2009: 2791-2795. [本文引用:1]
[10]	肖甫, 王汝传, 孙丽娟, 等. 一种面向三维感知的无线多媒体传感器网络覆盖增强算法[J]. 电子学报, 2012, 40(1): 167-172. Xiao Fu, Wang Ru-chuan, Sun Li-juanet al. Coverage-enhancing algorithm for wireless multi-media sensor networks based on three-dimensional perception[J]. Acta Electronica Sinica, 2012, 40(1): 167-172. [本文引用:1]
[11]	Jian W, Changyong N, Ruimin S. Priority-based target coverage in directional sensor networks using a genetic algorithm[J]. Computers and Mathematics with Applications, 2009, 57(1): 1915-1922. [本文引用:1]
[12]	任秀丽, 程艳蕾, 徐泽明. 无线传感器网中三维覆盖控制和节点调度的研究[J]. 小型微型计算机系统, 2012, 33(8): 1681-1684. Ren Xiu-li, Cheng Yan-lei, Xu Ze-ming. Coverage control and node-scheduling for three-dimensional wireless sensor networks[J]. Journal of Chines Computer Systems, 2012, 33(8): 1681-1684. [本文引用:1]
[13]	Tatih T M, Bulut O, Quan P, et al. A differential evolution algorithm for median cycle problem[C]∥2011 IEEE Symposium on Differential Evolution(SDE), Paris, France, 2011: 1-7. [本文引用:1]
[14]	Herera F, Lozano M. Gradual distributed real-coded genetic algorithms[J]. IEEE Transaction on Evolutionary Computation, 2000, 4(1): 43-63. [本文引用:1]

2012

0.0

... 0 引言随着无线多媒体传感器网络(Wireless multimedia sensor networks,WMSNs)研究的深入和实际应用的扩展^[1,2,3],为增强相应覆盖控制算法的实用性和有效性^[4,5],一些学者致力于构建能够描述无线多媒体传感器节点真实感知能力的感知模型 ...

2012

0.0

2010

0.0

. 2010, 31(8):127-133

Distance-assistant node coverage identification model for wireless sensor networks

距离辅助的无线传感器网络节点覆盖判别模型

Fan Gao-juan , Sun Li-juan , Wang Ru-chuan

凡高娟, 孙丽娟, 王汝传

提出了距离辅助的节点覆盖判别模型DANCI(distance-assistant node coverage identification model),通过邻居节点到本节点的距离信息,判别该节点被邻居节点覆盖的程度.理论分析与仿真结果表明,在节点随机部署情况下,计算所得的覆盖度与节点位置已知情况下,其覆盖度的最大误差仅为6.396 0%.相对于邻居节点个数与最近邻居距离覆盖判别方法,极大提高了覆盖判别的精确性.

2009

0.0

2010

0.0

2005

0.0

... Ma等^[6]于2005年首先设计了基于节点坐标、感知半径、感知方向和感知角度的扇形感知模型,此后,Makhoul等^[7,8]先后提出三角形和凸多边形感知模型 ...

2009

0.0

... Ma等^[6]于2005年首先设计了基于节点坐标、感知半径、感知方向和感知角度的扇形感知模型,此后,Makhoul等^[7,8]先后提出三角形和凸多边形感知模型 ...

2006

0.0

... Ma等^[6]于2005年首先设计了基于节点坐标、感知半径、感知方向和感知角度的扇形感知模型,此后,Makhoul等^[7,8]先后提出三角形和凸多边形感知模型 ...

2009

0.0

... 基于此,某些研究者试图建立面向真实环境的更为准确的三维有向感知模型,如:Ma等^[9]于2009年首次提出基于传感器节点位置、主感知方向、水平方向感知范围和垂直方向感知范围的多媒体传感器节点三维感知模型 ...

2012

0.0

. 2012, 40(1):167-172 DOI:doi:10.3969/j.issn.0372-2112.2012.01.027

Coverage-enhancing algorithm for wireless multi-media sensor networks based on three-dimensional perception

一种面向三维感知的无线多媒体传感器网络覆盖增强算法

Xiao Fu , Wang Ru-chuan , Sun Li-juan

肖甫, 王汝传, 孙丽娟

Coverage is one of the hot research topics in wireless sensor networks,which indicates sensing QoS by wireless sensor networks.Motivated by the existing coverage-enhancing algorithm of wireless multimedia sensor network,a new three dimensional sensor perception model is established and a coverage-enhancing algorithm based this model (TDPCA) is proposed.This algorithm divided the three-dimensional perception model into pitch angle and deviation angle,thus the best optimal pitch angle is calculated according the location of monitoring area and nodes,and then deviation angle is optimized based on particle swarm optimization,which eliminate overlap and blind perception area effectively.Experimental results show that compared with the existing three-dimensional cover-enhancing algorithm in wireless sensor network,sensation overlap area and blind spots may be eliminated by TDPCA,and thus ultimate coverage performance of the wireless sensor network can be enhanced.

覆盖作为无线传感器网络中的基础问题直接反映了网络感知服务质量.本文在分析现有无线多媒体传感器网络覆盖增强算法的基础上,构建节点三维感知模型,提出面向三维感知的多媒体传感器网络覆盖增强算法(Three-Dimensional Perception Based Coverage-Enhancing Algorithm,TDPCA).该算法将节点主感知方向划分为仰俯角和偏向角,并根据节点自身位置及监测区域计算并调整各节点最佳仰俯角,在此基础上基于粒子群优化调整节点偏向角,从而有效减少节点感知重叠区及感知盲区,最终实现监测场景的区域覆盖增强.仿真实验表明:对比已有的覆盖增强算法,TDPCA可有效降低除节点感知重叠区和盲区,最终实现网络的高效覆盖.

2009

0.0

... 在此基础上,针对典型目标覆盖问题^[11],即求出覆盖全部目标所需的最小传感器数目,设计了一种基于仰俯角优化和偏向角优化的新型目标覆盖算法 ...

2012

0.0

. 2012, 33(8):1681-1684 DOI:doi:10.3969/j.issn.1000-1220.2012.08.010

Coverage control and node-scheduling for three-dimensional wireless sensor networks

无线传感器网中三维覆盖控制和节点调度的研究

Ren Xiu-li , Cheng Yan-lei , Xu Ze-ming.

任秀丽, 程艳蕾, 徐泽明

The coverage control of wireless sensor networks is commonly based on duality apperceiving model which makes nodes dormancy. The algorithm in practical application has limitations and is not accurate enough. In consideration of the influence of node′s perceptive ability and the path loss parameters, the three-dimensional monitoring region will be divided into a grid, and this paper proposes a sensing probability attenuation model which is based on the probability-based model. In addition, aiming at the limitations of two-dimensional cover control algorithm, this paper focuses on proposing a probability-based phrased redundant and waking-up sensor strategy. The simulation results demonstrate that this method balancesthe node′s energy, realizies the maximum effectiveness of the network energy and extends the network lifetime.

无线传感器网络中采用二元感知模型方法计算休眠冗余节点具有局限性和不精确性.本文考虑到实际应用环境对节点感知能力的影响以及传输过程中的路径损耗问题，对监测区域采用三维网格建模，并在概率感知模型的基础上提出一种概率感知衰减模型，同时对当前二维覆盖控制算法存在的各种局限性，提出了一种基于概率的分阶段冗余唤醒策略.仿真结果表明，该算法均衡了网络节点能量，实现了网络能耗的有效性，延长了网络的生存期.

... 本文受传统传感器节点的三维模型建立方式(即将二维平面内的圆节点模型旋转拓展至空间得到球形三维感知模型)的启发^[12],将多媒体传感器感知模型中应用最广的扇形模型绕节点旋转一定角度构建新型多媒体传感器三维有向感知模型,具体定义如下: ...

2011

0.0

... 差分进化算法^[13]就是该领域最具前沿、最有代表性的算法,大量实验及文献指出该方法的连续函数优化性能已超越现有较为优秀的遗传算法、粒子群算法等,为此,这里采用差分算法求解最优#cod#x003b3 ...

2000

0.0

... 这一实现方式本身就是一个组合优化的过程,对于此类问题,现在广泛采用遗传算法(Genetic algorithm,GA)进行求解,鉴于该问题与TSP问题的本质相似性,对于各种改进GA,这里选用实数编码、交换序交叉操作的遗传算法^[14]求取适应度值 ...