基于二次预测的粒子滤波算法

引用本文

武勇, 王俊, 曹运合, 张培川. 基于二次预测的粒子滤波算法. 2015, 45(5): 1696-1701
WU Yong, WANG Jun, CAO Yun-he, ZHANG Pei-chuan. Novel particle filter algorithm based on second-prediction. Journal of Jilin University Engineering and Technology Edition, 2015, 45(5): 1696-1701 复制到剪切板

Permissions

基于二次预测的粒子滤波算法

武勇, 王俊, 曹运合, 张培川

西安电子科技大学雷达信号处理国家重点实验室, 西安 710071

作者简介:武勇(1987-),男,博士研究生.研究方向:雷达信号处理,粒子滤波,并行计算.E-mail:wuyongxidian@163.com

基金:国家自然科学基金项目(61372136)

摘要

为了解决粒子滤波在粒子采样阶段没有利用观测信息的问题,提出一种基于二次预测的粒子滤波算法(SP-PF),并在图形处理器(GPU)上进行了并行实现。首先,从状态转移函数中采样得到预测粒子,通过最小二乘估计,构建一个新的粒子采样器;然后,在预测粒子的基础上,将当前的观测信息引入到粒子的二次预测中,经过两次预测后,每个新粒子都是对当前状态的无偏估计;最后,通过粒子加权的方式对当前状态进行估计,估计完成后再对粒子进行重采样。实验结果表明:该算法的估计精度优于标准粒子滤波(SPF)、辅助粒子滤波(APF)和无迹粒子滤波(UPF),且GPU显著提升了SP-PF的处理效率。

关键词: 信息处理技术; 粒子滤波; 图形处理器; 最小二乘估计

中图分类号:TN911 文献标志码:A 文章编号:1671-5497(2015)05-1696-06

Novel particle filter algorithm based on second-prediction

WU Yong, WANG Jun, CAO Yun-he, ZHANG Pei-chuan

National Laboratory of Radar Signal Processing, Xidian University, Xi'an 710071, China

Abstract

In order to handle the problem that current observation information is not used in the particle sampling stage of the Particle Filter (PF), a novel particle filter algorithm based on Second-Prediction (SP-PF) is proposed and implemented on the Graphics Processing Unit (GPU). First, sampling from the state transition function is performed to obtain the predicted particles, and by least square estimation, a new generator of sampling particles is constructed. Then, on the basis of the predicted particles, the current observation information is introduced into the secondary particle prediction. After double predictions, each new particle is an unbiased estimate of the current state. Finally, the current state is estimated by means of weighting these particles, and after the completion of state estimation, resampling is conducted. Experimental results demonstrate that the proposed algorithm improves the precision of estimation compared with Standard Particle Filter (SPF), Auxiliary Particle Filter (APF) and Unscented Particle Filter (UPF). Furthermore, the processing efficiency of SP-PF is greatly raised by using GPU.

Keyword: information processing technology; particle filter; graphics processing unit; least square estimation

Show Figures

0 引言

非线性滤波问题广泛存在于信号处理、雷达探测、目标跟踪、卫星导航等诸多领域^{[1, 2]}, 这类问题可归纳为存在观测噪声时非线性系统的状态估计问题。贝叶斯概率统计理论为这种状态估计问题提供了一套完整的数学解决方案, 其基本思想是将状态估计问题转化为后验概率密度函数或后验分布的逼近问题, 并通过递归的方式实现对状态空间的迭代估计。对于线性高斯模型来说, 传统的卡尔曼滤波被公认为是最优的贝叶斯估计, 其通过递推式更新有限维统计量来精确计算状态空间的后验分布^{[3, 4]}。然而对于大部分非线性、非高斯的情况, 状态空间后验分布的闭式解不存在或难以求解^[5], 这就需要对后验分布进行近似计算。文献[6-7]提出的粒子滤波算法是一种通用的非线性滤波算法, 其采用一系列带有权值的样本点对状态的后验概率分布进行近似, 这种算法本质上是基于状态搜索进行的。首先通过重要性密度函数随机生成若干个粒子, 每个粒子代表一个可能的状态, 然后在状态空间对它们进行传播, 使用似然函数选出最有可能生成当前观测值的若干个粒子点, 并赋予一个较大的权值, 最后通过保留下来的粒子对状态的后验分布进行近似。由于在状态逼近的过程中使用了大量的粒子, 因此该算法具有较高的计算复杂度。粒子滤波因优良的性能, 一经被提出便获得了广泛的应用^{[8, 9, 10]}。但在粒子滤波中存在着两个主要的问题:①当粒子采样不准确时, 如采样得到的粒子位于实际后验分布的拖尾区域, 经过状态搜索后, 绝大部分的粒子权值都会趋于0。这会为后验分布的近似带来很大的误差, 甚至有可能引起滤波发散。因此, 采样粒子的质量直接决定着对后验分布近似的精度。从最优重要性密度函数的表达式可以看出, 在采样粒子时, 应考虑最新的观测信息^[7]。基于此, 相继出现了辅助粒子滤波^[11]、无迹粒子滤波^{[12, 13]}、扩展卡尔曼粒子滤波^[14]以及多种卡尔曼相结合的粒子滤波^[15]等方法, 这几种方法都是将当前时刻的观测值引入到粒子的采样过程中, 以提高所选粒子的质量。②在对状态进行迭代估计过程中, 会出现粒子退化以及粒子贫化的现象^[16], 减少了状态估计中可用粒子的数量和种类, 增大了状态估计误差, 一般通过重采样技术来缓解这种现象的发生, 即在每次迭代后对粒子进行重新采样, 根据重采样的策略不同, 状态估计的精度也各不相同, 如差分演化粒子滤波及其变种^[17]。

综合以上的分析, 对粒子滤波存在问题的改进主要从如何有效利用观测信息提高采样粒子的质量和重采样策略两个方面进行。本文从第一个方面出发, 提出了一种基于二次预测的粒子滤波算法, 称为二次预测粒子滤波(SP-PF)。算法首先使用状态转移密度函数对粒子进行初采样, 获得预测粒子, 然后在预测粒子的基础上, 通过求解一个最小二乘问题, 将当前时刻的观测信息引入到粒子的二次预测中, 并使用似然函数计算新粒子的权值, 最后通过粒子加权对当前的状态进行估计, 估计完后再对粒子进行重采样。SP-PF算法的优势在于:将当前时刻的观测信息融合在粒子采样阶段, 充分利用了可信的观测信息, 避免了传统粒子滤波中观测信息仅用来评判粒子好坏的问题, 提高了位于真实后验分布附近采样粒子的数量, 缓解了迭代过程中出现的粒子退化问题, 进而改善了状态估计的精度。

1 二次预测粒子滤波算法

假设非线性系统的状态模型和观测模型分别为:

$\begin{matrix} \{\begin{matrix} x_{k} = f (x_{k - 1}) + u_{k} \\ y_{k} = h (x_{k}) + v_{k} \end{matrix} (1) \end{matrix}$

式中:x_k∈ R^m为k时刻的m维状态向量; y_k∈ Rⁿ为k时刻的n维观测向量; f(· )、h(· )为已知的函数; u_k、v_k分别为分布已知的系统噪声和观测噪声, 它们之间相互独立。

滤波的目的就是利用当前时刻的观测值和上一时刻的状态估计值, 对当前时刻的状态(后验概率密度函数)进行迭代更新。

SP-PF算法是在经典粒子滤波的框架下发展的, 通过蒙特卡洛积分的方法对状态的后验概率密度函数进行估计, 其估计的数学表达式为:

$\begin{matrix} p (x_{k} | y_{1 : k}) = \overset{N}{\sum_{i = 1}} {\bar{w}}_{k}^{i} δ (x_{k} - x_{k}^{i}) (2) \end{matrix}$

式中:N为采样的粒子数; y_1:_k为到k时刻所有观测量构成的观测序列y_1:_k={y₁, y₂, …, y_k}; $\begin{matrix} {\{x_{k}^{i}\}}_{i = 1}^{N} \end{matrix}$ 为从重要性密度函数q(x_k|x_k-₁, y_1:_k)采样得到的粒子序列; $\begin{matrix} {\bar{w}}_{k}^{i} \end{matrix}$ 为对应于每个粒子的归一化重要性权重, 满足 $\begin{matrix} \overset{N}{\sum_{i = 1}} \end{matrix} \begin{matrix} {\bar{w}}_{k}^{i} \end{matrix}$ =1。

归一化前, 粒子的重要性权重通过下式获得:

$\begin{matrix} \begin{matrix} w_{k}^{i} \approx \frac{p (y_{k} | x_{k}^{i}) p (x_{k}^{i} | x_{k - 1}^{i})}{q (x_{k}^{i} | x_{k - 1}^{i} y_{1 : k})} w_{k - 1}^{i} (3) \\ i = 1, 2, \dots, N \end{matrix} \end{matrix}$

通常选择状态转移密度函数作为重要性密度函数, 即:

$\begin{matrix} q (x_{k} | x_{k - 1}, y_{1 : k}) = p (x_{k} | x_{k - 1}) (4) \end{matrix}$

在k(k≠ 0)时刻, 首先通过重要性密度函数进行初采样, 获得预测粒子, 每个预测粒子满足:

$\begin{matrix} x_{k | k - 1}^{i} = f (x_{k - 1}^{i}) + u_{k}^{i} (5) \end{matrix}$

通过式(5)得到的预测粒子没有包含当前时刻的观测信息, 仅是对当前状态的先验估计。为了使采样粒子包含当前时刻的观测信息, 构建如下最小二乘估计问题:

$\begin{matrix} {\hat{x}}_{k} = \arg \min_{x_{k}} ‖ y_{k} - h (x_{k}) ‖_{_{2}}^{^{2}} (6) \end{matrix}$

上式是一个无约束极小化问题, 其代价函数为:

$\begin{matrix} J (x_{k}) = [y_{k} - h (x_{k} {)]}^{T} [y_{k} - h (x_{k})] (7) \end{matrix}$

式(6)所述问题可转换为代价函数求导等于0的问题, 即:

$\begin{matrix} \nabla_{x_{k}} J (x_{k}) = 0 (8) \end{matrix}$

利用状态的先验估计x_k|k-₁, 通过一阶泰勒展开式对观测函数h(x_k)进行近似, 即:

$\begin{matrix} h (x_{k}) \approx h (x_{k | k - 1}) + H_{k} (x_{k} - x_{k | k - 1}) (9) \end{matrix}$

式中:H_k= $\begin{matrix} \nabla_{x_{k}} \end{matrix}$ h(x_k) $\begin{matrix} |_{x_{k} = x_{k | k - 1}} \end{matrix}$ , 将式(9)代入J(x_k)的表达式易得:

$\begin{matrix} \begin{matrix} J (x_{k}) = [g (y_{k}, x_{k | k - 1}) - H_{k} x_{k}]^{T} \cdot \\ [g (y_{k}, x_{k | k - 1}) - H_{k} x_{k}] (10) \\ g (y_{k}, x_{k | k - 1}) = y_{k} - h (x_{k | k - 1}) + H_{k} x_{k | k - 1} \end{matrix} \end{matrix}$

对J(x_k)求导后式(8)可以转化为:

$\begin{matrix} {H^{T}}_{k} [g (y_{k}, x_{k | k - 1}) - H_{k} x_{k}] = 0 (11) \end{matrix}$

求解式(11), 经整理变形后可得当前状态x_k的最新估计为:

$\begin{matrix} {\hat{x}}_{k} = ({H^{T}}_{k} H_{k})^{- 1} {H^{T}}_{k} g (y_{k}, x_{k | k - 1}) (12) \end{matrix}$

将从式(5)采样得到的预测粒子分别代入式(12), 即可获得新的预测粒子。在新粒子中, 不仅包含了对状态的预测值(先验信息), 同时也包含了当前时刻的观测值(后验信息), 即:

$\begin{matrix} {\hat{x}}_{k}^{i} = ({H^{T}}_{k} H_{k})^{- 1} {H^{T}}_{k} [y_{k} - h (x_{k | k - 1}^{i}) + H_{k} x_{k | k - 1}^{i}] (13) \end{matrix}$

通过式(3)计算新粒子的重要性权值, 易得:

$\begin{matrix} \{\begin{matrix} w_{k}^{i} \approx p (y_{k} | {\hat{x}}_{k}^{i}) w_{k - 1}^{i} \\ w_{k - 1}^{i} = 1 / N \end{matrix} (14) \end{matrix}$

对重要性权值进行归一化处理:

$\begin{matrix} {\bar{w}}_{k}^{i} = w_{k}^{i} / \overset{N}{\sum_{i = 1}} w_{k}^{i} (15) \end{matrix}$

利用最新采样的粒子和相应的权值对当前的状态进行更新:

$\begin{matrix} {\bar{x}}_{k} = \overset{N}{\sum_{i = 1}} {\bar{w}}_{k}^{i} {\hat{x}}_{k}^{i} (16) \end{matrix}$

最后, 按文献[6]中的方法进行粒子的重采样, 重采样后各粒子的权值为1/N。

本文提出的基于二次预测的粒子滤波算法可归纳为如下步骤:

初始化:从先验概率分布p(x₀)采样得到粒子 $\begin{matrix} {\{x_{0}^{i}\}}_{i = 1}^{N} \end{matrix}$ 。

(1)根据式(4)选择重要性密度函数q(x_k|x_k-₁, y_1:_k)。

(2)根据q(x_k|x_k-₁, y_1:_k)对粒子进行初采样, 得到预测粒子 $\begin{matrix} x_{k | k - 1}^{i} \end{matrix}$ 。

(3)计算观测函数h(x_k)的雅克比矩阵H_k。

(4)根据式(13)进行二次采样, 得到包含观测信息的新粒子 $\begin{matrix} {\hat{x}}_{k}^{i} \end{matrix}$ 。

(5)根据式(14)计算粒子的重要性权值, 得到 $\begin{matrix} w_{k}^{i} \end{matrix}$ 。

(6)根据式(15)对权值进行归一化, 得到 $\begin{matrix} {\bar{w}}_{k}^{i} \end{matrix}$ 。

(7)根据式(16)对状态进行后验估计, 得到 $\begin{matrix} {\bar{x}}_{k} \end{matrix}$ 。

(8)对粒子进行重采样。

(9)k=k+1, 转到步骤(2)。

2 算法讨论

通过传统采样获得的粒子仅是对当前状态的先验估计, 这种粒子的生存能力不强, 容易出现粒子分布严重偏离真实分布的情况, 而式(12)恰好可以将观测信息和状态的先验信息有机结合在一起, 充分利用观测信息来提高采样粒子的稳健性。另外, SP-PF算法需要计算非线性观测方程的雅克比矩阵, 为状态估计过程增加了额外的运算量。由于对每个粒子的处理是相互独立的, 因此可通过并行技术(如GPU高性能并行计算)来提高算法的处理效率。

通过式(12)得到的新粒子不仅包含了当前时刻的观测信息, 而且也是当前状态的无偏估计, 证明如下:

将式(9)代入式(1)中的观测方程, 可得:

$\begin{matrix} y_{k} = H_{k} x_{k} + h (x_{k | k - 1}) - H_{k} x_{k | k - 1} + v_{k} (17) \end{matrix}$

将式(17)代入式(12), 化解易得:

$\begin{matrix} {\hat{x}}_{k} = ({H^{T}}_{k} H_{k})^{- 1} {H^{T}}_{k} (H_{k} x_{k} + v_{k}) (18) \end{matrix}$

$\begin{matrix} {\hat{x}}_{k} \end{matrix}$ 的数学期望为:

$\begin{matrix} \begin{matrix} E [{\hat{x}}_{k}] = E [({H^{T}}_{k} H_{k})^{- 1} {H^{T}}_{k} (H_{k} x_{k} + v_{k})] = \\ E [({H^{T}}_{k} H_{k})^{- 1} ({H^{T}}_{k} H_{k}) x_{k}] = \\ E (x_{k}) = x_{k} (19) \end{matrix} \end{matrix}$

式中:E[ $\begin{matrix} ({H^{T}}_{k} H_{k})^{- 1} \end{matrix} \begin{matrix} {H^{T}}_{k} \end{matrix}$ v_k]=0。

3 仿真实验

对于可信观测的非线性滤波问题, 本文所提出的SP-PF算法具有良好的状态估计精度。为了验证SP-PF算法的有效性, 本文将SP-PF与基于序贯重要性采样的标准粒子滤波(SPF)、辅助粒子滤波(APF)以及无迹粒子滤波(UPF)进行了对比。实验使用的状态方程、观测方程分别为:

x_k=1+sin(0.04π k)+0.5x_k-₁+u_k-₁(20)

$\begin{matrix} y_{k} = \{\begin{matrix} 0.2 x_{k}^{2} + v_{k}, k \leq 30 \\ 0.5 x_{k} - 2 + v_{k}, k > 30 \end{matrix} (21) \end{matrix}$

式中:系统噪声u_k服从Gamma(3, 2)分布、观测噪声v_k服从高斯分布N(0, 0.0001), 状态初值为1, 观测周期为1 s, 观测时间为50 s, 粒子数量为50。如无特别说明, 以上参数均为默认值。

实验采用均方根误差(RMSE)作为性能评价指标:

$\begin{matrix} RMSE = \sqrt[]{\frac{1}{M} \overset{M}{\sum_{m = 1}} (x_{m} - {\bar{x}}_{m})^{2}} (22) \end{matrix}$

式中:M为蒙特卡洛仿真实验次数, 默认取值为500; x_m为估计值; $\begin{matrix} {\bar{x}}_{m} \end{matrix}$ 为真值。

	Figure Option View Download New Window
	图1 不同滤波算法的状态估计结果Fig.1 State estimation results of different filters

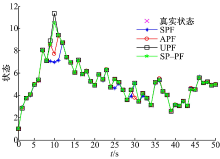
图1为一次仿真实验中4种滤波算法对状态的估计结果。从图中可以看出:UPF和SP-PF都可以很好地对状态进行逼近, 其中, SP-PF的滤波过程更加稳定, 与真值的拟合度更高。相比于UPF和SP-PF, SPF和APF的状态估计过程不够稳定, 在部分采样点上出现了轻微的滤波发散现象。在本次实验中, 从与真值的拟合度和滤波的稳定度两方面考虑, SP-PF优于其他3种算法。

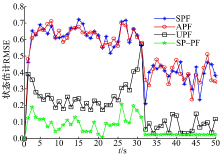
图2给出了经过500次蒙特卡洛实验后SP-PF与其他3种算法的RMSE对比图。由图可知:SP-PF的RMSE明显低于SPF、APF和UPF, 这主要是由于SP-PF的每个粒子融入了最新的观测信息, 与UPF相比, SP-PF没有对状态的后验分布作任何形式的假设。表1分别统计了图2中4种算法的单次平均运行时间、RMSE均值和标准差。RMSE的均值和标准差表征了算法的估计精度和稳定性。从表中可以清楚地看出:与SPF、APF和UPF相比, SP-PF的RMSE均值和标准差是最小的, 说明了SP-PF具有更高的估计精度和更强的稳健性。在算法的平均运行时间方面, SPF最短, SP-PF和APF次之, UPF最长。由于SP-PF需要计算观测方程的雅克比矩阵, 为状态估计过程引入了额外的运算, 因而导致其运行时间略高于SPF。APF在每次迭代中需要对粒子进行两次采样, 两次权值计算和两次重采样, 且每次的处理过程类似, 因此APF的平均运行时间约为SPF的两倍。由于UPF将无迹卡尔曼滤波器(UKF)作为粒子产生器, 每个粒子均需要通过运行UKF来产生, 因此UPF的运行效率最低。

	Figure Option View Download New Window
	图2 不同滤波算法的RMSE对比图Fig.2 Comparison of the RMSE of different filters

表1 不同滤波算法的RMSE均值、标准差和平均运行时间 Table 1 RMSE mean, RMSE standard deviation and average running time of different filters

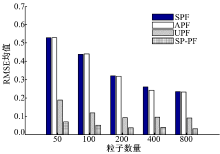
图3给出了粒子数量取不同值时, SPF、APF、UPF和SP-PF算法的RMSE均值变化情况。显然, 增加粒子数对改善算法估计精度是有益的, 随着粒子数的增加, 4种滤波算法的估计精度逐渐提高, 并趋于平稳。此外, 在粒子数量取不同值的情况下, SP-PF算法的误差均值均低于其他3种算法, 且SP-PF算法可以使用更少的粒子, 获得更高的性能, 进一步说明了该算法的性能优于其他3种滤波算法。

	Figure Option View Download New Window
	图3 粒子数量对算法性能的影响Fig.3 Effects of particle number on the performance of different filters

针对粒子滤波算法在实际应用中存在的运算量大、处理效率低的缺点, 以SP-PF算法为例, 在英伟达型号为Tesla K20的图形处理器(GPU)上对其进行了并行实现, 并与CPU的处理时间(以Matlab处理时间为代表)进行了对比, 结果如表2所示。由表2可知:GPU实现的处理时间均达到了毫秒级, 且随粒子数的增加变化缓慢, 表现出了较强的数据扩展性, 与CPU的处理时间相比, 获得了最高144倍的加速性能, 极大地提高了SP-PF算法的处理效率, 这主要得益于GPU中的上千个并行运算核。因此, GPU为实现粒子滤波算法的在线处理提供了一条有效途径。

表2 SP-PF在CPU和GPU上实现的处理时间对比 Table 2 Comparison of the processing time of the SP-PFimplemented on CPU and GPU

4 结束语

传统粒子滤波在处理非线性滤波问题时所用的粒子是通过状态转移函数从上一时刻的粒子中采样得到的, 由于在采样粒子中没有任何关于当前观测值的信息, 容易出现粒子分布严重偏离真实后验分布或粒子退化的情况, 进而影响了状态估计的精度。针对这种情况, 本文提出了一种基于二次预测的粒子滤波算法, 其基本思想是将粒子采样分为两个阶段进行。首先采样得到预测粒子, 然后通过最小二乘估计, 将观测信息用于对预测粒子的采样中, 得到包含观测信息的新的预测粒子, 最后利用这些新粒子对状态进行估计。由于在粒子采样中融入了观测量信息, 且所得到的新粒子都是对当前状态的无偏估计, 因此促进了采样粒子向高似然区域的移动, 提高了各个粒子与真实状态之间的关联性, 降低了粒子分布严重偏离真实后验分布的风险, 改善了状态估计的精度。通过计算机仿真, 将该算法与标准粒子滤波、辅助粒子滤波和无迹卡尔曼粒子滤波进行了对比, 结果显示该算法的估计精度更高、稳定性更好。由于该算法在二次预测中需要计算观测函数的雅克比矩阵, 接下来的工作可从降低算法运算量方面进行深入研究。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Sedai S, Bennamoum M, Huynh D Q. A Gausian process guided particle filter for tracking 3D human pose in video[J]. IEEE Transactions on Image Processing, 2013, 22(11): 4286-4300. [本文引用:1]
[2]	Yardim C, Gerstoft P, Hodgkiss W S. Tracking refractivity from clutter using Kalman and particle filters[J]. IEEE Transactions on Antennas and Propagation, 2008, 56(4): 1060-1069. [本文引用:1]
[3]	夏楠, 邱天爽, 李景春, 等. 一种卡尔曼滤波与粒子滤波相结合的非线性滤波算法[J]. 电子学报, 2013, 41(1): 148-152. Xia Nan, Qiu Tian-shuang, Li Jing-chun, et al. A nonlinear filter algorithm combining the Kalman filter and the particle filter[J]. Acta Electronica Sinica, 2013, 41(1): 148-152. [本文引用:1]
[4]	Kalman R E. A new approach to linear filtering and prediction problems[J]. Transactions of the AMSE Journal of Basic Engineering, 1960, 82(1): 35-45. [本文引用:1]
[5]	Kotecha J H, Djuric P M. Gaussian particle filter[J]. IEEE Transactions on Signal Processing, 2003, 51(10): 2591-2601. [本文引用:1]
[6]	Li Hong-wei, Wang Jun. Particle filter for manoeuvring target tracking via passive radar measurements with glint noise[J]. IET Radar Sonar and Navigation, 2012, 6(3): 180-189. [本文引用:1]
[7]	Arulampalam M S, Maskell S, Gordon N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 174-188. [本文引用:1]
[8]	Georgy Jacques, Korenberg Michael J, Bayoumi Mohamed M. Low-cost three-dimensional navig- ation solution for RISS/GPS integration using mixture particle filter[J]. IEEE Transactions on Vehicular Technology, 2010, 59(2): 599-614. [本文引用:1]
[9]	戴连君, 唐涛, 蔡伯根. 基于自适应粒子滤波的北斗卫星信号周跳探测[J]. 吉林大学学报: 工学版, 2013, 43(4): 1146-1152. Dai Lian-jun, Tang Tao, Cai Bo-gen. Cycle slip detection for BeiDou satellite based on adaptive particle filter[J]. Journal of Jilin University(Engineering and Technology Edition), 2013, 43(4): 1146-1152. [本文引用:1]
[10]	Wang Ya-feng, Sun Fu-chun, Zhang You-an, et al. Central difference particle filter applied to transfer alignment for SINS on missiles[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 375-387. [本文引用:1]
[11]	Pitt M K, Shephard N. Filtering via simulation: auxiliary particle filters[J]. Journal of the American Statistical Association, 1999, 94(446): 590-599. [本文引用:1]
[12]	Zhan Rong-hui, Xin Qin, Wan Jian-wei. Modified unscented particle filter for nonlinear Bayesian tracking[J]. Journal of Systems Engineering and Electronics, 2008, 19(1): 7-14. [本文引用:1]
[13]	Li Hong-wei, Wang Jun, Su Hong-tao. Improved particle filter based on differential evolution[J]. Electronics Letters, 2011, 47(19): 1078-1079. [本文引用:1]
[14]	侯静, 景占荣, 羊彦. 远距离干扰环境下目标跟踪的扩展卡尔曼粒子滤波算法[J]. 电子与信息学报, 2013, 35(7): 1587-1592. Hou Jing, Jing Zhan-rong, Yang Yan. Extended Kalman particle filter algorithm for target tracking in stand -off jammer[J]. Journal of Electronics & Information Technology, 2013, 35(7): 1587-1592. [本文引用:1]
[15]	于洪波, 王国宏, 孙芸, 等. 一种融合UKF和EKF的粒子滤波状态估计算法[J]. 系统工程与电子技术, 2013, 35(7): 1375-1379. Yu Hong-bo, Wang Guo-hong, Sun Yun, et al. Particle filtering algorithm of state estimation on fusion of UKF and EKF[J]. Systems Engineering and Electronics, 2013, 35(7): 1375-1379. [本文引用:1]
[16]	何友, 修建娟, 关欣, 等. 雷达数据处理及应用[M]. 北京: 电子工业出版社, 2013: 76-78. [本文引用:1]
[17]	李红伟, 王俊, 王海涛. 一种基于差分演化的粒子滤波算法[J]. 电子与信息学报, 2011, 33(7): 1639-1643. Li Hong-wei, Wang Jun, Wang Hai-tao. A new particle filter based on differential evolution method[J]. Journal of Electronics & Information on Technology, 2011, 33(7): 1639-1643. [本文引用:1]

2013

0.0

... 0 引言非线性滤波问题广泛存在于信号处理、雷达探测、目标跟踪、卫星导航等诸多领域^[1,2],这类问题可归纳为存在观测噪声时非线性系统的状态估计问题 ...

2008

0.0

2013

0.0

. 2013, 41(1):148-152 DOI:10.3969/j.issn.0372-2112.2013.01.026

A nonlinear filter algorithm combining the Kalman filter and the particle filter

一种卡尔曼滤波与粒子滤波相结合的非线性滤波算法

Xia Nan , Qiu Tian-shuang , Li Jing-chun

夏楠, 邱天爽, 李景春

1. Faculty of Electronic Information and Electrical Engineering, Dalian University of Technology, Dalian, Liaoning 116024, China; 2. State Radio Monitoring Center, Beijing 100037, China; 3. School of Information and Communication Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China

A nonlinear filtering algorithm is proposed based on the Kalman filter and the particle filter.The method can provide significant performance for dynamic nonlinear system which is consist of linear state equation and nonlinear measurement equation.Firstly,the particle filter is utilized for initial estimation of the state variables,and then the Kalman filter is performed.The Cramer-Rao Bound is derived for the nonlinear model.Computation complexity analysis and numerical simulations demonstrate that the proposed algorithm has the same complexity as the standard particle filter,but the estimation accuracy is higher than the standard particle filter and the extended Kalman filter.The estimation error is even lower than the Cramer-Rao Bound of the system model.

提出一种基于卡尔曼滤波与粒子滤波的非线性滤波算法.这种方法对于状态变量服从线性变化而观测方程为非线性的动态系统模型具有显著的效果.首先使用粒子滤波对状态变量进行初估计,然后对估计结果进行卡尔曼滤波,另外推导出该系统模型下状态变量估计误差的克拉美劳下界.通过计算复杂度分析及仿真实验验证,表明新方法与标准粒子滤波算法复杂度相当,但参数估计精度要高于标准粒子滤波以及扩展卡尔曼滤波算法,估计误差甚至要低于系统模型的克拉美劳下界.

... 对于线性高斯模型来说,传统的卡尔曼滤波被公认为是最优的贝叶斯估计,其通过递推式更新有限维统计量来精确计算状态空间的后验分布^[3,4] ...

1960

0.0

... 对于线性高斯模型来说,传统的卡尔曼滤波被公认为是最优的贝叶斯估计,其通过递推式更新有限维统计量来精确计算状态空间的后验分布^[3,4] ...

2003

0.0

... 然而对于大部分非线性、非高斯的情况,状态空间后验分布的闭式解不存在或难以求解^[5],这就需要对后验分布进行近似计算 ...

2012

0.0

2002

0.0

... 从最优重要性密度函数的表达式可以看出,在采样粒子时,应考虑最新的观测信息^[7] ...

2010

0.0

... 粒子滤波因优良的性能,一经被提出便获得了广泛的应用^[8,9,10] ...

2013

0.0

. 2013, 43(4):1146-1152 DOI:doi:10.7964/jdxbgxb201304048

Cycle slip detection for BeiDou satellite based on adaptive particle filter

基于自适应粒子滤波的北斗卫星信号周跳探测

Dai Lian-jun , Tang Tao , Cai Bo-gen.

戴连君, 唐涛, 蔡伯根

Before determining the carrier-phase ambiguity resolution of BeiDou satellite in precision positioning, carrier-phase cycle slips need to be detected and repaired. Due to the influences of different errors, the carrier observation equation is nonlinear and non-Gaussian, so the method of linear filtering has its limitations to detect cycle slips. In this article, nonlinear and non-Gaussian adaptive particle filtering is employed to detect cycle slips. The detection model is built by observation equation based on analyzing BeiDou cycle slip detection principle and computation process. The proposed method can meet the demand of BeiDou cycle slip detection and precision positioning using measured data. Compared with Kalman filtering method, the adaptive particle filtering cycle slip detection model is characterized by simple initialization, high accuracy and fast convergent speed.

在北斗卫星载波相位定位确定模糊度之前,载波相位数据首先需要进行周跳的探测与修复。由于误差的影响,载波观测方程具有非线性、非高斯的特性,使用一般的线性滤波法探测周跳有其局限性。本文提出利用非线性、非高斯的自适应粒子滤波探测周跳的方法。在对周跳探测原理和计算过程分析的基础上,结合北斗卫星观测方程,建立了北斗卫星相位周跳探测模型。本文方法经实测数据计算,能够满足北斗卫星周跳探测及高精度定位的需求。通过与卡尔曼滤波方法进行比较,进一步验证了自适应粒子滤波周跳探测模型具有初始化简单、精度高、收敛速度快等特点。

... 粒子滤波因优良的性能,一经被提出便获得了广泛的应用^[8,9,10] ...

2012

0.0

... 粒子滤波因优良的性能,一经被提出便获得了广泛的应用^[8,9,10] ...

1999

0.0

... 基于此,相继出现了辅助粒子滤波^[11]、无迹粒子滤波^[12,13]、扩展卡尔曼粒子滤波^[14]以及多种卡尔曼相结合的粒子滤波^[15]等方法,这几种方法都是将当前时刻的观测值引入到粒子的采样过程中,以提高所选粒子的质量 ...

2008

0.0

2011

0.0

2013

0.0

. 2013, 35(7):1587-1592 DOI:doi:doi:10.3724/SP.J.1146.2012.01476

Extended Kalman particle filter algorithm for target tracking in stand-off jammer

远距离干扰环境下目标跟踪的扩展卡尔曼粒子滤波算法

Hou Jing , Jing Zhan-rong , Yang Yan.

侯静, 景占荣, 羊彦

An Extended Kalman Particle Filter (EKPF) integrated with “negative” information (scans or dwells with no measurements) is implemented for target tracking in the Stand-Off Jammer (SOJ). In the EKPF, the Gaussian sum likelihood function which is derived from a sensor model accounting for both the positive information and negative information is directly used in the weight update of the particle filter. And the importance density function is generated by using the Extended Kalman Filter (EKF) to take full account of the current measurement, thus leading to the distribution of the particles approaching the posterior probability density function. Moreover, use of a small number of particles can achieve good tracking accuracy. Simulation results show that EKPF outperforms the EKF implementation in terms of track continuity and track accuracy but at the cost of large computation complexity.

该文在扩展卡尔曼粒子滤波算法的基础上融合了“负”信息(没有接收到观测值的扫描)来实现远距离干扰环境下的目标跟踪。在整个实现过程中，由传感器模型推导出的高斯和似然函数充分考虑了正负信息，直接用于计算粒子权重更新。并且通过扩展卡尔曼滤波算法产生重要性密度函数，利用当前时刻的量测，使得粒子的分布更接近其后验概率分布，而且使用较少的粒子个数即可达到较好的跟踪效果。仿真证明，扩展卡尔曼粒子滤波算法在航迹连续性和跟踪精度方面明显优于扩展卡尔曼滤波算法，但计算复杂度较高。

2013

0.0

. 2013, 35(7):1375-1379 DOI:doi:10.3969/j.issn.1001-506X.2013.07.04

Particle filtering algorithm of state estimation on fusion of UKF and EKF

一种融合UKF和EKF的粒子滤波状态估计算法

Yu Hong-bo , Wang Guo-hong , Sun Yun

于洪波, 王国宏, 孙芸

在扩展卡尔曼滤波算法(extended Kalman filter,EKF)和不敏卡尔曼滤波算法(unscented Kalman filter,UKF)的基础上,提出一种基于融合的粒子滤波算法(fusion based particle filter,FPF).该算法首先利用EKF与UKF分别预测粒子状态,然后通过融合算法得到粒子的重要性建议分布,实现粒子状态更新.因为充分利用了量测信息,因而能有效提高状态估计精度.仿真中通过实例将该算法与已有的粒子滤波(particle filter,PF)算法进行比较,结果表明该算法各方面性能都有较大改进.

2013

0.0

... ②在对状态进行迭代估计过程中,会出现粒子退化以及粒子贫化的现象^[16],减少了状态估计中可用粒子的数量和种类,增大了状态估计误差,一般通过重采样技术来缓解这种现象的发生,即在每次迭代后对粒子进行重新采样,根据重采样的策略不同,状态估计的精度也各不相同,如差分演化粒子滤波及其变种^[17] ...

2011

0.0

. 2011, 33(7):1639-1643

A new particle filter based on differential evolution method

一种基于差分演化的粒子滤波算法

Li Hong-wei , Wang Jun , Wang Hai-tao.

李红伟, 王俊, 王海涛