色域映射失真类型图像的质量评价

引用本文

宋超, 王瑞光, 冯英翘, 陈宇, 邓意诚. 色域映射失真类型图像的质量评价. 2015, 45(5): 1702-1708
SONG Chao, WANG Rui-guang, FENG Ying-qiao, CHEN Yu, DENG Yi-cheng. Quality assessment method for gamut mapping distortion type images. Journal of Jilin University Engineering and Technology Edition, 2015, 45(5): 1702-1708 复制到剪切板

Permissions

色域映射失真类型图像的质量评价

宋超^1,², 王瑞光¹, 冯英翘^1,², 陈宇¹, 邓意诚¹

1.中国科学院长春光学精密机械与物理研究所, 长春 130033

2.华北理工大学信息工程学院,河北唐山 063009

王瑞光(1957-),男,研究员,博士生导师.研究方向:平板显示技术,LED大屏幕显示控制系统.E-mail:wangruiguang1957@126.com

作者简介:宋超(1986-),男,博士研究生.研究方向:LED显示控制及图像处理技术.E-mail:troysung@163.com

基金:国家科技支撑计划项目(2009BAE7373B00)

摘要

针对色域映射失真类型图像,在传统算法的基础上提出了一种新的图像质量评价方法。首先,阐述了该评价方法对图像特征提取的目的及方法,并形成最终的评价公式GMSIM。然后,使用已有的3个色域映射图像集和TID2008图像库对GMSIM算法进行参数拟合和预测准确性分析,对色域映射图像库采用命中率来表征算法性能。实验结果显示:GMSIM算法对色域映射失真图像主观感知的预测准确性比传统的SSIM方法提高约4.5%,但仍有较大的进步空间;在TID2008图像库的预测性能也有所提高。

关键词: 信息处理技术; 图像质量评价; 色域映射

中图分类号:TN911 文献标志码:A 文章编号:1671-5497(2015)05-1702-07

Quality assessment method for gamut mapping distortion type images

SONG Chao^1,², WANG Rui-guang¹, FENG Ying-qiao^1,², CHEN Yu¹, DENG Yi-cheng¹

1.Changchun Institute of Optics,Fine Mechanics and Physics,Chinese Academy of Sciences, Changchun 130033,China

2.College of Information Technology,North China University of Science and Technology,Tangshan 063009,China

Abstract

For gamut mapping distortion type images, a new image assessment method was proposed based on traditional algorithms. First, each image feature extraction objective and extraction method were elaborated, and a final assessment formula, named GMSIM, was established based on these features. Then, applying three existing gamut mapping image sets and the TID2008 image library, the parameters of the GMSIM algorithm were fitted, and the prediction accuracy of the algorithm was analyzed. For gamut mapping image sets, hit rate was used as indication of the algorithm performance. Experiment results show that, compared with traditional SSIM method, the proposed GMSIM algorithm prediction accuracy of subjective perceptions for gamut mapping distortion images was improved by about 4.5%, although there is still much room for improvement. The prediction performance for TID2008 image library is also improved to some extent.

Keyword: information processing technology; image quality assessment; gamut mapping

Show Figures

目前已有的客观图像质量评价算法在预测常见图像失真类型(如有损压缩、噪声和模糊等)的主观感知方面表现出很好的准确性^[1]。黄小乔等^[2]在S-CIELAB色差模型的基础上, 提出一种基于色差的均方误差与峰值信噪比彩色图像质量评价方法, 首先将图像分别经过S-CIELAB空间滤波处理后, 再转换到CIELAB均匀颜色空间, 然后利用CIELAB色差公式计算两幅图像每一个像素间的色差, 最后计算色差均方根和色差峰值信噪比以进行质量评价。实验结果表明, 该算法的客观评价结果与平均主观评价分数具有较好的一致性。王宇庆等^[3]针对传统的图像质量评价方法忽略颜色信息的问题, 提出一种使用四元数矩阵来描述彩色图像结构信息的客观评价方法。该方法对四元数矩阵进行奇异值分解, 将最大奇异值作为度量图像结构相似性的主要参数, 并通过分析图像结构差异映射图谱得到评价结果量化值。使用LIVE图像库测试的结果表明, 该方法与人眼视觉感知特性的一致性优于传统方法。武海丽等^[4]比较了S-CIELAB和iCAM两种模型对图像质量评价结果的有效性和准确性, 分别使用两种模型计算两幅图像的色差并与主观实验结果进行对比, 发现iCAM模型色差计算结果比S-CIELAB模型更符合人眼视觉实验结果。Baranczuk等^[5]利用客观图像质量评价指标对色域映射后的图像质量进行评价, 以心理物理学主观评价结果为参照选择出最优的评价指标, 结果证明SSIM具有比主观评价结果更好的预测准确性。但上述方法均利用了图像的颜色信息, 但都没有考虑色域映射失真图像的特点, 在实验验证时也未利用色域映射图像进行验证, 对映射图像主观评价结果的预测准确性均有待验证。

本文针对色域映射失真类型图像, 在FSIM^[6]算法的基础上, 提出了一种能够提高色域映射图像预测准确性的图像质量评价方法, 可用于开发新的色域映射算法, 也可在一定程度上代替复杂费时的主观评价实验对色域映射算法的效果进行验证。

1 色域映射图像特征提取

首先将源图像和映射图像都转换到CIELAB均匀颜色空间中。对图像的明度分量, 根据人类视觉对相位一致的不同频率的波具有较高的分辨率的特性, 首先提取图像明度分量中的相位一致性信息作为图像的一个特征。由于相位一致性特征具有对比度不变性, 而视觉具有对比度敏感性, 因此提取图像明度分量中的边缘强度作为另一个特征。对图像彩度和色相分量, 根据色域映射的特点, 分别提取彩度和色相分量的彩度差和色相差作为图像的另外两个特征。

1.1 相位一致性特征提取

相位一致性(Phase congruency, PC)是一种特征点检测方法, 与传统的基于图像亮度梯度的方法不同, 它利用图像信号在特征点处的傅里叶分量具有最大相位一致性的特性来进行特征点的检测。目前已有多种提取给定图像PC图的实现方式, 本文使用Kovesi^[7]提出的一种改进的PC提取方法, 该方法已广泛应用在各种图像处理中。

为了计算二维明度图像的PC特征, 采取从一维信号到二维信号扩展的思路。首先对于一维信号g(i), 分别用 $\begin{matrix} M_{n}^{e} \end{matrix}$ 和 $\begin{matrix} M_{n}^{o} \end{matrix}$ 表示尺度为n的偶对称滤波器和奇对称滤波器, 它们是正交的。在尺度为n时, 分别使用滤波器 $\begin{matrix} M_{n}^{e} \end{matrix}$ 和 $\begin{matrix} M_{n}^{o} \end{matrix}$ 对信号进行卷积运算, 在每个像素位置i处形成一个对应的向量 $\begin{matrix} [e_{n} (i), o_{n} (i)] \end{matrix}$ = $\begin{matrix} [g (i) * M_{n}^{e}, g (i) * M_{n}^{o}] \end{matrix}$ , 可求出在像素位置i处的局部幅度为:

$\begin{matrix} A_{n} (i) = \sqrt[]{e_{n} {(i)}^{2} + o_{n} {(i)}^{2}} (1) \end{matrix}$

令F $\begin{matrix} (i) \end{matrix}$ = $\begin{matrix} \sum_{n} \end{matrix}$ e_n $\begin{matrix} (i) \end{matrix}$ , H $\begin{matrix} (i) \end{matrix}$ = $\begin{matrix} \sum_{n} \end{matrix}$ o_n $\begin{matrix} (i) \end{matrix}$ , 则一维信号的PC特征可用如下公式进行计算:

$\begin{matrix} P C_{1 D} (i) = E (i) / (ε + \sum_{n} A_{n} (i)) (2) \end{matrix}$

式中:E $\begin{matrix} (i) \end{matrix}$ = $\begin{matrix} \sqrt[]{F^{2} (i) + H^{2} (i)} \end{matrix}$ ; ε 为一个很小的常数。

对上述一维信号, 本文采用Log-Gabor滤波器组作为滤波器正交对。一维Log-Gabor滤波器在频域中的转换函数为:

$\begin{matrix} G_{1 D} (ω) = \exp \{- {[\log (ω / ω_{0})]}^{2} / (2 σ_{r}^{2})\} (3) \end{matrix}$

式中:ω ₀为滤波器的中心频率; σ _r为控制滤波器的带宽。

对上述一维Log-Gabor滤波器的垂直方向利用高斯函数作为扩展函数, 将一维Log-Gabor滤波器扩展到二维, 计算二维明度图像的PC特征。使用高斯函数作为映射函数, 得到二维Log-Gabor函数的转换函数如下:

$\begin{matrix} \begin{matrix} G_{2 D} (ω, θ_{j}) = \exp \{- {[\log (ω / ω_{0})]}^{2} / (2 σ_{r}^{2})\} \cdot \\ \exp [- {(θ - θ_{j})}^{2} / (2 σ_{θ}^{2})] (4) \end{matrix} \end{matrix}$

式中:j={0, 1, …, J-1}; θ _j=jπ /J为滤波器的方向角, J为方向数; σ _θ决定方向角的角带宽, 例如在频域中的二维Log-Gabor滤波器, ω ₀=1/6, θ _j=0, σ _θ=0.4, 如图1所示, 其中图1(a)为滤波器的径向分量, 图1(b)为滤波器的角度分量, 图1(c)为径向分量和角度分量相结合的Log-Gabor滤波器。

	Figure Option View Download New Window
	图1 频域中Log-Gabor的滤波器Fig.1 Log-Gabor filter in the frequency domain

通过调整ω ₀和θ _j的值, 并使用二维Log-Gabor滤波器G₂_D(ω , θ _j)对二维明度图像作卷积, 对每个像素位置i得到对应的向量 $\begin{matrix} [e_{n, θ_{j}} (i), o_{n, θ_{j}} (i)] \end{matrix}$ 。

在尺度为n、方向为θ _j时, 局部幅度表示为:

$\begin{matrix} A_{n, θ_{j}} (i) = \sqrt[]{e_{n, θ_{j}} {(i)}^{2} + o_{n, θ_{j}} {(i)}^{2}} (5) \end{matrix}$

沿方向θ _j的局部能表示为:

$\begin{matrix} E_{θ_{j}} (i) = \sqrt[]{F_{θ_{j}} {(i)}^{2} + H_{θ_{j}} {(i)}^{2}} (6) \end{matrix}$

式中: $\begin{matrix} F_{θ_{j}} \end{matrix} \begin{matrix} (i) \end{matrix}$ = $\begin{matrix} \sum_{n} \end{matrix} \begin{matrix} e_{n, θ_{j}} \end{matrix} \begin{matrix} (i) \end{matrix}$ ; $\begin{matrix} H_{θ_{j}} \end{matrix} \begin{matrix} (i) \end{matrix}$ = $\begin{matrix} \sum_{n} \end{matrix} \begin{matrix} o_{n, θ_{j}} \end{matrix} \begin{matrix} (i) \end{matrix}$ 。

最终可以得到二维明度图像在像素位置i处的相位一致性为:

$\begin{matrix} P C_{2 D} (i) = \frac{\sum_{j} E_{θ_{j}} (i)}{ε + \sum_{n} \sum_{j} A_{n, θ_{j}} (i)} (7) \end{matrix}$

式中:PC₂_D(i)为0到1之间的实数。

1.2 边缘强度提取

边缘是指图像中指示语义目标边界的像素集, 一般是通过寻找图像中亮度急剧变化的像素集来确定的。图像边缘包含以下两个特点:沿特定方向的局部连续性和沿正交方向的局部不连续性, 如图2(a)所示, 其中红色箭头指示沿特定方向的规则信息, 黄色箭头指示正交方向的不规则信息。本文认为, 图像中存在各向异性结构并且边缘总是向各个方向延伸^[8]。将上述3个特点全部包含在内, 构建了新的边缘强度特征提取方法。

将源图像表示为O= O¹, …, Oⁱ, …, O^N , N为图像中所有像素的个数。图像沿多个方向的局部规则性是用方向导数来测量的。

	Figure Option View Download New Window
	图2 边缘特征图和边缘强度定义Fig.2 Characteristic figure of edge and the definition of the edge-strength

用∂Oⁱ $\begin{matrix} (d) \end{matrix}$ 来表示图像第i个像素沿方向d的方向导数, 并且仅考虑4个方向, 即j=1, 2, 3, 4, 如图2(b)所示。定义垂直或者水平方向的边缘强度为:

$\begin{matrix} E S_{O}^{i} (1, 3) = {|\partial O^{i} (1) - \partial O^{i} (3)|}^{ρ} (8) \end{matrix}$

为了符合人眼视觉, 引入ρ 作为边缘强度非线性调节因子。类似地, 在对角线的边缘强度定义为:

$\begin{matrix} E S_{O}^{i} (2, 4) = {|\partial O^{i} (2) - \partial O^{i} (4)|}^{ρ} (9) \end{matrix}$

因为人眼视觉系统对显示更强边缘强度的方向更敏感, 定义第i个像素的整个边缘强度为:

$\begin{matrix} ES (O, i) = \max (E S_{O}^{i} (1, 3), E S_{O}^{i} (2, 4)) (10) \end{matrix}$

这个新定义的边缘强度把边缘的3个特征考虑在内, 并且能够使用卷积快速计算。

将源图像O的色域映射图像表示为R= R¹, …, Rⁱ, …, R^N , 为了保证源图像O和映射图像R在每个像素上能在相同的方向比较边缘强度, 定义映射图像R在第i个像素的边缘强度为:

$\begin{matrix} ES (R, i) = \{\begin{matrix} E S_{R}^{i} (1, 3), \\ E S_{R}^{i} (2, 4), \end{matrix} \begin{matrix} ES (O, i) = E S_{O}^{i} (2, 4) \\ ES (O, i) = E S_{O}^{i} (2, 4) \end{matrix} (11) \end{matrix}$

每个像素的方向导数∂ Oⁱ(d)是通过使用卷积核K $\begin{matrix} (j) \end{matrix}$ 与图像进行卷积运算得到的。卷积核的形式如下:

$\begin{matrix} \begin{matrix} K (1) = \frac{1}{16} [\begin{matrix} 0 & 0 & 0 & 0 & 0 \\ 0 & - 3 & 0 & 3 & 0 \\ 0 & - 10 & 0 & 10 & 0 \\ 0 & - 3 & 0 & 3 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{matrix}] \\ K (2) = \frac{1}{16} [\begin{matrix} 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 10 & 0 \\ - 3 & 0 & 0 & 0 & 3 \\ 0 & - 10 & 0 & 0 & 0 \\ 0 & 0 & - 3 & 0 & 0 \end{matrix}] \\ K (3) = \frac{1}{16} [\begin{matrix} 0 & 0 & 0 & 0 & 0 \\ 0 & - 3 & 10 & 3 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & - 3 & - 10 & 3 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{matrix}] \\ K (4) = \frac{1}{16} [\begin{matrix} 0 & 0 & 3 & 0 & 0 \\ 0 & 10 & 0 & 0 & 0 \\ 3 & 0 & 0 & 0 & - 3 \\ 0 & 0 & 0 & - 10 & 0 \\ 0 & 0 & - 3 & 0 & 0 \end{matrix}] \end{matrix} \end{matrix}$

卷积核的设计或选择在图像质量评价研究中十分重要, 不同的卷积核会导致不同的评价性能。在FSIM^[6]算法中, 作者对3种图像梯度卷积核(Prewitt, Sobel, Scharr)进行了比较, 结果显示Scharr算子能够达到最好的效果。本文中上述卷积核K(j)即在Scharr算子的基础上设计的。

1.3 彩度差和色相差特征提取

在大部分情况下, 色域映射过程中颜色失真是必然的。颜色三属性中, 色相是感知和辨别颜色中最主要的颜色属性。大部分色域映射算法都是以保持色相不变为原则, 并且基本上都是在CIELAB均匀颜色空间中保持色相角不变来实现, 然后在明度和彩度分量上进行颜色映射^[9]。但是, 色相角并不能完全反应视觉感知的色相, 也就是说, 即使颜色在相同色相角平面上移动, 人眼仍然会感知色相的改变, 这是由于色空间本身的不均匀性引起的。

为了表征色域映射图像与源图像的颜色分量的相似性, 分别提取源图像和映射图像在像素位置i的彩度差和色相差:

$\begin{matrix} \begin{matrix} ΔC (i) = C (O, i) - C (R, i) (12) \\ ΔH (i) = [{(a (O, i) - a (R, i))}^{2} + (b (O, i) - \\ {b (R, i))}^{2} - Δ C^{2} {(i)]}^{\frac{1}{2}} (13) \end{matrix} \end{matrix}$

式中:C(O, i)、C(R, i)分别为源图像和映射图像在像素位置i的彩度分量; a(O, i)、a(R, i)、b(O, i)、b(R, i)分别为对源图像和映射图像在CIELAB均匀颜色空间中分解对应的a和b分量。

$\begin{matrix} \begin{matrix} C (O, i) = \sqrt[]{a^{2} (O, i) + b^{2} (O, i)} (14) \\ C (R, i) = \sqrt[]{a^{2} (R, i) + b^{2} (R, i)} (15) \end{matrix} \end{matrix}$

本文中Δ H是用欧几里得距离而不是用色相角的差值来表示的, 一方面是因为在CIELAB均匀颜色空间中, 即使两种颜色的色相角的差维持不变, 随着彩度的增大, 视觉色相差也会增大。另一方面, 使用色相角的差来衡量色相变化, 不易对色相的相似性比较进行公式化。

2 色域映射失真图像质量评价

利用从图像明度分量中提取的相位一致性特征、边缘强度特征和从彩度与色相分量中提取的彩度差特征、色相差特征, 设计了一种可用于色域映射失真类型的图像质量评价方法。为方便起见, 本文将这种算法称为色域映射相似性评价算法(Gamut mapping similarity, GMSIM)。

对于图像明度分量, 从源图像O中提取的相位一致性和边缘强度特征分别为PC(O, i)和ES(O, i), 从映射图像R中提取的相位一致性和边缘强度特征分别为PC(R, i)和ES(R, i), 则源图像O和映射图像R明度分量相似性由两部分构成, 其中相位一致性特征相似性定义如下:

$\begin{matrix} S_{PC} (i) = \frac{2 PC (O, i) \cdot PC (R, i) + Q_{1}}{PC {(O, i)}^{2} + PC {(R, i)}^{2} + Q_{1}} (16) \end{matrix}$

边缘强度特征的相似性定义如下:

$\begin{matrix} S_{ES} (i) = \frac{2 ES (O, i) \cdot ES (R, i) + Q_{2}}{ES {(O, i)}^{2} + ES {(R, i)}^{2} + Q_{2}} (17) \end{matrix}$

式中:Q₁和Q₂均为正实数, 用于提高S_PC和S_ES的稳定性, 其值大小分别取决于PC和ES的动态取值范围。

$\begin{matrix} Q_{2} = {(B \times 100^{ρ})}^{2} (18) \end{matrix}$

式中:B为预先设置的常数; ρ 为边缘强度非线性调节因子。

图像中不同的像素位置在人眼视觉系统对图像视觉感知的贡献是不同的, 例如边缘位置就比平滑区域传达了更重要的视觉信息。因为人眼对相位一致性结构具有敏感性, 取源图像O和映射图像R相位一致性的最大值作为权重, 用于图像明度分量的相似性度量。图像明度分量的相似性权重定义如下:

PC_m $\begin{matrix} (i) \end{matrix}$ =max $\begin{matrix} (PC (O, i), PC (R, i)) \end{matrix}$ (19)

图像明度分量的相似性可定义如下:

$\begin{matrix} S_{L} (i) = \frac{P C_{m} (i) \cdot {[S_{PC} (i)]}^{α} \cdot {[S_{ES} (i)]}^{β}}{\sum_{i} P C_{m} (i)} (20) \end{matrix}$

式中:α 和β 是用来表示相位一致性和边缘强度特征重要性的参数。

根据源图像O和映射图像R彩度差和色相差的定义, 取在图像彩度分量和色相分量的相似性定义为:

$\begin{matrix} \begin{matrix} S_{C} (i) = \frac{1}{1 + Q_{3} \cdot Δ C^{2} (i)} (21) \\ S_{H} (i) = \frac{1}{1 + Q_{4} \cdot Δ H^{2} (i)} (22) \end{matrix} \end{matrix}$

式中:参数Q₃和Q₄用于调整所检测的彩度差和色相差大小。

将所有相似性结合在一起, 即可得到源图像O和映射图像R的相似值如下:

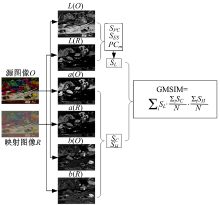
GMSIM=∑ _iS_L· $\begin{matrix} \frac{\sum_{i} S_{C}}{N} \end{matrix}$ · $\begin{matrix} \frac{\sum_{i} S_{H}}{N} \end{matrix}$ (23)

GMSIM算法在实际应用中的流程见图3。

	Figure Option View Download New Window
	图3 GMSIM算法流程图Fig.3 GMSIM algorithm scheme

3 实验结果及分析

3.1 实验图像库

本文中选用TID2008图像库^[10]作为GMSIM算法参数调试和算法性能验证的一部分图像源。TID2008数据库共有1700幅测试图像, 包括25幅源图像, 对每幅源图像各有17种失真类型, 每种失真类型有4个失真等级。数据库的主观测试值(Mean opinion scores, MOS)是由3个国家共约256 000人次实验的基础上获得的。

使用已有色域映射算法主观对比实验中形成的3个图像集^[5]作为GMSIM算法参数调试和性能验证的另一部分图像源。这几个图像集包含约15种色域映射算法及其组合, 共有234幅源图像, 2136幅色域映射图像, 共有14 106次有效主观对比评价。在图像集形成的主观对比评价实验中, 将两幅色域映射图像并排, 并将源图像置于两幅映射图像的下方, 3幅图像同时展示给观察者。观察者从两幅映射图像中选择与源图像更相似的一幅, 完成一次对比评价。

3.2 命中率

在TID2008图像库中, 最终主观评价结果是以MOS值的形式给出。客观图像质量评价算法对整个图像库进行处理, 并将运算结果与MOS值作相关性分析。相关度越高, 则客观图像质量评价算法对主观评价结果的预测性越好。

对色域映射失真类型图像而言, 将观察者对比选择原始数据转换到MOS需要假设并选择原始数据分布模型、分析观察者内和观察者间的不确定性以及分析图像内容对选择结果的影响等各种因素。因此, 本文使用命中率来衡量图像质量评价算法对色域映射图像主观对比评价结果的预测准确性。命中率p的计算式为:

$\begin{matrix} p = h / m (24) \end{matrix}$

式中:m为主观对比评价总次数; h为客观评价算法成功预测主观对比评价的次数。如果某图像质量评价算法命中率p≈ 0.5, 则表示该算法预测性能很差, 其效果近似为随机预测。

在对色域映射图像集的主观评价实验中, 不同的观察者对同样的两幅色域映射图像做出的主观评价可能是不同的。因此, 客观评价算法对主观对比评价的命中率不可能为1, 而是有一个最大值p_m。只有对同样的两幅色域映射图像做出的主观对比评价中的大多数选择做出成功预测, 客观图像质量评价算法的命中率才能达到p_m。因此, 算法的命中率存在一个取值区间即 $\begin{matrix} [0.5, p_{m}] \end{matrix}$ 。命中率越接近于p_m, 表明算法对主观评价结果的预测性能越好。鉴于p_m的存在, 本文同样以pp作为衡量客观图像质量评价算法的指标之一。

$\begin{matrix} pp = p / p_{m} (25) \end{matrix}$

3.3 参数拟合

从3个色域映射图像集中随机抽取一半源图像作为训练图像集, 用于本文图像质量评价算法的参数拟合。该训练图像集中共包括117幅源图像, 1068幅色域映射图像, 共对应7932次对比评价结果。使用该图像集对客观图像质量评价算法中的各个参数进行试错性选择, 使得算法的命中率达到最大。最终得到的参数如下:N=4, J=4, σ _r=0.5978, σ _θ=0.6545, Q₁=1.2, α =1, ρ =0.9, B=0.126, Q₂=62.75, β =0.8, Q₃=0.000 25, Q₄=0.002。Q₁、Q₂和Q₃、Q₄在各自的相似性公式中使用的方式不同, 因此不能相互比较。

3.4 色域映射图像集实验结果与分析

3个色域映射图像集的全部图像及主观对比评价结果用于测试GMSIM算法的预测准确性, 同时使用CIE推荐的色差公式Δ $\begin{matrix} E_{ab}^{*} \end{matrix}$ 、S-CIELAB图像色差公式、传统的图像质量评价算法SSIM^[11]和FSIM^[6]作为对比, 比较5种算法在该图像集上的预测准确性。

对Δ $\begin{matrix} E_{ab}^{*} \end{matrix}$ 和S-CIELAB两种色差计算方法, 分别使用以下公式计算图像色差:

$\begin{matrix} \begin{matrix} Δ E_{ab}^{*} = \frac{\sum_{i} Δ E_{ab}^{*} (i)}{N} (26) \\ S - CIELAB = \frac{\sum_{i} S - CIELAB (i)}{N} (27) \end{matrix} \end{matrix}$

式中:N为源图像中的像素个数。

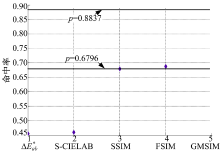
SSIM和FSIM图像质量评价算法仅使用图像的明度分量进行运算。各种图像质量评价算法得到的命中率如表1所示。

表1 图像质量评价算法命中率对比 Table 1 Comparison of hit rates

命中率	Δ $\begin{matrix} E_{ab}^{*} \end{matrix}$	S-CIELAB	SSIM	FSIM	GMSIM
p	0.4548	0.4595	0.6796	0.6874	0.7105
pp	0.515	0.520	0.769	0.778	0.804

表1 图像质量评价算法命中率对比 Table 1 Comparison of hit rates

从表1可以看出: Δ $\begin{matrix} E_{ab}^{*} \end{matrix}$ 和S-CIELAB在预测色域映射失真图像质量评价效果很差, 但比完全随机预测略好。传统的SSIM和FSIM算法的预测准确性比较高。本文提出的GMSIM算法的预测性能比SSIM和FSIM算法有了较大的提高, GMSIM算法对色域映射失真图像主观感知的预测准确性比传统的SSIM方法提高约4.5%, 但是pp值为80.4%, 表明该算法在预测色域映射失真图像的准确性方面仍有待提高, 如图4所示, 其中两条实线分别代表p_m和SSIM的命中率。

	Figure Option View Download New Window
	图4 各评价算法命中率对比Fig.4 Comparison of hit rates

3.5 TID2008图像库实验结果与分析

对SSIM、FSIM和GMSIM这3种图像质量评价算法在TID2008图像库进行了性能评估和比较, 并使用肯德尔等级相关系数(Kendall rank-order correlation coefficient, KROCC)和斯皮尔曼等级相关系数(Spearman rank-order correlation coefficient, SROCC)两种评价指标进行评价对比。等级相关系数能够测量图像质量评价方法的预测单调性, 一个更好的客观图像质量评价方法应该有更高的KROCC值和SROCC值。因为TID2008图像库为RGB数据, 首先将其从RGB颜色空间通过sRGB转换公式转换到CIELAB均匀颜色空间, 提取图像的明度图像, 然后使用3种图像质量评价算法进行处理。对GMSIM图像质量评价算法, 不使用其彩度和色相分量的相似性公式。

3种算法在TID2008图像库的预测性能对比如表2所示。从表2中可以看出:GMSIM算法优于SSIM算法和FSIM算法。因为梯度信息在只考虑图像中每个像素的平均变化, 并没有将边缘的3个特征同时考虑在内, 算法的比较结果也证明了边缘的3个特征的有用性。

表2 TID2008图像库中图像质量评价方法性能比较 Table 2 Performance comparison of IQA methods on TID2008 image database

	Figure Option View Download New Window
	图5 图像质量评价算法散点图对比Fig.5 Comparison of scatter plots

将3种算法得到的客观评价结果与TID2008图像库提供的主观评价结果绘制成散点图, 根据散点数据可得到主观观测值和各种算法的客观预测值的拟合曲线, 如图5所示。从图中可以看出:本文提出的GMSIM算法得到的散点图比SSIM和FSIM具有相对更好的聚合度, 拟合曲线线性度更好。

4 结束语

本文针对色域映射失真类型图像提出了一种新的图像质量评价方法GMSIM。使用3个色域映射图像集和TID2008图像库对GMSIM算法进行参数拟合和算法预测准确性分析。实验结果显示:GMSIM算法对色域映射失真图像主观感知的预测准确性比传统的SSIM方法提高约4.5%, 但仍有较大的进步空间。在TID2008图像库的预测性能也有所提高。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Zhang Lin, Zhang Lei, Mou Xuan-qin, et al. A comprehensive evaluation of full reference image quality assessment algorithms[C]∥IEEE International Conference on Image Processing, Orland o, 2012: 1477-1480. [本文引用:1]
[2]	黄小乔, 石俊生, 杨健, 等. 基于色差的均方误差与峰值信噪比评价彩色图像质量研究[J]. 光子学报, 2007, 36(增刊): 295-298. Huang Xiao-qiao, Shi Jun-sheng, Yang Jian, et al. Study on color image quality evaluation by MSE and PSNR based on color difference[J]. Acta Photonica Sinica, 2007, 36(Sup. ): 295-298. [本文引用:1]
[3]	王宇庆, 朱明. 评价彩色图像质量的四元数矩阵最大奇异值方法[J]. 光学精密工程, 2013, 21(2): 469-478. Wang Yu-qing, Zhu Ming. Maximum singular value method of quaternion matrix for evaluating color image quality[J]. Optics and Precision Engineering, 2013, 21(2): 469-478. [本文引用:1]
[4]	武海丽, 黄庆梅, 苑馨方, 等. 基于S-CIELAB和iCAM模型的图像颜色质量评价方法的实验研究[J]. 光学学报, 2010, 30(12): 3447-3453. Wu Hai-li, Huang Qing-mei, Yuan Xin-fang, et al. Experimental research of evaluating methods of image quality based on models of S-CIELAB and iCAM[J]. Acta Optica Sinica, 2010, 30(12): 3447-3453. [本文引用:1]
[5]	Baranczuk Z. Image-individualized gamut mapping algorithms[J]. Journal of Imaging and Technology, 2010, 54(3): 030201. [本文引用:2]
[6]	Zhang Lin, Zhang Lei, Mou Xuan-qin, et al. FSIM: a feature similarity index for image quality assessment[J]. IEEE Transactions on Image Processing, 2011, 20(8): 2378-2386. [本文引用:3]
[7]	Kovesi P. Image features from phase congruency[J]. Videre: Journal of Computer Vision Research, 1999, 1(3): 1-26. [本文引用:1]
[8]	Zhang Xuan-de, Feng Xiang-chu, Wang Wei-wei, et al. Edge strength similarity for image quality assessment[J]. IEEE Signal Processing Letters, 2013, 20(4): 319-322. [本文引用:1]
[9]	黄庆梅, 赵达尊. 彩色复制中的色域映射[J]. 照明工程学报, 2002, 13(1): 19-26. Huang Qing-mei, Zhao Da-zun. Color gamut mapping in color reproduction[J]. China Illuminating Engineering Journal, 2002, 13(1): 19-26. [本文引用:1]
[10]	Ponomarenko N, Lukin V, Zelenshy A, et al. TID2008-a database for evaluation of full-reference visual quality assessment metrics[J]. Advanced of Modern Radio-electronics, 2009, 10: 30-45. [本文引用:1]
[11]	Wang Zhou, Bovik Alan Contrad, Sheikh Hamid Rahim, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. [本文引用:1]

2012

0.0

... 目前已有的客观图像质量评价算法在预测常见图像失真类型(如有损压缩、噪声和模糊等)的主观感知方面表现出很好的准确性^[1] ...

2007

0.0

. 2007, 36(增刊):295-298

Study on color image quality evaluation by MSE and PSNR based on color difference

基于色差的均方误差与峰值信噪比评价彩色图像质量研究

Huang Xiao-qiao , Shi Jun-sheng , Yang Jian

黄小乔, 石俊生, 杨健

The performance of an image quality evaluation model can be improved by considering characteristics of the human visual system.The S-CIELAB model,which takes account of the spatial blurring by human visual system,is used to measure color difference between two color images.In this paper,it presents that the two parameters of objective evaluation of color image quality,color difference mean square error(CD-MSE) and color difference peak signal-to-noise ratio(CD-PSNR) based on the model of S-CIELAB.Objective experiments are conducted on three kinds of distorted images of JEPG2000,white Gaussian noise and transmission errors in JPEG2000 bitstream(total 180 images),compared with subjective evaluation of mean opinion score(MOS),and results show consistency between them.

在图像质量评价模型中加入人眼视觉系统特性能够提高其评价性能.彩色图像色差模型S-CIELAB是在考虑到了人眼视觉系统的空间模糊特性基础上得到两幅图像的色差，该文在S-CIELAB色差模型的基础上，提出了色差均方误差(CD-MSE)和色差峰值信噪比(CD-PSNR)彩色图像质量客观评价参量.对JEPG2000、加白噪音和图像传输中产生位错的三类失真共180幅彩色图像进行了CD-PSNR参量计算，并与国际上已经给出的主观评价结果进行了比较.实验结果表明其客观评价结果与平均主观评价分数具有较好的一致性.

... 黄小乔等^[2]在S-CIELAB色差模型的基础上,提出一种基于色差的均方误差与峰值信噪比彩色图像质量评价方法,首先将图像分别经过S-CIELAB空间滤波处理后,再转换到CIELAB均匀颜色空间,然后利用CIELAB色差公式计算两幅图像每一个像素间的色差,最后计算色差均方根和色差峰值信噪比以进行质量评价 ...

2013

0.0

. 2013, 21(2):469-478 DOI:doi:doi:10.3788/OPE.20132102.0469

Maximum singular value method of quaternion matrix for evaluating color image quality

评价彩色图像质量的四元数矩阵最大奇异值方法

Wang Yu-qing , Zhu Ming.

王宇庆, 朱明

A new color image assessment method is proposed to solve the problem of neglecting color information and a poor consistent behavior with the human visual system in traditional image quality assessment methods. The human eye sensitive image structure is enhanced and full color information is used in this method. Three important parts are taken into account in this structure, which are detail information, luminance information and color information. Quaternion is taken as a tool to perform the task. A quaternion matrix is constructed to evaluate color image quality. Then singular value decomposition is performed on the quaternion matrix. Max singular value is used to describe image structure information. Numerical results are obtained by using distortion map. 982 images in LIVE database including five types of distortion are used to investigate the behaviors of the proposed method. The nonlinearity property of the proposed method in the cross-distortion experiment is that the Root Mean Square Error(RMSE) value is 9.176,and Spearman Rank Order Correlation Coefficient(SROCC) value is 0.929 6, however, those of from Structural Similarity Index( SSIM) method are 9.299 and 0.925 6, respectively. The results show that proposed method is more consistent than the traditional methods because of the considering of more image properties and using a quaternion matrix.

针对传统的图像质量评价方法忽略颜色信息以及与人眼感知信息一致性差的问题，提出了一种全面利用彩色图像颜色信息，突出人眼敏感图像结构的彩色图像质量客观评价方法。将图像中人眼敏感的结构分为细节，亮度和颜色3方面因素，将四元数矩阵作为载体，构造了一种用于彩色图像质量评价的四元数矩阵，并对其进行奇异值分解。将最大奇异值作为度量图像结构相似性的主要参数，通过分析图像结构差异映射图谱得到了最终的量化评价结果。采用LIVE数据库中包含5种失真类型的982张测试图片验证了提出的算法，得到的交叉失真实验非线性拟合均方根误差（RMSE）值为9.176，Spearman等级相关系数（SROCC）值为0.929 6，而结构相似度（SSIM）方法的RMSE值为9.299，SROCC值为0.925 6。试验结果表明，该方法采用四元数矩阵描述彩色图像的结构信息，考虑了彩色图像的多方面结构特征，与人眼视觉感知特性的一致性优于传统方法。

... 王宇庆等^[3]针对传统的图像质量评价方法忽略颜色信息的问题,提出一种使用四元数矩阵来描述彩色图像结构信息的客观评价方法 ...

2010

0.0

. 2010, 30(12):3447-3453

Experimental research of evaluating methods of image quality based on models of S-CIELAB and iCAM

基于S-CIELAB和iCAM模型的图像颜色质量评价方法的实验研究

Wu Hai-li , Huang Qing-mei , Yuan Xin-fang

武海丽, 黄庆梅, 苑馨方

摘　要： S-CIELAB模型和iCAM模型都通过计算失真图像与原图像之间的色差对图像质量进行评价。S-CIELAB模型的空间滤波补偿了人眼视觉系统的空间混合效果。iCAM模型除了考虑空间混合效果之外,还考虑了色适应等色貌现象对图像质量评价的影响。基于视觉评价实验,选择了3幅颜色内容对比比较鲜明的图像,研究了两种模型对图像质量评价结果的有效性及准确性。研究表明,iCAM模型色差计算结果比S-CIELAB模型更符合人眼视觉实验结果。

... 武海丽等^[4]比较了S-CIELAB和iCAM两种模型对图像质量评价结果的有效性和准确性,分别使用两种模型计算两幅图像的色差并与主观实验结果进行对比,发现iCAM模型色差计算结果比S-CIELAB模型更符合人眼视觉实验结果 ...

2010

0.0

... Baranczuk等^[5]利用客观图像质量评价指标对色域映射后的图像质量进行评价,以心理物理学主观评价结果为参照选择出最优的评价指标,结果证明SSIM具有比主观评价结果更好的预测准确性 ...

... 使用已有色域映射算法主观对比实验中形成的3个图像集^[5]作为GMSIM算法参数调试和性能验证的另一部分图像源 ...

2011

0.0

... 本文针对色域映射失真类型图像,在FSIM^[6]算法的基础上,提出了一种能够提高色域映射图像预测准确性的图像质量评价方法,可用于开发新的色域映射算法,也可在一定程度上代替复杂费时的主观评价实验对色域映射算法的效果进行验证 ...

... 在FSIM^[6]算法中,作者对3种图像梯度卷积核(Prewitt,Sobel,Scharr)进行了比较,结果显示Scharr算子能够达到最好的效果 ...

... 、S-CIELAB图像色差公式、传统的图像质量评价算法SSIM^[11]和FSIM^[6]作为对比,比较5种算法在该图像集上的预测准确性 ...

1999

0.0

... 目前已有多种提取给定图像PC图的实现方式,本文使用Kovesi^[7]提出的一种改进的PC提取方法,该方法已广泛应用在各种图像处理中 ...

2013

0.0

... 本文认为,图像中存在各向异性结构并且边缘总是向各个方向延伸^[8] ...

2002

0.0

. 2002, 13(1):19-26 DOI:doi:10.3969/j.issn.1004-440X.2002.01.005

Color gamut mapping in color reproduction

彩色复制中的色域映射

Huang Qing-mei , Zhao Da-zun.

黄庆梅, 赵达尊

由于各种颜色设备能表现的颜色范围,即色域各不相同,用一个设备复制另一个设备的颜色时,可能无法原样再现.为了尽可能减少这种颜色失真,在复制前需进行设备间的色域映射操作.本文举例介绍了当前颜色复制系统中的色域映射技术和算法,分析比较了各种方法及色域映射中的相关问题.

... 大部分色域映射算法都是以保持色相不变为原则,并且基本上都是在CIELAB均匀颜色空间中保持色相角不变来实现,然后在明度和彩度分量上进行颜色映射^[9] ...

2009

0.0

... 1 实验图像库本文中选用TID2008图像库^[10]作为GMSIM算法参数调试和算法性能验证的一部分图像源 ...

2004

0.0

... 、S-CIELAB图像色差公式、传统的图像质量评价算法SSIM^[11]和FSIM^[6]作为对比,比较5种算法在该图像集上的预测准确性 ...