非均匀噪声下基于BOOTSTRAP和特征空间投影的信源数估计

引用本文

郭立民, 冯凯. 非均匀噪声下基于BOOTSTRAP和特征空间投影的信源数估计. 2015, 45(5): 1724-1730
GUO Li-min, FENG Kai. Source detection based on characteristic subspace projection and Bootstrap technique in nonuniform noise. Journal of Jilin University Engineering and Technology Edition, 2015, 45(5): 1724-1730 复制到剪切板

Permissions

非均匀噪声下基于BOOTSTRAP和特征空间投影的信源数估计

郭立民, 冯凯

哈尔滨工程大学信息与通信工程学院,哈尔滨 150001

作者简介:郭立民(1977-),男,副教授.研究方向:宽带信号处理、检测与识别.E-mail:guolimin@hrbeu.edu.cn

基金:国家自然科学基金项目(61202410)

摘要

针对阵列系统接收数据有限且存在空间非均匀噪声的信源数估计问题,提出一种基于Bootstrap和特征子空间投影的新方法。该方法将阵列信号的协方差矩阵分别投影到信号的特征子空间和噪声的特征子空间,提出了以特征空间投影为基础的一系列假设检验。数据分布未知,应用Bootstrap技术估计零假设下检测统计量的分布。通过仿真证明了所提方法在信源等功率、不等功率以及噪声功率不等的情况下有较好的性能,尤其在低信噪比和小快拍数的情况下有较好的性能。

关键词: 信息处理技术; 信源数检测; Bootstrap; 特征空间投影; 假设检验

中图分类号:TN911.23 文献标志码:A 文章编号:1671-5497(2015)05-1724-07

Source detection based on characteristic subspace projection and Bootstrap technique in nonuniform noise

GUO Li-min, FENG Kai

College of Information and Telecommunication, Harbin Engineering University, Harbin, 150001, China

Abstract

Considering the problem of source number estimation in the presence of unknown spatially nonumiform noise and the limitation of the received data, a now method based on Bootstrap technique and characteristic subspace projection is proposed. The estimation projects covariance matrix estimate of array signal into signal eigen subspace and noise eigen subspace respectively. A sequential hypothesis test is formulated based on characteristic subspace projection. No assumption is made in the distribution of the data and the Bootstrap is used to estimate the distribution under the null of the proposed test statistics. Simulation results show that the proposed method has good performances when the signal power is equal or different and under the condition of space-nonuniform noise environment, especially in the low signal-to-noise ratio and small snapshots.

Keyword: information processing technology; source detection; bootstrap technique; characteristic subspace projection; hypothesis

Show Figures

0 引言

阵列信号处理在许多应用领域有着重要作用。信源数检测作为信号参数估计的先决条件, 是阵列信号处理中至关重要的问题^{[1, 2]}。最早的信源数检测问题是采用假设检验, 需要人为地设置门限^[3], 因而人们提出了预先设定包含门限置信区间的检测方法^[4]。经典的信源数检测方法以AIC和MDL信息论准则为基础^[5], AIC准则缺乏一致性, MDL准则是一致估计, 但在低信噪比和小快拍数的情况下不能保证检测性能。在文献[6, 7]中对MDL准则做出一些修改来提高其检测性能。近年来, 为了适应更加真实的信号环境, 提出了许多新方法:文献[8]使用了观测值的概率密度函数, 在信息论准则的框架下从样本协方差矩阵获得样本特征值, 其缺点是在实际阵列系统中数据分布往往是未知的。一般的信源数检测方法都假设噪声为空间均匀的, 噪声的均匀性能够完全利用数据协方差矩阵的特征值所包含的信息, 然后实际的阵列噪声往往是空间非均匀的, 即各传感器信道噪声不一致时, 使得大部分的算法失效。在文献[9]中提到了空间非均匀噪声下信源数检测问题的模型。盖氏圆方法^{[10, 11, 12]}能够适用于空间非均匀噪声的环境, 但其在信噪比较低时常常会产生欠估计或过估计, 且需要对(M-1)× (M-1)阶的矩阵特征值分解, 而在波达方向估计中需要M× M阶特征值分解, 因此在获得波达方向是需要做两次矩阵特征值分解, 运算量过大。

在许多实际的系统中, 高斯数据和大样本数量的假设是无法满足的^[13], 所以本文提出了一种基于假设检验的替代方法。提出的假设检验以特征空间投影为基础。零假设下的检验统计量的分布是使用Bootstrap方法来估计的^{[14, 15]}, 这种方法对高斯分布和大部分非高斯分布都是有效的, 且其优点是估计在确定样本数量下的经验分布, 而不是渐进分布。因此, 提出新方法的优点是可以解决不满足高斯分布和渐进分布条件下的问题。仿真结果表明, 所提出的方法在少的样本数量和低信噪比下, 有较好的估计性能。

1 数据模型

设N个远场窄带信号入射到由M个阵元组成的均匀线阵, 入射角为θ ₁, …, θ _N, 阵元间距为d=λ /2。信源数N为未知估计量, 则线阵接收的阵列信号为^[9]:

$\begin{matrix} X (t) = AS (t) + N (t) (1) \end{matrix}$

式中:X $\begin{matrix} (t) \end{matrix}$ , S $\begin{matrix} (t) \end{matrix}$ 和N $\begin{matrix} (t) \end{matrix}$ 为均值为零的随机过程, A= $\begin{matrix} [a (θ_{1}), \dots, a (θ_{N})] \end{matrix}$ 为阵列导向矩阵, S $\begin{matrix} (t) \end{matrix}$ 是信号矢量, N $\begin{matrix} (t) \end{matrix}$ 是噪声矢量。

加性噪声假设为零均值的空间非均匀白噪声, 其协方差矩阵满足下式:

$\begin{matrix} Q = E [N (t) N^{H} (t)] = diag (q) (2) \end{matrix}$

这里 $\begin{matrix} {(\cdot)}^{H} \end{matrix}$ 为矩阵的共轭转置算子, 空间非均匀噪声各传感器能量各不相同, q= $\begin{matrix} {[σ_{1}^{2}, \dots, σ_{M}^{2}]}^{Τ} \end{matrix}$ 。信号和噪声假设是不相关的, 且各自分布未知。阵列协方差矩阵为:

$\begin{matrix} R = E [X (t) X^{Η} (t)] = A R_{S} A + Q (3) \end{matrix}$

式中:R_S=E $\begin{matrix} [S (t) S^{Η} (t)] \end{matrix}$ 是信号协方差矩阵。接收信号假设为零均值高斯过程^[9]。

2 信源数检验

2.1 非均匀噪声下的MDL准则

由于传感器噪声能量各不相同, 令阵列的任意元素失效来减轻各传感器噪声的作用。简单而不失一般性, 第M个传感器失效, 协方差矩阵进行分块:

$\begin{matrix} R = [\begin{matrix} R_{M} & r \\ r^{Η} & r_{MM} \end{matrix}] (4) \end{matrix}$

取M-1维方差的特征空间(即特征矩阵E, 满足EE^Η=I且R_M=EΣ 'E^Η)构成酉变化矩阵^[11]:

$\begin{matrix} T = [\begin{matrix} E & 0 \\ 0^{Η} & 1 \end{matrix}] (5) \end{matrix}$

这样酉变化之后的矩阵为:

$\begin{matrix} R_{T} = T^{Η} RT = [\begin{matrix} E^{Η} R_{M} E & E^{Η} r \\ r^{Η} E & r_{MM} \end{matrix}] = [\begin{matrix} Σ' & c \\ c^{Η} & r_{MM} \end{matrix}] (6) \end{matrix}$

矢量c的元素c_m幅度值ρ _m= $\begin{matrix} |c_{m}| \end{matrix}$ 是盖氏圆半径^[11], 其指出了特征值多样性和特征矢量对应空间^[16]:

$\begin{matrix} ρ_{1} \geq ρ_{2} \geq \dots \geq ρ_{N} \geq ρ_{N + 1} = \dots = ρ_{M - 1} = 0 (7) \end{matrix}$

从上式可以清楚地看出, 两个不同的圆盘, 前N个半径ρ ₁…ρ _N代表了信号子空间, 最小的M-1-N半径代表了噪声子空间。

当噪声为空间非均匀的情况下, 不能通过协方差矩阵的特征值排序来进行信号源检测, 我们用ρ _m= $\begin{matrix} |c_{m}| \end{matrix}$ 所包含的信息来代替。容易得到观测数据的负对数似然方程为^[17]:

$\begin{matrix} Λ (η) = Lln \{\det [R (η)]\} + trace \{R^{- 1} (η) \hat{R}\} (8) \end{matrix}$

这里η 是参数, $\begin{matrix} \hat{R} \end{matrix}$ 是样本协方差矩阵:

$\begin{matrix} \hat{R} = \frac{1}{L} \overset{L}{\sum_{t = 1}} X (t) X^{Η} (t) (9) \end{matrix}$

式(5)定义的酉矩阵TT^Η=I, 我们可以用协方差变换矩阵R_T代替式(8)中的R, 省略独立于N的部分, 最终我们推导得出的负对数似然函数变为:

$\begin{matrix} Λ (N) = Lln (r_{MM} - \overset{N}{\sum_{m = 1}} \frac{{|ρ_{m}|}^{2}}{λ'_{m}}) (10) \end{matrix}$

根据文献[5], 罚函数可以用来进行信息论准则的信源数检测。一般, MDL准则可以表达如下:

$\begin{matrix} NU - MD L_{M} (N) = Λ (N) + P (N) (11) \end{matrix}$

MDL准则的罚函数被定义为:

$\begin{matrix} P (N) = \frac{1}{2} (N + N^{2}) \ln \{L\} (12) \end{matrix}$

2.2 基于盖世圆半径的假设检验

使用样本协方差矩阵 $\begin{matrix} \hat{R} \end{matrix}$ 和盖氏圆半径 $\begin{matrix} {\hat{ρ}}_{m} \end{matrix}$ , 通过同时检验对应于噪声空间的盖氏圆半径 $\begin{matrix} {\hat{ρ}}_{m} \end{matrix}$ , 可以推导出被估计的信源数N。这里我们称这种方法为GBootstrap。使用如下统计检测量^{[18, 19]}:

T₁_i= $\begin{matrix} \overset{M - 1}{\sum_{m = i + 1}} \end{matrix}$ m², i=0, 1, 2, …, M-2 (13a)

T₂_i= $\begin{matrix} (\frac{1}{M - 1 - i} \overset{M - 1}{\sum_{m = i + 1}} m) \end{matrix}$ - $\begin{matrix} {(\overset{M - 1}{\prod_{m = i + 1}} {\hat{ρ}}_{m})}^{\frac{1}{M - 1 - i}} \end{matrix}$ (13b)

在实际中, 如果所有的盖氏圆半径都对应于噪声空间, 统计量T₁_i(半径平方累计和)和T₂_i(算术均值和几何均值的差异)将非常小(接近于0), 否则会比零值大很多。根据这种变化, 进行以下一系列独立的假设检验^[19]:

$\begin{matrix} \{\begin{matrix} H_{0} & : & ρ_{1} & = & \dots & = & ρ_{M - 1} \\ ⋮ & ⋮ \\ H_{i} & : & ρ_{i + 1} & = & \dots & = & ρ_{M - 1} \\ ⋮ & ⋮ \\ H_{M - 2} & : & = & \dots & = & ρ_{M - 1} \end{matrix} \begin{matrix} = & 0 \\ ⋮ \\ = & 0 \\ ⋮ \\ = & 0 \end{matrix} (14) \end{matrix}$

检测从H₀开始, 当接收H₀时意味着没有信号源存在, 信号源数目为N=0。如果H₀被拒绝, 那么相对的K₀:( $\begin{matrix} {\hat{ρ}}_{0} \end{matrix}$ ≠ 0or …or $\begin{matrix} {\hat{ρ}}_{M - 1} \end{matrix}$ ≠ 0)被接受, 意味着至少存在一个信号, 然而没有信息能够说明具体存在几个信号。因此, 通过逐步进行假设Η _i, 最大的盖氏圆半径的作用被减小。当某一假设被接受或者到达H_M-₂时, 检验停止。

对于给定的显著水平α , 其含义为当前没有信号存在时, 正确检测数信号源数目N=0的概率被维持在1-α 。因此, 每个假设都在显著水平α 下被检验。

2.3 提出的新方法

我们知道R的M-N个最小的特征值是噪声方差的估计值, 为了减小噪声的贡献, 执行降噪运算, 取R_X=R-γ ²I, 其中γ ²为阵列信号样本协方差矩阵最小的两个特征值的平均值, 即γ ²= $\begin{matrix} (σ_{M - 1}^{2} - σ_{M}^{2}) \end{matrix}$ /2。

由式(3)得出:

$\begin{matrix} R = [A R_{S} {b^{Η}}_{1}, \dots, A R_{S} {b^{Η}}_{M}] + Q (15) \end{matrix}$

式中:b_i是A的行矢量, 阵列协方差矩阵可表示为:

$\begin{matrix} R = U_{C} Σ {U^{Η}}_{C} (16) \end{matrix}$

式中:Σ 和U_C分别为阵列信号协方差矩阵特征值组成的对角矩阵和特征矢量矩阵。可以证明, 经过降噪处理的阵列信号协方差矩阵为:

$\begin{matrix} R_{X} = U_{C} Σ' {U^{Η}}_{C} = U_{S} Σ'_{S} {U^{Η}}_{S} + U_{N} Σ'_{N} {U^{Η}}_{N} (17) \end{matrix}$

式中:Σ '为阵列信号的特征值减去噪声功率估计γ ²后组成的对角阵; U_C与降噪前相同, U_C可以表示为U_C= $\begin{matrix} [u_{1}, \dots, u_{M}] \end{matrix}$ , 其中u_i是R_X的特征矢量, R_X的特征值从大到小排列, u_i按与其对应的特征值的大小排列, 求R_X在U_C上的投影 $\begin{matrix} {U^{Η}}_{C} \end{matrix}$ R_X, 其i列为:

$\begin{matrix} \begin{matrix} P_{i} = {[p_{1 i}, \dots, p_{Mi}]}^{Τ} (18) \\ P = [P_{1}, \dots, P_{M}] = \end{matrix} \end{matrix}$

$\begin{matrix} {[{U^{Η}}_{C} A R_{S} {b^{Η}}_{1}, \dots, {U^{Η}}_{C} A R_{S} {b^{Η}}_{M}]}^{Τ} \end{matrix}$ +Q-γ ²I(19)

由于信号特征子空间与导向矢量在同一空间内, 对应的投影的模 $\begin{matrix} |p_{mi}| \end{matrix}$ 应该是一个相对较大的值。由于噪声特征子空间与导向矢量正交, 对应的投影p_mi的模在理论上为零, 而实际上常常是相对较小的值。

各信号的功率常常是不等的, 为了提高估计性能, 对信号功率进行归一化以消除各个信号功率不同对信源数估计产生的影响。投影还可以表示为:

$\begin{matrix} \begin{matrix} {U^{Η}}_{C} R_{X} = {[U_{S} U_{N}]}^{Η} [U_{S} Σ'_{S} {U^{Η}}_{S} + U_{N} Σ'_{N} {U^{Η}}_{N}] = \\ [\begin{matrix} Σ'_{S} {U^{Η}}_{S} \\ Σ'_{N} {U^{Η}}_{N} \end{matrix}] (20) \end{matrix} \end{matrix}$

由上式, 功率归一化后, R_X在U_C上的投影就是 $\begin{matrix} {U^{Η}}_{C} \end{matrix}$ , 因此我们可以用U_C估计目标数。u_i表示为:u_i= $\begin{matrix} {[u_{1 i}, \dots, u_{Mi}]}^{Τ} \end{matrix}$ 。 $\begin{matrix} {U^{Η}}_{C} \end{matrix}$ 第m行元素模的均值为:

$\begin{matrix} \bar{|u_{m}|} = \frac{1}{M} \overset{M}{\sum_{i = 1}} |u_{mi}| (21) \end{matrix}$

基于上面的分析 $\begin{matrix} \bar{|u_{m}|} \end{matrix}$ 分为大小两组, 大的一组对应于信源, 因此, 基于其所包含的信息, 可以分离出信号和噪声空间。与式(13)相似, 我们使用如下的统计量:

$\begin{matrix} \begin{matrix} T_{1 i} = \overset{M}{\sum_{m = i + 1}} {\bar{|u_{m}|}}_{,}^{2} i = 0, 1, 2, \dots, M - 1 (22 a) \\ T_{2 i} = (\frac{1}{M - i} \overset{M}{\sum_{m = i + 1}} \bar{|u_{m}|}) - {(\overset{M}{\prod_{m = i + 1}} \bar{|u_{m}|})}^{\frac{1}{M - i}} (22 b) \end{matrix} \end{matrix}$

如果特征矢量对应于噪声空间, 则检测统计量T₁_i和T₂_i接近于零。进行下面的一系列独立的假设检验。实际估计信源数从Η ₀开始, 当前假设被拒绝时进行下一个假设, 直到接受为止。

$\begin{matrix} \{\begin{matrix} Η_{0} & : & \bar{|u_{1}|} & = & \dots & = & \bar{|u_{M}|} \\ ⋮ & ⋮ \\ Η_{i} & : & \bar{|u_{i + 1}|} & = & \dots & = & \bar{|u_{M}|} \\ ⋮ & ⋮ \\ H_{M - 1} & : & = & \dots & = & \bar{|u_{M}|} \end{matrix} \begin{matrix} = & 0 \\ ⋮ \\ = & 0 \\ ⋮ \\ = & 0 \end{matrix} (23) \end{matrix}$

这里显著水平与式(14)的假设检验的显著水平α 相同, 表示当前没有信号存在时, 正确检验出N=0的概率被维持在1-α 。

2.4 Bootstrap对于分布的估计

进行假设检验的显著度估计需要检验统计量的空域分布知识, Bootstrap方法用来进行零假设下的非参数估计^[18]。使用Bootstrap方法可以避免对数据分布做出假设。如前文提到的, 这个优点是非常重要的。Bootstrap方法的原理是数据样本代表了真实分布的经验估计。因此用Bootstrap方法重新采样的数据集进行推理。Bootstrap方法避免了小样本情况下的渐进估计的错误。类似地, 文献[20]强调了改善复杂的检验统计量的经验分布的估计问题, 例如对更少的样本进行重采样。

第b个Bootstrap方法重采样样本为 $\begin{matrix} X_{b}^{*} \end{matrix} \begin{matrix} (t) \end{matrix}$ , 且b=1, …, B, t=1, …, L。通过B次Bootstrap方法重新采样, 文献[20-21]给出了空域下的检验统计量的经验分布估计为:

$\begin{matrix} i^{Η} (b) = T_{i}^{*} (b) - T_{i}, b = 1, \dots, B (24) \end{matrix}$

这里T_i为从数据X $\begin{matrix} (t) \end{matrix}$ 得到的检验统计量, $\begin{matrix} T_{i}^{*} \end{matrix}$ 为从重采样样本 $\begin{matrix} X_{b}^{*} \end{matrix} \begin{matrix} (t) \end{matrix}$ 得到的检验统计量。

文献[20, 21]给出假设检验的显著度定义如下:

$\begin{matrix} P_{i} = \frac{1}{B} \overset{B}{\sum_{1}} I (|T_{i}| \leq |i^{Η} (b)|) (25) \end{matrix}$

这里I $\begin{matrix} (\cdot) \end{matrix}$ 为指标函数。因此, 检验量为α , 从i=0开始, 如果P_i≥ α , 那么Η _i被接受, 否则, 设i=i+1并且重复检验。

3 仿真结果

线性均匀阵列阵元数目为M=5, 真实信源数为N=2, 快拍数为L=100, 重采样次数B=100, 检验量α =2%信号波达方向为θ = $\begin{matrix} {[4 °, 20 °]}^{Τ} \end{matrix}$ , 信噪比SNR=10 dB, 且最差噪声比WNPR=10。

这里SNR和WNPR定义如下:

$\begin{matrix} \{\begin{matrix} SNR = 10 \lg (P_{s} / P_{n}) \\ WNPR = σ_{\max}^{2} / σ_{\min}^{2} \end{matrix} \end{matrix}$

蒙特卡洛实验次数为1000, 除了特殊说明, 假设信号和噪声为高斯分布。

图1为检测器性能与信噪比的关系对比图。信噪比从-15 dB变化到20 dB, 快拍数为100, 可以看出, 检测器性能随着信噪比的增大而提高。在非均匀噪声的情况下, AIC和MDL信息论准则失效。在低信噪比下, 所提方法的性能优于GBootstrap算法和NU-MDL算法, 同时在高信噪比下, 新方法的检测器性能略好。基于Bootstrap方法的检测器因不需要任何数据分布的先验知识而表现优异。

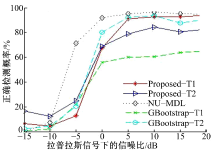
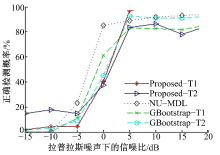
	Figure Option View Download New Window
	图1 在非均匀噪声下改变信噪比的检测器性能Fig.1 Probability of detection against SNR

图2为拉普拉斯信号和高斯噪声, 图3为高斯信号和拉普拉斯噪声, 可以看出, 当信号或者噪声不满足高斯分布时, NU-MDL的性能并没有在高斯分布的情况下表现出来。基于Bootstrap方法的检测器不需要对数据分布做出假设, 当信噪比增加时, 性能优于NU-MDL。新算法因对阵列协方差矩阵降噪处理, 应用信号子空间和噪声子空间的正交性, 易于表征投影的大小区分信号和噪声的贡献, 所以性能优于GBootstrap算法。新算法的检测性能同高斯分布的情况下基本相同, 说明了检测器的鲁棒性较好。

	Figure Option View Download New Window
	图2 在拉普拉斯信号下改变信噪比的检测器性能Fig.2 Probability of detection with Laplacian signals

	Figure Option View Download New Window
	图3 在拉普拉斯噪声下改变信噪比的检测器性能Fig.3 Probability of detection with Laplacian noise

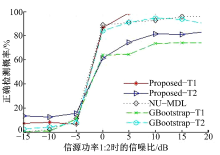
图4为信源功率不相等的情况下, 检测概率随信噪比的变化。两个信号的功率比为1∶ 2, 信噪比以最小信号功率为基准, 由图可见, 在信源功率不相等的情况下, 新方法依然好于其他两种方法。

	Figure Option View Download New Window
	图4 信源功率不等情况下改变信噪比的检测器性能Fig.4 Probability of detection with signal’ s power different

图5说明了快拍数对检测器性能的作用。与预期的一样, 在快拍数变化时, 基于Bootstrap方法的检测器性能随着快拍数增加而提高, 当快拍数达到60时, 正确检测概率不再变化, 趋于稳定。

	Figure Option View Download New Window
	图5 改变快拍数的检测器性能Fig.5 Probability of detection against sample size

	Figure Option View Download New Window
	图6 改变WNPR时的检测器性能Fig.6 Probability of detection against WNPR

图6说明当WNPR变化时的检测性能。这里假设最小噪声功率为0.1, 最大的噪声功率为0.1× WNPR, 其他噪声功率在最小噪声功率和最大噪声功率之间随机取值。令WNPR的值从1变化到45。注意到WNPR接近1, 此时最大噪声功率和最小噪声功率相等, 相当于噪声为空间均匀的, 所以检测概率最高。从图中可以看出NU-MDL和GBootstrap方法检测器T₁对非均匀噪声的敏感性。这里为高斯数据, 所提出的新检验方法性能优于NU-MDL算法和GBootstrap算法, 当WNPR小于15时, 检测器T₁的检测概率接近于100%, 当WNPR大于20时, 新方法的正确检测概率不会随着WNPR的变化而变化。

图7说明了信号角度分辨率对检测性能的影响。这里令θ ₁=10° , 并且θ ₂设置为从10° 逐渐变化到26° 。检测性能随着角度分辨率的增加而提高, 注意到, 角度分辨率大于6° 时, 用所提出的方法的检测器T₁是一致估计。

	Figure Option View Download New Window
	图7 改变角度分辨率的检测器性能Fig.7 Probability of detection against the angular resolution

图8说明阵元数目M和快拍数L对检测器T₁性能的联合作用。快拍数从20变化到120, 通过不同的阵元数目来衡量其性能。一般来说, 检测器的性能随着L增加而得到改善。另一个重要的观测结果是M的作用, 实际上, 随着X(t)维度的增加, Bootstrap需要更大的“ 最小” 快拍数来估计不同变量的经验分布。因此, 在L≤ 70, M=8的检测概率要小于M=6。另一方面, 在某一个数值(比如L=80), Bootstrap可给出更好的结果, 当增加M和L, 其联合作用明显地改善了检测器的检测概率。

	Figure Option View Download New Window
	图8 阵元和快拍数的关系以及检测器T₁的性能Fig.8 Relation between M and L and effect on the T₁ detector’ s performance.

4 结束语

文章提出了一种在空间非均匀噪声下的信号检测模型。这种模型基于信号空间和噪声空间的正交性, 提出了一系列假设检验, 并且数据分布的先验知识未知。所提出的检验统计量是基于特征空间的投影, 其在空域下的分布用Bootstrap方法进行估计。仿真结果表明, 所提出的方法在少量样本的情况下, 性能优于其他算法, 尤其当数据为非高斯数据, 或者在低信噪比等不理想的条件下。当重采样次数B增加时, 计算量增大, 然而仍在计算机可处理的能力范围内。因此, 提出的检测模型在信源数估计问题中, 性能优于其他算法。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Zoubir A M. Bootstrap methods for model selection[J]. International Journal of Electronics and Communications, 1999, 53(6): 386-392. [本文引用:1]
[2]	Zoubir A M, Iskand er D R. Bootstrap Techniques for Signal Processing[M]. Cambridge: Cambridge University Press, 2004. [本文引用:1]
[3]	Lawley D. Tests of significance for the latent roots of covariance and correlation matrices[J]. Biometrika, 1956, 43: 128-136. [本文引用:1]
[4]	Chen W, Wong K M, Reilly J P. Detection of the number of signals: a predicted eigen-threshold approach[J]. IEEE Trans on Signal Processing, 1991, 39(5): 1088-1098. [本文引用:1]
[5]	Wax M, Kailath T. Detection of signals by information theoretic criteria[J]. IEEE Transactions Acoustics Speech Signal Processing, 1985, 33(2): 387-392. [本文引用:1]
[6]	Fishler E, Messer H. Order statistics approach for determining the number of sources using an array of sensors[J]. IEEE Signal Processing Letter, 1999, 6: 179-182. [本文引用:1]
[7]	Huang L, So H C. Source enumeration via MDL criterion based on linear shrinkage estimation of noise subspace covariance matrix[J]. IEEE Transactions on Signal Processing, 2013, 61(19): 4806-4821. [本文引用:1]
[8]	Lu Z H, Zoubir A M. Source enumeration using the PDF of sample eigenvalues via information theoretic criteria[C]∥IEEE International Conference on Acoustics Speech Signal Processing, Kyoto, Japan, 2012, 2: 3361-3364. [本文引用:1]
[9]	Pesavento M, Gershman A B. Maximum-likelihood direction-of-arrival estimation in the presence of unknown nonuniform noise[J]. IEEE Transactions on Signal Processing, 2001, 49(7): 1310-1324. [本文引用:2]
[10]	Wu H T, Yung J F, Chen F K. Source number estimator using gerschgorin disks[J]. International Conference on Acoustics Speech Signal Processing, Adelaide Australia, 1994, 4(4): 261-264. [本文引用:1]
[11]	Wu H T, Yung J F, Chen F K. Source number estimator using transformed gerschgorin radii[J]. IEEE Transactions On Signal Processing, 1995, 43(6): 1325-1333. [本文引用:3]
[12]	Yung J F, Wu H T. Gerschgorin radii based source number detection for closely spaced signals[C]∥IEEE Transactions Acoustics Speech Signal Processing, Atlanta May, 1996: 3054-3057. [本文引用:1]
[13]	Gu J F, Wei P, Tai H M. Detection of the number of sources at low signal-to-noise ratio[C]∥IET Signal Processing, 2007, 1(1): 2-8. [本文引用:1]
[14]	Zoubir A, Boashash B. The bootstrap and its application in signal processing[C]∥IEEE Signal Processing Magazine, 1998, 1: 55-76. [本文引用:1]
[15]	Politis D. Computer-intensive methods in statistical analysis[J]. IEEE Signal Processing Magazine, 1998, 1: 39-55. [本文引用:1]
[16]	Aouada S, Zoubir A M, See C M S. Source detection in the presence of nonuniform noise[C]∥IEEE International Conference on Acoustics Speech Signal Processing, Montreal, Canada, 2004, 2: 165-168. [本文引用:1]
[17]	Scharf L L. Statistical Signal Processing: Detection, Estimation and Time Series Analysis[M]. Addison Wesley, 1990. [本文引用:1]
[18]	Zoubir A, Iskand er D. Bootstrap Techniques for Signal Processing[M]. Cambridge: Cambridge University Press, 2004. [本文引用:2]
[19]	Aouada S, Transkov D, Heureuse N, et al. Application of the bootstrap to source detection in Nonuniform noise[C]∥IEEE International Conference on Acoustics Speech Signal Processing, Pennsylvania, USA, 2005, 4: 997-1000. [本文引用:2]
[20]	Brcich R, Zoubir A M, Pelin P. Detection of sources using bootstrap techqiques[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 206-215. [本文引用:1]
[21]	Eforn B, Tibshirani R. An Introduction to the Bootstrap[M]. London: Chapman&Hall, 1993. [本文引用:1]

1999

0.0

... 信源数检测作为信号参数估计的先决条件,是阵列信号处理中至关重要的问题^[1,2] ...

2004

0.0

... 信源数检测作为信号参数估计的先决条件,是阵列信号处理中至关重要的问题^[1,2] ...

1956

0.0

... 最早的信源数检测问题是采用假设检验,需要人为地设置门限^[3],因而人们提出了预先设定包含门限置信区间的检测方法^[4] ...

1991

0.0

... 最早的信源数检测问题是采用假设检验,需要人为地设置门限^[3],因而人们提出了预先设定包含门限置信区间的检测方法^[4] ...

1985

0.0

... 经典的信源数检测方法以AIC和MDL信息论准则为基础^[5],AIC准则缺乏一致性,MDL准则是一致估计,但在低信噪比和小快拍数的情况下不能保证检测性能 ...

1999

0.0

2013

0.0

2012

0.0

2001

0.0

... 信源数N为未知估计量,则线阵接收的阵列信号为^[9]: ...

... 接收信号假设为零均值高斯过程^[9] ...

1994

0.0

... 盖氏圆方法^[10,11,12]能够适用于空间非均匀噪声的环境,但其在信噪比较低时常常会产生欠估计或过估计,且需要对(M-1)#cod#x000D7 ...

1995

0.0

... 盖氏圆方法^[10,11,12]能够适用于空间非均匀噪声的环境,但其在信噪比较低时常常会产生欠估计或过估计,且需要对(M-1)#cod#x000D7 ...

... )构成酉变化矩阵^[11]: ...

... _m=cm是盖氏圆半径^[11],其指出了特征值多样性和特征矢量对应空间^[16]: ...

1996

0.0

... 盖氏圆方法^[10,11,12]能够适用于空间非均匀噪声的环境,但其在信噪比较低时常常会产生欠估计或过估计,且需要对(M-1)#cod#x000D7 ...

2007

0.0

... 在许多实际的系统中,高斯数据和大样本数量的假设是无法满足的^[13],所以本文提出了一种基于假设检验的替代方法 ...

1998

0.0

... 零假设下的检验统计量的分布是使用Bootstrap方法来估计的^[14,15],这种方法对高斯分布和大部分非高斯分布都是有效的,且其优点是估计在确定样本数量下的经验分布,而不是渐进分布 ...

1998

0.0

2004

0.0

... _m=cm是盖氏圆半径^[11],其指出了特征值多样性和特征矢量对应空间^[16]: ...

1990

0.0

... 容易得到观测数据的负对数似然方程为^[17]: ...

2004

0.0

... 使用如下统计检测量^[18,19]: ...

... 4 Bootstrap对于分布的估计进行假设检验的显著度估计需要检验统计量的空域分布知识,Bootstrap方法用来进行零假设下的非参数估计^[18] ...

2005

0.0

... 使用如下统计检测量^[18,19]: ...

... 根据这种变化,进行以下一系列独立的假设检验^[19]: ...

2002

0.0

1993

0.0