基于时间反转算子分解的选择性聚焦方法

引用本文

付永庆, 刘伟. 基于时间反转算子分解的选择性聚焦方法. 2015, 45(5): 1731-1736
FU Yong-qing, LIU Wei. Selective focusing method with decomposition of the time reversal operator. Journal of Jilin University Engineering and Technology Edition, 2015, 45(5): 1731-1736 复制到剪切板

Permissions

基于时间反转算子分解的选择性聚焦方法

付永庆, 刘伟

哈尔滨工程大学信息与通信工程学院, 哈尔滨 150001

作者简介:付永庆(1956-),男,教授.研究方向:通信与信息处理,阵列信号处理.E-mail:fuyongqing@hrbeu.edu.cn

基金:国家自然科学基金项目(61172038)

摘要

为了实现电磁平面波在不同目标上的选择性聚焦,提出了一种基于波动方程时间反转不变性的时间反转算子分解算法。该算法利用天线阵列发射和接收的目标探测信号获得传输矩阵和时间反转算子,然后对该算子进行特征值分解,其中非零主特征值的个数对应目标个数,而每个非零主特征值所对应的主特征向量则包含了相应目标的方位信息。根据每个目标相对应的特征向量计算目标域中各观测点的目标函数可获得目标域中的目标函数值分布情况,并实现在不同目标处的选择性聚焦。最后,通过仿真实验验证了电磁平面波情况下基于时间反转算子分解的选择性聚焦方法的准确性和有效性。

关键词: 信息处理技术; 选择性聚焦; 时间反转算子分解; 特征向量

中图分类号:TN911 文献标志码:A 文章编号:1671-5497(2015)05-1731-06

Selective focusing method with decomposition of the time reversal operator

FU Yong-qing, LIU Wei

College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China

Abstract

In order to achieve the selective focusing on different targets in electromagnetic plane wave, a decomposition method of the time reversal operator based on the time reversal invariance of wave equation is proposed. In this method, the transfer matrix and time reversal operator are obtained by emitting and receiving the signal for detecting targets with the antenna array. Then, the time reversal operator is used to perform eigenvalue decomposition. In eigenvalue decomposition, the number of nonzero main eigenvalues is the same as the number of targets, and the main eigenvectors corresponding with these nonzero main eigenvalues contain the direction information of the targets. According to these eigenvectors of targets to calculate the objective function of every detection point in the given target area can be obtained the objective function value distribution of the target area, and achieve the selective focusing on different targets. Finally, the simulations are performed and the results show that the selective focusing method with decomposition of the time reversal operator in electromagnetic plane wave is effective.

Keyword: information processing; selective focusing; decomposition of the time reversal operator; eigenvector

Show Figures

时间反转理论由光学中的相位共轭产生, Fink等^[1]于1989年验证了时间反转的空间聚焦特性并首次给出了时间反转镜(Time reversal mirror, TRM)的概念。随后, 国内外专家在水声领域做了大量的相关研究及实验并取得了一定的研究成果^{[2, 3]}。到目前为止, 时间反转理论已经在超声碎石^[4]、无损探伤^[5]、水下目标探测^[6]、无线通信^{[7, 8]}和成像^{[9, 10]}等领域得到广泛探讨与研究。时间反转技术最主要的优点是不需要介质性质和阵列分布等先验知识就可以实现自适应聚焦^{[11, 12]}, 因此越来越受到人们的重视。对于信号反射强度不同的多个目标, 为了实现在目标上的选择性聚焦, 可通过有限次数的时间反转迭代逐渐削弱反射系数较小的目标处的相对聚焦信号能量, 最终实现在强反射目标上的选择性聚焦^[13], 但通过迭代时间反转使信号聚焦于弱反射目标处是不可能实现的。

为了实现在信号反射强度不同的多目标处的选择性聚焦, 本文提出了一种基于电磁平面波波动方程的时间反转算子分解算法, 仿真实验显示, 根据时间反转算子分解的特征值和特征向量可以有效地实现在反射系数不同的目标处的选择性聚焦。

1 波动方程的时间反转不变性

时间反转理论以波动方程的时间反转不变性为基础, 把天线阵列接收到的目标信号进行时间反转后重新发射到空间中, 则时间反转后信号经过反向传输并实现在目标处的重聚焦。

假设电磁场中的标量位函数为φ (r, t), 则在无源场区域满足的标量波动方程为:

$\begin{matrix} \nabla^{2} φ (r, t) - με \partial^{2} φ (r, t) / \partial t^{2} = 0 (1) \end{matrix}$

式中:μ 和ε 分别为介质的介电常数和磁导率; r为电磁波传播的位移矢量。

考虑平面电磁波, 则式(1)所示标量波动方程的通解为:

$\begin{matrix} φ (r, t) = f_{1} (t - r / v) + f_{2} (t + r / v) (2) \end{matrix}$

式中:f₁和f₂为任意函数; v=1/ $\begin{matrix} \sqrt[]{με} \end{matrix}$ 为电磁波传播速度。

将式(2)右边两项分别用φ ₁ $\begin{matrix} (r, t) \end{matrix}$ 和φ ₂ $\begin{matrix} (r, t) \end{matrix}$ 来表示:

$\begin{matrix} \begin{matrix} φ_{1} (r, t) = f_{1} (t - r / v) (3) \\ φ_{2} (r, t) = f_{2} (t + r / v) (4) \end{matrix} \end{matrix}$

可以看出, 式(3)和式(4)分别表示传播方向相反的两类波形, 且它们都是波动方程的解。

对式(3)和式(4)做时间反转处理, 可得:

$\begin{matrix} \begin{matrix} φ_{1} (r, - t) = f_{1} (- t - r / v) = f_{1} (- (t + r / v)) (5) \\ φ_{2} (r, - t) = f_{2} (- t + r / v) = f_{2} (- (t - r / v)) (6) \end{matrix} \end{matrix}$

可见, φ ₁ $\begin{matrix} (r, - t) \end{matrix}$ 与φ ₂ $\begin{matrix} (r, - t) \end{matrix}$ 也是波动方程的解, 且平面电磁波波动方程具有时间反转不变性。这一特性说明由目标激励发射(或反射)的每一个电磁波, 经过介质传播之后的场, 必定会存在一个时间上与之相反的场沿着相同的路径返回到目标的位置, 实现目标处的自适应重聚焦。

2 时间反转算子的分解算法

2.1 时间反转算子

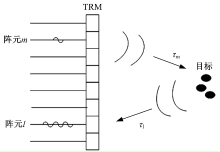
考虑一个由N个天线阵元组成的TRM阵列, 有N× N个交叉阵元脉冲响应, 如图1所示。令k_lm $\begin{matrix} (t) \end{matrix}$ 表示当一个时域delta函数作用于阵元m时, 阵元l接收到的信号。根据第1节对电磁波波动方程的描述可将平面电磁波在空间中的传输函数写成:

$\begin{matrix} h (t) = δ (t - τ) (7) \end{matrix}$

式中:τ 为电磁波的传播时延。

	Figure Option View Download New Window
	图1 阵元间脉冲响应Fig.1 Interelement impulse response

从阵元m到阵元l之间的交叉脉冲响应可以表示为:

$\begin{matrix} k_{lm} (t) = δ_{m} (t - τ_{m}) * δ_{l} (t - τ_{l}) (8) \end{matrix}$

式中:τ _m、τ _l分别为目标到第m个和第l个阵元的传播时延; * 表示卷积。

令e_m $\begin{matrix} (t) \end{matrix}$ (1≤ m≤ N), 是天线阵列的发射信号, 信号经过目标的反射后被天线阵列重新接收, 则接收信号r_l $\begin{matrix} (t) \end{matrix}$ (1≤ l≤ N), 可以表示为:

$\begin{matrix} r_{l} (t) = \overset{N}{\sum_{m = 1}} k_{lm} (t) * e_{m} (t) (9) \end{matrix}$

式(9)写成频域形式为:

$\begin{matrix} R_{l} (ω) = \overset{N}{\sum_{m = 1}} K_{lm} (ω) E_{m} (ω) (10) \end{matrix}$

用矩阵形式表示:

$\begin{matrix} R (ω) = K (ω) E (ω) (11) \end{matrix}$

式中:E $\begin{matrix} (ω) \end{matrix}$ 和R $\begin{matrix} (ω) \end{matrix}$ 分别表示N个天线阵元的发射和接收信号向量; K $\begin{matrix} (ω) \end{matrix}$ 为传输矩阵, 维数为阵元个数。

根据互易定理, 从阵元m到阵元l之间的交叉脉冲响应与从阵元l到阵元m之间的交叉脉冲响应相同, 因此传输矩阵K $\begin{matrix} (ω) \end{matrix}$ 是对称阵。

设E₀ $\begin{matrix} (ω) \end{matrix}$ 为天线阵列第一次发射的信号向量, 则经过目标反射后天线阵列的接收信号可用传输矩阵表示为:

$\begin{matrix} R_{0} (ω) = K (ω) E_{0} (ω) (12) \end{matrix}$

时域内的时间反转操作等同于频域内的相位共轭, 则天线阵列第二次发射的信号向量为第一次接收信号向量的相位共轭:

$\begin{matrix} R_{1} (ω) = R_{0}^{*} (ω) = K^{*} (ω) E_{0}^{*} (ω) (13) \end{matrix}$

经过两次时间反转处理后, 天线阵列的发射信号向量可以表示为:

$\begin{matrix} \begin{matrix} R_{2} (ω) = {(K (ω) R_{0}^{*} (ω))}^{*} = \\ K^{*} (ω) K (ω) E_{0} (ω) (14) \end{matrix} \end{matrix}$

以此类推, 经过2n次和2n+1次时间反转处理后, 天线阵列的发射信号向量可以分别表示为:

$\begin{matrix} \begin{matrix} R_{2 n} (ω) = {(K^{*} (ω) K (ω))}^{n} E_{0} (ω) (15) \\ R_{2 n + 1} (ω) = {(K^{*} (ω) K (ω))}^{n} K^{*} (ω) E_{0} (ω) (16) \end{matrix} \end{matrix}$

式中:K^* $\begin{matrix} (ω) \end{matrix}$ K $\begin{matrix} (ω) \end{matrix}$ 称为时间反转算子。

因为K $\begin{matrix} (ω) \end{matrix}$ 具有对称性, 所以有:

$\begin{matrix} \begin{matrix} {({(K^{*} (ω) K (ω))}^{*})}^{T} = {(K (ω) K^{*} (ω))}^{T} = \\ {(K^{*} (ω))}^{T} {(K (ω))}^{T} = K^{*} (ω) K (ω) (17) \end{matrix} \end{matrix}$

式中:T表示对矩阵的转置运算。

式(17)说明K^* $\begin{matrix} (ω) \end{matrix}$ K $\begin{matrix} (ω) \end{matrix}$ 是埃尔米特矩阵并可以进行对角化, 其特征向量是正交的, 特征值为实数。将时间反转算子进行特征值分解可得到与目标数目相同的非零主特征值, 其对应的主特征向量与目标存在着一一对应的关系。令λ 为时间反转算子的特征值, v $\begin{matrix} (ω) \end{matrix}$ 为相应的特征向量, 则由式(18)可知λ 为非负值。

$\begin{matrix} \begin{matrix} ‖ K (ω) v (ω) ‖^{2} = \\ {({(K (ω) v (ω))}^{*})}^{T} (K (ω) v (ω)) = \\ {({(v (ω))}^{*})}^{T} K^{*} (ω) K (ω) v (ω) = \\ {({(v (ω))}^{*})}^{T} λv (ω) = λ ‖ v (ω) ‖^{2} (18) \end{matrix} \end{matrix}$

2.2 时间反转算子的分解算法

假设目标域中共有d个目标, 各目标对信号的反射率分别为C₁, C₂, …, C_d。第i(1≤ i≤ d)个目标与接收阵列第n(1≤ n≤ N)个阵元之间的传输函数为h_in $\begin{matrix} (t) \end{matrix}$ , 其傅里叶变换为H_in $\begin{matrix} (ω) \end{matrix}$ , 则第i个目标与接收天线阵之间的传输向量为:

$\begin{matrix} H_{i} (ω) = [H_{i 1} (ω), H_{i 2} (ω), \dots, H_{iN} (ω)] (19) \end{matrix}$

如果点目标理想可分辨, 即在其中一个目标上的时间反转聚焦不会给其他目标提供能量, 则H_i $\begin{matrix} (ω) \end{matrix}$ 正交, 且传输矩阵可以写为如下形式^[13]:

$\begin{matrix} K (ω) = H^{T} (ω) CH (ω) (20) \end{matrix}$

从式(20)可以看出传输矩阵由3个矩阵组成:描述从阵列到目标的前向传输矩阵, 目标反射系数组成的反射矩阵和描述从目标到阵列的反向传输矩阵。

令天线阵列的发射信号为 $\begin{matrix} H_{i}^{*} \end{matrix} \begin{matrix} (ω) \end{matrix}$ , 那么根据传输矩阵可将天线阵列的接收信号表示为:

$\begin{matrix} S (ω) = K (ω) H_{i}^{*} (ω) (21) \end{matrix}$

则S $\begin{matrix} (ω) \end{matrix}$ 的第n个元素可以表示为:

$\begin{matrix} \begin{matrix} S_{n} (ω) = \overset{N}{\sum_{n' = 1}} K_{nn'} (ω) H_{in'}^{*} (ω) = \\ \overset{d}{\sum_{i' = 1}} \overset{N}{\sum_{n' = 1}} H_{i' n} (ω) C_{i'} H_{i' n'} (ω) H_{in'}^{*} (ω) = \\ \overset{d}{\sum_{i' = 1}} H_{i' n} (ω) C_{i'} \overset{N}{\sum_{n' = 1}} H_{i' n'} (ω) H_{in'}^{*} (ω) (22) \end{matrix} \end{matrix}$

由H_i $\begin{matrix} (ω) \end{matrix}$ 的正交性可得:

$\begin{matrix} \overset{N}{\sum_{n' = 1}} K_{nn'} (ω) H_{in'}^{*} (ω) = H_{in} (ω) C_{i} \overset{N}{\sum_{n' = 1}} {|H_{in'} (ω)|}^{2} (23) \end{matrix}$

写成矩阵形式有:

$\begin{matrix} K (ω) H_{i}^{*} (ω) = (C_{i} \overset{N}{\sum_{n' = 1}} {|H_{i n^{'}} (ω)|}^{2}) H_{i} (ω) (24) \end{matrix}$

进而可得到:

$\begin{matrix} \begin{matrix} K^{*} (ω) K (ω) H_{i}^{*} (ω) = \\ C_{i}^{2} {(\overset{N}{\sum_{n' = 1}} {|H_{in'} (ω)|}^{2})}^{2} H_{i}^{*} (ω) (25) \end{matrix} \end{matrix}$

可见, 时间反转算子对应某目标的特征向量是该目标到天线阵列之间的传输向量的共轭, 那么该特征向量与目标区域中的观测点对应的传输函数的内积在其对应的目标处将趋于最大, 可实现在该目标处的信号能量聚焦。假设目标域中共有M个目标观测点, 于是可得目标域中第j(1≤ j≤ M)个观测点处时间反转算子分解的选择性聚焦目标函数公式为:

$\begin{matrix} P_{j} (ω) = \overset{N}{\sum_{n = 1}} H_{jn} (ω) v_{i} (n) (26) \end{matrix}$

式中:H_jn $\begin{matrix} (ω) \end{matrix}$ 为天线阵列第n个阵元到目标域中第j个观测点的传输函数; v_i $\begin{matrix} (n) \end{matrix}$ 为时间反转算子分解后第i个非零特征值所对应特征向量中的第n个元素。

根据以上分析, 可将基于时间反转算子分解的选择性聚焦算法分为以下几个步骤:

(1)利用天线阵列的第一个阵元发射中心频率为ω ₀的目标探测信号, 经目标反射后被天线阵列接收。对接收信号进行傅里叶变换可得第一个阵元与所有阵元之间的交叉脉冲响应。

(2)用同样的信号对天线阵列的其他N-1个阵元进行激励, 重复步骤(1)的操作可获得传输矩阵K $\begin{matrix} (ω) \end{matrix}$ 。

(3)计算时间反转算子K^* $\begin{matrix} (ω) \end{matrix}$ K $\begin{matrix} (ω) \end{matrix}$ , 并利用式(27)将其进行特征值分解获得主特征值与主特征向量, 其中主特征值的个数即为目标个数。

$\begin{matrix} K^{*} (ω) K (ω) = v (ω) Λv {(ω)}^{- 1} (27) \end{matrix}$

(4)确定目标搜索域及各观测点。

(5)根据式(26)并利用目标所对应的主特征向量计算目标域中各观测点的目标函数值, 可取得在该目标处的选择性聚焦。

3 仿真分析

	Figure Option View Download New Window
	图2 均匀圆形TRMFig.2 Uniform circular TRM

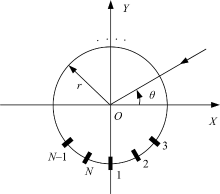
为了验证基于时间反转算子分解的选择性聚焦特性, 建立如图2所示的均匀圆形天线阵列模型, 其中N个阵元均匀分布在以r为半径的圆周上, 且阵列的几何中心与坐标原点重合。仿真实验中取N=32, r为20 m, 天线阵列发射中心频率为30 MHz的目标探测波。考虑以坐标原点为中心, 半径为20 km的圆周区域为待侦测目标区域, 且在整个圆周域上平均分布着360个观测点, 侦测步长为1° , 目标位于待侦测区域内, 且方位角分别为22° , 45° , 70° 。

为实现时间反转算子分解的选择性聚焦, 首先通过时间反转阵列的发射和接收信号获得传输矩阵, 并计算得到时间反转算子, 然后对时间反转算子进行特征值分解, 其中主特征值的个数为目标个数, 而主特征值对应的主特征向量则包含了对应目标的方位信息。利用主特征向量并根据式(26)计算各观测点的目标函数值, 其中函数值最大点所对应的观测点的方位即为该主特征值所对应目标的方位, 因此利用每个主特征值进行目标域中各观测点的目标函数值计算, 可分别实现在不同目标处的选择性聚焦。

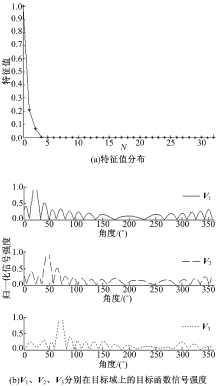首先取C₁∶ C₂∶ C₃=1∶ 0.5∶ 0.3, 通过仿真计算获得阵元间传输矩阵K $\begin{matrix} (ω) \end{matrix}$ , 则时间反转算子可以写成K^* $\begin{matrix} (ω) \end{matrix}$ K $\begin{matrix} (ω) \end{matrix}$ , 对其进行特征值分解后, 归一化特征值分布如图3(a)所示。从图中可以看出:由于目标域中只有3个目标, 所以时间反转算子分解后只有3个非零特征值。令3个大小依次排列的特征值对应的特征向量分别记为V₁、V₂和V₃, 并将这3个特征向量作为权向量分别计算目标域中的目标函数, 可得如图3(b)所示目标域中的归一化目标函数信号强度分布情况。从图中可以看出, 利用弱反射目标所对应的特征向量可以实现在弱目标处的有效聚焦, 而且利用每个主特征向量可以分别实现在相应目标处的准确聚焦, 聚焦方位分别为22° 、45° 、70° , 这说明每个主特征向量分别为天线阵列提供了相应目标的方位信息, 可以有效地聚焦在相应的目标处, 很好地实现了选择性聚焦。

	Figure Option View Download New Window
	图3 C₁∶ C₂∶ C₃=1∶ 0.5∶ 0.3时, 时间反转算子分解的选择性聚焦Fig.3 Selective focusing of decomposition of time reversal operator in C₁∶ C₂∶ C₃=1∶ 0.5∶ 0.3

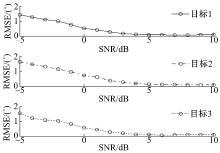
	Figure Option View Download New Window
	图4 不同信噪比下选择性聚焦的均方根误差Fig.4 RMSE of selective focusing in different SNR

为分析基于时间反转算子分解的选择性聚焦算法在不同信噪比下的聚焦性能, 与图3实验相同, 取C₁∶ C₂∶ C₃=1∶ 0.5∶ 0.3, 3个主特征向量V₁、V₂、V₃分别对应目标1、2、3, 并在仿真时加入信噪比不同的高斯白噪声。利用不同主特征向量实现其对应目标处的选择性聚焦, 并执行100次蒙特卡洛实验, 图4为不同信噪比情况下基于时间反转算子分解的选择性聚焦算法的均方根误差。从图中可以看出:随着信噪比的增加, 该算法选择性聚焦的均方根误差逐渐变小, 而且在信噪比为0 dB的情况下, 不同目标的选择性聚焦误差都在1° 以内, 显示了该算法良好的聚焦性能。

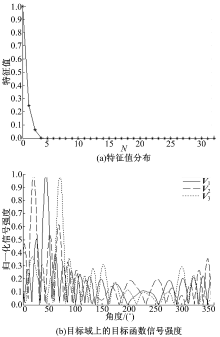	Figure Option View Download New Window
	图5 C₁∶ C₂∶ C₃=0.5∶ 1∶ 0.3时, 时间反转算子分解的选择性聚焦Fig.5 Selective focusing of decomposition of time reversal operator in C₁∶ C₂∶ C₃=0.5∶ 1∶ 0.3

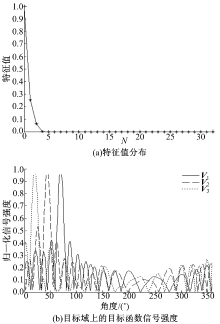	Figure Option View Download New Window
	图6 C₁∶ C₂∶ C₃=0.3∶ 0.5∶ 1时, 时间反转算子分解的选择性聚焦Fig.6 Selective focusing of decomposition of time reversal operator in C₁∶ C₂∶ C₃=0.3∶ 0.5∶ 1

利用与图3同样的方法可以获得C₁∶ C₂∶ C₃=0.5∶ 1∶ 0.3和C₁∶ C₂∶ C₃=0.3∶ 0.5∶ 1条件下的仿真结果, 如图5和图6所示。从图中可以看出:改变目标的反射系数, 时间反转算子分解算法依然可以很好地实现在各不同目标处的选择性聚焦, 只是特征向量V₁、V₂、V₃所对应的目标位置发生了改变。综合图3、图5和图6可以看出:非零特征值的大小与对应目标的信号反射率有关, 目标反射率越大, 对应的特征值也越大, 因此可以根据特征值的大小选择相应的特征向量实现在不同目标处的聚焦。

4 结束语

提出了一种基于平面电磁波波动方程时间反转不变性的时间反转算子分解选择性聚焦方法, 该方法通过对时间反转算子的分解可以获得与目标数目一致的主特征值和与目标方位一一对应的主特征向量。根据每个目标所对应的特征向量计算目标域中所有观测点处的目标函数值可以实现在各目标处的选择性聚焦。仿真实验结果显示该方法具有有效性, 利用弱反射目标所对应的特征向量可实现在弱目标处的聚焦, 利用所有的主特征向量可以实现在不同目标上的选择性聚焦, 另外, 主特征值的大小和各目标所对应的特征向量次序都与目标的反射系数有关。该方法可以用于对多个目标中的弱目标进行检测或者是对多目标进行选择性检测的情况, 具有很好的应用前景。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Fink M, Prada C, Wu F, et al. Self focusing in inhomogeneous media with time reversal acoustic mirrors[C]∥IEEE Ultrasonics Symposium Proceedings, Montreal, Que: IEEE, 1989: 681-686. [本文引用:1]
[2]	Song H C, Kuperman W A, Hodgkiss W S, et al. Iterative time reversal in the ocean[J]. Journal of the Acoustical Society of America, 1999, 105(6): 3176-3184. [本文引用:1]
[3]	Sheng X L, Bao X Z, Hui J Y, et al. Underwater Passive Location Technology Using Dummy Time-reversal Mirror[M]. Lecture Notes in Computer Science, Berlin: Springer, 2008: 605-612. [本文引用:1]
[4]	Thomas J L, Fink M. Self focusing on extended objects with time reversal mirror, application to lithotripsy[C]∥IEEE Ultrasonics Symposium Proceedings, Cannes, France: IEEE, 1994: 1809-1814. [本文引用:1]
[5]	赵乃至, 阎石, 齐霁. 基于时间反转法的管道周向裂缝损伤检测[J]. 沈阳建筑大学学报, 2013, 29(1): 44-49. Zhao Nai-zhi, Yan Shi, Qi Ji. The pipeline circumferential cracks damage detection based on time reversal method[J]. Journal of Shenyang Jianzhu University, 2013, 29(1): 44-49. [本文引用:1]
[6]	李壮, 乔钢, 王健培, 等. 基于虚拟时间反转镜的短基线定位研究[J]. 应用声学, 2012, 31(4): 256-261. Li Zhuang, Qiao Gang, Wang Jian-pei, et al. Short baseline positioning based on virtual time reversal mirror[J]. Applied Acoustics, 2012, 31(4): 256-261. [本文引用:1]
[7]	Khan W N, Zubair M, Wyne S, et al. Performance evaluation of time-reversal on measured 60 GHz wireless channels[J]. Wireless Personal Communications, 2013, 71(1): 701-707. [本文引用:1]
[8]	Chen Y, Yang Y H, Han F, et al. Time-reversal wideband communications[J]. IEEE Signal Processing Letters, 2013, 20(12): 1219-1222. [本文引用:1]
[9]	Choi H, Ogawa Y T, Ohgane T. Time-reversal MUSIC imaging with time-domain gating technique[J]. IEICE Transactions on Communications, 2012, E95-B(7): 2377-2385. [本文引用:1]
[10]	Liu X F, Wang B Z, Li J L. Transmitting-mode time reversal imaging using MUSIC algorithm for surveillance in wireless sensor network[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(1): 220-230. [本文引用:1]
[11]	Fu Y Q, Jiang Y L, Liu Z Y. Near-field source localization method and application using the time reversal mirror technique[J]. Journal of Electronics (China), 2011, 28(4): 531-538. [本文引用:1]
[12]	夏云龙, 付永庆. 时间反转算子特征值分解算法[J]. 哈尔滨工程大学学报, 2008, 29(12): 1340-1343. Xia Yun-long, Fu Yong-qing. Eigenvalue decomposition algorithm for time reversal operators[J]. Jousnal of Harbin Engineering University, 2008, 29(12): 1340-1343. [本文引用:1]
[13]	Prada C, Mannecille A, Spoliansky D, et al. Decomposition of the time reversal operator: Detection and selective focusing on two scatters[J]. Journal of the Acoustical Society of America, 1996, 99(4): 2067-2076. [本文引用:2]

1989

0.0

... 时间反转理论由光学中的相位共轭产生,Fink等^[1]于1989年验证了时间反转的空间聚焦特性并首次给出了时间反转镜(Time reversal mirror,TRM)的概念 ...

1999

0.0

... 随后,国内外专家在水声领域做了大量的相关研究及实验并取得了一定的研究成果^[2,3] ...

2008

0.0

... 随后,国内外专家在水声领域做了大量的相关研究及实验并取得了一定的研究成果^[2,3] ...

1994

0.0

... 到目前为止,时间反转理论已经在超声碎石^[4]、无损探伤^[5]、水下目标探测^[6]、无线通信^[7,8]和成像^[9,10]等领域得到广泛探讨与研究 ...

2013

0.0

. 2013, 29(1):44-49

The pipeline circumferential cracks damage detection based on time reversal method

基于时间反转法的管道周向裂缝损伤检测

Zhao Nai-zhi , Yan Shi , Qi Ji.

赵乃至, 阎石, 齐霁

目的研究采用超声导波检测管道中可能存在的周向裂纹的损伤形式,验证时间反转法在管道超声检测中的应用效果.方法建立了一套试验系统,将不同传感器接收到的声源发射信号,按其时间历程的反向过程重新向介质发射回去,使得信号先到后发、后到先发,同时回到波源处,可以有效地实现声源信号的重构,然后进行参数分析.结果缺陷深度贯穿壁厚时,导波的反射系数随周向长度的增加而同比线性增加,要比反转前反射系数增加5倍以上,通过分析缺陷周向长度对导波的反射系数的影响,可以近似估计缺陷的尺寸.结论应用信号时间反转法可以实现信号的聚焦增益,可以提高声波信号在固体介质中的信噪比,对于超声导波在管道缺陷的无损检测的进一步应用,具有很重要的现实意义,对实际工程具有具体指导作用.

... 到目前为止,时间反转理论已经在超声碎石^[4]、无损探伤^[5]、水下目标探测^[6]、无线通信^[7,8]和成像^[9,10]等领域得到广泛探讨与研究 ...

2012

0.0

. 2012, 31(4):256-261

Short baseline positioning based on virtual time reversal mirror

基于虚拟时间反转镜的短基线定位研究

Li Zhuang , Qiao Gang , Wang Jian-pei

李壮, 乔钢, 王健培

短基线声学定位技术是水下运动目标定位的重要研究内容。为了解决定位系统工作于浅水或近岸时多途扩展严重造成的时延估计误差和系统工作不稳定的问题,本文提出一种结合时间反转算法的短基线宽带应答定位技术,该方法利用短基线阵元发射宽带信号,通过应答器接收该信号时间反转处理后再返回给短基线阵元位置,实现信道多途的自适应聚焦,进而提高时延估计精度及信号检测的鲁棒性。仿真研究和湖上试验表明,该方法能够充分利用信道多途信息实现聚焦,减少信道多途对定位信号时延估计的影响,具有较强的抗噪声和多途干扰的能力。相对传统定位方法,该方法可以抑制短基线定位过程中误差及野点的产生,改善了物体定位导航的精度。

... 到目前为止,时间反转理论已经在超声碎石^[4]、无损探伤^[5]、水下目标探测^[6]、无线通信^[7,8]和成像^[9,10]等领域得到广泛探讨与研究 ...

2013

0.0

... 到目前为止,时间反转理论已经在超声碎石^[4]、无损探伤^[5]、水下目标探测^[6]、无线通信^[7,8]和成像^[9,10]等领域得到广泛探讨与研究 ...

2013

0.0

... 到目前为止,时间反转理论已经在超声碎石^[4]、无损探伤^[5]、水下目标探测^[6]、无线通信^[7,8]和成像^[9,10]等领域得到广泛探讨与研究 ...

2012

0.0

... 到目前为止,时间反转理论已经在超声碎石^[4]、无损探伤^[5]、水下目标探测^[6]、无线通信^[7,8]和成像^[9,10]等领域得到广泛探讨与研究 ...

2012

0.0

... 到目前为止,时间反转理论已经在超声碎石^[4]、无损探伤^[5]、水下目标探测^[6]、无线通信^[7,8]和成像^[9,10]等领域得到广泛探讨与研究 ...

2011

0.0

... 时间反转技术最主要的优点是不需要介质性质和阵列分布等先验知识就可以实现自适应聚焦^[11,12],因此越来越受到人们的重视 ...

2008

0.0

. 2008, 29(12):1340-1343

Eigenvalue decomposition algorithm for time reversal operators

时间反转算子特征值分解算法

Xia Yun-long , Fu Yong-qing.

夏云龙, 付永庆

... 时间反转技术最主要的优点是不需要介质性质和阵列分布等先验知识就可以实现自适应聚焦^[11,12],因此越来越受到人们的重视 ...

1996

0.0

... 对于信号反射强度不同的多个目标,为了实现在目标上的选择性聚焦,可通过有限次数的时间反转迭代逐渐削弱反射系数较小的目标处的相对聚焦信号能量,最终实现在强反射目标上的选择性聚焦^[13],但通过迭代时间反转使信号聚焦于弱反射目标处是不可能实现的 ...

... 如果点目标理想可分辨,即在其中一个目标上的时间反转聚焦不会给其他目标提供能量,则H_iω正交,且传输矩阵可以写为如下形式^[13]: ...