逆子结构分析技术是新近由国外发展起来的动力学分析方法, 该方法由试验测取系统水平和子结构水平激励-响应函数, 进而由此求解系统和各子结构动态特性^[7]。本文将此方法引入TPA方法中求悬置系统动刚度。

动力总成、车内响应子结构以及两者之间的振动传递路径可以描述为图1所示的二级结构模型, 整车模型作为一个系统, 称为一级结构。动力总成悬置之后的车身到车内响应点由于是刚性连接, 可以简化成一个整体, 本文视作子结构A。动力总成是重要激励源, 本文视作子结构B。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 汽车振动系统二级结构模型Fig.1 Two-level-structure model for vehicle vibration system

图1中, 作用于子结构B上的动态激励和在车内目标子结构(子结构A)上的动态响应分别用i(b)和o(a)表示; 子结构之间的悬置耦合点用c表示; 整车系统上由激励点到响应点的频率响应函数用H(s)表示, 称作系统水平的FRFs; 在非耦合状态下, 各子结构上由激励点到响应点的频率响应函数用H_A或H_B表示; 耦合体动刚度由K(s)表示。假定动力总成由m个悬置支撑(即有m个耦合点), 每个频率下每个悬置均有X(汽车纵向)、Y(汽车横向)、Z(垂直方向)三个方向共3m个动刚度值需要确定, 假定有n个车内响应点(每个点有X、Y和Z三个方向)需确定TPCs。为此, 根据矩阵理论分析, 提出一种求解动刚度矩阵的数学方法。先在系统水平上测量m个激励点到n个响应点的FRFs, 得到一个3n× 3m矩阵。然后, 对应地测量子结构水平FRFs:

HA, o(a)c(a), HB, c(b)i(b), HA, c(a)c(a), HB, c(b)c(b)

分别得到3n× 3m矩阵、3m× 3m矩阵、3m× 3m矩阵、3m× 3m矩阵。系统水平FRFs和悬置动刚度之间有着如下矩阵形式^[7]:

KS=(HB, c(b)i(b)[HS, o(a)i(b)]+×HA, o(a)c(a)-D)+[D]=HA, c(a)c(a)+HB, c(b)c(b)3

由于m和n往往不相等, 式(3)中使用了伪逆矩阵, 以上标“ +” 表示。得到了动刚度, 依据式(2)即可计算载荷, 再依据式(1)即可计算TPCs。

式(2)应用了动力总成悬置主、被动端的实测激励信号进行载荷计算, 信号中必然掺杂有噪声, 如果对信号进行降噪, 显然能减小偏差, 本文计算载荷前, 先对信号进行降噪处理。众多降噪方法中, Donoho提出的小波阈值降噪法^[8]使用简便且效果较好。使用该方法时, 如何选择阈值和如何进行阈值量化很大程度上确定降噪质量的好坏, 所以小波阈值降噪首先要找到一个合适的值λ 作为阈值。通常预置阈值定义为:

λ=σ2lnN4

式中:σ 为噪声的均方差; N为数据长度。

当小波系数小于λ 时, 认为主要由噪声引起, 把这部分小波系数置为零; 当小波系数大于λ 时, 认为主要由信号引起, 则这部分消息保留, 这样, 就可以得到小波系数的估计值 d^kjn∈Z。估计小波系数 d^nj硬阈值定义为:

d^nj=dnj, dnj≥λ0, dnj< λ5

阈值降噪法主要步骤如下:①信号小波分解:选择一个小波并确定一个分解层次, 然后对振动信号进行分解; ②小波分解高频系数阈值量化:对每一层高频系数选择一个阈值进行软阈值或者硬阈值量化处理; ③小波重构:根据小波分解的底层的低频系数和各层的高频系数进行一维振动信号重构。本文采用5层小波分解, 选取最优预测变量阈值heursure进行量化处理, 用symlets族sym8小波进行小波重构。

利用式(2)对每个频率的动刚度和载荷进行计算可以得到其确切值, 但计算量会很大。尤其是对于载荷计算, 因为激励信号进行了小波降噪, 更增加了计算量。将测取信号的频率范围分为若干个频段, 每个频段取一个频率, 利用上述方法对信号进行小波降噪并计算载荷, 然后基于这些计算得到的载荷利用神经模糊逻辑算法测算其他频率的载荷, 则可以避免此情况。用于计算载荷的激励信号经过小波降噪, 具有较高的精度, 以此载荷作为神经模糊逻辑算法的训练样本, 预测结果精度也会较高。

神经模糊逻辑算法将神经网络嵌入模糊控制系统中, 模糊逻辑规则建立在神经网络对大量训练数据学习基础之上, 显然比基于经验建立的规则更客观、更高效。图2为基于该方法构建的、用于测算载荷的模型示意图^[9], 测算动刚度模型与之类似。系统接收频率ω 后按事先训练好的规则进行模糊化处理(第1、2层), 并进行模糊推理输出模糊量(第3、4层), 最后进行清晰化输出载荷f(第5层)。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 神经模糊算法测算载荷模型Fig.2 Model for predicting loads using neural fuzzy algorithm

本文将神经网络与Sugeno模糊模型结合生成隶属度函数和模糊规则, 按以下步骤进行。

(1)训练数据设置

训练数据选取以上抽取若干频率ω 计算得到的载荷f, 仅选取20组(20× 2矩阵), 包含输入变量频率ω 和输出变量载荷f。生成初始FIS选用网格法, 选取7个模糊子集覆盖输入变量, 输入变量隶属函数选用钟形, 输出量隶属函数选用线性。

(2)训练方法设置

选用混合法训练数据; 由于样本数据较少, 适当提高误差精度, 取0.001; 经过尝试, 训练50次可达误差精度要求。

(3)隶属函数参数和模糊规则生成

经过训练, 系统自动得出模糊推理系统的隶属函数参数和模糊规则, 输出变量f的输出函数为ω 的数学关系式。

试验对象为一款微型客车, 动力总成前后左右各设置一个橡胶悬置。工况数据采集时, 在每个悬置的主动端和被动端各安装1个, 共安装8个3D振动加速度传感器测取信号作为传递路径输入信号。参考汽车行业标准QC/T 747-1999, 取后桥上座椅导轨为响应点, 安装1个加速度传感器测取信号。这样, 整车“ 动力总成-振动响应点” 振动系统就形成4× 3=12输入、1× 3=3输出的振动模型。采集振动信号过程同时采集发动机转速信号。为了排除路面激励影响, 使用驻车怠速工况测试振动信号。

测取系统水平FRFs时, 由于动力总成安装在机仓内, 空间狭窄, 不好使用力锤施力, 采用互逆法测量。选取曲轴左右两旁机体外壁前端、后端共4个点作为子结构B的激励输入点, 在每个点粘贴1个振动传感器。保留上述后桥上座椅导轨传感器, 在其附近施加激励, 测取所有传感器信号。由此求得1个3× 12规模的系统水平FRFs矩阵H_{S, o(a)i(b)}。

测取子结构水平FRFs时, 将动力总成用尼龙绳悬吊, 让其自由摆动。同样选取曲轴前端、后端左右两旁机体外壁共4个点作为子结构B的激励输入点, 在每个点上粘贴1个振动传感器; 保留工况数据采集时4个悬置的螺栓安装位置(动力总成侧)上的振动传感器。分别在机体外壁4个点和悬置位置4个点用力锤施力, 测取所有传感器信号, 由此求得两个12× 12规模的B子结构水平FRFs矩阵H_{B, c(b)i(b)}和H_{B, c(b)c(b)}。

相应地, 保留工况数据采集时在4个悬置的螺栓安装位置(车身侧)上振动传感器作为子结构A激励测点, 同样保留在工况数据采集时后桥上座椅导轨上振动传感器作为测取子结构A响应测点。在激励测点上用力锤施力, 测取所有传感器信号, 由此求得一个3× 12规模的A子结构水平FRFs矩阵H_{A, o(a)c(a)}和一个12× 12规模的A子结构水平FRFs矩阵H_{A, c(a)c(a)}。图3为测试过程中加速度传感器的安装位置和力锤施力位置示例。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 加速度传感器位置和力锤施力位置Fig.3 Installation situations of the acceleration sensor & hammer

为了验证用本文所提出的方法计算动刚度的准确性, 将4个悬置放在动刚度试验台上测试其动刚度, 将计算结果与试验结果比较。为与CTPA方法比较, 结合上述测试, 也按CTPA方法测试要求的FRFs。

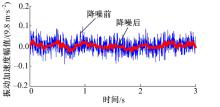
国标GB/T 4970-1996规定评价人-座椅系统振动截断频率为100 Hz, 故本文只分析100 Hz以下频段振动特性和传递路径贡献量。按第2.2节所述步骤将第3.1节所测各悬置主动、被动端加速度信号和目标点加速度信号进行小波降噪处理。图4为动力总成左后悬置被动端Z方向振动加速度信号降噪处理效果。振动信号在降噪后与原信号保持同样的走势, 但毛刺几乎已被削去, 曲线平滑成一条单行线。结果表明小波降噪参数设置合理, 降噪效果很好。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 振动加速度信号降噪效果Fig.4 De-noising effect of vibration acceleration signals

第3.1节测试所得频响函数曲线多达300多条, 图5仅示出了A子结构水平FRFs中的动力总成左后悬置X、Y和Z三个方向到响应点Z向的FRFs。

图5

Fig.5

	Figure Option ViewDownloadNew Window
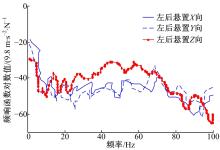	图5 左后悬置三个方向到响应点Z向频响函数Fig.5 FRFs From 3 directions of rear-left engine mount to Z-direction of response point

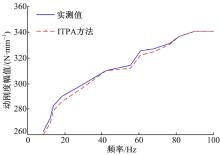
为了减少计算量, 将100 Hz分为20个频段, 每个频段计算第3个频率的动刚度, 其他频率动刚度用神经模糊逻辑算法测算。将第3.1节测试所得系统水平FRFs和子结构水平FRFs代入式(3), 计算得到逆子结构法动刚度, 然后按第2.3节方法测试其他频率动刚度。图6为按此方法所得动力总成左后悬置Z方向动刚度。为便于比较, 试验实测所得动刚度也示于同一图中。由图6可见, 两种方法得到的曲线走势一致, 70 Hz以下频段, 逆子结构方法得到的曲线与实验所得曲线有一定偏差, 可能由于信号掺杂有噪声、信号之间存在耦合等原因造成; 70 Hz频段以上吻合较好。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 左后悬置Z方向动刚度Fig.6 Dynamic stiffness of Z-direction of rear-left mount

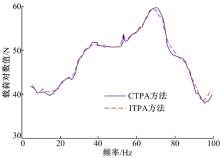
同样将100 Hz划分为20个频段, 基于第3.2节降噪后振动信号和第3.3节所得动刚度, 计算每个频段中1个频率的载荷, 按第2.3节所述方法测算其他频率载荷。图7为动力总成左后悬置Z方向的载荷。将同对象、同工况用CTPA方法得到的载荷也示出于同一图中。由图7可见, 两种方法得到的曲线走势一致,

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 动力总成左后悬置Z方向载荷Fig.7 Loads at Z-direction of front-left engine mount

在38、65和75 Hz附近, ITPA方法得到的曲线与CTPA方法得到的曲线有小幅偏离, 其他频段两曲线吻合较好。

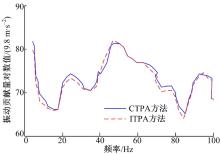
有了第3.1节测试所得FRFs和第3.4节计算所得载荷, 利用式(1)可计算出各传递路径对响应点的振动贡献量。图8为采用ITPA方法和CTPA方法得到的动力总成左后悬置Z向到座椅导轨Z向的贡献量幅值。由图可见, 两种方法得到的TPCs总体上走势一致, ITPA方法所得曲线在约15~20 Hz、50~60 Hz和90~00 Hz频段与CTPA方法所得曲线吻合很好, 在其他频段出现小幅偏离现象。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 左后悬置Z向到座椅导轨Z向振动贡献量Fig.8 Vibration contributions at Z-direction of the track of seat from Z-direction of rear-left engine mount

本文提出以神经模糊逻辑算法测算悬置动刚度和载荷, 代替实际数据的计算, 明显减少了计算量, 但同时, 理论上会产生误差。以本文的动刚度和载荷处理为例, 将100 Hz划分为5个频段, 每个频段计算一个频率的数据, 计算量仅为1/5。模糊逻辑算法运用过程需经历测算模型构建、数据训练和结果预测步骤, 工作量无法与动刚度或载荷计算明确对比, 从本文进行数据处理的经历看, 测算完所有载荷数据与计算2个频率载荷的时间相当, 故大体上可以认为, 使用神经模糊逻辑算法处理数据至少可以减少一半工作量。

决定系数可以衡量两个变量相关的密切程度, 其值介于0~1之间, 越接近1表明两个变量间相关越密切。一般认为, 决定系数大于0.8, 由模型得到的数据就令人满意^[10]。决定系数由式(6)计算得到:

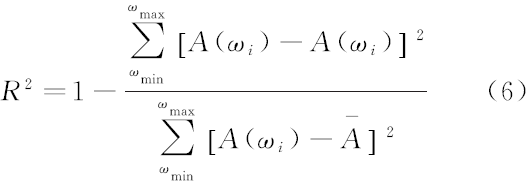
式中:A(ω _i)为某频率由计算或测算得到的动刚度、载荷或TPCs; A (ω _i)为对应的标杆值, 即试验实测动刚度和由CTPA方法所得载荷或TPCs; A-为全频率下的计算和测算平均值。

由式(6)计算得到的动刚度、载荷和TPCs决定系数分别为0.94、0.92和0.91, 均大于0.9, 表明结果有较高的精度。