多方式诱导下通勤出行链交通方式组合选择行为模型

引用本文

赵丹, 邵春福, 王军利, 李娟, 王博彬. 多方式诱导下通勤出行链交通方式组合选择行为模型. 2015, 45(6): 1763-1770
ZHAO Dan, SHAO Chun-fu, WANG Jun-li, LI Juan, WANG Bo-bin. Modelling combined mode choice behavior of commute trip chain under multi-modal guidance. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1763-1770 复制到剪切板

Permissions

多方式诱导下通勤出行链交通方式组合选择行为模型

赵丹¹, 邵春福², 王军利¹, 李娟², 王博彬²

1. 中国人民公安大学交通管理工程系, 北京 102623

2.北京交通大学城市交通复杂系统理论与技术教育部重点实验室, 北京 100044

作者简介:赵丹(1983-),女,博士研究生,讲师.研究方向:城市交通规划与管理.E-mail:zhaodanbjtu@163.com

基金:国家自然科学基金项目(51178032); “973”国家重点基础研究发展计划项目(2012CB725403); 国家“十二五”科技支撑计划项目(2013BAG18B01); 2013年度教育部人文社会科学研究青年基金项目(13YJCZH082); 中国人民公安大学基本科研业务费项目(2014JKF01130)

摘要

从出行链的角度出发研究多方式诱导信息对通勤出行方式选择的影响。通过RP&SP调查获取通勤者的实际和意向出行链数据,建立了综合考虑尺度系数差异、非显化异质性效应和参照依赖效应的mixed logit模型,并设计仿真方法求解。结果表明,尺度系数差异解释了RP数据与SP数据融合时隐含的方差差异;异质性和参照依赖效应的引入可以度量偏好差异较大的随机变量的影响程度,反映随机变量的偏好分布;综合考虑3种因素的mixed logit模型比多项logit模型和普通mixed logit模型的精度高,解释能力更强。参数标定结果表明:多方式诱导信息服务对引导小汽车通勤出行链转向其他交通方式有积极作用,有利于从源头上缓解道路交通拥堵。

关键词: 交通运输系统工程; 交通方式组合; mixed logit模型; 出行链; 融合数据; 交通信息; 尺度系数

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2015)06-1763-08

Modelling combined mode choice behavior of commute trip chain under multi-modal guidance

ZHAO Dan¹, SHAO Chun-fu², WANG Jun-li¹, LI Juan², WANG Bo-bin²

1.Traffic Management Engineering Department, People's Public Security University of China, Beijing 102623, China

2. MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology, Beijing Jiaotong University, Beijing 100044, China

Abstract

To study the influence of multi-modal guidance information on the travel mode of commuters from the viewpoint of trip chain, A Revealed Preference (RP) and Stated Preference (SP) survey was carried out to get the revealed and stated trip chain data. Then a mixed logit model, which takes scale parameter difference, heterogeneity and reference dependence effect into account, was established. A simulation method was proposed to complete estimation. The estimation results show that the introduction of scale parameter difference is helpful to explain the unobvious variance differences between RP data and SP data when they are combined together; the adoption of heterogeneity and reference dependence effects are not only conductive to measure the impacts of some variables, whose random preferences vary obviously across individuals, more accurately, but also benefits to reflect the preference distribution of random variables. The accuracy and predictive capacity of the mixed logit model considering the three aspects are better than the multinomial logit model and the ordinary mixed logit model. It is also manifested that multi-modal guidance information service contributes to encourage commuters to shift from car trip-chain to other modes, and helps to ease traffic congestion at source.

Keyword: engineering of communication and transportation system; combined travel mode; mixed logit model; trip chain; combined data; traffic information; scale parameter

Show Figures

0 引言

通勤出行链(Commute trip chain)是指通勤者以工作单位为停驻点, 从家出发再返回家的活动和出行组合^[1]。出行链中每次出行选择的出行方式构成的组合即为出行链交通方式组合。一般, 通勤者第一次出行选择的交通方式会对整条出行链的交通方式起到决定性作用。例如, 诱导通勤者第一次出行选择公共交通, 则其后续选择公共交通的可能性变大, 可以达到从源头上控制小汽车使用量的目的。

目前城市交通诱导信息内容和服务对象均比较单一, 主要为道路交通使用者服务。针对这种情况, 本文提出多方式诱导的概念, 其实质是多种交通方式运行和运营信息的综合利用, 且形式上保证实时动态。其中的多方式既指信息提供媒介的多样性, 也蕴含信息内容与多类交通方式相关的含义。多方式诱导从优化出行链的角度出发, 通过提供出行前和出行中的动态信息服务谋求减少机动车出行, 增加公交系统和换乘出行。但信息能否发挥作用取决于通勤者的反应, 因而研究多方式诱导下的通勤者的选择行为十分必要。

目前大多数文献的研究对象均为单次出行的交通方式选择^{[2, 3, 4]}, 没有延伸到出行链范畴, 割裂了出行间的相互联系。并且, 本文的背景条件— — 多方式诱导, 是尚未实施的智能交通手段, 该背景下的出行行为数据只能依靠RP(Revealed preference)调查与SP(Stated preference)调查相结合的方法获取。RP-SP融合数据本身的特性对模型有一定要求, 大量文献忽略了这些特性, 仅采用多项logit(Multi-nominal logit, MNL)^[5]模型、巢式logit(Nested logit, NL)^[6]模型和一般mixed logit模型^[7]直接应用融合数据, 降低了模型的解释能力和精度。

本文基于多方式诱导下通勤出行链调查数据, 深入分析了RP-SP融合数据特性, 建立了综合考虑尺度系数差异、非显化异质性效应和参照依赖效应的mixed logit模型。研究了多方式诱导下通勤出行链交通方式组合选择行为, 分析其内在规律, 并论证了模型的优越性。

1 RP-SP融合数据及离散选择模型

RP数据, 又称实际偏好数据, 是根据现有交通条件设置选择集, 通勤者的选择结果反映的是实际偏好, 该方法在社会经济环境变化不大或没有新的政策实施的情况下, 可以很好地用于分析出行行为。SP数据, 又称意向偏好数据, 在研究对象区域尚未达到某标准或未实施某政策时, 给出假想选择方案集, 得到出行者的意愿偏好, 以弥补RP数据的不足。在RP数据中融入SP数据, 不仅能够消除单独使用SP数据产生的偏差, 也增强了模型对出行环境变化下出行者潜在选择行为的预测和解释能力^{[4, 8]}, 尤其是两种数据反映出的选择行为受到同一变量的影响近似相同时, 优势更加明显^{[9, 10]}。纵然RP-SP融合数据具备很多优点, 但以下几个问题不容忽视:

(1)尺度系数差异。效用函数建立过程中, 难以测量和量化的影响因素通常作为非显化效用被计入选择方案效用函数的随机误差项中。尺度系数来源于误差项的分布, 与误差项的方差成反比^[11]。由于RP数据和SP数据收集方法、选择方案设置不同, 二者随机误差项的方差必然存在差异, 因此使用RP-SP融合数据时必须考虑二者尺度系数的差异。

(2)被访者的非显化异质性效应。每个通勤者做出选择时都存在一些难以观测到的偏好差异, 称为非显化异质性。例如, 更愿意使用小汽车, 为个人偏好异质; 对费用变化十分敏感, 一旦出行费用增加, 便会改变选择结果, 为属性偏好异质。非显化异质性效应存在于RP和SP调查的各个环节, 很多假设出行者具有共同偏好的模型被证实精度低于考虑异质性的模型^{[8, 10, 12]}。

(3)SP选择结果对RP选择结果的参照依赖性。被访者的实际出行经验会对虚拟情景下的选择产生一定作用, SP选择结果受到RP选择结果的影响称为参照依赖效应。若不将参照依赖效应作为单独的变量在效用函数中列出, 这部分影响会被误差项分担, 由此降低模型精度; 并且, 数据集中被访者的选择行为惯性的程度也不完全相同, 建模时还要考虑参照依赖效应的异质性^[13]。

基于效用最大化理论的离散选择模型是分析出行行为的主要工具。早期的研究多使用MNL模型建立RP-SP融合数据模型, 其中一些文献直接忽略尺度系数差异^{[4, 5]}, 还有一些通过改变SP数据的尺度以保证某些关键变量的系数与RP数据接近, 然后将新的SP数据和RP数据融合进行参数估计^{[14, 15]}, 但MNL模型完全不能解释异质性效应, 且存在IIA(Independent from irrelevant alternative)特性。Hensher和Bradley^[6]利用NL模型解决了尺度系数差异的问题, 但其不能有效地解释SP数据集中重复观测同一对象时, 数据间可能存在的相关性, 也不能考虑个体异质性。基于上述研究, Brownstone^[16]利用假设待估参数为随机分布的mixed logit模型使RP数据和SP数据得到了更好的融合, 不仅避免了IIA特性, 也突破了非显化异质性限制问题。随后, mixed logit模型在RP-SP融合数据领域得到了广泛应用^{[8, 9, 10]}; 但是, 这些研究大多仅考虑非显化异质性, 在包容RP-SP融合数据的尺度系数差异和参照依赖效应的特性上显得不够全面。基于上述分析, 本文旨在建立一个包含尺度系数差异、非显化异质性和参照依赖效应的改进mixed logit模型。

2 基于RP-SP融合数据的mixed logit模型

2.1 模型建立

结合前面提到的RP-SP融合数据的3点特性, 建立mixed logit模型的效用函数表达式为:

$\begin{matrix} U_{int} = β_{n} X_{int} + θ_{n} [(1 - δ_{nt}^{RP}) (\sum_{t}^{T} δ_{nt}^{RP} Y_{int})] + ε_{int} (1) \end{matrix}$

式中:下角i表示方案; n表示通勤者; t表示场景。式中的选择效用由3部分构成:

(1)显化效用β _n、X_int。β _n和X_int分别为关于选择方案影响因素的行向量和列向量, β _n是服从某一分布的随机参数向量, 随通勤者n的不同而变化, 与选择方案i和场景t无关, 体现了异质性效应。β _n固定与否是mixed logit与MNL模型的根本差别。

(2)参照依赖效应θ _n[(1- $\begin{matrix} δ_{nt}^{RP} \end{matrix}$ )( $\begin{matrix} \sum_{t}^{T} \end{matrix} \begin{matrix} δ_{nt}^{RP} \end{matrix}$ Y_int)]。其中, θ _n表示衡量通勤者参照依赖效应的随机参数, θ _n> 0说明被访者做出的决策具有惯性, 即SP选择与RP选择差异较小; θ _n< 0说明被访者在提供新的服务或政策的情况下, 倾向于放弃现有选择, 寻找替代选项; $\begin{matrix} δ_{nt}^{RP} \end{matrix}$ 为指示变量, 当场景t的选择方案与RP选择方案一致时, $\begin{matrix} δ_{nt}^{RP} \end{matrix}$ =1, 否则为0; Y_int也是指示变量, 当通勤者n在场景t中选择了方案i时, 则Y_int=1, 否则为0。

(3)误差项ε _int。ε _int与β _n和X_int独立, 包含了能够影响选择结果却难以测得的变量; 对于任意通勤者和交通方式, 同一场景t中的ε _int独立且服从同一Gumbel分布, 不同场景中ε _int也相互独立, 但其分布参数不一定相同; ε _int的尺度系数λ _nt定义为:

$\begin{matrix} λ_{nt} = λ (1 - δ_{nt}^{RP}) + δ_{nt}^{RP} (2) \end{matrix}$

式中, λ 为SP数据的尺度系数。λ _nt允许RP数据和SP数据的尺度系数不同, 一般设RP数据的尺度系数为1, 然后再求λ 。两种数据尺度参数的比值(用φ 表示)用于比较二者方差的大小, φ > 1说明RP数据的方差大于SP数据; φ =1说明二者方差相等; φ < 1说明SP数据方差更大。

令:

$\begin{matrix} \begin{matrix} \{\begin{matrix} {\tilde{β}}_{n} = [β_{n}, θ_{n}] \\ Z_{int} = [\begin{matrix} X_{int} \\ (1 - δ_{nt}^{RP}) \times (\sum_{t}^{T} δ_{nt}^{RP} Y_{int}) \end{matrix}] \end{matrix} (3) \\ 则 : U_{int} = {\tilde{β}}_{n} Z_{int} + ε_{int} (4) \end{matrix} \end{matrix}$

假设 $\begin{matrix} {\tilde{β}}_{n} \end{matrix}$ 已知, 则通勤者n在场景t中选择方案i的条件概率S_int表示为:

$\begin{matrix} \begin{matrix} S_{int} = \frac{\exp ({\tilde{β}}_{n} Z_{int})}{\sum_{j} \exp ({\tilde{β}}_{n} Z_{int})} = \\ \frac{\exp (β_{n} X_{int} + θ_{n} [(1 - δ_{nt}^{RP}) (\sum_{t}^{T} δ_{nt}^{RP} Y_{int})])}{\sum_{j} \exp (β_{n} X_{jnt} + θ_{n} [(1 - δ_{nt}^{RP}) (\sum_{t}^{T} δ_{nt}^{RP} Y_{int})])} (5) \end{matrix} \end{matrix}$

那么在 $\begin{matrix} {\tilde{β}}_{n} \end{matrix}$ 未知的情况下, 通勤者n在场景t中选择方案i的非条件概率为:

$\begin{matrix} P_{int} (σ) = \int S_{int} ({\tilde{β}}_{n}) f ({\tilde{β}}_{n} |σ) d {\tilde{β}}_{n} (6) \end{matrix}$

式中:f( $\begin{matrix} {\tilde{β}}_{n} \end{matrix} \begin{matrix} |σ \end{matrix}$ )为关于 $\begin{matrix} {\tilde{β}}_{n} \end{matrix}$ 的分布密度函数, σ 为随机向量 $\begin{matrix} {\tilde{β}}_{n} \end{matrix}$ 的均值和方差, 估计σ 就是模型参数标定的过程。

2.2 模型估计方法

由于式(6)中 $\begin{matrix} {\tilde{β}}_{n} \end{matrix}$ 的维数不固定, 解析法求积分很困难, 一般采用仿真方法进行求解。对于任意给定的σ , 只要模拟时抽样方法合适, 随着仿真抽样次数的增加, P_int的仿真值可以无限接近实际值。关于抽样方法的选取, 文献[8, 12, 13]采用拟蒙特卡洛法(Quasi-MONTE Carlo)抽取普通或变序Halton序列估计模型参数, 存在的问题是:随模型变量个数的增多, Halton序列中相邻两维随机数的相关性变大, 模型偏差也增大。Latin超立方序列抽样法(Modified latin hypercube sampling, MLHS)采用分层技术, 可以有效降低随机序列相关性, 估计样本的均值和方差时对样本数量的节省也非常显著^[17]。利用MLHS法抽样并估计模型参数的步骤如下:

(1)给予σ 初值, 利用Latin超立方序列抽样法从f( $\begin{matrix} {\tilde{β}}_{n} \end{matrix} \begin{matrix} |σ \end{matrix}$ )中抽取拟随机序列 $\begin{matrix} {\tilde{β}}_{n}^{k} \end{matrix}$ , k为抽取次数, k≥ 1;

(2)根据 $\begin{matrix} {\tilde{β}}_{n}^{k} \end{matrix}$ 的值, 按照式(5)计算条件概率S_int( $\begin{matrix} {\tilde{β}}_{n}^{k} \end{matrix}$ );

(3)重复K次步骤(1)和(2), 取K次抽样的算术平均值作为仿真概率值 $\begin{matrix} {\hat{P}}_{int} \end{matrix}$ , 如式(7)所示:

若 $\begin{matrix} {\hat{P}}_{int} \end{matrix}$ 的方差较大, 可适当增加抽样次数。

(4)确定通勤者n在场景t下的选择结果, 建立通勤者n的极大似然函数, 如式(8)所示:

$\begin{matrix} L_{n} (σ) = \overset{T}{\prod_{t}} \overset{I}{\prod_{i}} ({\hat{P}}_{int})^{d_{int}} (8) \end{matrix}$

式中:d_int为指示变量, d_int=1表示通勤者n在场景t中选择了方案i, 否则为0。

(5)根据式(8)构造模型的仿真对数极大似然函数:

(6)不断改变式(9)中σ 的值, 利用梯度法使LL(σ )取得最大值。

3 多方式诱导下通勤出行链调查

3.1 选择方案

调查中出行链交通方式组合分为3类:

(1)小汽车:出行链中所有出行均使用小汽车, 没有使用轨道交通、路面公交、出租车。

(2)停车换乘公共交通(P+R换乘):①出行链中某次出行使用小汽车(公共交通), 而其他出行使用公共交通(小汽车); ②出行链中某次出行既使用了小汽车又使用了公共交通。

(3)公共交通:出行链中的每次出行均使用公共交通, 并且完全没有使用小汽车。

由于调查对象为当日使用过小汽车的通勤者, 因此设置RP调查部分出行链交通方式组合选择方案集为{小汽车, P+R换乘}; SP调查询问了小汽车通勤者选择公共交通方式的意愿, 设置该部分出行链交通方式组合选择方案集为{小汽车, P+R换乘, 公共交通}。

3.2 调查方法及样本选取

选取周边配套交通方式完备的北京市回龙观大型社区作为调查区域, 实施网络调查, 调查软件内嵌RP调查和SP调查两个模块, 如图1所示。图中, RP调查包含了3部分内容。其中, 实际出行链部分包含了通勤者当天所有出行使用的交通方式、行程时间及费用等信息, 进而统计整条出行链的方式组合、时间、费用。多方式诱导需求调查则是基于前面得到的实际出行链, 在每次出行前和出行中向被访者提供图中所示的8种信息, 被访者根据需要选择其中3项, 然后采用均匀设计的方法将3个被选项组合成不同SP调查场景, 获取被访者在这些假想场景下的出行行为, 得到被访者的意向出行链。SP调查情景主要根据通勤者每次出行前和出行中选择的诱导信息项产生, 调查场景中信息项的值由调查软件随机生成, 生成规则如表1所示。

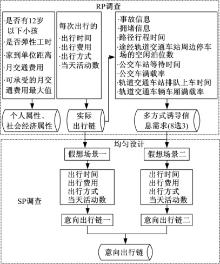	Figure Option View Download New Window
	图1 通勤出行链RP and SP网络调查模块和内容Fig.1 RP and SP online survey module and investigation contents of commute trip chain

表1 SP调查场景中随机数的生成规则 Table 1 Random number generation rules in SP choice situation

表1中, H_RP为与实际出行链相对应的该次出行的行程时间。考虑到出行链中第一次出行方式对后续方式选择的重要影响, 整理数据时主要选取SP调查中第一次出行前和第一次出行中的选择行为数据, 得到两条意向出行链。

调查于2012年6~8月实施, 回收的367份合格问卷中有效问卷175份。最终本文应用的数据为:RP数据175条, SP数据350(175× 2)条。

4 模型参数标定及解释

4.1 模型变量

考虑到出行链整体与单次出行的差异, 以及RP-SP融合数据本身的特性, 确定影响通勤出行链交通方式组合选择的变量及其说明(见表2)。每个通勤者面临的SP调查场景由其选择的多方式诱导信息项决定, 若信息项选择不同, 则场景不同。为了避免场景不同导致的模型形式差异, 与时间相关的信息项均计入出行链时间, 以变量X₇的形式带入模型。调查中拥挤度等信息项被选择的频率较低, 对应数据稀少, 本文采用引入常数项的方法对这些因素产生的作用做整体衡量。

表2 模型变量说明 Table 2 Explanations of variables in the mixed logit model

构造选择方案的效用函数U_int, 分别是:RP数据中小汽车和P+R换乘的效用函数U₁_n_{, RP}和U₂_n_{, RP}; SP数据中小汽车、P+R换乘和公共交通的效用函数U₁_n_{, SP}、U₂_n_{, SP}和U₃_n_{, SP}。

4.2 模型参数标定

设定抽样次数K=525, 对数似然函数收敛标准为相邻两次迭代系数估计值的改变量Δ $\begin{matrix} {\tilde{β}}_{n} \end{matrix}$ ≤ 0.000 001。假设 $\begin{matrix} {\tilde{β}}_{n} \end{matrix}$ 服从正态分布, 求解模型参数, 并进行t检验(当 $\begin{matrix} |t| \end{matrix}$ ≥ 1.96时, 说明系数对应的变量在95%的检验水平上对模型有显著影响)。剔除影响不显著的变量X₁和X₅, 保留其他影响显著的变量。X₁取值1通常代表通勤者活动的增加(接送孩子上下学), 则X₁与X₆可能存在共线性, 导致mixed logit模型中该变量的显著性被削弱; X₆不能通过检验表明距离对通勤出行链交通方式组合选择的影响微弱。

表3给出了4种模型的参数估计结果。模型1未考虑RP和SP数据集的方差差异, 直接将二者合并, 建立MNL模型; 模型2假设RP、SP数据集的方差不同, 用尺度系数乘以SP数据, 使之具有与RP数据相同的方差, 然后建立尺度化MNL模型, 并估计系数, 详细步骤参见文献[15]; 模型3为包含尺度系数差异和通勤者对各选择方案本身及某些属性偏好(异质性)的mixed logit模型, 但没有考虑SP调查中被访者的参照依赖效应; 模型4为综合考虑上述3种因素的mixed logit模型。

表3 四种通勤出行链交通方式组合选择模型的参数估计结果 Table 3 Four different models’ estimation results related to combined mode choice of commute trip chains

参数	变量	U_int	模型1	模型2	模型3			模型4
参数	变量	U_int	参数	参数	均值		标准差	均值	标准差
固定参数	$\begin{matrix} \frac{X_{2}}{\ln X_{3}} \end{matrix}$	U₂_n_{, RP}, U₂_n_{, SP}	1.994(6.496)	2.745(6.062)	3.547(4.547)	-		5.599(4.798)	-
	X₄	U₂_n_{, RP}, U₂_n_{, SP}	-0.414 (-1.328)	-0.636 (-1.452)	-0.875 (-1.590)	-		-1.827 (-2.239)	-
	X₆	U₁_n_{, RP}, U₁_n_{, SP}	1.635(5.975)	2.538(5.877)	3.679(4.181)	-		4.961(3.876)	-
	CC_RP	U_1n,_RP	2.295(4.531)	2.251(3.078)	2.877(2.560)	-		4.176(2.747)	-
随机参数	X₇	U₁_n_{, RP}, U₂_n_{, RP}, U₁_n_{, SP}, U₂_n_{, SP}, U₃_n_{, SP}	-0.020 (-3.564)	-0.040 (-4.449)	-0.259 (-5.220)	0.124 (5.236)		-0.226 (-4.346)	0.149 (4.257)
	X₈₁	U₁_n_{, SP}	-0.271 (-4.396)	-0.489 (-4.446)	-0.487 (-3.149)	0.140 (4.325)		-0.649 (-2.671)	0.184 (1.975)
	X₈₂	U₂_n_{, SP}	0.163 (4.848)	0.289 (4.900)	0.237 (2.499)	0.109 (2.104)		0.242 (2.327)	0.123 (2.156)
	X₈₃	U₃_n_{, SP}	-0.121 (-2.326)	-0.217 (-2.339)	-0.443 (-2.152)	0.280 (2.070)		-0.235 (-2.033)	0.148 (1.992)
	Y	U₁_n_{, SP}, U₂_n_{, SP}	-	-	-	-		11.754 (3.561)	5.617 (2.472)
	CC_SP	U₁_n_{, SP}	3.639 (6.602)	5.919 (6.819)	6.281 (4.340)	0.917 (1.981)		9.478 (4.183)	1.789 (2.523)
	PC_SP	U₃_n_{, SP}	4.140 (7.634)	6.317 (7.463)	7.238 (4.837)	1.539 (2.445)		8.013 (3.924)	3.051 (2.754)
其他统计量	φ		1	0.545(0.743)	1.075(2.146)			1.213(2.102)
	LL_max		-304.941	-297.210	-194.818			-126.114
	L(0)		-363.902	-363.902	-363.902			-363.902
	ρ ²		0.162	0.183	0.465			0.653

表3 四种通勤出行链交通方式组合选择模型的参数估计结果 Table 3 Four different models’ estimation results related to combined mode choice of commute trip chains

表3中, 第3列U_int表示变量所在的效用函数; 尺度系数比φ 用于分析RP数据和SP数据的方差情况, ρ ²用于检验模型精度高低, ρ ²称为优度比, 计算公式为:

$\begin{matrix} ρ^{2} = 1 - [\frac{L L_{\max}}{L (0)}], L (0) = - Sln 2 (10) \end{matrix}$

式中:LL_max为对数似然函数的最大值; S为样本量(本文中S=525); L(0)为所有变量系数均为0时的对数似然函数值。

ρ ²越大模型精度越高。一般认为ρ ²的值大于0.2, 模型精度即达到标准^[18]。

4.3 结果分析

分析表3中数据, 解释各变量对通勤出行链交通方式组合选择产生的影响, 比较模型的精度。

(1)模型精度比较分析

从模型1到模型4, 模型精度逐渐增大, 且mixed logit模型的精度整体高于MNL模型。考虑参照依赖效应的mixed logit模型精度最高, 说明此变量的引入对解释通勤出行链交通方式组合选择行为及提高模型精度大有帮助。

(2)数据方差比较分析

尺度系数比φ 用于比较RP数据和SP数据的方差。模型1直接假设二者的方差相等, 因此φ =1; 模型2的尺度系数比小于1, 说明尺度化MNL模型中SP数据集的方差更大, 但其t检验结果不显著, 无法拒绝RP和SP数据集具有相同的方差的假设; 两个mixed logit模型的尺度系数均大于1, 表明mixed logit模型中RP数据集方差更大。两类模型所得结果截然相反的原因可解释为:与MNL模型相比, mixed logit模型的非显化效用被随机参数部分和误差项分为两块, 随机参数部分有效分担了在MNL模型中全部来自于误差项的方差。模型4的尺度系数比大于模型3, 说明被访者的选择习惯(参照依赖效应)是非显化效用的重要组成部分, 故而成为影响方差大小的重要因素。参照依赖效应的显化可以降低误差项的方差。

(3)固定参数的影响

分析出行链费用X₂/lnX₃(X₃为月最大可承受交通费用)对P+R换乘模式的影响时发现:通勤者面临出行链费用相等的情况时, 其月交通费用的承受能力越小, 选择P+R换乘模式完成出行链的可能性越大; 当通勤者对月交通费用的承受能力相同时, 出行链费用越高, 通勤者选择P+R换乘方式完成出行链的可能性越大。弹性工时X₄对P+R换乘模式的选择具有显著的负效用, 尤其是在仅有两个选择方案的RP调查中, 工作时间没有严格规定的通勤者更倾向于选择小汽车完成出行链。活动引发出行, 出行链包含的活动数(X₆)越多, 则出行次数越多, 为了避免时间成本上升以及换乘、等待带来的额外体力消耗, 通勤者倾向于选择更加舒适便捷的小汽车完成出行链。CC_RP是U₁_n_{, RP}的固定项, 用于概括除模型变量之外其他所有因素产生的影响, 当CC_RP被设为随机参数时, 均值和方差均未通过检验, 因而确定其为固定参数, CC_RP大于0说明还有其他因素对小汽车方式的选择产生正向影响, 有可能是小汽车本身的优势, 也有可能是通勤者自身特性。

(4)随机参数的影响

出行链时间X₇对3种交通方式的选择都有显著的负作用, 而泊位数信息的影响则各不相同。轨道交通车站周边停车场的可用泊位数越多, 选择小汽车和公共交通方式的概率越下降, 但选择P+R换乘方式的概率增加, 这一结果肯定了泊位数信息对引导通勤者减少使用小汽车有正面作用。对于基础设施建设的启示是:扩大P+R换乘停车场的规模, 有利于促进通勤者从单纯的私人交通向公共交通方式转移。

CC_SP和PC_SP均大于0, 可知存在除模型变量以外的其他因素对两种方式的选择有正影响, 二者的标准差全部通过检验, 表示样本对小汽车和公共交通的偏好异质性是显著的, 但PC_SP的标准差很大, 反映出样本对两种交通方式的偏好态度正负并存。

参照依赖效应(Y)系数的均值为正, 说明样本整体的选择惯性较强, 大部分样本在SP场景中做出的选择与其实际选择行为一致, 换言之, 大部分使用小汽车和P+R换乘模式完成出行链的通勤者不会轻易放弃现在的选择; 参照依赖效应的标准差很大, 说明存在部分通勤者对目前采用的交通方式并不满意, 这部分人更倾向于放弃当前选择, 表现出对新交通方式的偏好, 这也是PC_SP为正数的原因。

考虑到4个模型的随机误差项方差不同, 不能以同一变量在不同模型中参数值的大小来比较其影响程度的高低(横向比较)。但是, 可以通过比较同一模型中不同变量参数值的大小(纵向比较)来判断通勤者对各影响因素变量的偏好。显然, 与泊位数信息相比, MNL模型中出行链时间对通勤出行链交通方式组合选择的影响非常微弱, 远低于mixed logit模型中此变量产生的影响; 这一现象表明:考虑个体异质性的模型可以更加准确地度量某些变量的作用, 而全部样本都具有相同的偏好(全部倾向于选择出行链时间最短的交通方式)的假设显然不合理。并且, 相对于CC_SP, 模型4中PC_SP的影响有所下降, 再次验证了样本整体具有较强选择惯性的事实, 即:公共交通方式是RP场景中没有的选择方案, 保持当前选择会降低通勤者对该新交通方式的偏好。

5 结论

(1)尺度系数比指标反映了RP数据与SP数据在融合时隐含的差异, 而异质性和参照依赖效应的引入则提高了模型精度, 不仅帮助mixed logit模型准确度量了随机偏好差异较大的变量的影响程度, 也可以根据随机变量的标准差判断出通勤者对出行链交通方式组合选择的偏好态度是否一致。

(2)模型变量参数估计结果表明:调查对象群体对小汽车出行链的正向偏好比较一致, 对公共交通的偏好态度正负并存, 选择行为惯性较强。当诱导信息显示可用泊位充足时, 通勤者选择P+R换乘的概率明显增加, 可知此信息服务有利于引导通勤出行链从小汽车转向其他交通方式; 减少每天的活动数可以降低通勤者使用小汽车的概率或频率, 相应地, 选择P+R换乘和公共交通的可能性会增加, 达到从源头上缓解拥堵的目的。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	McGuckin N, Nakamoto Y. Trips, chains, and tours-using an operational definition[R]. Proceedings of National Household Travel Survey Conference Transportation, Washington D C, 2004: 1-15. [本文引用:1]
[2]	Prillwitz J, Barr S. Moving towards sustainability? Mobility styles, attitudes and individual travel behavior[J]. Journal of Transport Geography, 2011, 19(6): 1590-1600. [本文引用:1]
[3]	胡华, 滕靖, 高云峰, 等. 多模式公交信息服务条件下的出行方式选择行为研究[J]. 中国公路学报, 2009, 22(2): 87-92. Hu Hua, Teng Jing, Gao Yun-feng, et al. Research on travel mode choice behavior under integrated multi-modal transit information service[J]. China Journal of Highway and Transport, 2009, 22(2): 87-92. [本文引用:1]
[4]	Ben-Akiva M, Morikawa T. Estimation of switching models from revealed references and stated intentions[J]. Transportation Research Part A, 1990, 24(6): 485-495. [本文引用:3]
[5]	张峻屹, Fujiwara A, Soe T. 基于SP调查的缅甸仰光市居民收入对其出行方式选择的影响研究[J]. 交通运输系统工程与信息, 2008, 8(4): 49-62. Zhang Jun-yi, Fujiwara A, Soe T. Capturing travelers'stated mode choice preferences under the influence of income in yangon city, myanmar[J]. Journal of Transportation System Engineering and Information Technology, 2008, 8(4): 49-62. [本文引用:2]
[6]	Hensher D A, Bradley M. Using stated response data to enrich revealed preference discrete choice models[J]. Marketing Letters, 1993, 4(2): 139-152. [本文引用:2]
[7]	罗清玉, 孙宝凤, 吴文静, 等. 基于Mixed logit模型的拥挤收费下交通方式分担率预测[J]. 吉林大学学报: 工学版, 2010, 40(5): 1230-1234. Luo Qing-yu, Sun Bao-feng, Wu Wen-jing, et al. Predicting traffic mode split under congestion pricing based on mixed logit model[J]. Journal of Jilin University (Engineering and Technology Edition), 2010, 40(5): 1230-1234. [本文引用:1]
[8]	张天然, 杨东援, 赵娅丽, 等. RP/SP融合数据的Mixed Logit和Nested Logit模型估计对比[J]. 同济大学学报: 自然科学版, 2008, 36(8): 1073-1078. Zhang Tian-ran, Yang Dong-yuan, Zhao Ya-li, et al. Comparative study of RP/SP combined data estimation between mixed logit and nested logit[J]. Journal of Tongji University (Natural Science), 2008, 36(8): 1073-1078. [本文引用:3]
[9]	Börjesson M. Joint RP-SP data in a mixed logit analysis of trip timing decisions[J]. Transportation Research Part E, 2008, 44(6): 1025-1038. [本文引用:2]
[10]	Hensher D, Rose J, Greene W. Combining RP and SP data: biases in using the nested logit ‘trick’-contrasts with flexible mixed logit incorporating panel and scale effects[J]. Journal of Transport Geography, 2008, 16(2): 126-133. [本文引用:3]
[11]	郑柯, 郑勇. 基于极值分布的离散选择模型尺度参数[J]. 交通运输工程学报, 2009, 9(1): 92-95. Zheng Ke, Zheng Yong. Scale parameter of discrete choice model based on extreme value distribution[J]. Journal of Traffic and Transportation Engineering, 2009, 9(1): 92-95. [本文引用:1]
[12]	周伟, 赵胜川. 基于Mixed Logit模型的路线选择行为量化分析[J]. 吉林大学学报: 工学版, 2013, 43(2): 304-309. Zhou Wei, Zhao Sheng-chuan. Quantitative analysis of traveler route choice behavior based on Mixed Logit model[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(2): 304-309. [本文引用:1]
[13]	Bhat C R, Castelar S. A unified mixed logit framework for modeling revealed and stated preferences: formulation and application to congestion pricing analysis in San Francisco Bay area[J]. Transportation Research Part B, 2002, 36(7): 593-616. [本文引用:1]
[14]	Mcfadden D, Train K. Mixed MNL models for discrete response[J]. Journal of Applied Econometrics, 2000, 15(5): 447-470. [本文引用:1]
[15]	赵丹, 邵春福, 孙壮志, 等. 基于RP/SP融合数据的市郊铁路出行行为分析模型[J]. 交通运输系统工程与信息, 2010, 10(6): 156-162. Zhao Dan, Shao Chun-fu, Sun Zhuang-zhi, et al. Travel behavior analysis model of suburban railway based on combination of RP and SP data[J]. Journal of Transportation System Engineering and Information Technology, 2010, 10(6): 156-162. [本文引用:1]
[16]	Brownstone D, Bunch D, Train K. Joint mixed logit models of stated and revealed preferences for alternative-fuel vehicles[J]. Transportation Research Part B, 2000, 34(5): 315-338. [本文引用:1]
[17]	王劲峰, 姜成晟, 李连发. 空间抽样与统计推断[M]. 北京: 科学出版社, 2009. [本文引用:1]
[18]	关宏志. 非集计模型-交通行为分析的工具[M]. 北京: 人民交通出版社, 2004. [本文引用:1]

2004

0.0

... 0 引言通勤出行链(Commute trip chain)是指通勤者以工作单位为停驻点,从家出发再返回家的活动和出行组合^[1] ...

2011

0.0

... 目前大多数文献的研究对象均为单次出行的交通方式选择^[2,3,4],没有延伸到出行链范畴,割裂了出行间的相互联系 ...

2009

0.0

. 2009, 22(2):87-92 DOI:doi:10.1016/S1874-8651(10)60059-2

Research on travel mode choice behavior under integrated multi-modal transit information service

多模式公交信息服务条件下的出行方式选择行为研究

Hu Hua , Teng Jing , Gao Yun-feng

胡华, 滕靖, 高云峰

In order to scientifically evaluate the influences of integrated multi-modal transit information service (IMTIS) on travel mode choice behaviors, authors firstly analyzed its influence mechanism based on traffic hyper-network theory from the point of view of trip chain. Secondly, a nested Logit choice model was developed and travel time reliability factor was introduced to adjust the value of vital attribute variables of the utility function. Lastly, the nested Logit model was calibrated by maximum likelihood method based on data from a revealed preference survey conducted in the suburb of Shanghai, and usages of various travel modes with and without IMTIS were respectively counted out and contrasted. The result shows that IMTIS is effective to shift part travels from private modes to transit modes and thus improves share ratios of transit. Outcomes of this research can provide decision support for the development and improvement of transit information system in big cities.

为了科学评价多模式公交信息服务对出行方式选择行为的影响,基于超级交通网络理论,从出行链的角度分析了多模式公交信息服务对出行方式选择的影响机理,并在构建巢式Logit出行方式划分模型的基础上引入行程时间可靠度因子改进效用函数;根据上海市某郊区得到的显性偏好调查数据,利用极大似然法对巢式Logit模型进行参数标定后,对有无多模式公交信息服务条件下的出行方式分担率进行了计算和对比分析。研究结果表明:多模式公交信息服务能够有效引导轿车及其他个体机动化出行方式向多模式公交系统转移,提高了公交出行比例。研究结果可为大城市公共交通信息系统的改善和建设提供决策支持。

... 目前大多数文献的研究对象均为单次出行的交通方式选择^[2,3,4],没有延伸到出行链范畴,割裂了出行间的相互联系 ...

1990

0.0

... 目前大多数文献的研究对象均为单次出行的交通方式选择^[2,3,4],没有延伸到出行链范畴,割裂了出行间的相互联系 ...

... 在RP数据中融入SP数据,不仅能够消除单独使用SP数据产生的偏差,也增强了模型对出行环境变化下出行者潜在选择行为的预测和解释能力^[4,8],尤其是两种数据反映出的选择行为受到同一变量的影响近似相同时,优势更加明显^[9,10] ...

... 早期的研究多使用MNL模型建立RP-SP融合数据模型,其中一些文献直接忽略尺度系数差异^[4,5],还有一些通过改变SP数据的尺度以保证某些关键变量的系数与RP数据接近,然后将新的SP数据和RP数据融合进行参数估计^[14,15],但MNL模型完全不能解释异质性效应,且存在IIA(Independent from irrelevant alternative)特性 ...

2008

0.0

. 2008, 8(4):49-62

Capturing travelers'stated mode choice preferences under the influence of income in yangon city, myanmar

基于SP调查的缅甸仰光市居民收入对其出行方式选择的影响研究

Zhang Jun-yi , Fujiwara A , Soe T.

张峻屹

对于缅甸的仰光市而言,鉴于其新的快速轨道交通系统对于缓解城市现在以及将来的交通压力方面的作用,本文将依据SP调查数据对其居民出行方式选择行为进行研究.与发达国家相比,由于发展中国家诸如收入等社会经济环境因素变化相对较快,这就要求我们无论在调查方法还是模型构造上都要反映出这种交通行为决定因素的影响.因此,此次SP调查首先在设计上就反映出了将来的收入以及其他服务水平属性变化的影响;同时,也相应地进行了RP调查.接下来,要对一个RP/SP相结合的交通方式选择模型进行标定;在这个模型中,出行时间和费用的参数被分别定义为将来收入的函数.此次SP(以及RP)调查选在仰光市的一个住宅区进行,时间是2003年3 月.调查结果显示,与其他交通方式相比较,被调查的人对新的快速轨道交通系统显示出了极大的偏爱.利用调查上来的数据,本文对所提出的模型结构的有效性进行了验证.另外,模型对将来的模拟分析结果显示:随着收入的增加,将来仰光市小汽车的使用将有一个很大的增加,而新的快速轨道交通系统的利用将因此减少.

... RP-SP融合数据本身的特性对模型有一定要求,大量文献忽略了这些特性,仅采用多项logit(Multi-nominal logit,MNL)^[5]模型、巢式logit(Nested logit,NL)^[6]模型和一般mixed logit模型^[7]直接应用融合数据,降低了模型的解释能力和精度 ...

1993

0.0

... Hensher和Bradley^[6]利用NL模型解决了尺度系数差异的问题,但其不能有效地解释SP数据集中重复观测同一对象时,数据间可能存在的相关性,也不能考虑个体异质性 ...

2010

0.0

. 2010, 40(5):1230-1234

Predicting traffic mode split under congestion pricing based on mixed logit model

基于Mixed logit模型的拥挤收费下交通方式分担率预测

Luo Qing-yu , Sun Bao-feng , Wu Wen-jing

罗清玉, 孙宝凤, 吴文静

摘　要：分析了传统非集计模型存在的缺陷,提出利用mixed logit模型研究拥挤收费下交通方式分担率变化的思路。结合实际居民出行数据建立了基于mixed logit的交通方式选择模型,利用SAS软件进行蒙特卡罗模拟计算,标定了模型并进行了仿真分析。经验证,所建模型具有较高的命中率和可用性。加入拥挤收费影响因素进行敏感性分析,可得出不同拥挤收费费率下的交通方式分担率。应用该模型能为拥挤收费下的出行行为分析和交通影响研究以及其他交通需求管理政策的评价提供了方法。

2008

0.0

. 2008, 36(8):1073-1078 DOI:doi:10.3321/j.issn:0253-374X.2008.08.012

Comparative study of RP/SP combined data estimation between mixed logit and nested logit

RP/SP融合数据的Mixed Logit和Nested Logit模型估计对比

Zhang Tian-ran , Yang Dong-yuan , Zhao Ya-li

张天然, 杨东援, 赵娅丽

摘　要：分析了RP／SP（revealed preference／stated preference）融合数据对交通行为研究的重要性，通过实际调查的RP／SP融合数据，对比了用Mixed Logit和Nested Logit模型的估计结果．得出了以下结论：RP／SP融合数据中，有时同类型交通方式的关联性要比RP和SP数据之间的关联性强，应用不同的 Nested Logit模型分层方法进行估计对比；Mixed Logit考虑了个体的异质性，假定参数为随机分布，同时体现了RP／SP数据的关联性和同类型交通方式的关联性，能够得到更好的参数估计结果；Mixed Logit模型能更现实地反映不同交通方式使用者对时间和费用敏感性的不同（时间价值的不同），体现小汽车使用者比公共交通使用者具有更高时间价值的现实情况．

... 非显化异质性效应存在于RP和SP调查的各个环节,很多假设出行者具有共同偏好的模型被证实精度低于考虑异质性的模型^[8,10,12] ...

... 随后,mixed logit模型在RP-SP融合数据领域得到了广泛应用^[8,9,10] ...

2008

0.0

... 随后,mixed logit模型在RP-SP融合数据领域得到了广泛应用^[8,9,10] ...

2008

0.0

... 非显化异质性效应存在于RP和SP调查的各个环节,很多假设出行者具有共同偏好的模型被证实精度低于考虑异质性的模型^[8,10,12] ...

... 随后,mixed logit模型在RP-SP融合数据领域得到了广泛应用^[8,9,10] ...

2009

0.0

. 2009, 9(1):92-95

Scale parameter of discrete choice model based on extreme value distribution

基于极值分布的离散选择模型尺度参数

Zheng Ke , Zheng Yong.

郑柯, 郑勇

为了准确把握尺度参数在模型建模、分析以及应用过程中的作用,以基于极值分布的Multinomial Logit模型和Nested Logit模型为研究对象,从建模的基础——误差项的分布形式入手,通过模型形式和误差项性质两方面研究了尺度参数在两种模型中的特性,并对其进行了对比分析。分析结果表明:尺度参数不仅限制了模型效用函数的尺度,而且也反映了误差项的方差水平,但对于以上两种不同的模型,其在尺度限制、误差项方差水平及独立性、自身取值范围等方面均表现出不同的特性,Multinomial Logit模型的尺度参数反映了有关整个效用确定项的误差项方差水平,而Nested Logit模型的尺度参数只是反映了与某一选择枝有关的部分效用确定项的误差项方差水平。

... 尺度系数来源于误差项的分布,与误差项的方差成反比^[11] ...

2013

0.0

. 2013, 43(2):304-309

Quantitative analysis of traveler route choice behavior based on Mixed Logit model

基于Mixed Logit模型的路线选择行为量化分析

Zhou Wei , Zhao Sheng-chuan.

周伟, 赵胜川

To explore the effect of the urban road traffic dynamics on the traveler route choice behavior, a stated preference survey questionnaire was designed using the orthogonal design method. The survey was conducted with the travelers with driving experience in Dalian city. With the time parameter and the cost parameter fixed as well as the cost parameter obeying the normal distribution and lognormal distribution, a Logit model and a Mixed Logit model were built for the route choice analysis, and a quantitative analysis was performed for the route change trend caused by variables. The model estimation results indicated that the maximum likelihood, the values of goodness-of-fit index, and hit ratio of the Mixed Logit model are better than those of the Logit model. The traveler sensitivity for the travel time and dynamic change of time information are similar, and the most sensitive parameter is the travel cost. The traveler age, years of driving experience and income are the most significant factors affecting the route choice behavior.

为了探讨路况信息动态变化对出行路线选择行为的影响程度,采用正交试验法设计出行意愿调查问卷,针对有驾车经验的出行者进行调查。假定时间参数和费用参数为常数、费用参数服从正态分布和对数正态分布,分别建立了出行路线选择的Logit模型和Mixed Logit模型,并对解释变量影响路线改变倾向进行了量化分析。结果表明,Mixed Logit模型的最大似然值、优度比和命中率都高于Logit模型。出行者对行程时间和时间信息动态变化的敏感程度十分接近,敏感度最高的是出行费用。个人属性中的年龄、驾龄和收入是影响路线选择行为的最显著因素。

... 非显化异质性效应存在于RP和SP调查的各个环节,很多假设出行者具有共同偏好的模型被证实精度低于考虑异质性的模型^[8,10,12] ...

2002

0.0

... 并且,数据集中被访者的选择行为惯性的程度也不完全相同,建模时还要考虑参照依赖效应的异质性^[13] ...

2000

0.0

2010

0.0

2000

0.0

... 基于上述研究,Brownstone^[16]利用假设待估参数为随机分布的mixed logit模型使RP数据和SP数据得到了更好的融合,不仅避免了IIA特性,也突破了非显化异质性限制问题 ...

2009

0.0

... Latin超立方序列抽样法(Modified latin hypercube sampling,MLHS)采用分层技术,可以有效降低随机序列相关性,估计样本的均值和方差时对样本数量的节省也非常显著^[17] ...

2004

0.0

... 2,模型精度即达到标准^[18] ...