面板数据模型分析及交通事故预测

引用本文

孙璐, 徐建, 崔相民. 面板数据模型分析及交通事故预测. 2015, 45(6): 1771-1778
SUN Lu, XU Jian, CUI Xiang-min. Panel data models for analysis and prediction of crash count. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1771-1778 复制到剪切板

Permissions

面板数据模型分析及交通事故预测

孙璐^1,², 徐建^1,³, 崔相民⁴

1.东南大学交通学院,南京 210096

2.美国天主教大学土木工程系,华盛顿 20064

3.美国德克萨斯州大学奥斯汀分校交通研究中心,奥斯汀78712

4.山东省公路检测中心,山东济宁 272000

作者简介:孙璐(1972-),男,教授,博士生导师.研究方向:交通工程,道路工程.E-mail:sunl@cua.edu

基金:国家自然科学基金重点项目(U1134206); 国家自然科学基金外青学者项目(51250110075); 国家道路安全科技行动计划项目(2009BAG13A02); 交通运输部西部项目(0901005C); 美国国家科学基金总统奖项目(CMMI-0408390); 美国国家科学基金项目(CMMI-0644552)

摘要

构建了一种基于面板数据的空间非集计模型——负二项面板模型,包括混合效应、固定效应和随机效应3种类型,以同性质路段为研究单元,选取道路线形、交通特性、土地利用和降雨量等影响因素,利用事故率比例指标IRR,分析和预测未受伤事故、受伤事故、死亡事故和事故总数等4种类型事故,并通过F检验和Hausman检验以及对数似然值和离差信息准则DIC,对比分析3种类型模型的拟合效果。发现协变量对各类型交通事故的影响作用和统计显著性不尽相同,如限速每增加1.609 km/h(1 mile/h),未受伤事故、受伤事故、事故总数分别减少3.89%、2.24%和2.79%,而死亡事故增加6.38%。研究结果表明:负二项面板固定效应模型比混合模型和随机效应模型更优,另外越严重的事故,模型拟合效果越好。

关键词: 交通运输安全工程; 负二项面板模型; 固定效应模型; 土地利用; 降雨量

中图分类号:U491.31 文献标志码:A 文章编号:1671-5497(2015)06-1771-08

Panel data models for analysis and prediction of crash count

SUN Lu^1,², XU Jian^1,³, CUI Xiang-min⁴

1.School of Transportation, Southeast University, Nanjing 210096, China

2.Department of Civil Engineering, Catholic University of America, Washington DC 20064, USA

3.Center for Transportation Research, University of Texas at Austin, Austin 78712, USA

4.Shandong Provincial Highway Detection Center, Jining 272000, China

Abstract

Spatially disaggregated panel data models using negative binomial process, including pooled model, fixed-effects model and random-effect model, were developed. The contributing factors, such as roadway geometrics, traffic characteristics, land usage and rainfall were collected. Incidence Rate Ratio (IRR) and homogeneous segments were employed for analysis and prediction of crash count, which contains Property-Damage-Only (PDO) crashes, injury crashes, fatal crashes, and total crashes. Meanwhile, F test and Hausman test, log-likelihood value and Deviance Information Criterion (DIC) were used to compare the performance of the three types of models. It is found that the effects and statistical significance of covariates on the four types of crashes are not the same. For example, if the speed limit is increased by 1.609 km/h, the PDO rate, injury crash rate and total crash rate are reduced by 3.89%, 2.24% and 2.79%, respectively; however, the fatal crash rate is increased by 6.38%. Results show that the fixed-effects panel negative binomial model surpasses the pooled model and random-effect model, and the modeling is even better for crash count associated with more severe injuries and fatalities.

Keyword: traffic and transportation safety engineering; panel negative binomial model; fixed-effects model; land use; rainfall

Show Figures

0 引言

交通事故分析是为了研究交通事故总体分布情况、发展趋势以及影响因素对事故的作用和相互关系, 从宏观上定量地认识事故的本质和内在规律性, 能够为道路线形设计、安全改善措施、政策法规制定等提供重要依据。国内外学者对交通事故进行了大量研究, 国内学者主要对交通事故数据进行统计描述, 利用统计指标对道路进行安全性评价或事故预测^{[1, 2, 3]}。而国外学者的研究工作相对广泛而深入, 关于研究单元, 有城市层面^[4]、县域层面^[5]、人口普查区层面^[6]、路段层面^[7]等; 关于影响因素, 主要集中于道路线形和交通特性对交通事故的影响, 如选取路宽、分隔带宽度、平纵线形、限速、年平均日交通量(AADT)、车辆行驶里程(VMT)、设计小时交通量等因素^{[8, 9]}; 关于模型, 有负二项模型^[10]、对数正态模型^[11]、混合回归模型^[12]、零膨胀模型^[13]、空间模型^[14]等。

从国内外的研究工作可知:①目前研究多集中于截面数据, 即对某一定时期内交通事故数据分析, 而较少考虑事故的时间相关性, 较少研究面板数据^{[15, 16, 17]}; ②目前研究多集中于事故黑点、特殊路段等, 影响因素多选取道路线形和交通特性等, 而对土地利用、自然环境、气候等因素研究较少; ③目前研究多选取区域水平的研究单元, 而根据Openshaw在1984年提出的修正面积单元问题(MAUP)^[18], 不同的单元层面, 有不同的统计推断和解释, 区域水平的研究单元往往存在异质性问题, 导致研究存在不足。

针对目前研究工作的不足, 本文构建一种基于面板数据的空间非集计模型— — 负二项面板模型, 包括混合效应、固定效应和随机效应3种类型, 以同性质路段(指路段上几何线形与交通特性等指标一致)为研究单元, 选取道路线形、交通特性、土地利用和降雨量等10种影响因素, 以美国德克萨斯州奥斯汀市2007~2011年交通事故为研究数据, 分析并预测未受伤事故、受伤事故、死亡事故和事故总数等4种类型交通事故, 同时对比混合效应模型、固定效应模型与随机效应模型的拟合优良性。

1 基于面板数据的模型构建

本文构建负二项面板模型研究交通事故, 为了便于分析, 首先分别介绍标准泊松模型和负二项模型, 其次引入泊松面板模型, 最后建立负二项面板模型。泊松模型是最早应用于交通事故研究的回归模型, 它的形式为:

$\begin{matrix} P (Y = y_{i}) = \frac{λ_{i}^{y_{i}} e^{- λ_{i}}}{y_{i}!} (1) \end{matrix}$

式中:Y为随机变量, 表示交通事故起数(本文共有4种类型:未受伤事故起数、受伤事故起数、死亡事故起数和事故总起数); y_i为Y的具体观察值, i=1, 2, 3, …, n, 即共有n条路段单元。

泊松模型具有等散布性, 即均值与方差相等, E(Y)=Var(Y)=λ _i。交通事故起数与协变量(即交通事故影响因素)之间的关系为:

$\begin{matrix} \begin{matrix} λ_{i} = E (Y) = E (y_{i} |x_{ik}) = \\ \exp (\sum_{k} x_{ik} β_{k}) = \exp (x'_{i} β) (2) \end{matrix} \end{matrix}$

式中:β _k为第k个协变量的系数; β 为系数向量; x_ik为对应于第i条路段的第k个协变量; x_i为协变量向量。

由于泊松模型响应变量的均值和方差相等, 而实际交通事故的方差往往大于均值, 所以该模型有较大的局限性。在泊松模型的基础上, 负二项模型由于不受这样的约束, 而得到广泛的应用。负二项模型的均值方程包含随机变量ε _i, 并服从伽马分布, 即ε _i~Gamma(θ , θ ), 其表达式为:

$\begin{matrix} \begin{matrix} P (Y = y_{i}) = \\ \frac{Γ (y_{i} + 1 / ρ)}{Γ (y_{i} + 1) Γ (1 / ρ)} {(\frac{ρ λ_{i}}{1 + ρ λ_{i}})}^{y_{i}} {(\frac{1}{1 + ρ λ_{i}})}^{1 / ρ} (3) \end{matrix} \end{matrix}$

式中:ρ 为过度散布系数, 表示变量的散布程度, ρ =1/θ , 当ρ =0时, 负二项模型变为泊松模型。

面板数据模型通常有3种形式:①混合估计模型(Pooled regression model):从时间上和截面上均不存在显著性差异, 那么即可直接把面板数据混合在一起用普通最小二乘法(OLS)估计参数; ②固定效应模型(Fixed effects regression model):对于不同截面或不同时间序列, 模型的截距不同, 则常采用在模型中添加虚拟变量的方法估计回归参数, 即为固定效应模型; ③随机效应模型(Random effects regression model):如果固定效应模型的截距项包括截面随机误差项和时间随机误差项的平均效应, 并且这两个随机误差项都服从正态分布, 则成为随机效应模型。对于面板数据模型的选择, 通常采用F检验决定选用混合模型还是固定效应模型, 然后用Hausman检验确定建立随机效应模型还是固定效应模型。泊松面板随机效应模型的条件联合分布为:

$\begin{matrix} \begin{matrix} \Pr (y_{i 1}, \dots, y_{i T_{i}}) = \\ (\overset{T_{i}}{\prod_{t = 1}} \frac{λ_{it}^{y_{it}}}{y_{it}!}) \exp (- α_{i} \overset{T_{i}}{\sum_{t = 1}} λ_{it}) {α_{i}}^{\sum_{t}^{=} y_{it}} (4) \end{matrix} \end{matrix}$

式中:参数α _i~gamma(θ , θ ), 均值E(α _i)=1, 方差Var(α _i)=1/θ ; α _i为路段i的随机效应; T_i为面板数据的时间单元数(本文选取的交通事故数据为2007~2011年, 即T_i=5)。

将伽马分布α _i积分后, 式(4)变为非条件分布, 表达式为:

$\begin{matrix} \begin{matrix} \Pr (y_{i 1}, \dots, y_{i T_{i}} |x_{i}) = (\overset{T_{i}}{\prod_{t = 1}} \frac{λ_{it}^{y_{it}}}{y_{it}!}) \frac{Γ (θ + \sum_{t}^{=} y_{it})}{Γ (θ)} \\ (\frac{θ}{θ + \sum_{t}^{=} λ_{it}}) {(\frac{1}{θ + \sum_{t}^{=} λ_{it}})}^{\sum_{t}^{=} y_{it}} (5) \end{matrix} \end{matrix}$

对于泊松面板混合效应模型, 由于将面板数据合并后估计参数, 因此表达式为:

$\begin{matrix} \ln (λ_{i}) = \sum_{k} x_{ik} β_{k} + \sum_{i} α_{i} = x'_{i} β + α (6) \end{matrix}$

式中:α 为路段效应总和。

而对于泊松面板固定效应模型, 路段效应α _i可取任何值。若在交通事故总数 $\begin{matrix} \sum_{t}^{=} \end{matrix}$ y_it条件概率下, 固定效应值将从对数似然方程中消失, 这样系数β 即可被估计。那么, 基于交通事故总数 $\begin{matrix} \sum_{t}^{=} \end{matrix}$ y_it条件概率的路段概率表达式为:

$\begin{matrix} \begin{matrix} \Pr (y_{i 1}, \dots, y_{i T_{i}} |\sum_{t}^{=} y_{it}, x_{i}) = \\ \frac{(\sum_{t}^{=} y_{it})!}{\prod_{t}^{=} y_{it}!} \cdot \overset{T_{i}}{\prod_{t = 1}} {(\frac{λ_{it}}{\sum_{s}^{=} λ_{is}})}^{y_{it}} (7) \end{matrix} \end{matrix}$

前面分别介绍了标准泊松模型、负二项模型和泊松面板模型, 下面建立负二项面板模型。负二项面板分析中, 个体效应不应用于平均事故率, 而应用于分散度参数分布。当路段上分散度随机变化时, 随机效应模型是最合适的, 这类似于线性或连续的面板事件:个体效应在线性随机效应模型中随机分布, 而在线性固定效应模型中取任何值^[17]。在标准随机效应事件中, 根据贝塔分布(参数为ϕ 和φ ), 分散度在各路段上随机变化, 而伽马分布是一种特殊的贝塔分布, 能很好地拟合随机效应负二项模型, 表达式为:

$\begin{matrix} \begin{matrix} Y_{it} |γ_{it} ~Poisson (γ_{it}) (8) \\ γ_{it} |δ_{i} ~gamma (λ_{it}, 1 / δ_{i}) (9) \end{matrix} \end{matrix}$

式中:λ _it=exp(x'_itβ ); δ _i为分散度参数。

更广义的随机效应负二项模型中, 分散度参数是随机变化的, 1/(1+δ _i)~beta(φ , φ )。由此可得, 路段i的联合分布为:

$\begin{matrix} \begin{matrix} \Pr (y_{i 1}, \dots, y_{i T_{i}}) = \overset{T_{i}}{\prod_{t = 1}} \frac{Γ (λ_{it} + y_{it})}{Γ (λ_{it}) Γ (y_{it} + 1)} \times \\ \frac{Γ (ϕ + φ) Γ (ϕ + \sum_{t}^{=} λ_{it}) Γ (φ + \sum_{t}^{=} y_{it})}{Γ (ϕ) Γ (φ) Γ (ϕ + φ + \sum_{t}^{=} λ_{it} + \sum_{t}^{=} y_{it})} \\ (10) \end{matrix} \end{matrix}$

与泊松面板混合效应模型类似, 负二项面板混合效应模型表达式与式(6)一致。而对于负二项固定效应模型, 同样与泊松面板模型类似, 路段上的分散度参数可取任意值。Hausman等学者研究发现^[19], 当采用条件似然估计方法时, 分散度参数将消失, 而系数β 可被估计, 不必处理所有的固定效应参数。类似于泊松面板模型, 基于交通事故总数 $\begin{matrix} \sum_{t}^{=} \end{matrix}$ y_it的条件概率可表示为:

$\begin{matrix} \begin{matrix} \Pr (y_{i 1}, \dots, y_{i T_{i}} |\sum_{t}^{=} y_{it}) = \\ \frac{Γ (\sum_{t}^{=} λ_{it}) Γ (\sum_{t}^{=} y_{it} + 1)}{Γ (\sum_{t}^{=} λ_{it} + \sum_{t}^{=} y_{it})} \\ \overset{T_{i}}{\prod_{t = 1}} \frac{Γ (λ_{it} + y_{it})}{Γ (λ_{it}) Γ (y_{it} + 1)} (11) \end{matrix} \end{matrix}$

对于混合效应、固定效应和随机效应面板模型的选择问题, 可采用F检验和Hausman检验以及比较模型的对数似然值和拟合优度, 本文将在第3节研究结果分析中予以介绍。

2 研究数据概述

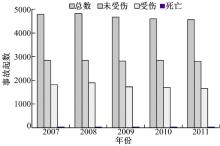
本文选取了美国德克萨斯州奥斯汀市2007~2011年交通事故资料作为研究数据。未受伤事故起数(仅财产损失事故PDO)、受伤事故起数、死亡事故起数和事故总起数等4种类型交通事故作为自变量, 图1为这4种类型事故随年份的分布数据图。从图1可知, 每年交通事故起数保持平稳, 变化较小, 但总体上呈微弱减少趋势。同时, 为了避免修正面积单元问题(MAUP), 将奥斯汀市的州级道路网(由德克萨斯州交通厅管理的路网)切割成1824条同性质路段作为研究单元, 平均路段长度为0.462 km(0.287 mile), 其中90%以上的路段集中于0~1 mile。

	Figure Option View Download New Window
	图1 奥斯汀市各类型事故的分布图Fig.1 Distributions of all types of crashes in Austin

然后, 利用ArcGIS软件将每年各类型交通事故与同性质路段合并, 即可得到每条路段上每年各类型交通事故起数。本文研究的协变量选取了车辆路段行驶距离(VMT)、平均路肩宽度、车道数、平曲线长度、平曲线度数、最大限速、卡车比例、降雨量、人口密度和就业密度等。其中道路线形与交通特性指标由德克萨斯州交通厅提供的RHiNo和GeoHiNi两大数据库通过计算获得, 其中RHiNo数据库包含了该州交通厅管理的所有道路的几何线形、标识符号、交通特性等一百多个指标, GeoHiNi数据库包含了所有道路中曲线路段的平纵横等几十个指标。降雨量与土地利用指标从美国国家统计局网站获取, 这两类指标都是基于人口普查区层面, 利用ArcGIS软件的线性参考功能将两类指标与相应的路段匹配。需说明的是, 奥斯汀市的土地利用资料无法获得, 由于土地利用类型包含商业用地、居住用地、农业用地、混合用地等, 而人口密度和就业密度在一定程度上能反映某区域的土地利用类型, 因此选取这两类密度指标替代土地利用类型。另外, 平均路肩宽度指外侧路肩和内侧路肩的平均值, 中央分隔带宽度不包含内侧路肩宽度, 平曲线度数指每一百英尺对应的曲线度数。交通事故对应的年份作为哑变量(是为1, 其他为0)应用于模型中, 其中2007年为参考变量, 2008~2011年为协变量。同性质路段的自变量与协变量的统计情况(均值、标准差、最小值和最大值)如表1所示。

表1 路段的自变量和协变量统计结果 Table 1 Summary statistics of dependent variables and covariates for segments

3 结果分析

本文运用3类负二项面板模型(混合效应、固定效应和随机效应)分析4种类型交通事故与影响因素的关系。选取了车辆路段行驶距离(VMT)、平均路肩宽度、车道数、平曲线长度、人口密度等多种协变量。近些年研究人员发现, 不同的协变量与交通事故存在不同的主次关系, 其中VMT、AADT(年平均日交通量)与路段长度等影响因素与交通事故起数存在主要关系, 一般情况下保持其他因素不变, VMT(或AADT、路段长度)与事故起数一一对应^[6]。因此, 为了提高模型拟合效果, 引入曝光变量。本文将VMT作为曝光变量, 如式(12)所示:

$\begin{matrix} λ_{i} = VM T_{i}^{α} \exp (\sum_{k} x_{ik} β_{k}) = VM T_{i}^{α} \exp (βx) (12) \end{matrix}$

式中:VMT_i表示第i条路段上车辆行驶总长度; α 为VMT的系数, 通常情况下曝光变量与事故起数一一对应, 根据Kweon和Kockelman的研究结果^[18], 当系数α =1时, 模型有最好的拟合优度和最好的预测效果。

为了全面比较负二项面板模型的三种效应模型, 本文引入F和Hausman两种检验以及对数似然值和离差信息准则(DIC)拟合优度。F检验是为了比较混合效应模型与固定效应模型, 零假设为H₀:各路段的效应都相等且为0, 检验表达式在文献[16]中查询。经计算, 未受伤事故的F值为2.38, 受伤事故的F值为2.44, 死亡事故的F值为6.07, 事故总数的F值为2.02, 均拒绝原假设。因此, 固定效应模型相对混合模型更适合本研究数据。

Hausman检验是为了比较固定效应模型与随机效应模型^[19], 其基本思路为:在α _i于其他协变量不相关的原假设下, 采用OLS估计固定效应模型和采用GLS估计随机效应模型得到的参数估计无偏且一致。若原假设不成立, 则固定效应模型的参数估计仍一致, 而随机效应模型不一致, Hausman检验表达式可在文献[19]中查询。经计算, 本文采用的4种类型交通事故的Hausman检验全部拒绝原假设, 说明随机效应模型估计不一致, 而固定效应模型更合适。

赤池信息准则(AIC)是衡量统计模型拟合优良性的一种标准, 表达式为AIC=2k-2ln(L), 其中, k为参数的数量, L为似然函数; 而离差信息准则(DIC)是基于贝叶斯理论并考虑了模型的复杂性, 它与赤池信息准则(AIC)意义相同, 其表达式为DIC=D $\begin{matrix} (\bar{θ}) \end{matrix}$ +2p_D= $\begin{matrix} \bar{D} \end{matrix}$ +p_D。其中, D $\begin{matrix} (\bar{θ}) \end{matrix}$ 为后验参数 $\begin{matrix} \bar{θ} \end{matrix}$ 的离差; p_D为模型中有效参数的数量; $\begin{matrix} \bar{D} \end{matrix}$ 为离差统计量D $\begin{matrix} (θ) \end{matrix}$ 的后验均值。DIC值越低, 说明模型拟合效果越好^[20]。对数似然值的计算公式为:

$\begin{matrix} \begin{matrix} LL = \overset{N}{\sum_{i = 1}} [nΓ (\frac{1}{α} + y_{i}) - \\ lnΓ (y_{i} + 1) - lnΓ (\frac{1}{α}) + \frac{1}{α} \ln (\frac{1}{1 + α λ_{i}}) + \\ y_{i} \ln (1 - \frac{1}{1 + α λ_{i}})] (13) \end{matrix} \end{matrix}$

经计算, 三种类型负二项面板模型的对数似然值和DIC如表2所示。

表2 三种类型负二项面板模型的对数似然值和DIC Table 2 Log likelihood and DIC for three types of panel negative binomial data models

从表2可知, 固定效应模型的对数似然值和DIC值在4种事故类型中均最小, 与F检验和Hausman检验的结果一致, 固定效应模型相对于混合模型和随机效应模型来说, 更加合适。值得注意的是, 从表2中发现, 大部分情况下, 随机效应模型的对数似然值和DIC值比混合模型小, 但在少数情况下, 结果却相反。另外, 4种类型事故中, 死亡事故的对数似然值和DIC值最小, 其次是受伤事故和未受伤事故, 而事故总数最大。这说明对于越严重的事故, 模型拟合效果越好, 该结论与Noland和Quddus两位学者的研究结果一致^[5]。

经过综合比较, 固定效应模型相对于混合效应模型和随机效应模型更合适, 因此本文以固定效应模型为主分析交通事故与影响因素之间的关系, 并作出相应的预测。负二项面板固定效应模型拟合结果如表3所示。对于未受伤事故, 平均路肩宽度、中央分隔带宽度、平曲线长度、最大限速、卡车比例、降雨量、人口密度和就业密度等协变量成统计显著性, 而其他协变量则不显著。车道数、平曲线度数、降雨量、人口密度等与事故起数成正相关, 而其他变量成负相关。另外, 年份哑变量对事故的影响作用亦不尽相同。如2008年和2010年与未受伤事故起数成正相关, 而其他则相反。对于受伤事故, 协变量统计显著性与未受伤事故不尽相同, 其中车道数和就业密度对于受伤事故呈显著性, 而对未受伤事故却不显著。对于两种类型事故协变量影响作用基本一致。对于死亡事故, 统计显著的协变量大为减少, 可能由于死亡事故起数较少, 即样本量偏少, 对统计结果产生一定的影响。值得注意的是, 最大限速在未受伤事故、受伤事故和事故总数中呈现正相关, 而在死亡事故中却相反, 呈现负相关, 即车道数越多, 死亡事故率越高。这可能由于车道数多的路段, 往往是高等级道路, 车流速度高, 一旦发生事故, 危险性高, 易产生死亡现象。而对于最大限速则完全相反, 即与在未受伤事故、受伤事故和事故总数中呈负相关, 而与死亡事故正相关, 这正好与车道数的潜在因素相对应。同时也说明, 并非限速越高事故越多, 因为限速高的路段线形往往更好, 同时驾驶员注意力更集中, 事故反而少。对于事故总数, 所有协变量均与事故成统计显著性, 且影响作用与未受伤事故和受伤事故基本一致。

表3 负二项面板固定效应模型的各类事故估计结果 Table 3 Estimation results of panel negative binomial fixed-effects model for kinds of crash counts

为了更好地描述协变量对各类型交通事故的现实意义, 本文引入事故率比例指标IRR(Incidence rate ratio)。为了保证事故率非负性, 对交通事故均值模型(如式(2)所示)进行了指数转换, 此时协变量系数影响作用与普通的线性模型不一样, 不能用简单的边际效应或平均弹性描述。本文采用IRR作为替代边际效应, 用于考察协变量对各类型交通事故的具体影响作用, 其表达式为:

$\begin{matrix} \begin{matrix} IRR (x_{j}) = \frac{\exp [β_{1} x_{1} + \dots + β_{j} (x_{j} + 1) + β_{J} x_{J}]}{\exp [β_{1} x_{1} + \dots + β_{j} x_{j} + β_{J} x_{J}]} \\ = \exp (β_{j}) (14) \end{matrix} \end{matrix}$

例如:如果β _j=-0.1, 则IRR(x_j)=exp(-0.1)=0.90, 这说明协变量x_j增加一个单位量, 平均事故率减少10%。经过计算, 各类型事故模型中协变量的IRR值如表4所示。

表4 协变量对各类型事故的影响作用 Table 4 Effect of covariates on all kinds of crashes

从表4可以清晰地看出, 每个协变量改变一个单位量时, 各类型交通事故率的变化情况。例如, 最大限速每增加1.609 km/h(1 mile/h), 未受伤事故起数减少3.89%; 受伤事故起数减少2.24%; 事故总起数减少2.79%; 死亡事故起数增加6.38%。其中人口密度和就业密度对于各类型事故影响最大, 这在一定程度上说明土地利用类型对交通事故产生重要影响。人口密度越大, 事故率越高, 而就业密度则完全相反。就业密度大的地方往往是商业用地, 而就业密度小的地方往往是农村地区(或农业用地), 该研究结果表明商业地区事故率低, 而农村地区事故率高, 这与Wang和Kockelman两位学者的研究结果一致^[6]。年份哑变量与其他连续型协变量不同, IRR值指年份从“ 不是” 变为“ 是” , 即0改变为1时的事故率变化。例如, 2008年相对于参考年份(2007年), 死亡事故率减少了15.6%。

4 结束语

通过F检验和Hausman检验, 以及对数似然值和离差信息准则, 说明负二项面板固定效应模型比混合效应模型和随机效应模型更优, 能较好地拟合面板数据。协变量对4种类型交通事故(未受伤事故、受伤事故、死亡事故和事故总数)的影响作用和统计显著性不尽相同, 其中事故总数的显著变量最多, 而死亡事故最少。同时研究发现越严重的交通事故, 面板数据模型拟合效果越好。事故率比例指标IRR表示协变量对事故的具体作用。另外, 人口密度和就业密度对于各类型事故影响最大, 这在一定程度上说明土地利用类型对交通事故产生重要影响。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	马壮林, 邵春福, 李霞. 基于Logistic模型的公路隧道交通事故严重程度的影响因素[J]. 吉林大学学报: 工学版, 2010, 40(2): 423-426. Ma Zhuang-lin, Shao Chun-fu, Li Xia. Analysis of factors affecting accident severity in highway tunnels based on logistic model[J]. Journal of Jilin University(Engineering and Technology Edition), 2010, 40(2): 423-426. [本文引用:1]
[2]	李铁洪, 吴华金. 长直线接小半径曲线公路交通事故成因及预防对策[J]. 中国公路学报, 2007, 20(1): 35-40. Li Tie-hong, Wu Hua-jin. Causes and countermeasures of highway traffic accidents in long straight line combined with sharp curve[J]. China Journal of Highway and Transport, 2007, 20(1): 35-40. [本文引用:1]
[3]	黄合来, 邓雪, 许鹏鹏. 考虑空间自相关的贝叶斯事故预测模型[J]. 同济大学学报: 自然科学版, 2013, 41(9): 1378-1383. Huang He-lai, Deng Xue, Xu Peng-peng. Bayesian crash prediction model based on a consideration of spatial autocorrelation[J]. Journal of Tongji University (Natural Science), 2013, 41(9): 1378-1383. [本文引用:1]
[4]	Jones A P, Haynes R, Kennedy V, et al. Geographical variations in mortality and morbidity from road traffic accidents in England and Wales[J]. Health & Place, 2008, 14(3): 519-535. [本文引用:1]
[5]	Noland R B, Quddus M A. A spatially disaggregate analysis of road casualties in England [J]. Accident Analysis & Prevention, 2004, 36(6): 973-984. [本文引用:2]
[6]	Wang Y, Kockelman K M. A conditional-autoregressive count model for pedestrian crashes across neighborhoods[R]. The 92nd Annual Meeting of the Transportation Research Board, 2013. [本文引用:3]
[7]	Ma J M, Kockelman K M, Boothe C. Bayesian multivariate Poisson regression for models of injury count, by severity[J]. Transportation Research Record, 2006, 1950(1): 24-34. [本文引用:1]
[8]	Abdel-Aty M, Radwan A E. Modeling traffic accident occurrence and involvement[J]. Accident Analysis & Prevention, 2000, 32(5): 633-642. [本文引用:1]
[9]	Wang C, Quddus M A, Ison S G. Predicting accident frequency at their severity levels and its application in site ranking using a two-stage mixed multivariate model[J]. Accident Analysis & Prevention, 2011, 43(6): 1979-1990. [本文引用:1]
[10]	Ma J M, Kockelman K M, Damien P. A multivariate Poisson-lognormal regression model for prediction of crash counts by severity, using Bayesian methods[J]. Accident Analysis & Prevention, 2008, 40(3): 964-975. [本文引用:1]
[11]	Lord D. The prediction of accidents on digital networks: characteristics and issues related to the application of accident prediction models[D]. Toronto: University of Toronto, 2000. [本文引用:1]
[12]	Park B J, Lord D. Application of finite mixture models for vehicle crash data analysis[J]. Accident Analysis & Prevention, 2009, 41(4): 683-691. [本文引用:1]
[13]	Lambert D. Zero-inflated Poisson regression with an application to defects in manufacturing[J]. Technometrics, 1992, 34(1): 1-14. [本文引用:1]
[14]	Qin X, Reyes P. Conditional quantile analysis for crash count data[J]. Journal of Transportation Engineering, 2011, 137(9): 601-607. [本文引用:1]
[15]	王军雷, 孙小端, 贺玉龙, 等. 交通事故宏观计量经济学模型[J]. 交通运输工程学报, 2012, 12(2): 70-75. Wang Jun-lei, Sun Xiao-duan, He Yu-long, et al. Macroscopic econometrics model of traffic accident[J]. Journal of Traffic and Transportation Engineering, 2012, 12(2): 70-75. [本文引用:1]
[16]	徐婷, 孙小端, 王伟力, 等. 基于Panel Data的高速公路事故预测模型[J]. 北京工业大学学报, 2010, 36(4): 495-499. Xu Ting, Sun Xiao-duan, Wang wei-li, et al. Highway accidents statistical analysis with panel data model[J]. Journal of Beijing University of Technology, 2010, 36(4): 495-499. [本文引用:1]
[17]	Kweon Y J, Kockelman K M. Spatially disaggregate panel models of crash and injury counts: the effect of speed limits and design[R]. Transportation Research Board 83rd Annual Meeting, 2004. [本文引用:2]
[18]	Openshaw S. The modifiable areal unit problem[J]. Concepts and Techniques in Modern Geography, 1984. [本文引用:2]
[19]	Hausman J, Hall B, Griliches Z. Econometric models for count data with an application to the patents-R&D relationship[J]. Econometrica, 1984, 52(4): 909-938. [本文引用:2]
[20]	Oh J, Lyon C, Washington S P, et al. Validation of the FHWA crash models for rural intersections: lessons learned[J]. Transportation Research Record, 2003, 1840: 41-49. [本文引用:1]

2010

0.0

. 2010, 40(2):423-426

Analysis of factors affecting accident severity in highway tunnels based on logistic model

基于Logistic模型的公路隧道交通事故严重程度的影响因素

Ma Zhuang-lin , Shao Chun-fu , Li Xia.

马壮林, 邵春福, 李霞

School of Traffic &|Transportation|Beijing Jiaotong University|Beijing 100044|China

Based on the traffic accident data collected from the 4 tunnels in Shaoguan section of Beijingzhuhai freeway, taking the accident severity as dependent variable, selecting 9 candidate independent variables from 3 aspects: the time of the accident happened, the tunnel environment, and the traffic dynamic factors, the relevance between the candidate independent variables and the dependent variable was analyzed by the reverse selection method. It was found that the time of the accident happened, the collision type, the weather condition, and the ratio of daily PCU to AADT are the factors that most significantly related to the accident severity. The effects of these most related factors on the accident severity was analyzed using a logistic regression model. A statistical interpretation was given to the modeled estimates in terms of the odds ratio concept. The proposed logistic regression model was tested on the goodnessoffit and predictive accuracy and the encouraging result was achieved.

根据京珠高速公路韶关段4个隧道的交通事故资料，以事故严重程度为因变量，从时间、隧道环境和交通动态因素3个方面选择9个候选自变量，采用反向选择法分析候选自变量与因变量是否显著相关。研究发现：事故发生时段、碰撞类型、天气和日标准小客车交通量与年平均日交通量（AADT）之比与事故严重程度显著相关。采用logistic回归模型，分析了事故发生时段、碰撞类型、天气和日标准小客车交通量与AADT之比对交通事故严重程度的影响程度，并根据发生比率的概念，对模型的估计情况进行了解释。最后，从模型的拟合优度和预测准确度2个方面对模型进行检验。结果表明，建立的logistic回归模型在事故严重程度影响因素分析中具有较好的适应性和实用性。

... 国内外学者对交通事故进行了大量研究,国内学者主要对交通事故数据进行统计描述,利用统计指标对道路进行安全性评价或事故预测^[1,2,3] ...

2007

0.0

. 2007, 20(1):35-40

Causes and countermeasures of highway traffic accidents in long straight line combined with sharp curve

长直线接小半径曲线公路交通事故成因及预防对策

Li Tie-hong , Wu Hua-jin.

李铁洪, 吴华金

1. Highway Planning, Survey and Design Institute of Yunnan Province, Kunming 650011, Yunnan, China; 2. Transportation Consultation Ltd of Yunnan Province, Kunming 650031, Yunnan, China

The traffic accident causes were analyzed and the problems in current standard were pointed out based on the research on the types of accidents in sharp curve. In addition, corresponding countermeasures were put forward by cases analysis of the traffic accidents in long straight line combined with sharp curve. The result indicates that although the accident in long straight combined with sharp curve is inevitable, it follows certain rules and the rate of accidents in the kind of segment can be cut down by suitable measures.

根据小半径曲线路段的各种交通事故形态, 对事故的成因作了分析, 并指出现行相关规范的不足, 提出了长直线及小半径曲线的界定方法;结合长直线接小半径曲线路段交通事故的实例分析, 进一步提出了相应的预防措施。研究结果表明:长直线接小半径曲线路段交通事故的发生有其必然性和规律性, 通过适当的措施和手段, 可以大大减少这种路段上的交通事故。

... 国内外学者对交通事故进行了大量研究,国内学者主要对交通事故数据进行统计描述,利用统计指标对道路进行安全性评价或事故预测^[1,2,3] ...

2013

0.0

... 国内外学者对交通事故进行了大量研究,国内学者主要对交通事故数据进行统计描述,利用统计指标对道路进行安全性评价或事故预测^[1,2,3] ...

2008

0.0

... 而国外学者的研究工作相对广泛而深入,关于研究单元,有城市层面^[4]、县域层面^[5]、人口普查区层面^[6]、路段层面^[7]等 ...

2004

0.0

... 而国外学者的研究工作相对广泛而深入,关于研究单元,有城市层面^[4]、县域层面^[5]、人口普查区层面^[6]、路段层面^[7]等 ...

... 这说明对于越严重的事故,模型拟合效果越好,该结论与Noland和Quddus两位学者的研究结果一致^[5] ...

2013

0.0

... 而国外学者的研究工作相对广泛而深入,关于研究单元,有城市层面^[4]、县域层面^[5]、人口普查区层面^[6]、路段层面^[7]等 ...

... 近些年研究人员发现,不同的协变量与交通事故存在不同的主次关系,其中VMT、AADT(年平均日交通量)与路段长度等影响因素与交通事故起数存在主要关系,一般情况下保持其他因素不变,VMT(或AADT、路段长度)与事故起数一一对应^[6] ...

... 就业密度大的地方往往是商业用地,而就业密度小的地方往往是农村地区(或农业用地),该研究结果表明商业地区事故率低,而农村地区事故率高,这与Wang和Kockelman两位学者的研究结果一致^[6] ...

2006

0.0

... 而国外学者的研究工作相对广泛而深入,关于研究单元,有城市层面^[4]、县域层面^[5]、人口普查区层面^[6]、路段层面^[7]等 ...

2000

0.0

... 关于影响因素,主要集中于道路线形和交通特性对交通事故的影响,如选取路宽、分隔带宽度、平纵线形、限速、年平均日交通量(AADT)、车辆行驶里程(VMT)、设计小时交通量等因素^[8,9] ...

2011

0.0

2008

0.0