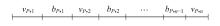基于分段思想的变截面连续梁桥动力特性计算

引用本文

刘寒冰, 时成林, 谭国金, 王华, 黄彬. 基于分段思想的变截面连续梁桥动力特性计算. 2015, 45(6): 1779-1783
LIU Han-bing, SHI Cheng-lin, TAN Guo-jin, WANG Hua, HUANG Bin. Calculation method of the dynamic characteristics of continuous beam bridge with variable cross-section based on staging concept. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1779-1783 复制到剪切板

Permissions

基于分段思想的变截面连续梁桥动力特性计算

刘寒冰¹, 时成林^1,², 谭国金¹, 王华¹, 黄彬¹

1.吉林大学交通学院,长春 130022

2.吉林省交通科学研究所科研开发中心,长春 130012

谭国金(1981-),男,副教授,博士.研究方向:桥梁检测与加固.E-mail:tgj@jlu.edu.cn

作者简介:刘寒冰(1957-),男,教授,博士生导师.研究方向:桥梁检测与加固.E-mail:lhb@jlu.edu.cn

基金:国家自然科学基金项目(51478203)

摘要

对连续梁桥的每一跨进行分段,采用待定系数表示每一段的振型函数,并且依据段间的连续条件建立每一跨内待定系数的传递方程。依据全部边界条件和传递方程,形成全桥待定系数的求解方程,通过对待定系数方程的求解便可计算出桥梁的自振频率和振型。最后,采用该方法对一座连续梁桥的动力特性进行求解,验证了该方法的有效性和可靠性。

关键词: 连续梁桥; 变截面; 动力特性; 分段算法

中图分类号:U441 文献标志码:A 文章编号:1671-5497(2015)06-1779-05

Calculation method of the dynamic characteristics of continuous beam bridge with variable cross-section based on staging concept

LIU Han-bing¹, SHI Cheng-lin^1,², TAN Guo-jin¹, WANG Hua¹, HUANG Bin¹

1.College of Transportation, Jilin University,Changchun 130022,China

2.Scientific Research and Development Center,Jilin Provincial Transport Scientific Research Institute, Changchun 130012, China

Abstract

A calculation method of the dynamic characteristics of continuous beam bridge with variable cross-section is proposed based staging concept. In this method, each cross of a girder bridge is segmented; the undetermined coefficients are used to express the vibration mode function of each segment; the transfer equations within the undetermined coefficients of each cross are established based on intersegmental continuity condition. The equations of the full-bridge undetermined coefficients are formed based on all the boundary conditions and transfer equations. The method is able to calculate the natural frequency and vibration mode of the bridge by solving the equations of undetermined coefficients. This method is applied to solve the dynamic characteristics of a continuous box girder bridge to demonstrate its validity and reliability.

Keyword: continuous beam bridge; variable cross-section; dynamic characteristics; segmentation algorithm

Show Figures

0 引言

近几十年来, 变截面梁式结构的动力特性求解方法研究已取得一些成果。Laura^[1]研究了高度沿梁长方向呈双线性变化、宽度不变的变截面矩形梁固有频率的求解方法。Naguleswaran^[2]给出了边长为梁长二次函数的变截面矩形梁自振频率的求解方法。Mao^{[3, 4]}借助于Adomian分解对阶梯梁的动力特性求解问题开展了研究。徐腾飞等^[5]研究了变化轴力作用下变截面简支梁动力特性的级数解析解。这些方法要求梁的截面按一定的规律变化, 能否应用到任意变化截面的求解中还有待进一步研究。

文献[6]基于模态摄动方法, 给出了变截面梁式结构动力特性的数值求解方法。李俊等^[7]采用动态传递矩阵对Timoshenko薄壁梁的动力特性进行了求解。楼梦麟等^[8]借助于模态摄动方法, 求解了Timoshenko简支梁的动力特性。把以上研究成果应用到变截面连续梁桥的动力特性求解中, 其计算过程都极其冗繁。

崔灿等^[9]采用分段思想, 给出了变截面简支梁动力特性的求解方法, 该方法对截面的变化规律没有任何限制, 并且求解过程简单。但该方法不能直接应用到变截面连续梁的动力特性求解中。本文以文献[9]为基础, 提出了一种求解变截面连续梁桥动力特性的方法, 该方法首先对连续梁进行分段, 通过段间的连续条件和连续梁的边界条件形成待定系数矩阵。最后通过待定系数矩阵特征方程的求解来实现动力特性的求解。该方法计算过程简单, 便于工程实现。

1 单跨内待定系数的传递

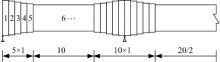
为了不失一般性, 设m跨连续梁的第p跨截面变化形式如图1所示, 其中共有n个截面变化段v_p_{, 1}, v_p_{, 2}, …, v_p_,_n; n-1个截面不变段b_p_{, 1}, b_p_{, 2}, …, b_p_,_n-₁。

	Figure Option View Download New Window
	图1 第p跨截面分布Fig.1 The p span section distribution

基于分段思想, 把v_p_,_i等间距地分解成Q小段, 每小段的长度为 $\begin{matrix} l_{v_{p, i}} \end{matrix}$ , 从左到右的编号分别为1, 2, …, Q。每一小段的惯性矩和线密度分别取该小段的平均值^[9], 则第j小段的惯性矩和线密度分别为:

$\begin{matrix} \{\begin{matrix} I_{v_{p, i}}^{j} = \frac{1}{l_{v_{p, i}}} \int_{0}^{l_{v_{p, i}}} I (x) dx, 0 \leq x \leq l_{v_{p, i}} \\ m_{v_{p, i}}^{j} = \frac{1}{l_{v_{p, i}}} \int_{0}^{l_{v_{p, i}}} m (x) dx, 0 \leq x \leq l_{v_{p, i}} \end{matrix} (1) \end{matrix}$

设v_p_,_i变化段中第j小段的振型函数为:

$\begin{matrix} \begin{matrix} φ_{v_{p, i}}^{j} (x) = A_{v_{p, i}}^{j} \sin β_{v_{p, i}}^{j} x + B_{v_{p, i}}^{j} \cos β_{v_{p, i}}^{j} x + \\ C_{v_{p, i}}^{j} \sinh β_{v_{p, i}}^{j} x + D_{v_{p, i}}^{j} \cosh β_{v_{p, i}}^{j} x, 0 \leq x \leq l_{v_{p, i}} (2) \end{matrix} \end{matrix}$

式中:( $\begin{matrix} β_{v_{p, i}}^{j} \end{matrix}$ )⁴=(ω ² $\begin{matrix} m_{v_{p, i}}^{j} \end{matrix}$ )/(E $\begin{matrix} I_{v_{p, i}}^{j} \end{matrix}$ ), ω 为整个连续梁的自振频率; $\begin{matrix} A_{v_{p, i}}^{j} \end{matrix}$ 、 $\begin{matrix} B_{v_{p, i}}^{j} \end{matrix}$ 、 $\begin{matrix} C_{v_{p, i}}^{j} \end{matrix}$ 、 $\begin{matrix} D_{v_{p, i}}^{j} \end{matrix}$ 为与第j小段对应的4个待定系数。

令 $\begin{matrix} \{S_{v_{p, i}}^{j}\} \end{matrix}$ = $\begin{matrix} [\begin{matrix} A_{v_{p, i}}^{j} & B_{v_{p, i}}^{j} & C_{v_{p, i}}^{j} & D_{v_{p, i}}^{j} \end{matrix}] \end{matrix}$ , $\begin{matrix} \{S_{v_{p, i}}^{j + 1}\} \end{matrix}$ = $\begin{matrix} [\begin{matrix} A_{v_{p, i}}^{j + 1} & B_{v_{p, i}}^{j + 1} & C_{v_{p, i}}^{j + 1} & D_{v_{p, i}}^{j + 1} \end{matrix}] \end{matrix}$ , 利用第j小段右端与第j+1小段左端位移、转角、弯矩和剪力连续的条件^[9], 可得:

$\begin{matrix} Z_{v_{p, i}}^{j + 1} \{S_{v_{p, i}}^{j + 1}\} = Z_{v_{p, i}}^{j} \{S_{v_{p, i}}^{j}\} (3) \end{matrix}$

式中: $\begin{matrix} Z_{v_{p, i}}^{j + 1} \end{matrix}$ , $\begin{matrix} Z_{v_{p, i}}^{j} \end{matrix}$ 的表达式分别为:

$\begin{matrix} Z_{v_{p, i}}^{j + 1} \end{matrix}$ = $\begin{matrix} [\begin{matrix} 0 & 1 & 0 & 1 \\ K & 0 & K & 0 \\ 0 & - K^{2} M & 0 & K^{2} M \\ - K^{3} M & 0 & K^{3} M & 0 \end{matrix}] \end{matrix}$ (4)

式中:K= $\begin{matrix} β_{v_{p, i}}^{j + 1} \end{matrix}$ ; M=E $\begin{matrix} l_{v_{p, i}}^{j + 1} \end{matrix}$ 。

$\begin{matrix} \begin{matrix} Z_{v_{p, i}}^{j} = \\ [\begin{matrix} s_{1} & s_{2} & s_{3} & s_{4} \\ K' s_{2} & - K' s_{1} & K' s_{4} & K' s_{3} \\ - M' {(K')}^{2} s_{1} & - M' {(K')}^{2} s_{2} & M' {(K')}^{2} s_{3} & M' {(K')}^{2} s_{4} \\ - M' {(K')}^{3} s_{2} & M' {(K')}^{3} s_{1} & M' {(K')}^{3} s_{4} & M' {(K')}^{3} s_{3} \end{matrix}] (5) \end{matrix} \end{matrix}$

式中:K'= $\begin{matrix} β_{v_{p, i}}^{j} \end{matrix}$ ; M'=E $\begin{matrix} I_{v_{p, i}}^{j} \end{matrix}$ ; s₁=sin $\begin{matrix} β_{v_{p, i}}^{j} \end{matrix} \begin{matrix} l_{v_{p, i}} \end{matrix}$ ; s₂=cos $\begin{matrix} β_{v_{p, i}}^{j} \end{matrix} \begin{matrix} l_{v_{p, i}} \end{matrix}$ ; s₃=sinh $\begin{matrix} β_{v_{p, i}}^{j} \end{matrix} \begin{matrix} l_{v_{p, i}} \end{matrix}$ ; s₄=cosh $\begin{matrix} β_{v_{p, i}}^{j} \end{matrix} \begin{matrix} l_{v_{p, i}} \end{matrix}$ 。由式(3)可得:

$\begin{matrix} \{S_{v_{p, i}}^{j + 1}\} = {[Z_{v_{p, i}}^{j + 1}]}^{- 1} Z_{v_{p, i}}^{j} \{S_{v_{p, i}}^{j}\} (6) \end{matrix}$

令 $\begin{matrix} T_{v_{p, i}}^{j} \end{matrix}$ = $\begin{matrix} {[Z_{v_{p, i}}^{j + 1}]}^{- 1} \end{matrix} \begin{matrix} Z_{v_{p, i}}^{j} \end{matrix}$ , 基于式(6)中待定系数的传递关系, 可以得到v_p_,_i变化段中第1小段和最后一小段(第Q小段)的待定系数传递关系为:

$\begin{matrix} \{S_{v_{p, i}}^{Q}\} = T_{v_{p, i}}^{Q - 1} \dots T_{v_{p, i}}^{2} T_{v_{p, i}}^{1} \{S_{v_{p, i}}^{1}\} (7) \end{matrix}$

令 $\begin{matrix} H_{v_{p, i}} \end{matrix}$ = $\begin{matrix} T_{v_{p, i}}^{Q - 1} \end{matrix}$ … $\begin{matrix} T_{v_{p, i}}^{2} \end{matrix} \begin{matrix} T_{v_{p, i}}^{1} \end{matrix}$ , 该矩阵表示v_p_,_i变化段中第一小段的待定系数与最后一小段待定系数的总体传递关系。则式(7)又可写成:

$\begin{matrix} \{S_{v_{p, i}}^{Q}\} = H_{v_{p, i}} \{S_{v_{p, i}}^{1}\} (8) \end{matrix}$

设紧邻v_p_,_i变化段右端的不变段b_p_,_i的待定系数向量{ $\begin{matrix} S_{b_{p, i}} \end{matrix}$ }=[ $\begin{matrix} \begin{matrix} A_{b_{p, i}} & B_{b_{p, i}} & C_{b_{p, i}} & D_{b_{p, i}} \end{matrix} \end{matrix}$ ]; 不变段b_p_,_i的长度为 $\begin{matrix} l_{b_{p, i}} \end{matrix}$ ; ( $\begin{matrix} β_{b_{p, i}} \end{matrix}$ )⁴=(ω ² $\begin{matrix} m_{b_{p, i}} \end{matrix}$ )/(E $\begin{matrix} I_{b_{p, i}} \end{matrix}$ ); 惯性矩为 $\begin{matrix} I_{b_{p, i}} \end{matrix}$ 。则v_p_,_i变化段中最后一小段(第Q小段)与不变段b_p_,_i的待定系数传递关系可用式(9)表示:

$\begin{matrix} \{S_{b_{p, i}}\} = {[R_{b_{p, i}}^{l}]}^{- 1} Z_{v_{p, i}}^{Q} \{S_{v_{p, i}}^{q}\} (9) \end{matrix}$

式中:矩阵 $\begin{matrix} R_{b_{p, i}}^{l} \end{matrix}$ 中的元素可通过把不变段b_p_,_i的参数代入式(4)而得到。

不变段b_p_,_i与v_p_,_i+₁变化段中第1小段的待定系数传递关系可表示为:

$\begin{matrix} \{S_{v_{p, i + 1}}^{1}\} = {[Z_{v_{p, i + 1}}^{1}]}^{- 1} {R^{r}}_{b_{p, i}} \{S_{b_{p, i}}\} (10) \end{matrix}$

式中:矩阵 $\begin{matrix} Z_{v_{p, i + 1}}^{1} \end{matrix}$ 中的元素可由v_p_,_i+₁变化段中第1小段的参数代入式(4)得到; 矩阵 $\begin{matrix} R_{b_{p, i}}^{r} \end{matrix}$ 中的元素由不变段b_p_,_i的参数代入式(5)得到。

综合式(8)(9)(10)可以得到待定系数在一个整跨内的传递关系, 例如本文中的第p跨左端第一小段(位于第p跨的左支点处)与第p跨右端最后一小段(位于第p跨的右支点处)待定系数的传递关系为:

$\begin{matrix} \begin{matrix} \{S_{v_{p, n}}^{Q}\} = H_{v_{p, n}} {[Z_{v_{p, n}}^{1}]}^{- 1} {R^{r}}_{b_{p, n - 1}} {[{R^{l}}_{b_{p, n - 1}}]}^{- 1} \times \\ Z_{v_{p, n - 1}}^{Q} \dots H_{v_{p, 2}} {[Z_{v_{p, 2}}^{1}]}^{- 1} {R^{r}}_{b_{p, 1}} {[{R^{l}}_{b_{p, 1}}]}^{- 1} \times \\ Z_{v_{p, 1}}^{Q} H_{v_{p, 1}} \{S_{v_{p, 1}}^{1}\} (11) \end{matrix} \end{matrix}$

令：

$Λ_{p} = H_{v_{p, n}} {[Z_{v_{p, n}}^{1}]}^{- 1} {R^{r}}_{b_{p, n - 1}} {[{R^{l}}_{b_{p, n - 1}}]}^{- 1} Z_{v_{p, n - 1}}^{Q} \dots$

$H_{v_{p, 2}} {[Z_{v_{p, 2}}^{1}]}^{- 1} {R^{r}}_{b_{p, 1}} {[{R^{l}}_{b_{p, 1}}]}^{- 1} Z_{v_{p, 1}}^{Q} H_{v_{p, 1}}$

则式(11)可简化为:

$\begin{matrix} \{S_{v_{p, n}}^{Q}\} = Λ_{p} \{S_{v_{p, 1}}^{1}\} (12) \end{matrix}$

式(12)为第p跨待定系数的整体传递关系。

2 边界条件及动力特性求解

2.1 边界条件

设第p+1跨的左端第1段为变化截面, 把该变化段等间距地分为若干小段, 每小段的长度为 $\begin{matrix} l_{v_{p + 1, 1}} \end{matrix}$ 。对于第p跨的右端支点, 竖向位移等于0, 则有:

$\begin{matrix} \begin{matrix} φ_{v_{p, n}}^{Q} (l_{v_{p, n}}) = 0 (13) \\ φ_{v_{p + 1, 1}}^{1} (0) = 0 (14) \end{matrix} \end{matrix}$

对于第p跨的右端支点, 同样满足转角和弯矩连续, 则有:

$\begin{matrix} \begin{matrix} φ'_{v_{p, n}}^{Q} (l_{v_{p, n}}) = φ'_{v_{p + 1, 1}}^{1} (0) (15) \\ E I_{v_{p, n}}^{Q} φ ″_{v_{p, n}}^{Q} (l_{v_{p, n}}) = E I_{v_{p + 1, 1}}^{1} φ ″_{v_{p + 1, 1}}^{1} (0) (16) \end{matrix} \end{matrix}$

把振型函数代入式(13)~(16)中, 则有:

$\begin{matrix} \begin{matrix} A_{v_{p, n}}^{Q} \sin β_{v_{p, n}}^{Q} l_{v_{p, n}} + B_{v_{p, n}}^{Q} \cos β_{v_{p, n}}^{Q} l_{v_{p, n}} + \\ C_{v_{p, n}}^{Q} \sinh β_{v_{p, n}}^{Q} l_{v_{p, n}} + D_{v_{p, n}}^{Q} \cosh β_{v_{p, n}}^{Q} l_{v_{p, n}} = 0 (17) \\ B_{v_{p + 1, 1}}^{1} + D_{v_{p + 1, 1}}^{1} = 0 (18) \\ β_{v_{p, n}}^{Q} (A_{v_{p, n}}^{Q} \cos β_{v_{p, n}}^{Q} l_{v_{p, n}} - B_{v_{p, n}}^{Q} \sin β_{v_{p, n}}^{Q} l_{v_{p, n}} + \\ C_{v_{p, n}}^{Q} \cosh β_{v_{p, n}}^{Q} l_{v_{p, n}} + D_{v_{p, n}}^{Q} \sinh β_{v_{p, n}}^{Q} l_{v_{p, n}}) - \\ β_{v_{p + 1, 1}}^{1} A_{v_{p + 1, 1}}^{1} - β_{v_{p + 1, 1}}^{1} C_{v_{p + 1, 1}}^{1} = 0 (19) \\ I_{v_{p, n}}^{Q} (β_{v_{p, n}}^{Q})^{2} (- A_{v_{p, n}}^{Q} \sin β_{v_{p, n}}^{Q} l_{v_{p, n}} - \\ B_{v_{p, n}}^{Q} \cos β_{v_{p, n}}^{Q} l_{v_{p, n}} + C_{v_{p, n}}^{Q} \sinh β_{v_{p, n}}^{Q} l_{v_{p, n}} + \\ D_{v_{p, n}}^{Q} \cosh β_{v_{p, n}}^{Q} l_{v_{p, n}}) + I_{v_{p + 1, 1}}^{1} (β_{v_{p + 1, 1}}^{1})^{2} B_{v_{p + 1, 1}}^{1} - \\ I_{v_{p + 1, 1}}^{1} (β_{v_{p + 1, 1}}^{1})^{2} D_{v_{p + 1, 1}}^{1} = 0 (20) \end{matrix} \end{matrix}$

把式(17)~(20)写成矩阵的形式, 则有:

$\begin{matrix} [G] \{S\} = [\begin{matrix} G_{p}^{r} & G_{p + 1}^{l} \end{matrix}] \{\begin{matrix} S_{v_{p, n}}^{Q} \\ S_{v_{p + 1, 1}}^{1} \end{matrix}\} = 0 (21) \end{matrix}$

式中: $\begin{matrix} \{S_{v_{p + 1, 1}}^{1}\} \end{matrix}$ = $\begin{matrix} {[\begin{matrix} A_{v_{p 1, 1}}^{1} & B_{v_{p 1, 1}}^{1} & C_{v_{p 1, 1}}^{1} & D_{v_{p 1, 1}}^{1} \end{matrix}]}^{T} \end{matrix}$ ; $\begin{matrix} [{G^{l}}_{p + 1}] \end{matrix}$ 、 $\begin{matrix} [{G^{r}}_{p}] \end{matrix}$ 的表达式为:

$\begin{matrix} \begin{matrix} [{G^{l}}_{p + 1}] = \\ [\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 \\ - β_{v_{p + 1, 1}}^{1} & 0 & - β_{v_{p + 1, 1}}^{1} & 0 \\ 0 & I_{v_{p + 1, 1}}^{1} {(β_{v_{p + 1, 1}}^{1})}^{2} & 0 & - I_{v_{p + 1, 1}}^{1} {(β_{v_{p + 1, 1}}^{1})}^{2} \end{matrix}] (22) \end{matrix} \end{matrix}$

$\begin{matrix} [{G^{r}}_{p}] = [\begin{matrix} \sin β_{v_{p, n}}^{Q} l_{v_{p, n}} & \cos β_{v_{p, n}}^{Q} l_{v_{p, n}} & \sinh β_{v_{p, n}}^{Q} l_{v_{p, n}} & \cosh β_{v_{p, n}}^{Q} l_{v_{p, n}} \\ 0 & 0 & 0 & 0 \\ β_{v_{p, n}}^{Q} \cos β_{v_{p, n}}^{Q} l_{v_{p, n}} & - β_{v_{p, n}}^{Q} \sin β_{v_{p, n}}^{Q} l_{v_{p, n}} & β_{v_{p, n}}^{Q} \cosh β_{v_{p, n}}^{Q} l_{v_{p, n}} & β_{v_{p, n}}^{Q} \sinh β_{v_{p, n}}^{Q} l_{v_{p, n}} \\ - I_{v_{p, n}}^{Q} {(β_{v_{p, n}}^{Q})}^{2} \sin β_{v_{p, n}}^{Q} l_{v_{p, n}} & - I_{v_{p, n}}^{Q} {(β_{v_{p, n}}^{Q})}^{2} \cos β_{v_{p, n}}^{Q} l_{v_{p, n}} & I_{v_{p, n}}^{Q} {(β_{v_{p, n}}^{Q})}^{2} \sinh β_{v_{p, n}}^{Q} l_{v_{p, n}} & I_{v_{p, n}}^{Q} {(β_{v_{p, n}}^{Q})}^{2} \cosh β_{v_{p, n}}^{Q} l_{v_{p, n}} \end{matrix}] (23) \end{matrix}$

连续梁桥要求最左端和最右端满足位移和弯矩等于0的边界条件。m跨连续梁满足最左端的边界条件, 可得:

$\begin{matrix} \begin{matrix} [{G^{l}}_{1}] \{{S^{l}}_{1}\} = 0 (24) \end{matrix} \end{matrix}$

式中：

$[{G^{l}}_{1}] = [\begin{matrix} 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & - 1 \end{matrix}];$

$\{{S^{l}}_{1}\} = [\begin{matrix} A_{v_{1, 1}}^{1} & B_{v_{1, 1}}^{1} & C_{v_{1, 1}}^{1} & D_{v_{1, 1}}^{1} \end{matrix}] 。$

m跨连续梁满足最右端的边界条件, 可得:

$\begin{matrix} [{G^{r}}_{m}] \{{S^{r}}_{m}\} = 0 (25) \end{matrix}$

式中:{ $\begin{matrix} {S^{r}}_{m} \end{matrix}$ }= $\begin{matrix} [\begin{matrix} A_{v_{m, n}}^{Q} & B_{v_{m, n}}^{Q} & C_{v_{m, n}}^{Q} & D_{v_{m, n}}^{Q} \end{matrix}] \end{matrix}$ ; $\begin{matrix} [{G^{r}}_{m}] \end{matrix}$ 的表达式为:

$\begin{matrix} [{G^{r}}_{m}] = {[\begin{matrix} \sin β_{v_{m, n}}^{Q} l_{v_{m, n}} & - \sin β_{v_{m, n}}^{Q} l_{v_{m, n}} \\ \cos β_{v_{m, n}}^{Q} l_{v_{m, n}} & - \cos β_{v_{m, n}}^{Q} l_{v_{m, n}} \\ \sinh β_{v_{m, n}}^{Q} l_{v_{m, n}} & \sinh β_{v_{m, n}}^{Q} l_{v_{m, n}} \\ \cosh β_{v_{m, n}}^{Q} l_{v_{m, n}} & \cosh β_{v_{m, n}}^{Q} l_{v_{m, n}} \end{matrix}]}^{T} (26) \end{matrix}$

2.2 动力特性求解

把式(12)代入式(21)中, 可得:

$\begin{matrix} [\begin{matrix} {G^{r}}_{p} Λ_{p} & {G^{l}}_{p + 1} \end{matrix}] \{\begin{matrix} S_{v_{p, 1}}^{1} \\ S_{v_{p + 1, 1}}^{1} \end{matrix}\} = 0 (27) \end{matrix}$

把式(12)代入式(25)中, 同样可得:

$\begin{matrix} [{G^{r}}_{m}] [Λ_{m}] \{S_{v_{m, 1}}^{1}\} = 0 (28) \end{matrix}$

式中:{ $\begin{matrix} S_{v_{m, 1}}^{1} \end{matrix}$ }为第m跨最左端变化段第1小段的待定系数矩阵。

对于m跨连续梁桥, 利用式(24)(27)(28), 把所有边界条件综合成矩阵的形式, 则有:

$\begin{matrix} [G] \{R\} = 0 (29) \end{matrix}$

式中:{R}=[ $\begin{matrix} A_{v_{1, 1}}^{1} \end{matrix}$ $\begin{matrix} B_{v_{1, 1}}^{1} \end{matrix}$ $\begin{matrix} C_{v_{1, 1}}^{1} \end{matrix}$ $\begin{matrix} D_{v_{1, 1}}^{1} \end{matrix}$ … $\begin{matrix} A_{v_{p, 1}}^{1} \end{matrix}$ $\begin{matrix} B_{v_{p, 1}}^{1} \end{matrix}$ $\begin{matrix} C_{v_{p, 1}}^{1} \end{matrix}$ $\begin{matrix} D_{v_{p, 1}}^{1} \end{matrix}$ … $\begin{matrix} A_{v_{m, 1}}^{1} \end{matrix}$ $\begin{matrix} B_{v_{m, 1}}^{1} \end{matrix}$ $\begin{matrix} C_{v_{m, 1}}^{1} \end{matrix} \begin{matrix} D_{v_{m, 1}}^{1} \end{matrix}$ ]; $\begin{matrix} [G] \end{matrix}$ 为一个4m行、4m列的矩阵, 其表达式为:

$\begin{matrix} \begin{matrix} [G] = \\ [\begin{matrix} {G^{l}}_{1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ {G^{r}}_{1} Λ_{1} & {G^{l}}_{2} & 0 & 0 & 0 & 0 & 0 & 0 \\ ⋱ \\ 0 & 0 & 0 & {G^{r}}_{p} Λ_{p} & {G^{l}}_{p + 1} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {G^{r}}_{p + 1} & {G^{l}}_{p + 2} & 0 & 0 \\ ⋱ \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {G^{r}}_{m} Λ_{m} \end{matrix}] (30) \end{matrix} \end{matrix}$

在 $\begin{matrix} \{R\} \end{matrix}$ 中的元素不全为0的情况下, 使得式(29)成立, 则必须满足:

$\begin{matrix} |G| = 0 (31) \end{matrix}$

当矩阵 $\begin{matrix} [G] \end{matrix}$ 维数较高时, 可以采用迭代算法对式(31)进行求解, 通过对式(31)的求解可以得到m跨连续梁桥的4m阶自振频率。并且可以得到与第i阶自振频率对应的特征向量{R_i}。综合利用式(12)、振型函数以及特征向量{R_i}, 便可以求解出连续梁桥的第i阶振型。值得一提的是本文在推导过程中假定了每跨的第1段和最后1段为变截面, 如果为截面不变的情况, 采用本文的方法同样可以进行求解, 即本文的方法可以满足截面变化任意分布的情况。

3 计算结果及比较

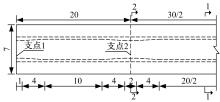
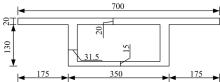
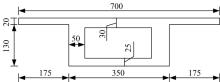
为了验证本文方法的正确性和可靠性, 以图2所示的3跨连续梁桥(另一半对称结构在图2中未体现)为数值模拟对象。桥梁跨径组成为:20 m+30 m+20 m, 跨中截面和支点截面分别如图3和图4所示, 腹板和底板厚度在同一段变化, 变化长度均为4 m。全桥采用C50混凝土, 弹性模量E=3.45× 10¹⁰ Pa, 容重ρ =2.5× 10⁴ N/m³。

	Figure Option View Download New Window
	图2 连续梁平面图(单位:m)Fig.2 Plan of continuous beam(unit:m)

	Figure Option View Download New Window
	图3 1-1跨中截面(单位:cm)Fig.3 Mid-span(unit:cm)

	Figure Option View Download New Window
	图4 2-2支点截面(单位:cm)Fig.4 Fulcrum section of 2-2(unit:cm)

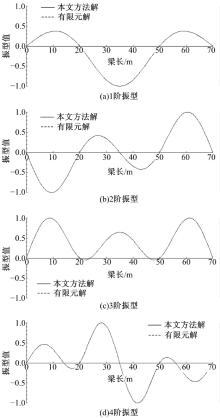
将连续梁桥的每个截面变化段分成4小段, 不变段作为一段, 连续梁桥截面划分如图5所示。采用本文方法计算了该桥的动力特性, 由于篇幅限制, 在此只给出前4阶计算结果。前4阶自振频率列于表1中, 前4阶振型如图6所示。

	Figure Option View Download New Window
	图5 连续梁分段示意图(单位:m)Fig.5 Segmental diagram of continuous beam(unit:m)

表1 自振频率计算结果 Table 1 Results of natural frequency(unit:Hz)

	Figure Option View Download New Window
	图6 连续梁桥前4阶振型Fig.6 First four vibration modal shape of continuous beam

由计算结果可知, 本文方法与有限元方法得出的计算结果十分接近, 这说明本文方法精度较高, 可以可靠地应用于变截面连续梁桥动力特性的求解。

4 结束语

基于分段思想, 采用振型函数表示每段的振动, 并得到了振型函数中待定系数在每跨内的传递关系, 结合边界条件, 形成了变截面连续梁桥的动力特性求解方法。把此方法应用到了一座3跨连续箱梁桥的动力特性计算中, 计算结果表明本文方法具有较高的精度。该方法计算过程简单, 并且不要求连续梁桥的截面服从任何变化规律。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Laura P A A, Gutierrez R H, Rossi R E. Free vibration of beams of bilinearly varying thickness[J]. Ocean Engineering, 1996, 23(1): 1-6. [本文引用:1]
[2]	Naguleswaran S. Vibration in the two principal pla-nes of a non-uniform beam of rectangular cross-section one side of which varies as the square root of the axial coordinate[J]. Journal of Sound and Vibration, 1994, 172(3): 305-319. [本文引用:1]
[3]	Mao Q B. Free vibration analysis of multiple-stepped beams by using adomian decomposition method[J]. Mathematical and Computer Modeling, 2011, 54(1-2): 756-764. [本文引用:1]
[4]	Mao Q B, Pietrzko S. Free vibration analysis of stepped beams by using adomian decomposition method[J]. Applied Mathematics and Computation, 2010, 217(7): 3429-3441. [本文引用:1]
[5]	徐腾飞, 向天宇, 赵人达. 变截面Euler-Bernoulli梁在轴力作用下固有振动的级数解[J]. 振动与冲击, 2007, 26(11): 99-101, 186. Xu Teng-fei, Xiang Tian-yu, Zhao Ren-da. Series solution of natural vibration of the variable cross-section euler-bernoulli beam under axial force[J]. Journal of Vibration and Shock, 2007, 26(11): 99-101, 186. [本文引用:1]
[6]	张怀静, 潘旦光. 变截面连续梁动力特性的半解析解法[J]. 北京科技大学学报, 2008, 30(6): 590-593, 619. Zhang Huai-jing, Pan Dan-guang. Semi-analytic solution to dynamic characteristics of non-uniform continuous beams[J]. Journal of University of Science and Technology Beijing, 2008, 30(6): 590-593, 619. [本文引用:1]
[7]	李俊, 金咸定. Timoshenko 薄壁梁弯扭耦合振动的动态传递矩阵法[J]. 振动与冲击, 2001, 20(4): 57-59, 61. Li Jun, Jin Xian-ding. Dynamic transfer matrix method for bending-torsional vibration of timoshenko thin-walled beam[J]. Journal of Vibration and Shock, 2001, 20(4): 57-59, 61. [本文引用:1]
[8]	楼梦麟, 任志刚. Timoshenko简支梁的振动模态特性精确解[J]. 同济大学学报, 2002, 30(8): 911-915. Lou Meng-lin, Ren Zhi-gang. Precise solution to modal characteristics of Timoshenko pin-ended beams[J]. Journal of Tongji University(Natural Science), 2002, 30(8): 911-915. [本文引用:1]
[9]	崔灿, 蒋晗, 李映辉. 变截面梁横向振动特性半解析法[J]. 振动与冲击, 2012, 31(14): 85-88. Cui Can, Jiang Han, Li Ying-hui. Semi-analytical method for calculating vibration characteristics of variable cross-section beam[J]. Journal of Vibration and Shock, 2012, 31(14): 85-88. [本文引用:3]

1996

0.0

... Laura^[1]研究了高度沿梁长方向呈双线性变化、宽度不变的变截面矩形梁固有频率的求解方法 ...

1994

0.0

... Naguleswaran^[2]给出了边长为梁长二次函数的变截面矩形梁自振频率的求解方法 ...

2011

0.0

... Mao^[3,4]借助于Adomian分解对阶梯梁的动力特性求解问题开展了研究 ...

2010

0.0

... Mao^[3,4]借助于Adomian分解对阶梯梁的动力特性求解问题开展了研究 ...

2007

0.0

... 徐腾飞等^[5]研究了变化轴力作用下变截面简支梁动力特性的级数解析解 ...

2008

0.0

2001

0.0

... 李俊等^[7]采用动态传递矩阵对Timoshenko薄壁梁的动力特性进行了求解 ...

2002

0.0

... 楼梦麟等^[8]借助于模态摄动方法,求解了Timoshenko简支梁的动力特性 ...

2012

0.0

. 2012, 31(14):85-88

Semi-analytical method for calculating vibration characteristics of variable cross-section beam

变截面梁横向振动特性半解析法

Cui Can , Jiang Han , Li Ying-hui.

崔灿, 蒋晗, 李映辉

School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China

Abstract: A semi-analytical approach for bending vibration of variable cross-section beam is developed in this research. The variable cross-section beam model allowed parameters, such as bending stiffness and mass per unit, to vary in a manner of continuous and non-continuous which are related to axial coordinate. Based on Euler-Bernoulli beam theory, the transverse oscillation equation of variable cross-section beam is derived. Then, the beam is modeled a number of segments connected by continuity condition, and each segment of the continuous beam is assumed to obey characteristic of uniform cross section. The relation of modal functions of contiguous segments is derived by using the conditions for continuity of displacement, slope of deflection curve, moment, and shear force at the connecting point between contiguous segments. Furthermore, the modal functions are determined for simply supported boundary conditions, and the natural frequencies can be obtained using Newton-Raphson method. To verify the effect of this method, the first five natural frequencies and modal shape of beam are presented. Results show that the natural frequencies of variable cross-section beam approximately encouraging agreement those numerically obtained by the finite-element method.

摘要：提出了一种计算变截面梁横向振动特性的半解析法。基于欧拉-伯努利梁理论给出的弯曲刚度、质量分布沿梁轴线连续或非连续变化的变截面梁横向振动方程；将该变截面梁等效为多段均匀梁，并基于相邻两段连接处的位移(位移、转角)和力(弯矩、剪力)的连续条件，建立了两相邻均匀段之间模态函数的关系；针对简支边界条件给出了计算变截面梁横向振动固有频率的特征方程和模态函数，并用Newton-Raphson方法计算其固有频率。通过与有限元法的数值结果比较说明了本文半解析解的高精度和有效性。

... 崔灿等^[9]采用分段思想,给出了变截面简支梁动力特性的求解方法,该方法对截面的变化规律没有任何限制,并且求解过程简单 ...

... 每一小段的惯性矩和线密度分别取该小段的平均值^[9],则第j小段的惯性矩和线密度分别为: ...

... 令 Svp,ij=Avp,ijBvp,ijCvp,ijDvp,ij, Svp,ij+1=Avp,ij+1Bvp,ij+1Cvp,ij+1Dvp,ij+1,利用第j小段右端与第j+1小段左端位移、转角、弯矩和剪力连续的条件^[9],可得: ...